1 Introduction

Tomographic PIV (Elsinga et al. 2006) is nowadays a widespread measurement technique for the measurement of the 3D instantaneous velocity and vorticity field in fluid flows. Also, the advent of high-speed CMOS cameras and diode-pumped lasers has made it possible to operate PIV systems in the kilohertz range (Hain et al. 2007). Despite these developments, the number of reported tomographic PIV experiments conducted in the time-resolved regime is still rather small for air flows (Scarano 2013). This is mostly due to the trade-off between laser pulse energy and extent of the illuminated volume, which is particularly critical for tomographic experiments. As a result, most time-resolved tomographic PIV experiments conducted at repetition rates of 10 kHz or higher in air flows deal with a very small measurement volume (e.g. Ghaemi et al, 2012; Pröbsting et al. 2013). It is clear that, to date, the achievable measurement rate for time-resolved 3D tomographic PIV remains insufficient for aerodynamic problems where the flow velocity may approach 100 m/s. Methods that increase the measurement rate are therefore of great interest and relevance.

In a recent study (Scarano and Moore 2011), the idea of post-processing measured velocity fields with a physics-based numerical solver in order to recover unmeasured time slices (time-supersampling) was investigated. An advection-only approximation of the Navier–Stokes equations was used based on the hypothesis of frozen turbulence. A significant increase in temporal resolution and anti-aliasing behaviour was demonstrated in the turbulent wake past an airfoil. However, the application to free shear layers failed as a result of the flow model inadequacy to the vortex-dominated regime.

The present work generalizes Scarano and Moore (2011) by using a vortex-in-cell (VIC) inviscid, incompressible Navier–Stokes solver (Christiansen 1973; Cottet and Koumoutsakos 2000), to perform time-supersampling of 3D velocity time series obtained from tomographic PIV experiments. The expectation is that, by using a more complete flow model, a method of more general validity is obtained.

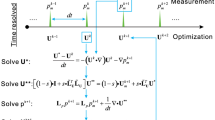
The approach is based on the accurate numerical solution of the unsteady Navier–Stokes equations. The VIC method is applied on the measurement domain, using velocity data from a given measurement as the initial condition. The assumption of inviscid flow makes integration backwards in time possible. The latter holds valid provided that the contribution of viscous terms is negligible with respect to the inertia. When a measured time series is available, this allows temporal continuity of the solution to be imposed, by performing a weighted average of forward and backward integration. Figure 1 illustrates schematically the principle of time-supersampling.

Fig. 1
figure 1

The time-supersampling principle. Top increasing time series resolution by combined forward–backward integration between snapshots. Bottom temporal data reconstruction from an isolated velocity field snapshot. Right diagrams representing the velocity temporal evolution and its reconstruction

Full size image

Related investigations have dealt with the problem of filling spatial gaps in PIV data using an incompressible finite volume Navier–Stokes solver (Sciacchitano et al. 2012), preceded by a study of Suzuki et al. (2009a, b) who combined planar PTV with large eddy simulation around an airfoil. The specific use of the vorticity transport equation with particle discretization has already been proposed by Cuzol and Mémin (2009) for temporal tracking of velocity fields from image sequences (e.g. satellite imagery) demonstrating the potential of the approach, at least for large-scale flow structures in the two-dimensional regime. The problem of temporal reconstruction has also been tackled using standard interpolation techniques. However, the general outcome is that this approach is not able to reconstruct past the Nyquist limit. For example, a proper orthogonal decomposition (POD) based method proposed by Druault et al. (2005) has successfully reconstructed the large-scale dynamical evolution of a tumbling vortex inside an internal combustion engine. Such reconstructions are however possible only within the hypothesis of flow quasi-periodicity and are only valid for the large-scale structures of the flow (Bouhoubeiny and Druault 2009).

The method presented herein is restricted to application to 3D measurement data from incompressible flow experiments. As shown in Fig. 1, the VIC method can be applied to both time-resolved data as well as to single instantaneous measurements, which implies four main potential applications of VIC to 3D PIV data:

  1. 1.

    Time-supersampling

  2. 2.

    Reducing measurement noise of time-resolved data

  3. 3.

    Computation of instantaneous pressure field from a single 3D velocity field (as opposed to high-speed or 4-pulse systems)

  4. 4.

    Bandlimited spectral estimates from low repetition rate PIV measurements

Despite relevance of the above points, the present work concentrates only on the first one and the study of VIC for the possible applications from points 2 to 4 are left outside the scope of this investigation. In particular, point 3 is of great potential interest: by extracting the instantaneous velocity material derivative and in turn the pressure gradient field, spatial integration yields the instantaneous unsteady pressure field. This may represent a much simpler alternative to high-speed PIV measurements (see the review from Oudheusden et al. 2007) or dual-time PIV systems for planar (Liu and Katz 2006) and tomographic experiments (Lynch and Scarano 2013).

The paper briefly introduces the VIC method and its numerical implementation, before detailing the implementation for experimental datasets. Subsequently, two cases are considered: the first one is the fully developed turbulent flow in the near wake past the trailing edge of a NACA-0012 airfoil (Ghaemi and Scarano 2011); the second case is a transitional jet in water with large-scale coherent vortices developing along the free shear layer (Violato and Scarano 2011). The assessment methodology follows that of Scarano and Moore (2011) where originally time-resolved datasets are used, which are first under-sampled by some factor, then resampled by the time-supersampling technique and finally compared with the measured data series. The method is also compared to a point-wise linear interpolation and the advection model, which only accounts for linear transport of flow properties. A quantitative analysis of the reconstruction accuracy is based on the Euclidean norm of the discrepancy between the reconstructed values and the measured ones. An additional discussion takes into account the bias of such estimator in presence of a significant measurement noise level.

2 Vortex-in-cell method

The accuracy of time-supersampling depends upon the accuracy of the model used to reconstruct the flow between the measured time samples. The incompressible Navier–Stokes equations represent a highly accurate approximation for the flows we wish to supersample. Furthermore, using a numerical discretization based on the vorticity formulation ensures good reproduction and preservation of vortical features in the flow at low computational cost. This is ideal for reconstructing unsteady flows, in particular turbulence.

The VIC technique was introduced by Christiansen (1973) and solves the inviscid, incompressible Navier–Stokes equations in the form of the vorticity transport equation,

$$\frac{\partial {\varvec{\omega}}}{\partial{t}} + \left(\varvec{u}\cdot\varvec{\nabla}\right) \varvec{\omega}=\left({\varvec{\omega}\cdot \varvec{\nabla}}\right)\varvec{u},$$
(1)

where the vorticity field \({\varvec{\omega}}\) is discretized by N Lagrangian vortex particles on a Cartesian grid (Fig. 2) at locations \({\varvec{x}}^p=\{{\varvec{x}}_1^p, \dots, {\varvec{x}}_N^p\}\) with particle strengths \({\varvec{\alpha}}^p=\{{\varvec{\alpha}}_1^p,\dots, {\varvec{\alpha}}_N^p\}\). The vorticity vector at location \({\varvec{x}}=[x,y,z]^T\) follows from a summation over all vortex particles,

$$\varvec{\omega}(\varvec{x},{t}) = \sum_{i=1}^N {\varvec \alpha}^p_i\delta\left[{\varvec{x}- \varvec{x}{^p_i(t)}}\right],$$
(2)

with δ the 3D Dirac delta function. In 2D, the particle strength represents circulation around the vortex particle and is by analogy named the circulation strength vector in 3D.

Fig. 2
figure 2

Particle advection, where particles are moved from their initial location (white) to their updated location at time \(t_1+\Updelta t\) (black); the arrows represent the velocity vectors at each particle location at t = t 1

Full size image

The behaviour of the vortex particles is governed, in an inviscid flow, by two ordinary differential equations. One for particle advection,

$$\frac{d {\varvec{x}{^p_i}}}{d {t}} = \varvec{u} (\varvec{x}{_i^p},t),$$
(3)

and a second one to update particle strength, accounting for vortex stretching,

$$\frac{d {\varvec{\alpha}{_i^p}}}{d {t}}=\varvec{\alpha}{_i^p} \cdot \varvec{\nabla} \varvec{u}(\varvec{x}{_i^p},t).$$
(4)

The vorticity vector field is related to the velocity field by a Poisson equation (see for example Koumoutsakos 2005),

$$\nabla^2 \varvec{u} = -\varvec{\nabla} \times {\varvec{\omega}}.$$
(5)

These equations are solved numerically (Sect. 3) using initial conditions on vorticity computed from PIV measurement data (Fig. 1). Given that experimental data are affected by small measurement errors, and the model is imperfect, the solution obtained by integrating forward from time T 1 until \(T_2 = T_1+\Updelta T\) does not match exactly the measured sample at T 2. To obtain temporal continuity, the reconstructed velocity field \({\varvec{u}}\) is calculated as a weighted average of the solutions from a single forward integration \({\varvec{u}}_f\) and a single backward integration \({\varvec{u}}_b\),

$$\varvec{u}(\varvec{x},{t}) = \frac{t-T_1}{\Updelta T} \varvec{u}_b(\varvec{x},{t}) + \frac{T_2-t}{\Updelta T}\varvec{u}_f(\varvec{x},{t})$$
(6)

Backward time integration can only be considered a consistent approach if the effects of viscous diffusion are neglected to make the vorticity transport equation time-reversible. This introduces an additional approximation in the numerical model of the flow. A detailed theoretical discussion of the conditions under which this error remains negligible goes beyond the scope of the present study. However, in the remainder, an error analysis is given from which one can infer that the hypothesis of negligible viscous effects holds valid when dealing with turbulent flows measured here. In many applications relevant for aerodynamics, the turbulent flow regime is characterized by a dynamical evolution that is dominated by convection and partly by sole advection. Examples are given by Oudheusden et al. (2007) and Ghaemi et al. (2012).

The proposed method is only applicable where the VIC approximation of Navier–Stokes is a good model for the flow. 2D (planar) PIV measurements seldom deal with 2D flow fully described within the measurement plane, which certainly will not be the case of turbulence. The 2D Navier–Stokes equations are therefore an incomplete model for the in-plane flow. A typical side effect of 2D measurements is that the velocity field will not be divergence-free. To date, no application of the VIC method to planar data from 3D flows appears possible within the limits of the current approach; hence, the present study only considers the case of 3D measurement data obtained via tomographic PIV.

3 Numerical treatment

For a detailed description of the VIC method, the reader is referred to the available literature, in particular Cottet and Koumoutsakos (2000) and references therein. In this section, the numerical treatment of the equations will be explained, focusing on the modifications needed for application to measurement data.

3.1 Time integration procedure

Starting from a measurement \({\varvec{u}}_m (\varvec{x}^{g}, {t_1})\) at time t 1 on a grid with N nodes at \({\varvec{x}}^g = \{{\varvec{x}}_1^g,\dots,{\varvec{x}}_N^g\}\), the time integration procedure consists of the following steps:

Step 1

The initial measured velocity vector field \({\varvec{u}}_m (\varvec{x}^{g},{t_1})\) must be free from large amplitude errors such as outliers. Therefore, the measured velocity field must first be subjected to outliers detection, removal and replacement (Westerweel 1994; Westerweel and Scarano 2005). The initial vorticity field \({\varvec{\omega}} (\varvec{x}^g, {t_1})\) is calculated from \({\varvec{u}}_m\) using a second-order central-difference scheme in the interior of the domain and first-order schemes on the measurement domain boundaries. The calculated vorticity field is the initial condition for the time integration procedure, and the computational grid is taken to be identical to the measurement grid with nodes at locations \({\varvec{x}}^g\).

Step 2

The divergence-free velocity field \({\varvec{u}} (\varvec{x}^g,{t_1})\) is calculated by solving Poisson Eq. (5) using the fast Fourier transform. This is a common approach, reported in the literature when dealing with the VIC method, to solve the Poisson equation on Cartesian grids (e.g. Cottet et al. 2002; Giovannini and Gagnon 2006). An efficient parallel implementation is detailed in Sbalzarini et al. (2006). At the initial time t 1 boundary conditions are taken from the measured velocity field at time t 1. For subsequent times, boundary conditions are approximated as explained in Sect. 3.2.

It should be remarked that the adoption of the divergence-free velocity field is intrinsic to the VIC time integration procedure. This is necessary to relate vorticity to velocity at each integration time step and is not meant as data preconditioning for noise reduction. Specific studies that impose a divergence-free condition to reduce measurement noise are due to Schiavazzi et al. (2013) and de Silva et al. (2013). The effect of obtaining a divergence-free reconstruction within the VIC procedure on the measurement noise is considered outside the scope of the present study and will not be further discussed here.

Step 3

The measurement domain is divided into N equal volumes V p i around each grid node (Fig. 3). In case of a uniform Cartesian 3D measurement domain V p i  = h 3, where h is the distance between grid nodes. A vortex particle is initialized in each volume V p i at the location of the grid node, \({\varvec{x}}_i^p(t_1)={\varvec{x}}_i^g\), with strength

$$\varvec{\alpha}{_i^p}(\varvec{x}{_i^p},{t_1}) = V_i^p \varvec{\omega}(\varvec{x}{_i^g},{t_1}).$$
(7)
Fig. 3
figure 3

Particle initialization at every grid point on a 2D Carthesian grid; the shaded area is the area V p i assigned to the black particle

Full size image

As mentioned by for example Kudela and Kosior (2011), clustering of particles tends to occur in regions with high velocity gradients. To prevent that particles gather together, particles are reinitialized on the grid nodes at each integration time step.

Step 4

Particle location at the next time step \({\varvec{x}}_i^p(t_1+\Updelta t)\) is calculated by solving Eq. (3) using first-order Euler integration,

$$\varvec{x}{^p_i}(t_1 + \Updelta t) = \varvec{x}{^p_i}(t_1) + \Updelta t \cdot \varvec{u}(\varvec{{x}}{^p_i},{t_1}),$$
(8)

where the integration time step \(\Updelta t\) is set as discussed in Sect. 3.3. After particle advection, the particles no longer coincide with the grid nodes, as illustrated in Fig. 2.

Step 5

Particle strength is updated to account for vortex stretching. The updated particle strength \({\varvec{\alpha}}(t_1+\Updelta t)\) is calculated by solving Eq. (4) using first-order Euler integration,

$$\varvec{\alpha}{_i^p}{(t_1} + \Updelta t) = \varvec{\alpha}{_i^p}{(t_1)} + \Updelta t \cdot \varvec{\alpha}{_i^p}{(t_1)} \cdot \varvec{\nabla} \varvec{u}(\varvec{x}{_i^p}{(t_1)},{t_1)},$$
(9)

where the spatial velocity derivatives are calculated using a second-order central-difference scheme.

Step 6

To calculate the velocity field \({\varvec{u}} (\varvec{x}{^g},{t_1}+{\Updelta t)}\) by solving Poisson Eq. (5), the vorticity field \({\varvec{\omega}}(\varvec{x}{^g},{t_1}+{\Updelta t)}\) is calculated on the grid nodes by

$$\varvec{\omega}(\varvec{x}{_i^g},{t}) = \frac{1}{h^3} \sum_{j=1}^N \varvec{\alpha}{_j^p} \varphi\left({\frac{\varvec{x}{_i^g} -\varvec{x}{_j^p}{(t)}}{{h}}}\right),$$
(10)

where \(\varphi({\varvec{x}})=\hat{\varphi}(x)\hat{\varphi} (y)\hat{\varphi}(z)\), with

$$\hat{\varphi}(x) = \left\{\begin{array}{ll} 0 & |x| \geq 2 \\ \frac{1}{2}\left({2-|x|}\right)^2\left({1-|x|}\right) & 1 < |x| < 2\\ 1-\frac{5}{2}x^2 + \frac{3}{2}|x|^3 & |x| \leq 1\\ \end{array}\right.$$
(11)

the third-order symmetric interpolation function, known as the M 4′ kernel introduced by Monaghan (1985) and given in Fig. 4 for completeness. The kernel conserves total circulation and linear and angular impulse and has been adopted in recent VIC simulations (see for example Ould-Salihi et al. 2000; Morgenthal and Walther 2007; Kosior and Kudela 2013).

Fig. 4
figure 4

Symmetric interpolation function M 4′ by Monaghan (1985)

Full size image

The interpolation kernel (11) is compact, chosen such that each particle influences 64 surrounding grid points (a 4 × 4 × 4 point kernel). Because one particle is initialized at each grid point, multiple particles will influence the vorticity at each grid point. Solving (10) directly by looping over all particles results in an inefficient loop. As suggested by Walther and Koumoutsakos (2001), the procedure can be vectorized when particles are ordered such that consecutive particles are at least 5 grid points apart in each spatial direction (Fig. 5). In this order, particles stored consecutively in memory assign their strength to different subsets of the mesh and the assignment procedure can be vectorized.

Fig. 5
figure 5

Particles are sorted such that consecutive particles influence different subsets of the mesh, as suggested by Walther and Koumoutsakos (2001); for example, the black particles assign their vorticity to different grid nodes

Full size image

To correct for the fact that vortex particles near the domain boundaries redistribute their vorticity to grid points outside of the computational domain, Cottet and Koumoutsakos (2000) suggest an iterative method. Also, for particles near a solid wall, a one-sided interpolation kernel is used by for example Chaniotis et al (2002) and Kudela and Kozowski (2009). To allow for a computationally efficient solution of the equations, in the present study, a vorticity boundary condition is overlayed over grid points on the domain boundary. The vorticity on the boundary is calculated from the velocity boundary conditions, which are approximated as explained in Sect. 3.2.

The velocity \({\varvec{u}}(\varvec{x}^g,{t_1}+\Updelta t)\) is subsequently calculated from \({\varvec{\omega}} (\varvec{x}{^g},{t_1}+\Updelta t)\) by solving Eq. (5) as in step 2 above. The integration procedure is repeated to calculate the velocity field at time \(t_1 + 2\Updelta t\) from the velocity field at \(t_1 + \Updelta t\) and onwards.

3.2 Boundary conditions

The value of velocity is known at the boundary of the domain only at the time instants corresponding to the measured samples. The latter correspond to the initial and final time of the calculation interval. Thus, the governing equations are ill-posed unless an estimate of the boundary conditions can be obtained from the available measurement data. Known boundary conditions, such as uniform flow (i.e. free-stream conditions), can be applied directly. On the other hand, unknown boundary conditions must be approximated. When the velocity is varying slowly along the boundary, a point-wise linear interpolation between consecutive measurements can be considered an acceptable approximation. If unsteady conditions involve the boundaries of the domain a possibly better approximation can be made using the advection model by Scarano and Moore (2011). This technique was used previously by Sciacchitano et al (2012) to estimate boundary conditions required when solving the Navier–Stokes equations to fill spatial gaps in PIV measurements.

The advection model estimates the velocity at time t in between two measurements at time T 1 and T 2 by solving

$$\varvec{u}(\varvec{x}{^g_i},{t}) = \frac{T_2-t}{\Updelta T}\varvec{u}(\varvec{x}{_1},{T_1}) + \frac{t-T_1}{\Updelta T}\varvec{u}(\varvec{x}{_2},{T_2}),$$
(12)

where the locations \({\varvec{x}}_1\) and \({\varvec{x}}_2\) are found by solving

$$\varvec{x}{_1} = \varvec{x}{^g_i} - \varvec{u}_{{\rm c}} \cdot (t - T_1),$$
(13)
$$\varvec{x}{_2} = \varvec{x}{^g_i} + \varvec{u}_{{\rm c}} \cdot (T_2 - t).$$
(14)

The convective velocity \({\varvec{u}}_c\) is estimated following an iterative procedure, with an initial estimate based on the local velocity, as explained by Scarano and Moore (2011).

3.3 Integration time step \(\Updelta t\)

Inviscid vortex methods are not limited by classical CFL-type stability conditions. As noted by for example Cottet and Poncet (2003) and Chatelain et al. (2008), Lagrangian particle advection is linearly unconditionally stable, and for nonlinear stability, it is sufficient that particles do not collide. This imposes a limit on the time step related to the rate of strain of the flow,

$$\Updelta t_1 \leq \left|\left| \nabla \boldsymbol{u}\right| \right|_\infty^{-1}.$$
(15)

This condition does not involve the mesh size and is often less restrictive than a classical CFL condition.

To allow for vectorization and simplify implementation of the assignment procedure where the vorticity field is calculated on the grid from advected vortex particles, it is assumed that each particle does not move more than the mesh cell size h in each spatial direction over the integration time \(\Updelta t\). This leads to a restriction on the maximum time step, which is identical to the standard CFL condition,

$$\Updelta t_2 \leq \left|\left|\frac{\boldsymbol{u}}{h}\right| \right|_\infty^{-1}.$$
(16)

A third pragmatic constraint on the maximum time step follows simply from the desired sampling frequency:

$$\Updelta t_3 \leq f_{{\rm super\_sampled}}^{-1}.$$
(17)

In view of the stability conditions discussed in this section, it should be remarked that reducing the mesh spacing h does not result in the growth of instabilities when the conditions above are satisfied. However, a challenging requirement is posed in terms of spatial resolution for evaluation of vorticity in the first step of the VIC time integration procedure (Sect. 3.1). Tomographic PIV measurements do not typically resolve the wide range of scales in the turbulent flow regime at high Reynolds numbers (Westerweel et al. 2013). As a result, the limited spatial resolution generally leads to underestimation of the initial vorticity and consequently amplitude of the reconstructed velocity fluctuations.

4 Reconstruction accuracy error estimate

The proposed vortex method for time-supersampling is regarded as a physics-based interpolation technique. The accuracy of the reconstructed velocity field is dependent upon a number of factors: the measurement accuracy of the initial conditions and that of the estimated boundary conditions; the quality of the flow model (e.g. the validity of neglecting viscosity); and the numerical error in the model discretization. However, firstly there are hard information-theoretical limits on the maximum length of the reconstructed time segment.

4.1 Maximum integration time

A theoretical maximum integration time can be derived from the simplified case of scalar convection, as the time it takes for the information contained in the measured flow field to be convected out of the measurement domain,

$$T < \frac{L_{{\rm d}}}{V_{{\rm c}}},$$
(18)

where L d is the length of the measurement domain in direction of the dominant convective velocity V c . The inverse directly yields the relevant requirement on the minimum acquisition frequency for a given measurement,

$$f_{{\rm acq}} > \frac{V_{{\rm c}}}{L_{{\rm d}}}.$$
(19)

This frequency most often lies far below the frequency dictated by the Nyquist criterion for reconstruction of a signal from its discrete samples. The ratio between the Nyquist frequency criterion and V c /L d gives an indication of the sub-sampling margin potentially usable within an experiment.

4.2 A posteriori estimate of the reconstruction accuracy

The accuracy of the reconstruction is estimated using the Euclidean norm of the difference between the solutions produced by forward and backward time marching. This approach has already been proposed in a previous work (Scarano and Moore 2011); however, an improved estimate is obtained by averaging differences at all reconstructed time steps within one measurement interval, weighted according to proximity to a measurement plane:

$$\varepsilon_{{\rm est.}} = \frac{100}{V_{{\rm ref}}} \left[{\frac{1}{\sum_{n=1}^N w_n} \sum\limits_{n=1}^N \frac{w_n}{4} \left|\left|{\user2{u}_{f,n} - \user2{u}_{b,n}}\right|\right|^2} \right]^{1/2}.$$
(20)

The weights w n are calculated from the tent function,

$$w_n = \left\{\begin{array}{ll} t_n-T_{1} & t_n-T_{1} \leq \frac{1}{2}\Updelta {\rm T} \\ T_2-t_n & t_n-T_{1} > \frac{1}{2}\Updelta {\rm T}\\ \end{array}\right.,$$
(21)

where t n is a time between two subsequent measurements at T 1 and T 2 and \(\Updelta T = T_2-T_1\). In the present work, this error estimate will be evaluated and compared to the actual reconstruction error calculated using reference measurements.

5 Experimental assessment

Supersampling of 3D PIV time-resolved sequences is considered for two experimental datasets that are detailed in literature and available to the authors. The assessment of the method is made by comparing reconstructions made using the VIC method to reference measurements in order to determine the direct reconstruction error. Additionally, the method is compared with two other reconstruction techniques: the first is point-wise linear interpolation; the second makes use of the advection equation (Scarano and Moore 2011).

The assessment method considers the measurements as ‘ground truth’. The PIV measurement rate f m is decreased artificially to f s by sub-sampling the original data set (Fig. 6) according to a sub-sampling factor (SSF),

$$\hbox{SSF} = \frac{f_{m}}{f_{s}}.$$
(22)
Fig. 6
figure 6

Illustration of reference measurements sub-sampled with SSF = 6; the dashed line represents a linear interpolation through the sub-sampled measurements

Full size image

Subsequently, time-supersampling is applied to the sub-sampled velocity fields and the resulting velocity fields are compared to the original time series. This is first done qualitatively by visual comparison with the measured velocity fields in the spatial and time domains. For a quantitative comparison, the metric used for the reconstruction uncertainty in the reconstructed velocity \({\varvec{u}}_{{\rm TSS}}\) is the Euclidean norm for all velocity components normalized by a reference velocity,

$$\varepsilon = \frac{100}{V_{{\rm ref}}} \left[{\frac{1}{N} \sum_{n=1}^N \left|\left|{\user2{u}_{{\rm TSS}}(\user2{x},t_n) - \user2{u}_{{\rm m}}(\user2{x},t_n)} \right|\right|^2}\right]^{1/2}.$$
(23)

5.1 NACA airfoil trailing edge flow

In this first case, a fully developed turbulent boundary layer leaves the trailing edge of a NACA 0012 airfoil. The set-up of the tomographic PIV experiment is illustrated in Fig. 7. Measurements are performed on a 40-cm chord airfoil at a free-stream velocity of 14 m/s. The resulting Reynolds number based on chord length is Re C  = 386,000, and based on the boundary layer, momentum thickness is Re θ = 1,300. The full description of the experiment is given in Ghaemi and Scarano (2011) and salient features of the dataset are given in Table 1.

Fig. 7
figure 7

The arc-like arrangement of the cameras, airfoil and the multi-pass illumination system in the tomographic PIV experiment (figure reproduced from Ghaemi and Scarano 2011)

Full size image
Table 1 Turbulent wake flow measurement conditions
Full size table

To fulfil the light demand of the tomographic PIV experiment, the laser beam is introduced in a multi-pass light amplification system to increase illumination intensity in the measurement domain (Ghaemi and Scarano 2011). The measurement volume extends for approximately 5 times the boundary layer thickness along the streamwise and spanwise directions. The volume thickness of 8 mm is slightly less than that of the boundary layer (δ 99 = 10 mm) before the trailing edge. The recording system is composed of four Photron Fastcam CMOS imagers. Even with such an arrangement, the tomographic system could not be used at a rate beyond 2,700 image pairs/second, which was at the limit of temporal resolution for the sub-structures detected in the boundary layer. As a result, a fluid parcel at the outer edge of the boundary layer travels approximately 5 mm (0.5δ) between subsequent measurements and will appear approximately 10 times in the measurement domain before exiting it downstream. Accordingly, the maximum SSF calculated by Eq. (18) from the minimum frequency of the sub-sampled dataset equals approximately SSFmax = 10.

The flow in the near wake of the airfoil features the typical pattern of fully developed turbulent boundary layers with elongated low- and high-speed streaks (Fig. 8). Most vortical structures, cane vortices and hairpin packets, concentrate across the low-speed regions, where ejections are more pronounced (Tomkins and Adrian 2003). In the near wake region behind the airfoil, Taylor’s hypothesis of ‘frozen turbulence’ holds reasonably well and supersampling by advection has been demonstrated to be an accurate approach for increasing temporal resolution (Scarano and Moore 2011). Therefore, this case has been chosen to verify whether the VIC method is able to reconstruct the time-resolved velocity fields in conditions where the advection-based model can be considered as a reference technique.

Fig. 8
figure 8

Organization of low-speed (blue/dark grey) and high-speed (green/light grey) streaks (\(u'/U_{\infty} = \pm0.08\)) within the wake region behind a NACA-0012 airfoil

Full size image

The time history of the velocity at a point in the centre of the measurement domain is shown in Fig. 9 for the case of SSF = 4 and SSF = 8. As explained before, the reference measurements are sub-sampled, resulting in a coarser dataset (circled labels in Fig. 9). Subsequently, the data are supersampled using different techniques. The temporal fluctuations of the streamwise velocity component have a typical time scale slightly less than 1 ms (Ghaemi and Scarano 2011). In this respect, the current measurement rate of 2.7 kHz is just sufficient to describe these fluctuations and it is expected that even at low SSF the reconstruction by linear interpolation would fail to reconstruct temporal fluctuations.

Fig. 9
figure 9

Time history of the streamwise velocity component in the centre of the measurement domain, reconstructed by point-wise linear interpolation, advection model and VIC. SSF = 4 (top) and SSF  = 8 (bottom)

Full size image

This is readily verified by inspection of the time series in Fig. 9, where it is shown that when sub-sampling from 2.7 kHz to 675 Hz (SSF = 4), the linear interpolation fails to reconstruct the temporal velocity fluctuations, with most fluctuations of time scales smaller than 2 ms being clipped. In contrast, both the advection and VIC method appear to be adequate as they return a velocity field temporal evolution with a good qualitative agreement with the measured reference data series. It should be noted that the reconstruction by advection passes exactly through the sub-sampled data. In contrast, the reconstruction obtained with the VIC method does not, since a divergence-free velocity field is produced from the actual datasets. For illustration, the divergence-free VIC reconstruction at each measurement time instant (essentially SSF = 1) is also plotted in the velocity time series (blue crosses). The difference between the reconstruction at SSF = 1 and the measurements is approximately 1.4 % of the free-stream velocity, calculated by Eq. (23), posing a minimum to the attainable reconstruction error. It should be noted that a component of such difference is also due to the measurement errors present in the original measurements.

When the sampling frequency is reduced further to 337.5 Hz (SSF = 8), the reconstruction accuracy of both the advection and VIC models degrades, which is confirmed by the summary of reconstruction errors given in Table 2. In calculating these relative errors, the free-stream velocity is used as reference velocity and a dataset of 100 snapshots is considered. The last column shows the a posteriori error estimate \(\varepsilon_{{\rm VIC,a-post}}\) based on the backward and forward integration only and calculated using Eq. (20), for comparison with the direct error \(\varepsilon_{{\rm VIC}}\) calculated from comparison with the reference measurements.

Table 2 Reconstruction errors for the turbulent wake case, calculated in the centre of the measurement domain as a percentage of the free-stream velocity
Full size table

Even for a potentially exact reconstruction by supersampling, the measurement noise and quality of the reconstruction at SSF = 1 give a lower bound on the error. In the present experiment, the measurement uncertainty has been estimated to be approximately 1.5 % of the free-stream velocity based on the analysis of the velocity divergence, which is only slightly in excess of the measurement uncertainty of 1.3 % estimated in Scarano and Moore (2011) for a planar PIV measurements conducted on the same experiment. It is therefore expected that the reconstruction error is overestimated by a similar amount.

Comparing the reconstruction errors in Table 2 to the estimated measurement error shows that the additional error introduced by supersampling using a linear interpolation is significantly larger than the measurement error. The situation is improved substantially by using both the advection and vortex models. For supersampling using the linear advection model, it remains in the same order up to approximately SSF = 4 and the additional error from supersampling using the vortex model remains smaller than the measurement error for SSF < 6.

Comparison of the a posteriori error estimate \(\varepsilon_{{\rm VIC,a-post.}}\) calculated using Eq. (20) to the direct error shows the values are in good agreement, which indicates that the a posteriori error estimate from Eq. (20) may be taken as an estimator for the reconstruction quality. For low SSF, the error estimate is smaller than that of the direct error, which is explained by the presence of measurement noise.

As expected from the previous discussion, the spatial distribution of the reconstruction error (Fig. 10) of VIC and linear advection are comparable for SSF = 4. With a coarser time resolution (SSF = 8), the direct error estimate calculated for the VIC technique is slightly lower than that observed for the advection model. The situation near the inflow and outflow boundaries shows an increase in the error and a more equivalent result between the two methods, as the boundary conditions used for the VIC reconstruction are equal to the solution of the advection equation on the boundaries. Inside of the measurement domain the vortex method improves upon the advection model. In particular, closer to the airfoil trailing edge, the VIC model improves upon the advection model, which is explained by the stronger velocity deficit (30 %) at the inflow region of the measurement domain. This makes the flow regime at the left boundary not well approximated by pure advection and explains the larger reconstruction errors for the advection model.

Fig. 10
figure 10

Relative reconstruction error due to reconstruction from the advection and vortex models in the plane y = 0 with SSF = 4 and SSF = 8

Full size image

5.2 Transitional circular jet

The second case is that of a transitional circular jet (Fig. 11). A contoured nozzle with exit diameter D = 10 mm is installed at the bottom wall of a water tank. The tomographic PIV measurements are performed with a jet exit velocity of 0.5 m/s yielding a Reynolds number Re D  = 5,000 based on the jet diameter D. The relevant experimental parameters are listed in Table 3 and a full discussion of the experimental parameter set-up is available in Violato and Scarano (2011).

Fig. 11
figure 11

Reference measurements (top) compared to reconstructed velocity fields at SSF = 30 using a linear interpolation, the advection model and the vortex method; the isosurfaces show vortices identified by the Q-criterion (green) and the axial velocity component v = 8 vox/ms (yellow)

Full size image
Table 3 Experimental parameters for the transitional jet following Violato and Scarano (2011)
Full size table

For the jet flow, less accurate results were obtained using the advection model, and therefore, it is chosen as a second test case for the VIC method. The free shear layer is dominated by the Kelvin-Helmholtz instability, and strong vortices are shed at approximately 30 Hz (Strouhal number of 0.67). The hypothesis of frozen turbulence is not valid in this region, which as discussed in Scarano and Moore (2011) invalidates the assumptions made by the advection model.

The flow field is visualized in Fig. 11, which shows isosurfaces for the axial velocity component and the Q-criterion that identifies vortical structures (Hunt et al. 1988). The tomographic measurements are done with a repetition rate of 1,000 Hz, whereby the vortex shedding (at 30 Hz) is captured with very high temporal resolution. Based on the jet exit velocity, the theoretical maximum SSF is estimated by Eq. (18) to be approximately SSFmax = 90. However, as will be shown, the practical maximum SSF equals 60. This value still represents quite an extreme as it corresponds to a sampling frequency of only 16.7 Hz, which is about one quarter of the frequency required by the Nyquist criterion.

The three-dimensional velocity field is calculated using the fluid trajectory correlation (FTC) algorithm as introduced by Lynch and Scarano (2013) as the technique yields time accurate measurements with significant error reduction. Consequently, both reconstruction quality and a posteriori reconstruction error estimate will be shown to benefit greatly from reduced measurement noise. Based on results for low SSF of 5 for both advection and VIC, where the sub-sampled and reference time series are both sampled significantly above Nyquist and the reconstruction errors can be ascribed mostly to measurement uncertainties, the estimated measurement error is approximately 0.8 % of the jet exit velocity.

Figure 12 shows the time history of the radial and axial velocity components at a point within the shear layer (x/D = −0.33, y/D = 2.5, z/D = 0). The VIC divergence-free reconstruction plotted in this figure (blue crosses) at SSF = 1 shows, with a difference of approximately 0.4 % of the jet exit velocity, good correspondence with the reference measurements. Considering that the period of the temporal fluctuations equals approximately 30 ms (vortex shedding), when the data are sub-sampled with SSF = 30, the resulting frequency becomes half of that dictated by the Nyquist criterion. Not surprisingly, the linear interpolation is unable to reconstruct the velocity fluctuations as illustrated in Fig. 12. Furthermore, the advection model completely fails to reconstruct the fluctuations at this low sampling frequency, as the assumption of linearized trajectories does not hold. In contrast, the VIC method is able to accurately reconstruct the velocity fluctuations, even though the sampling frequency is reduced to the vortex shedding frequency. Some numerical dissipation effects are noticeable, with a reduction in amplitude of the axial velocity fluctuations of approximately 4 %. This is still considered small in comparison to damping effects of up to 40 % reported in Sciacchitano et al. (2012) in a study regarding simulation of the Navier–Stokes equations to fill data gaps in PIV measurements. A further reduction in sampling frequency to 22 Hz (SSF = 45) shows further reduction in amplitude of the temporal velocity fluctuations for the VIC method and a more pronounced damping effect. No phase distortion could be noticed.

Fig. 12
figure 12

Reconstructed time histories of the streamwise and axial velocity components in a point in the shear layer at (x/D, y/D, z/D)  = (−1/3, 5/2, 0), using point-wise linear interpolation, the advection model and the proposed vortex method for SSF = 30 (top) and SSF = 45 (bottom)

Full size image

To analyse the spatial patterns produced by the different reconstructions, the case of SSF = 30 is taken and the temporal evolution of the jet is depicted at three time instants (Fig. 11). The animation of the full temporal evolution is provided with supplementary files. The top plots show the reference measurements. The bottom three, respectively, show reconstruction by linear interpolation, the advection model and the VIC method. At t = 0 ms, the linear interpolation and advection model are equal to the reference measurements, whereas the VIC reconstruction shows some minor difference, due to the divergence-free condition. Already 5 ms later, both the linear interpolation and advection model cannot reconstruct the fluctuations as expected from the previous discussions. The VIC method however captures the correct phase and location of the vortex rings. Further at t = 15 ms, the reconstruction is at the middle time between two sub-sampled measurements. At this time instant, the error is expected to be largest, given the weighted scheme used to combine forward and backward integration. The advection model reconstruction essentially breaks apart the coherent vortices and is clearly inadequate to reconstruct this velocity field with strong flow shear and rotation. In contrast, the VIC method appears to reconstruct the velocity field rather accurately without any visible distortion.

The reconstruction error, normalized using the jet exit velocity, is given in Table 4 at a position in the free shear layer. As shown in Fig. 13, which gives the spatial distribution of the reconstruction error for SSF = 30, the largest errors are occurring in the shear layer. From both the table and figure, one can see the rapid increase in the reconstruction error of the advection model when increasing SSF. The error reaches a maximum of approximately 10 % for SSF >30 and remains constant after that. This indicates that the discrepancy between the reconstructed value, and the actual value has reached the same order as that of the physical velocity fluctuations. The vortex method maintains reconstruction errors within 2 % up to SSF = 50 (f s  = 20 Hz) confirming its suitability for these type of flows.

Table 4 Reconstruction errors for the transitional jet case in the shear layer at x/D =  − 1/3, y/D = 5/2 and z = 0 as a percentage of the jet exit velocity
Full size table
Fig. 13
figure 13

Relative reconstruction errors in the plane Z/D = 0 with SSF = 30. Linear interpolation (left), advection model (middle) and the proposed vortex model (right)

Full size image

It should be remarked that for this case, the measurement noise is significantly lower than in the case of the turbulent wake. The higher precision of the measurements increases in turn the reconstruction quality and decreases the value of the estimated error. As can be shown in Table 4, the a posteriori error estimate calculated using (20) becomes a rather accurate estimator for the reconstruction error in this case.

As discussed earlier, the maximum value of SSF that can be theoretically applied to this experiment is approximately 90. The practical maximum value of SSF however cannot be increased beyond 60 due to the uncertainty in the boundary conditions, which in this case cannot be estimated accurately by the advection model. Increasing SSF from 50 to 60 already increases the reconstruction error substantially (Table 4). However, the latter case is already rather extreme (SSF = 60), as it corresponds to a measurement rate reduced from 1,000 Hz to only 16.7 Hz, or half the shedding frequency and one quarter of the required sampling frequency according to the Nyquist criterion. Furthermore, it has been shown that a stable reconstruction is possible when reducing the sampling frequency to the vortex shedding frequency (SSF = 30). The numerical dissipation is shown to increase when further reducing the measurement rate. At SSF = 45 (f s  = 22 Hz), these effects account for a reduction in amplitude of the axial velocity fluctuations of approximately 9 %. On the other side, it should be remarked that these results were obtained by time-supersampling tomographic PIV measurements with sufficient spatial resolution for evaluation of vorticity from spatial velocity derivatives. Decreasing the spatial resolution is also expected to play a role on the expected numerical dissipation (see for instance Tokgoz et al. 2012).

6 Conclusions

The VIC technique based on numerical solution of Navier–Stokes equations is proposed to increase the temporal resolution of time-resolved tomographic PIV experiments. The numerical solution is evaluated on a domain that corresponds to the 3D measurement volume, and time integration is performed between each pair of consecutive measurements to achieve a temporal resolution not available from the original measurements. The measured data serves as initial conditions for the VIC method simulating the fluid flow dynamical evolution, and in this way, the spatial resolution available by the measurements is projected into time.

The VIC method is compared to linear interpolation and an advection-based approach. Two experimental test cases are selected to evaluate the applicability of the method to real measurement conditions. In the case of the turbulent wake, where Taylor’s hypothesis of frozen turbulence holds to a good extent, both the advection model and VIC method are able to accurately reconstruct temporal velocity fluctuations. Secondly, in the case of a transitional jet, where the free shear layer is dominated by strong vortices that roll-up under the effect of the Kelvin-Helmholtz instability, the advection model essentially fails to represent the strongly nonlinear physics caused by the vortices in the shear layer. In contrast, the VIC method accurately reconstructs the velocity time series, even when the sampling rate is reduced to a fraction of the Nyquist frequency.

The study demonstrates that the sampling rate requirements for tomographic PIV can be strongly reduced when the data are time-supersampled using the VIC method. The main advantage can be seen as twofold: on the one side, the reduced measurement rate requirements allow higher laser pulse energy for larger measurement domains; at the other end, we anticipate that in high-speed flows (e.g. V∼100 m/s), time-resolved information can still be obtained with the combination of tomographic PIV and VIC, thereby extending the range of applicability of 4D-PIV by tomographic PIV or similar techniques. The discussion also illustrates the potential for a wider application of the VIC method to 3D PIV measurements, including pressure from PIV and spectral estimation, which is a subject for further work.