Stochastic nonlinear model for somatic cell population dynamics during ovarian follicle activation

Abstract

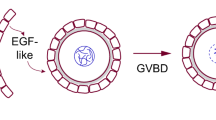
In mammals, female germ cells are sheltered within somatic structures called ovarian follicles, which remain in a quiescent state until they get activated, all along reproductive life. We investigate the sequence of somatic cell events occurring just after follicle activation, starting by the awakening of precursor somatic cells, and their transformation into proliferative cells. We introduce a nonlinear stochastic model accounting for the joint dynamics of the two cell types, and allowing us to investigate the potential impact of a feedback from proliferative cells onto precursor cells. To tackle the key issue of whether cell proliferation is concomitant or posterior to cell awakening, we assess both the time needed for all precursor cells to awake, and the corresponding increase in the total cell number with respect to the initial cell number. Using the probabilistic theory of first passage times, we design a numerical scheme based on a rigorous finite state projection and coupling techniques to compute the mean extinction time and the cell number at extinction time. We find that the feedback term clearly lowers the number of proliferative cells at the extinction time. We calibrate the model parameters using an exact likelihood approach. We carry out a comprehensive comparison between the initial model and a series of submodels, which helps to select the critical cell events taking place during activation, and suggests that awakening is prominent over proliferation.

Appendix

1.1 Justification of the choice of the rate of $\mathcal {R}_2$

As detailed in Sect. 4.5 the auto-amplification can result from two non-exclusive mechanisms, a nonlocal (global) one and a local one.

Global amplification considers that each proliferative cell sends a fixed amount of growth signals to the oocyte. The oocyte thus receives a signal proportional to the number of proliferative cells C. We consider that the oocyte secrete in turn (instantaneously) a stimulatory signal, at a level proportional to the amount of growth signals received from somatic cells. By homogeneous diffusion, the oocyte signal is shared equally to all somatics cells, so that each precursor cell receives a signal proportional to $C/(F+C)$.

Local amplification for a given precursor cell, assuming a random repartition of the cell types around the oocyte (hence neglecting local cell-to-cell effects), the probability that a neighbor cell is a proliferative cell is $C/(F+C-1)$, which is also consistent with our choice.

1.2 Mean-field formulation

To get some insight into the model behavior, we describe the mean-field version of model $\mathcal {M}_{FC}$, given by the following set of ODE:

$$\begin{aligned} \left\{ \begin{array}{c} \frac{d}{dt}f(t) = - \alpha _1 f(t) - \beta f(t) \frac{c(t)}{f(t) + c(t)}, \\ \frac{d}{dt}c(t) = (\alpha _1 + \alpha _2)f(t) + \beta f(t) \frac{c(t)}{f(t) + c(t)} +\gamma c(t), \end{array} \right. \end{aligned}$$

(20)

with the initial condition $(f(0), c(0)) = (f_0, 0)$, with $f_0 \in \mathbb {R}_+$. We start by solving analytically the deterministic formulation, and then investigate the effect of each parameter on the model outputs.

From the ODE system (20), we deduce the change in the proliferative cell proportion $p_C(t) := \frac{c(t)}{f(t) + c(t)}$:

$$\begin{aligned} \frac{d}{dt}p_C(t)= & {} \alpha _1 + \alpha _2 - (\alpha _1 + 2 \alpha _2 - \beta - \gamma )p_C(t) + (\alpha _2 - \beta - \gamma )p_C(t)^2 \nonumber \\= & {} (\alpha _2 - \beta - \gamma ) (p_C(t) - 1) (p_C(t) - \frac{ \alpha _1 + \alpha _2}{\alpha _2 - \beta - \gamma }). \end{aligned}$$

(21)

From ODEs (20) and (21), using the classical method of separation of variables, we can compute the analytical expressions for the proliferative cell proportion $p_C(t)$, proliferative cell number c(t) and precursor cell number f(t):

Proposition 5

The solution of the ODE system (20) is, for all $t\ge 0$,

$$\begin{aligned} f(t)= & {} f_0\exp \left( - \alpha _1 t - \beta \int _{0}^{t}p_C(s)ds \right) , \\ c(t)= & {} f_0 \left( \exp \left( \alpha _2 t + (\gamma - \alpha _2) \int _{0}^{t} p_C(s)ds\right) - \exp \left( - \alpha _1 t - \beta \int _{0}^{t}p_C(s)ds \right) \right) . \end{aligned}$$

In addition, the solution of ODE (21) is

$$\begin{aligned} p_C(t) = \frac{1 - \exp \left( -(\alpha _1 + \beta + \gamma )t\right) }{1 - \frac{\alpha _2 - \beta - \gamma }{\alpha _1 + \alpha _2}\exp \left( -(\alpha _1 + \beta + \gamma )t\right) } . \end{aligned}$$

(22)

and the total cell number verifies

$$\begin{aligned} n(t) := f(t) + c(t)= f_0 \exp \left( \alpha _2 t + (\gamma - \alpha _2) \int _{0}^{t} p_C(s)ds\right) . \end{aligned}$$

From Proposition 5, it is clear that the proliferative cell proportion $p_C$ converges to 1. If $\gamma >0$, the proliferative cell number c grows asymptotically exponentially at a rate $\gamma$ when $t\rightarrow \infty$. If $\gamma =0$, c(t) is bounded because $t\mapsto 1-p_C(t)$ is converging exponentially fast to 0, hence is integrable on $(0,\infty )$. Moreover, the proliferative cell proportion $p_C$ has an inflexion point if and only if

$$\begin{aligned} \beta +\gamma >\alpha _1+2\alpha _2. \end{aligned}$$

An inflexion point denotes the presence of at least two distinct phases, with a first progressive acceleration phase followed by a saturating phase.

Finally, note that according to the observed variables, the submodels cannot be distinguished from one another, or, alternatively, different parameter values (within a same submodel) may lead to identical outputs. Indeed, the changes in the precursor cell population are independent of parameters $\alpha _2,\gamma$, and, more strikingly, parameters $\beta$ and $\gamma$ cannot be separated in the analytical solution (22), leading to the same kinetic patterns for $p_C$ as long as the combination $\gamma + \beta$ remains unchanged.

1.3 Analytical expressions in the linear case

Proof of Proposition 1

Let $t \ge 0$ and $f \in \llbracket 0, f_0 \rrbracket$. Since $F_t$ is autonomous and is a pure death process, we can directly write the following forward Kolmogorov equation: for all $f \in \llbracket 0, f_0 \rrbracket$,

$$\begin{aligned}&\frac{d}{dt}\mathbb {P}\left[ F^L_t = f |F_0 = f_0\right] \nonumber \\&\quad \alpha _1(f + 1) \mathbb {P}\left[ F^L_t = f+1 |F_0 = f_0\right] - \alpha _1 f \mathbb {P}\left[ F^L_t = f |F_0 = f_0\right] . \end{aligned}$$

(23)

Solving by recurrence (23), we deduce that, for all $f \in \llbracket 0, f_0 \rrbracket$,

$$\begin{aligned} \mathbb {P}\left[ F^L_t = f | F_0 = f_0\right] = \genfrac(){0.0pt}0{f_0}{f} (e^{ - \alpha _1 t})^f(1 - e^{ - \alpha _1 t})^{f_0 -f}. \end{aligned}$$

Note that $\mathbb {P}\left[ F_t^L = 0 | F_0 = f_0 \right] = (1 - e^{-\alpha _1 t})^{f_0}$ which converges to 1 when $t\mapsto 1-p_C(t)$. Hence, process $F^L$ extincts almost surely (a.s.) when t goes to infinity, hence $\tau _L< \infty$. Before computing the law of $\tau _L$, we can directly obtain its mean using the recursive expression (4):

$$\begin{aligned} \mathbb {E}\left[ \tau _L\right] = \sum _{k = 0}^{f_0 - 1} \mathbb {E}\left[ T_{k + 1} - T_k \right] = \sum _{k = 0}^{f_0 - 1} \mathbb {E}\left[ \mathcal {E}\left( \alpha _1 (f_0 - k)\right) \right] = \frac{1}{\alpha _1}\sum _{k = 1}^{f_0}\frac{1}{k}. \end{aligned}$$

Using again Eq. (4), we deduce that $\tau _L(= T_{f_0})$ follows a generalized Erlang law whose density function is:

$$\begin{aligned} f_{\tau _L}(t) = \mathbb {1}_{t \ge 0} \sum _{i = 0}^{f_0 - 1} \prod _{j \ne i, j = 0}^{f_0 - 1}\frac{f_0 -j}{i - j} \alpha _1 (f_0 - i)e^{-\alpha _1(f_0 - i)t}. \end{aligned}$$

(24)

Due to the specific form of the exponential rate, we can simplify Eq. (24) further. As $\displaystyle \prod _{j \ne i, j = 0}^{f_0 - 1}(f_0 -j) = \frac{f_0 !}{f_0 - i}$ and

$$\begin{aligned} \displaystyle \prod _{j \ne i, j = 0}^{f_0 - 1} (i - j) =&\displaystyle \prod _{j= 0}^{i-1} (i-j) \times \prod _{j= i+1}^{f_0 - 1} (i - j) \\&= i! (-1)^{f_0 - 1 - i} \prod _{j= 1}^{f_0 - 1 - i} j = (-1)^{f_0 -1 - i}i !(f_0 - 1 - i) !, \end{aligned}$$

we deduce

$$\begin{aligned} f_{\tau _L}(t)&= \alpha _1 \mathbb {1}_{t \ge 0} \sum _{i = 0}^{f_0 - 1} \frac{f_0 !}{i !(f_0 - 1 - i) !} (-1)^{f_0 - 1 - i} e^{-\alpha _1(f_0 - i)t} \\&=\alpha _1 f_0 e^{-\alpha _1t}\mathbb {1}_{t \ge 0} \sum _{i = 0}^{f_0 - 1} \genfrac(){0.0pt}0{f_0 - 1}{i} (-e^{-\alpha _1t})^{f_0 - i - 1}\\&= \alpha _1 f_0 e^{-\alpha _1t} (1 - e^{-\alpha _1t})^{f_0 - 1}\mathbb {1}_{t \ge 0}. \end{aligned}$$

$\square$

Proof of Proposition 2

According to Proposition 1, $\tau _L$ is a.s. finite. To take the expectation of $C^L_t$ at time $t = \tau _L$, we check that $\mathbb {E}\left[ C^{k,j}_{\tau _L- T_k^j} \right] < \infty$, for all k and j. For all $t \ge 0$, $C_t^{k,j}$ is $L_1-$integrable (as a Yule process) with $\mathbb {E}\left[ C^{k,j}_{t} \right] = e^{\gamma t}$. Conditionning on the law of $\tau _L$, we get (with the change of variables $x=1-e^{-\alpha _1 t}$)

$$\begin{aligned} I&:=\mathbb {E}\left[ C^{k,j}_{\tau _L} \right] = \int _{0}^{+ \infty } e^{\gamma t} f_{\tau _L}(t)dt = f_0 \int _{0}^{+ \infty }e^{\gamma t}(1 - e^{-\alpha _1 t})^{f_0 - 1}\alpha _1e^{- \alpha _1t} dt \\&= f_0 \int _0^1 (1-x)^{-\frac{\gamma }{\alpha _1}}x^{f_0-1}dx=f_0B\left( f_0,1-\frac{\gamma }{\alpha _1}\right) \end{aligned}$$

where B is the standard Beta function. Hence $I < \infty$ if and only if Hypothesis 3 holds. Note that using the properties of the Beta function, we have

$$\begin{aligned} I=\frac{f_0!}{\left( f_0-\frac{\gamma }{\alpha _1}\right) !}, \end{aligned}$$

(25)

where we use the notation $\left( m-x\right) !=\prod _{k=1}^m (k-x)$. Thus, if Hypothesis 3 holds true, and given that $C^{k,j}$ is a positive increasing process, we deduce:

$$\begin{aligned} \mathbb {E}\left[ C^{k,j}_{\tau _L- T_k^j} \right] \le \mathbb {E}\left[ C^{k,j}_{\tau _L} \right] < \infty . \end{aligned}$$

Then, taking the expectation of (6) at time $t = \tau _L$, we obtain:

$$\begin{aligned} \mathbb {E}\left[ C^{L}_{\tau _L} \right] = \sum _{k = 1}^{f_0} \mathbb {E} \left[ C^{k,0}_{\tau _L- T_k^0} \right] + \sum _{k = 0}^{f_0 - 1} \mathbb {E} \left[ \sum _{j = 1}^{N_k(\tau _L)} C^{k,j}_{\tau _L- T_k^j} \right] . \end{aligned}$$

(26)

Moreover, we have that each counting process $N_k(t)$ can be dominated by

$$\begin{aligned} N_k(t) \le \mathcal {Y}_3 \left( \alpha _2 f_0 t\right) , \end{aligned}$$

so that

$$\begin{aligned} \sum _{j = 1}^{N_k(\tau _L)} C^{k,j}_{\tau _L- T_k^j} \le \sum _{j = 1}^{\mathcal {Y}_3(\tau _L)} C^{k,j}_{\tau _L}. \end{aligned}$$

Finally, conditionally on $\tau _L$, $\mathcal {Y}_3(\tau _L)$ is independent of each $C^{k,j}_{\tau _L}$, and the latter are independent and identically distributed random variables. Using that

$$\begin{aligned} \mathbb {E}\left[ \sum _{j = 1}^{\mathcal {Y}_3(\tau _L)} C^{k,j}_{\tau _L} \right] = \mathbb {E}\left[ \mathbb {E}\left[ \sum _{j = 1}^{\mathcal {Y}_3(\tau _L)} C^{k,j}_{\tau _L} \mid \tau _L\right] \right] , \end{aligned}$$

and the Wald equation (Feller 1967, Chap. XII), we obtain

$$\begin{aligned} \mathbb {E} \left[ \sum _{j = 1}^{N_k(\tau _L)} C^{k,j}_{\tau _L- T_k^j} \right] \le \alpha _2 f_0 \int _{0}^{+ \infty } t e^{\gamma t} f_{\tau _L}(t)dt, \end{aligned}$$

which is finite under Hypothesis 3. Finally, if Hypothesis 3 does not hold, we have, as long as $f_0\ge 2$:

$$\begin{aligned} \mathbb {E} \left[ C^{1,0}_{\tau _L- T_1^0} \right] \ge \mathbb {E} \left[ C^{1,0}_{T_2^0 - T_1^0} \right] =\infty . \end{aligned}$$

In some special cases, Formula (26) can be used to obtain the first moment of $C^L_{\tau _L}$.

When $\gamma$ is zero, then for all $t \ge 0$, for all $k \in \llbracket 1, f_0 \rrbracket$ and for all $j \in \llbracket 1,N_k(\tau _L) \rrbracket$, $C^{k,j}_t = 1$. We deduce directly from Eq. (26) that

$$\begin{aligned} \mathbb {E}\left[ C^{L}_{\tau _L} \right] = f_0 + \sum _{k = 0}^{f_0 - 1} \mathbb {E} \left[ N_k(\tau _L) \right] . \end{aligned}$$

(27)

From Eq. (7), we have

$$\begin{aligned} \mathbb {E}\left[ N_k(\tau _L) \right]= & {} \mathbb {E}\left[ \mathcal {Y}_3 \left( \alpha _2 \int _{0}^{T_{k+1}} F^L_s ds \right) - \mathcal {Y}_3 \left( \alpha _2 \int _{0}^{T_{k}} F^L_s ds \right) \right] \\= & {} \mathbb {E}\left[ \mathcal {Y}_3 \left( \alpha _2 \int _{T_k}^{T_{k+1}} F^L_s ds \right) \right] = \mathbb {E}\left[ \alpha _2 \int _{T_k}^{T_{k+1}} F^L_s ds \right] , \end{aligned}$$

by Poisson process property. Since for all $t \in [T_k, T_{k+1})$, $F^L_t = f_0 - k$, we deduce that $\mathbb {E}\left[ N_k(\tau _L) \right] = \mathbb {E}\left[ \alpha _2 (f_0 - k)(T_{k+1} - T_k) \right]$. Using (4), we deduce that $\mathbb {E} \left[ N_k(\tau _L) \right] = \frac{\alpha _2(f_0 - k) }{\alpha _1(f_0 - k) } = \frac{\alpha _2}{\alpha _1 }$ and conclude with (27).

When $\alpha _2$ is zero, $N_k (t)$ is null for all $t \ge 0$, and we deduce directly from (26) that

$$\begin{aligned} \mathbb {E}\left[ C^{L}_{\tau _L} \right] = \sum _{k = 1}^{f_0} \mathbb {E} \left[ C^{k,0}_{\tau _L- T_k} \right] . \end{aligned}$$

(28)

Since $T_{f_0} = \tau _L$, we have $C^{f_0,0}_{\tau _L- T_{f_0}} = 1$. Let $k \in \llbracket 1, f_0 - 1 \rrbracket$. Since $\tau _L- T_k \overset{(law)}{=} \sum _{i = k + 1}^{f_0} \mathcal {E}\left( \alpha _1 (f_0 - i + 1)\right) \overset{(law)}{=} \sum _{i = 1}^{f_0 - k } \mathcal {E}\left( \alpha _1 i \right)$, using Proposition 1, we deduce that the density function of $\tau _L- T_k$ is

$$\begin{aligned} f_{\tau _L- T_k}(t) = \alpha _1 (f_0 - k) e^{- \alpha _1 t} (1 - e^{-\alpha _1 t})^{f_0 - k - 1}\mathbb {1}_{t \ge 0}. \end{aligned}$$

Then, conditioning $C^{k,0}_{\tau _L- T_k}$ on the law of $\tau _L- T_k$, we first deduce that

$$\begin{aligned} \displaystyle \mathbb {E} \left[ C^{k,0}_{\tau _L- T_k} \right] = \int _{0}^{+ \infty } \mathbb {E} \left[ C^{k,0}_{t} \right] f_{\tau _L- T_k}(t) dt, \end{aligned}$$

Then, since $\mathbb {E} \left[ C^{k,0}_{t} \right] = e^{\gamma t}$, we have, similarly as in Eq. (25),

$$\begin{aligned} \mathbb {E} \left[ C^{k,0}_{\tau _L- T_k} \right] = \frac{(f_0-k)!}{\left( (f_0-k)-\frac{\gamma }{\alpha _1}\right) !}, \end{aligned}$$

which ends the proof using (28). $\square$

The following proposition is analogous to Proposition 2, yet with the decoupled processes $\tilde{F}$ and $\tilde{C}$, whose moments are easier to estimate. Note that parameters $\tilde{\alpha },\tilde{\beta }, \tilde{\gamma }$ below are generic ones.

Proposition 6

Let $\tilde{F},\tilde{C}$ be independent pure-jump stochastic processes on $\mathbb N$, of infinitesimal generators

$$\begin{aligned} \overset{\sim }{\mathcal {L}}_F \phi (f)&= \tilde{\alpha } f \left[ \phi (f-1) - \phi (f) \right] , \\ \overset{\sim }{\mathcal {L}}_C \phi (c)&= \left[ \tilde{\beta } + \tilde{\gamma } c \right] \left[ \phi (c+1) - \phi (c) \right] . \end{aligned}$$

with deterministic initial condition $\tilde{F}(0)=f_0$ and $\tilde{C}(0)=n\ge 1$, and where $\tilde{\alpha },\tilde{\beta }, \tilde{\gamma }$ are non-negative rate parameters. Let

$$\begin{aligned} \tilde{\tau } = \inf \{ t>0; \quad \tilde{F}_{t} = 0 | f_0 \} \end{aligned}$$

For any $p\ge 1$,

$$\begin{aligned} \mathbb {E}\left[ (\tilde{C}_{\tilde{\tau }})^p \right] <\infty . \end{aligned}$$

(29)

if, and only if,

$$\begin{aligned} p \tilde{\gamma } < \tilde{\alpha }, \end{aligned}$$

(30)

Moreover, we have:

• if $\tilde{\gamma } >0$: for $p=1$,

  $$\begin{aligned} \mathbb {E}\left[ \tilde{C}_{\tilde{\tau }} \right] = n\frac{f_0!}{\left( f_0-\frac{\tilde{\gamma }}{\tilde{\alpha }}\right) !}+\frac{\tilde{\beta }}{\tilde{\gamma }} \left( \frac{f_0!}{\left( f_0-\frac{\tilde{\gamma }}{\tilde{\alpha }}\right) !}-1\right) , \end{aligned}$$

  and for $p=2$,

  $$\begin{aligned} \mathbb {E}\left[ (\tilde{C}_{\tilde{\tau }})^2 \right]= & {} \left( n+\frac{\tilde{\beta }}{\tilde{\gamma }}\right) \left( n+\frac{\tilde{\beta }}{\tilde{\gamma }}+1\right) \frac{f_0!}{\left( f_0-\frac{2\tilde{\gamma }}{\tilde{\alpha }}\right) !}\\&-\left( n+\frac{\tilde{\beta }}{\tilde{\gamma }}\right) \left( 1+2\frac{\tilde{\beta }}{\tilde{\gamma }}\right) \frac{f_0!}{\left( f_0-\frac{\tilde{\gamma }}{\tilde{\alpha }}\right) !}+\left( \frac{\tilde{\beta }}{\tilde{\gamma }}\right) ^2 \end{aligned}$$

• if $\tilde{\gamma } = 0$:

  $$\begin{aligned} \mathbb {E}\left[ \tilde{C}_{\tilde{\tau }} \right]= & {} n+\frac{\tilde{\beta }}{\tilde{\alpha }} \sum _{i = 1}^{f_0 } \frac{ 1}{i},\\ \mathbb {E}\left[ (\tilde{C}_{\tilde{\tau }})^2 \right]= & {} n+\frac{\tilde{\beta }}{\tilde{\alpha }} \sum _{i = 1}^{f_0 } \frac{ 1}{i}+\frac{\tilde{\beta }^2}{\tilde{\alpha }^2} \left( \sum _{i = 1}^{f_0 } \frac{ 1}{i^2}+\left( \sum _{i = 1}^{f_0 } \frac{ 1}{i}\right) ^2\right) \end{aligned}$$

Proof

Since $\tilde{\tau }$ and $\tilde{C}$ are independent, we deduce by conditioning on $\tilde{\tau }$ that

$$\begin{aligned} \mathbb {E}\left[ (\tilde{C}_{\tilde{\tau }})^p \right] = \displaystyle \int _{0}^{+ \infty }\mathbb {E}\left[ (\tilde{C}_{t})^p \right] f_{\tilde{\tau }}(t)dt, \end{aligned}$$

(31)

where $f_{\tilde{\tau }}$ is the density probability of $\tilde{\tau }$. Since $\tilde{F}$ is linear, we apply Proposition 1 and obtain

$$\begin{aligned} f_{\tilde{\tau }}(t) =\tilde{\alpha } f_0 e^{- \tilde{\alpha } t} (1 - e^{-\tilde{\alpha } t})^{f_0 - 1} \mathbb {1}_{[0, + \infty )}(t). \end{aligned}$$

(32)

Now, we suppose that $\tilde{\gamma } >0$. Then, $\tilde{C}$ can be decomposed as the independent sum of n Yule processes starting from 1 [see Eq. (5)] and a birth process with immigration (starting from 0). It is classical that the Yule process follows a geometric law of parameter $e^{-\tilde{\gamma } t}$, and the birth process with immigration follows a negative binomial law $\mathcal {BN}\left( \frac{\tilde{\beta }}{\tilde{\gamma }}, e^{- \tilde{\gamma } t} \right)$. Thus there exists $k,K>0$ (depending on model parameters, but independent of t) such that, for all $t \ge 0$,

$$\begin{aligned} ke^{p\tilde{\gamma } t}\le \mathbb {E}\left[ (\tilde{C}_{t})^p \right] \le Ke^{p\tilde{\gamma } t}. \end{aligned}$$

(33)

Combining Eq. (33) with Eqs. (31) and (32) yields (29). To obtain the remaining analytical formulas, we note that

$$\begin{aligned} \mathbb {E}\left[ \tilde{C}_{t} \right] = ne^{\tilde{\gamma } t}+\frac{\tilde{\beta }}{\tilde{\gamma }}(e^{\tilde{\gamma } t} - 1)=e^{\tilde{\gamma } t}\left( n+\frac{\tilde{\beta }}{\tilde{\gamma }}\right) -\frac{\tilde{\beta }}{\tilde{\gamma }}, \end{aligned}$$

(34)

and

$$\begin{aligned} \mathbb {E}\left[ (\tilde{C}_{t})^2 \right] = e^{2\tilde{\gamma } t}\left( n+\frac{\tilde{\beta }}{\tilde{\gamma }}\right) \left( n+\frac{\tilde{\beta }}{\tilde{\gamma }}+1\right) -e^{\tilde{\gamma } t}\left( n+\frac{\tilde{\beta }}{\tilde{\gamma }}\right) \left( 1+2\frac{\tilde{\beta }}{\tilde{\gamma }}\right) +\left( \frac{\tilde{\beta }}{\tilde{\gamma }}\right) ^2. \end{aligned}$$

(35)

Also, for any p such that (30) holds true, we have (with the change of variables $x=1-e^{-\tilde{\alpha } t}$)

$$\begin{aligned} \int _0^\infty e^{p\tilde{\gamma } t}f_{\tilde{\tau }}(t)dt=f_0\int _0^1 (1-x)^{-\frac{p\tilde{\gamma }}{\tilde{\alpha }}}x^{f_0-1}dx=f_0B\left( f_0,1-\frac{p\tilde{\gamma }}{\tilde{\alpha }}\right) , \end{aligned}$$

where B is the standard Beta function. We deduce that

$$\begin{aligned} \int _0^\infty e^{p\tilde{\gamma } t}f_{\tilde{\tau }}(t)dt=\frac{f_0!}{\left( f_0-\frac{p\tilde{\gamma }}{\tilde{\alpha }}\right) !}, \end{aligned}$$

where we use the notation $\left( m-x\right) !=\prod _{k=1}^m (k-x)$. Then, using Eqs. (34)-(35) and (32), we deduce from (31) that

$$\begin{aligned} \mathbb {E}\left[ \tilde{C}_{\tilde{\tau }} \right] = n\frac{f_0!}{\left( f_0-\frac{\tilde{\gamma }}{\tilde{\alpha }}\right) !}+\frac{\tilde{\beta }}{\tilde{\gamma }} \left( \frac{f_0!}{\left( f_0-\frac{\tilde{\gamma }}{\tilde{\alpha }}\right) !}-1\right) \end{aligned}$$

and

$$\begin{aligned} \mathbb {E}\left[ (\tilde{C}_{\tilde{\tau }})^2 \right]= & {} \left( n+\frac{\tilde{\beta }}{\tilde{\gamma }}\right) \left( n+\frac{\tilde{\beta }}{\tilde{\gamma }}+1\right) \frac{f_0!}{\left( f_0-\frac{2\tilde{\gamma }}{\tilde{\alpha }}\right) !}\\&-\left( n+\frac{\tilde{\beta }}{\tilde{\gamma }}\right) \left( 1+2\frac{\tilde{\beta }}{\tilde{\gamma }}\right) \frac{f_0!}{\left( f_0-\frac{\tilde{\gamma }}{\tilde{\alpha }}\right) !}+\left( \frac{\tilde{\beta }}{\tilde{\gamma }}\right) ^2 \end{aligned}$$

If $\tilde{\gamma } = 0$, then $\tilde{C}$ is a pure immigration process starting from n, and follows a shifted Poisson law $n+\mathcal {P}\left( \tilde{\beta } t \right)$ at time $t \ge 0$. Using the same approach, we obtain that

$$\begin{aligned} \displaystyle \mathbb {E}\left[ \tilde{C}_{\tilde{\tau }} \right] = \int _{0}^{+ \infty } (n+\tilde{\beta } t) f_{\tilde{\tau }}(t) dt = n+\tilde{\beta } \mathbb {E}\left[ \tilde{\tau }\right] = n+\frac{\tilde{\beta }}{\tilde{\alpha }} \sum _{i = 1}^{f_0 } \frac{ 1}{i}, \end{aligned}$$

and

$$\begin{aligned} \displaystyle \mathbb {E}\left[ (\tilde{C}_{\tilde{\tau }} )^2\right]= & {} \int _{0}^{+ \infty } (n+\tilde{\beta } t(\tilde{\beta } t+1)) f_{\tilde{\tau }}(t) dt = n+\tilde{\beta } \mathbb {E}\left[ \tilde{\tau }\right] +\tilde{\beta }^2 \mathbb {E}\left[ (\tilde{\tau })^2\right] \\= & {} n+\frac{\tilde{\beta }}{\tilde{\alpha }} \sum _{i = 1}^{f_0 } \frac{ 1}{i}+\frac{\tilde{\beta }^2}{ \tilde{\alpha }^2} \left( \sum _{i = 1}^{f_0 } \frac{ 1}{i^2}+\left( \sum _{i = 1}^{f_0 } \frac{ 1}{i}\right) ^2\right) , \end{aligned}$$

. $\square$

1.4 Numerical scheme for $\mathbb {E}[\tau ]$ and $\mathbb {E}[C_{\tau }]$

We design Algorithm 1 to compute a numerical estimate of $g(f_0,0)$, solution of Eq. (13) that represents either $\mathbb {E}\left[ \tau \right]$ or $\mathbb {E}\left[ C_{\tau }\right]$ according to the specific choice of boundary condition. This algorithm requires $\gamma <\alpha _1+\beta$ to compute $\mathbb {E}\left[ \tau \right]$, and $2\gamma <\alpha _1+\beta$ to compute $\mathbb {E}\left[ C_{\tau }\right]$, in agreement with Theorem 1, Proposition 3 and Proposition 4. The prefactor A given below is obtained thanks to Proposition 6.

1.5 In silico dataset

We generate in silico datasets to further explore parameter identifiability. For each submodel, we choose two different parameter sets with contrasted values in the division rates $\alpha _2$ or $\gamma$ and/or transition rate $\beta$. The parameter values are summarized in Table 2. We obtain the corresponding 10 datasets by simulating 1000 trajectories from the SDE (1), with the Gillespie algorithm (Gillespie 1976), starting from the initial condition $(F_0,0)$ at time $t=0$ up to the time when $C(t) = 31$ (the value $C(t) = 31$ corresponds to the maximal number of cuboidal cells observed in the experimental dataset). The initial random variable $F_0$ follows a truncated Poisson law of parameter $\mu$ [see Eq. (17)]. For each trajectory, we select uniformly randomly one point (f, c) among the state space points reached by the trajectory, so that each in silico datasets is composed of $N=1000$ points. This way of sampling, letting to time-free and uncoupled datapoints, mimics the experimental protocol.

Table 2 Parameter sets used to generate the in silico datasets

1.6 Detailed fitting procedure

1.6.1 Maximum likelihood estimator

For each submodel and dataset, the optimal parameter values are given by the MLE $\hat{\theta } = \left( \widehat{\beta } , \widehat{\alpha _2} , \widehat{\gamma }, \widehat{\mu } \right)$, which we compute by minimizing the negative log-likelihood,

$$\begin{aligned} \hat{\theta } := \arg \min _{\theta \in \varTheta } \left( - \log \left( \mathcal {L}(\mathbf {x};\theta ) \right) \right) , \end{aligned}$$

for a dataset $\mathbf {x}$ and where $\varTheta$ is constructed by fixing all parameters related to the nonpresent events to the singleton $\{0\}$: for instance, in submodel $(\mathcal {R}_1,\mathcal {R}_4)$, we have $\varTheta = \{0\} \times \{0\} \times \mathbb {R}_+ \times [1, + \infty )$.

To compute the minimum, we use a derivative-free optimization algorithm: the Differential Evolution (DE) algorithm (Storn and Price 1997). In the following, we describe the whole procedure for the complete model $(\mathcal {R}_1,\mathcal {R}_2,\mathcal {R}_3,\mathcal {R}_4)$. The algorithm starts from an initial population in which each individual is represented by a set of real numbers $(\beta , \alpha _2, \gamma , \mu )$. Then, the population evolves along successive generations by mutation and recombination processes. At each generation, the likelihood function is used to assess the fitness of the individuals, and only the best individuals are kept in the population. We have set the intrinsic optimization parameters as follows: the initial population has a size of 20 individuals, and the probability of mutation and crossing-over equals to 0.8 and 0.7 respectively. The starting individual parameter sets are defined on a log scale, and drawn from a uniform distribution on $\varTheta = [-6,6]^3 \times [0, 1.5]$. The algorithm was run over 1,000 iterations.

Table 3 Size-step used for each parameter in the PLE estimate, in log-scale, within each submodel and each dataset

1.6.2 Profile likelihood estimate

For each ith component of the MLE $\hat{\theta }_i$, $i \in \llbracket 1, 4 \rrbracket$, we compute a vector $\hat{\theta }|[\theta _{i} = x]$ on a grid $G_i$ around the MLE $\hat{\theta }$, with $x \in G_i$:

$$\begin{aligned} \hat{\theta }| [\theta _{i} = x] := \arg \min _{\theta \in \varTheta , \theta _{i} = x} \left( - \log \left( \mathcal {L}(\mathbf {x};\theta ) \right) \right) , \end{aligned}$$

and its associated PLE (vector) $\mathcal {L}(\mathbf {x};\hat{\theta }|\theta _{i})$. We design the grid $G_i$ around the MLE $\hat{\theta }_{i}$ with a fixed step size (see Table 3 for details), and re-optimize the remaining parameters using the DE algorithm with the same optimization parameters (mut = 0.8, crossp = 0.7, popsize = 20, its = 1000) and initial parameter sets defined on a log scale, and drawn from a uniform distribution on $[-6,6]^3$ for parameters $\beta$, $\alpha _2$ and $\gamma$, and on $[-1 + \log (\hat{\mu }), \log (\hat{\mu }) + 1]$ for parameter $\mu$.

1.6.3 Confidence intervals

Pointwise likelihood-based confidence intervals are constructed thanks to the likelihood ratio test, following Raue et al. (2009); for each estimated parameter $\hat{\theta }_{i}$, we select all the parameters $\theta _{i} = x$ such that:

$$\begin{aligned} \mathcal {L}(\mathbf {x};\theta |[\theta _{i} =x]) - \mathcal {L}(x;\hat{\theta }) < 0.5 * \varDelta _{\alpha } , \end{aligned}$$

where $\varDelta _{0.95} = \chi ^2(0.95, 1) = 3.84$ is the 0.95-quantile of the $\chi ^2$ law with 1 degree of freedom.

Fig. 10

Two-event submodels: Best fit trajectories for in silico datasets. Using Eqs. (15)–(17), we compute each probability $\mathbb {P}\left[ F_c = f\right]$ for submodel $(\mathcal {R}_1, \mathcal {R}_4)$ (left panel) and $(\mathcal {R}_1, \mathcal {R}_3)$ (right panel) with their respective MLE parameter set associated with the in silico dataset 1. Each dark gray square corresponds to a data point. The colormap corresponds to the probability values $\mathbb {P}\left[ F_c = f\right]$ in log10 scale (color figure online)

Fig. 11

Two-event submodels: PLE for in silico datasets. Each panel represents the PLE, in log10 scale, obtained from the in silico datasets, and either submodel $(\mathcal {R}_1,\mathcal {R}_4)$ (left panels) or $(\mathcal {R}_1,\mathcal {R}_3)$ (right panels). The dashed black line represents the 95%-statistical threshold. Orange solid lines: PLE values for the initial condition parameter $\mu$; blue solid lines: PLE values for the symmetric cell proliferation rate $\gamma$; green solid lines: PLE values for the asymmetric cell division rate $\alpha _2$. The colored points represent the associated MLE, and the star symbols are the expected (true) parameter values (see Table 2) (color figure online)

Fig. 12

Three-event submodels: PLE. Each panel represents the PLE, in log10 scale, obtained from the experimental (top panels) and in silico datasets (bottom panels), and either submodel $(\mathcal {R}_1,\mathcal {R}_2,\mathcal {R}_4)$ (left panels), $(\mathcal {R}_1,\mathcal {R}_2,\mathcal {R}_3)$ (center panels), $(\mathcal {R}_1, \mathcal {R}_3, \mathcal {R}_4)$ (right panels). The dashed black line represents the 95%-statistical threshold. Orange solid lines: PLE values for the initial condition parameter $\mu$; blue solid lines: PLE values for the symmetric cell proliferation rate $\gamma$; green solid lines: PLE values for the asymmetric cell division rate $\alpha _2$; red solid lines: PLE values for the self-amplification transition rate $\beta$. The colored points represent the associated MLE, and (in the bottom panels) the star symbols are the expected (true) parameter values (see Table 2) (color figure online)

1.6.4 Model selection

AIC and BIC analyses were performed to compare the submodels. The reader can refer to Burnham and Anderson (2003) (Chapter 6) for a detailed presentation of the rule of thumb, classically used to analyze the $\varDelta ^{AIC}_i := AIC_i - AIC_{\min }$ and $\varDelta ^{BIC}_i = BIC_i - BIC_{\min }$ values, where i is the index of the ith model:

• a $\varDelta$ value lower than 2 indicates that the considered model is almost as probable as the “best” model;

• a $\varDelta$ value between 2 and 7 suggests that the considered model is a suitable alternative to the “best” model;

• a $\varDelta$ value between 7 and 10 suggests that the considered model is less relevant than the “best” model;

• a $\varDelta$ value upper than 10 suggests that the considered model can be safely ruled out.

This $\varDelta$ approach is completed by the AIC and BIC weight analyses. For each dataset and criterion (AIC or BIC), we order the AIC/BIC weights from the highest to the lowest values. We then compute the cumulative sum of these weights, starting from the highest one. The selected models are the first ones such that the cumulative sum reaches the threshold p-value 0.95.

1.7 Detailed calibration analysis

1.7.1 Two-event submodels

The fitting results obtained for submodels $(\mathcal {R}_1,\mathcal {R}_3)$ and $(\mathcal {R}_1,\mathcal {R}_4)$ from the experimental datasets are shown in Fig. 5 and discussed in the main text, Sect. 4.3. One fitting result for the in silico datasets and for submodels $(\mathcal {R}_1,\mathcal {R}_3)$ and $(\mathcal {R}_1,\mathcal {R}_4)$ is shown in Fig. 10. We verify that the inferred trajectories are coherent with the selected datasets.

In Fig. 11, we show the PLE for each estimated parameter in each in-silico dataset. Both the initial condition parameter $\mu$ (orange solid lines) and asymmetric division rate $\alpha _2$ (green solid line) are practically identifiable [in the sense given in Raue et al. (2009)], while parameter $\gamma$ (blue solid line) is only partially practically identifiable in most cases. We observe that both parameters $\alpha _2$ ($\mathcal {R}_3$) and $\gamma$ ($\mathcal {R}_4$) are practically identifiable and close to their expected values (less than one log10 of difference) when the parameters are of the same order of magnitude than $\alpha _1$. In contrast, a small parameter value compared to $\alpha _1$ leads to a biased parameter estimate, with a huge shift between the estimated and true parameter values (up to two log10 difference).

The estimator for the initial condition parameter $\mu$ may also be slightly biased with submodel $(\mathcal {R}_1,\mathcal {R}_3)$ (less than one log10 of difference) compared to submodel $(\mathcal {R}_1,\mathcal {R}_4)$ .

1.7.2 Three-event submodels and complete model

We turn now to the analysis of three-event submodels $(\mathcal {R}_1,\mathcal {R}_2,\mathcal {R}_3)$, $(\mathcal {R}_1,\mathcal {R}_2,\mathcal {R}_4)$ and $(\mathcal {R}_1,\mathcal {R}_3,\mathcal {R}_4)$) and the complete model ($(\mathcal {R}_1,\mathcal {R}_2,\mathcal {R}_3,\mathcal {R}_4)$. Qualitatively, the fitting results for submodel $(\mathcal {R}_1,\mathcal {R}_2,\mathcal {R}_3)$ are similar to those for submodel $(\mathcal {R}_1,\mathcal {R}_3)$ (data not-shown); they are characterized by a high probability to produce ten or more proliferative cells before the precursor cell extinction. The fitting results for submodels $(\mathcal {R}_1,\mathcal {R}_2,\mathcal {R}_4)$ and $(\mathcal {R}_1,\mathcal {R}_3,\mathcal {R}_4)$ are rather similar to submodel $(\mathcal {R}_1,\mathcal {R}_4)$; they are characterized by direct cell transition with very little concomitant cell proliferation, followed by prolonged cell proliferation after precursor cell extinction. The fitting results for the complete model are shown in the bottom panels of Fig. 5 for both the Wild-type and Mutant subsets and discussed in the main text, Sect. 4.3.

The PLEs for each dataset and each parameter are presented in Fig. 12 for the three-event submodels. The corresponding parameter values and confidence intervals for the Wild-Type and Mutant subsets are given in Tables 4 and 5. As observed for the two-event submodels, in each case, the initial condition parameter $\mu$ (orange solid lines) is always practically identifiable, and its fitted value is close to the true one for the in silico datasets. In contrast, all other parameters have a lack of identifiability, both with the experimental and in silico datasets. Specifically, the asymmetric division rate $\alpha _2$ is practically not identifiable for submodel $(\mathcal {R}_1,\mathcal {R}_2,\mathcal {R}_3)$ with the experimental subsets. Interestingly, when the asymmetric division event is combined with the symmetric division event (submodel $(\mathcal {R}_1,\mathcal {R}_3,\mathcal {R}_4)$) rather than with the auto-amplified transition (submodel $(\mathcal {R}_1,\mathcal {R}_2,\mathcal {R}_3)$), the asymmetric division rate $\alpha _2$ becomes identifiable in the experimental subsets, which reveals complex parameter dependencies between the asymmetric division rate $\alpha _2$ and auto-amplified transition rate $\beta$.

Table 4 Wild-type MLE parameter sets

Table 5 Mutant parameter sets

Fig. 13

Proliferation versus transition. For the Wild-Type (left panel) and Mutant (right panel) datasets, and for submodel $(\mathcal {R}_1,\mathcal {R}_2,\mathcal {R}_4)$ and complete model $(\mathcal {R}_1,\mathcal {R}_2,\mathcal {R}_3,\mathcal {R}_4)$, we represent in colored lines both the optimal value of self-amplification transition rate $\beta$ along the PLE of the symmetric cell proliferation rate $\gamma$, and the optimal value of the symmetric cell proliferation rate $\gamma$ along the PLE of self-amplification transition rate $\beta$. The black dashed line represents the straight line $\gamma =\beta +\alpha _1=\beta +1$ (color figure online)