Cooperative metabolic resource allocation in spatially-structured systems

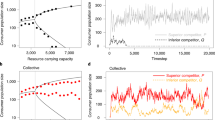
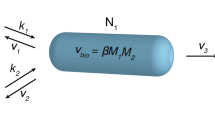
Abstract

Natural selection has shaped the evolution of cells and multi-cellular organisms such that social cooperation can often be preferred over an individualistic approach to metabolic regulation. This paper extends a framework for dynamic metabolic resource allocation based on the maximum entropy principle to spatiotemporal models of metabolism with cooperation. Much like the maximum entropy principle encapsulates ‘bet-hedging’ behaviour displayed by organisms dealing with future uncertainty in a fluctuating environment, its cooperative extension describes how individuals adapt their metabolic resource allocation strategy to further accommodate limited knowledge about the welfare of others within a community. The resulting theory explains why local regulation of metabolic cross-feeding can fulfil a community-wide metabolic objective if individuals take into consideration an ensemble measure of total population performance as the only form of global information. The latter is likely supplied by quorum sensing in microbial systems or signalling molecules such as hormones in multi-cellular eukaryotic organisms.

Appendix A: Derivation of the cooperative control law

Collecting dynamic variables into vectors ${\mathbf {X}}_i = ({\mathbf {m}}_i,x_i)^T$, the system (4) can be represented by the coupled equations $\dot{{\mathbf {X}}}_i = {\mathbf {F}}_i({\mathbf {X}}, {\mathbf {u}}^i)$ ($i=1,2,\ldots ,{\mathcal {N}}$) with ${\mathbf {X}} = ({\mathbf {X}}_1, {\mathbf {X}}_2, \ldots , {\mathbf {X}}_{{\mathcal {N}}})^T$. As in Young and Ramkrishna (2007), Tourigny (2020), the individual controls ${\mathbf {u}}^i$ are determined by using the linearisation of (4) about the state ${\mathbf {X}}(t)$ and reference controls $\{ {\mathbf {u}}^i_0 \}_{i=1,2,\ldots ,{\mathcal {N}}}$ as a good approximation for the system response at time $t+\tau$ with $\tau \in [0,\Delta t]$. The linearised equations are

$$\begin{aligned} \frac{d}{d\tau } \Delta {\mathbf {X}}_i = {\mathbf {A}}_i \Delta {\mathbf {X}} + {\mathbf {B}}_i \Delta {\mathbf {u}}^i + {\mathbf {F}}_i({\mathbf {X}}(t),{\mathbf {u}}^i_0) \end{aligned}$$

where

$$\begin{aligned} {\mathbf {A}}_i = \frac{\partial }{\partial {\mathbf {X}}} {\mathbf {F}}_i ({\mathbf {X}}(t),{\mathbf {u}}^i) \end{aligned}$$

is the ith block row of the full Jacobian matrix ${\mathbf {A}}$ and

$$\begin{aligned} {\mathbf {B}}_i = \frac{\partial }{\partial {\mathbf {u}}^i} {\mathbf {F}}_i ({\mathbf {X}}(t),{\mathbf {u}}^i), \end{aligned}$$

with $\Delta {\mathbf {X}} = {\mathbf {X}}(t+\tau ) - {\mathbf {X}}(t)$ and $\Delta {\mathbf {u}}^i = {\mathbf {u}}^i (t+ \tau ) - {\mathbf {u}}^i_0$. When the species at all nodes are identical (i.e., ${\mathbf {S}}_i = {\mathbf {S}}$, $K_i = K$, ${\mathbf {c}}_i = {\mathbf {c}}$, $r^i_k = r_k$, and ${\mathbf {Z}}^k_i = {\mathbf {Z}}^k$ for all $i = 1,2,\ldots , {\mathcal {N}}$) then each cooperative maximum entropy control ${\mathbf {u}}^i$ is obtained by maximising the objective functional

$$\begin{aligned} {\mathcal {F}}_i({\mathbf {u}}) = \varvec{\lambda }^T_i {\mathbf {B}}_i {\mathbf {u}} + \sigma H({\mathbf {u}}) \end{aligned}$$

with respect to ${\mathbf {u}}$, where

$$\begin{aligned} H({\mathbf {u}} ) = - \sum _{k=1}^K u_k \log (u_k) \end{aligned}$$

is the entropy constraint and $\varvec{\lambda } = (\varvec{\lambda }_1,\varvec{\lambda }_2,\ldots ,\varvec{\lambda }_{{\mathcal {N}}})^T$ is the ${\mathcal {N}} \times (M+1)$-dimensional vector of Pontryagin co-state variables obtained by solving the boundary value problem

$$\begin{aligned} - \frac{d}{d \tau } \varvec{\lambda } = {\mathbf {A}}^T \varvec{\lambda }, \quad \varvec{\lambda }(t + \Delta t) = {\mathbf {q}}_i . \end{aligned}$$

The complete solution to the co-state equations is

$$\begin{aligned} \varvec{\lambda } (t + \tau ) = {\mathbf {e}}^{{\mathbf {A}}^T(\Delta t - \tau )} {\mathbf {q}}_i, \quad 0 \le \tau \le \Delta t , \end{aligned}$$

but the effective return-on-investment (6) is obtained by substituting for $\varvec{\lambda }$ with the heuristic $\tau =0$ because, ultimately, only the optimal control input at the current time t is of interest (Young and Ramkrishna 2007). Maximisation of ${\mathcal {F}}_i$ proceeds as in Tourigny (2020) to yield the cooperative maximum entropy control (7).

An expression for the greedy effective return-on-investment is obtained by setting $\Delta t = 0$, in which case $\varvec{\lambda }_i = \partial \phi _i ({\mathbf {X}})/\partial {\mathbf {X}}_i$. Moreover, $\partial \phi _i/\partial x_i$ is the only non-zero component of this vector because the cooperative objective $\phi _i$ does not depend on concentrations of slow metabolites. Differentiation of the generalised mean $\phi _i = M_p({\mathbf {x}})$ with respect to $x_i$ yields

$$\begin{aligned} \frac{\partial \phi _i}{\partial x_i} = \frac{x^{p-1}_i}{\sum _{j=1}^{\mathcal {N}} x_j^p} \cdot \left( \frac{1}{{\mathcal {N}}} \sum _{j=1}^{\mathcal {N}} x_j^p \right) ^{1/p} = \frac{x_i^{p-1}}{x_i^p + y^p} \cdot M_p({\mathbf {x}}) \end{aligned}$$

and the kth column of ${\mathbf {B}}_i$ is

$$\begin{aligned} {\mathbf {B}}_i^k = x_i r_k({\mathbf {m}}_i) \begin{pmatrix} {\mathbf {S}} \\ {\mathbf {c}}^T \end{pmatrix} {\mathbf {Z}}^k \end{aligned}$$

so that

$$\begin{aligned} {\mathcal {R}}^{k,i}_0 = \frac{x_i^p}{x_i^p + y^p} \cdot M_p({\mathbf {x}}) \cdot r_k({\mathbf {m}}_i) {\mathbf {c}}^T {\mathbf {Z}}^k . \end{aligned}$$

This provides the greedy effective return-on-investment (8) defined using $R^k_0({\mathbf {m}}_i)$ in the main text, and the resulting greedy cooperative maximum entropy control is

$$\begin{aligned} u^i_k(t) = \frac{1}{Q_i}\exp \left( {\mathcal {R}}_0^{k,i} /\sigma \right) , \quad k=1,2, \ldots ,K \end{aligned}$$

with $Q_i = \sum _{k=1}^K \exp ( {\mathcal {R}}_0^{k,i} /\sigma )$. As mentioned in the main text, alternative controls can be obtained in cases where the objectives $\phi _i$ and/or species are different across nodes in the population network, but are not considered here. To demonstrate the utilitarian objective with $p=1$ recovers the individualistic greedy maximum entropy control law from Tourigny (2020), note that in this case

$$\begin{aligned} M_1({\mathbf {x}}) = \frac{1}{{\mathcal {N}}} \sum _{j=1}^{\mathcal {N}} x_j , \quad x_i^1 + y^1 = x_i + \sum _{j \ne i }^{\mathcal {N}} x_j = \sum _{j=1}^{\mathcal {N}} x_j \end{aligned}$$

so that substitution for the denominator in ${\mathcal {R}}^{k,i}_0$ yields

$$\begin{aligned} {\mathcal {R}}^{k,i}_0 = \frac{1}{{\mathcal {N}}} \cdot x_i r_k({\mathbf {m}}_i) {\mathbf {c}}^T {\mathbf {Z}}^k , \end{aligned}$$

which is the individualistic effective return-on-investment (Equation 18 in Tourigny 2020) for the kth EFM at node i, multiplied by a common factor of $1/{\mathcal {N}}$ that has no effect on the resulting control law.

Although beyond the scope of this paper, it is worth pointing out that use of the maximum entropy principle in Tourigny (2020) and its cooperative extension considered here is of a slightly different nature compared to those discussed previously (De Martino et al. 2017; Fernandez-de-Cossio-Diaz and Mulet 2019) (see also Fleming et al. (2012) for explicit use of entropy in an objective function) because the Boltzmann-like distribution is used to weight EFMs rather than individual reactions. The resulting steady state flux distributions obtained using these approaches are not necessarily the same, since the former maximum entropy principle will emphasise the spread of resource across EFMs while the latter does so on a reaction-by-reaction basis. At least in a simplified case where effective return-on-investment is not considered and only stoichiometric constraints must be satisfied, it could be argued the former is more biologically-relevant because spreading resource equally among metabolic pathways– as fundamental functional units of the cell– would be more meaningful than equal distribution of resource among reactions. The latter, albeit done under stoichiometric constraints, could result in metabolic pathways containing more reactions receiving a greater fraction of resource even though their effective return-on-investments are no larger than others.