Abstract
Let U be a bounded open connected set in \(\mathbb {R}^n\) (\(n\ge 1\)). We refer to the unique weak solution of the Poisson problem \(-\Delta u = \chi _A\) on U with Dirichlet boundary conditions as \(u_A\) for any measurable set A in U. The function \(\psi :=u_U\) is the torsion function of U. Let V be the measure \(V:=\psi \,\mathscr {L}^n\) on U where \(\mathscr {L}^n\) stands for n-dimensional Lebesgue measure. We study the variational problem
with \(p\in (0,1)\) where \(J(A):=\int _Au_A\,dx\) and the supremum is taken over measurable sets \(A\subset U\) subject to the constraint \(V(A)=pV(U)\). We relate the above problem to an unstable two-phase membrane problem. We characterise optimsers in the case \(n=1\). The proof makes use of weighted isoperimetric and Pólya–Szegö inequalities.
Similar content being viewed by others
1 Introduction and Motivation
Let U be a bounded open connected set in \(\mathbb {R}^n\) (\(n\ge 1\)). We refer to the unique weak solution of the Poisson problem
as \(u_A\) for any measurable set A in U. The function \(\psi :=u_U\) is the torsion function of U. Let V be the measure \(V:=\psi \,\mathscr {L}^n\) on U where \(\mathscr {L}^n\) stands for the n-dimensional Lebesgue measure. For \(p\in (0,1)\) consider the variational problem
where \(J(A):=(u_A,\chi _A)\) and the supremum is taken over measurable sets \(A\subset U\) subject to the constraint \(V(A)=pV(U)\). Here, \((\cdot ,\cdot )\) stands for the usual inner product in the real Hilbert space \(L^2(U)\). Any maximiser E in (1.2) will be called an optimal configuration for the data (U, p). If E is an optimal configuration and \(u=u_E\), then (u, E) will be called an optimal pair.
In Corollary 2.2 we show that for each \(p\in (0,1)\) the problem (1.2) admits an optimal pair (u, E) for the data (U, p). In Proposition 3.3 we characterise the optimal configuration E as a super level set of \(u/\psi \); that is, \(E=\{u>c\psi \}\) for some \(c\in (0,1)\) up to \(\mathscr {L}^n\)-a.e. equivalence. The derivation assumes that U is a \(C^{1,1}\) domain. Under this last assumption, we show in Corollary 3.4 that u satisfies the following semi-linear elliptic partial differential equation with discontinuous nonlinearity. Put \(v:=u-c\psi \) with c as above. Then v is a strong solution of the problem
where \(\Omega _\pm (v):=\{\pm v>0\}\). The above equation is similar to Problem C (the two-phase membrane problem) in [20, 1.2.3] but with a sign change; see also the unstable membrane problem [20] 2.5. It is noted in [20, 1.1.7] that the composite membrane problem (see [6, 7]) is akin to the unstable membrane problem. Our terminology is adopted from [6, 7] and in places there is a similarity in method. The regular part of the free boundary \(\Gamma (v)=\partial \Omega _\pm (v)\cap U\) is real-analytic (Theorem 3.7). In Sect. 4 we replace U with the unit ball B in \(\mathbb {R}^n\) (\(n\ge 2\)). For \(p\in (0,1)\) we show that any optimal configuration E for the data (B, p) possesses spherical cap symmetry \(\mathscr {L}^n\)-a.e. (see Theorem 4.1).
In the remainder of the article, we study the problem (1.2) in the one-dimensional case \(n=1\) and take \(B=(-1,1)\). In Theorem 9.5 we show that any optimal configuration E with data (B, p) is \(\mathscr {L}^1\)-a.e. equivalent to an open interval abutting a boundary point of B. A first step in obtaining this result is to transform the problem using an analog of the ground-state transformation (with the torsion function in place of the ground-state) (see Proposition 9.2). We then obtain an isoperimetric inequality on B with volume density \(\psi \) and perimeter density \(\psi ^{3/2}\) (Theorem 6.3) and a corresponding Hardy-Littlewood type inequality (Theorem 6.6) and a Pólya–Szegö inequality (Theorem 7.10). We also study the case of equality in the isoperimetric and Pólya–Szegö inequalities (Theorem 6.4 and Corollary 8.7 respectively). We have been guided by [2] in obtaining these results, though our setting and proofs are slightly different.
We have not obtained an analog of Theorem 9.5 in the case \(n\ge 2\). At least part of our method transfers to higher dimensions. There is a counterpart of the isoperimetric inequality Theorem 6.3 (though its derivation is more involved with the usual difficulties around regularity and stability) and the Hardy–Littlewood inequality is a ready consequence. A potential stumbling block is the validity of a corresponding Pólya–Szegö inequality. We note that the sufficient conditons given in [22] are stringent.
The problem (1.2) is related to maximum flux exchange flow (a model of magma flow in a volcanic vent [15]). We take \(n=2\) and consider a configuration of two immiscible fluids in a vertical duct with cross-section U in a state of steady flow. The densities of the fluids are labelled \(\rho \), \(\rho ^\prime \) with \(\rho > \rho ^\prime \) and each fluid has unit viscosity. The pressure p has constant gradient \(\partial p/\partial z = -G\) on U. Suppose the fluid with density \(\rho \) occupies a region A in U. By the Navier–Stokes equations, the vertical component of velocity u satisfies
Dirichlet boundary conditions are imposed on the boundary of U and it is assumed that u and its gradient are continuous on the interface between the two regions A and \(U\setminus A\).
The parameter G lies in the interval \((\rho ^\prime g,\rho g)\) which allows the possibility of bidirectional flow. On rescaling (and relabelling the velocities) we obtain the system
where
is a proxy for the pressure gradient. Two problems arise: one to maximise the flux \((\chi _{U\setminus A},u)\) over regions A which satisfy the flux balance condition \((u,1) = 0\) with constant \(\lambda \); the other in which we optimize also over \(\lambda \). In detail,
where in the latter \(\lambda \) is fixed in the interval \((-1,1)\). In the case \(n=1\) and \(U=B\) we show that any optimal configuration E for the problem (1.5) with data \((B,\lambda )\) is \(\mathscr {L}^1\)-a.e. equivalent to an open interval abutting a boundary point of B in Theorem 9.8. Moreover, any optimal configuration E for the problem (1.4) is \(\mathscr {L}^1\)-a.e. equivalent to either \((-1,0)\) or (0, 1).
2 Existence of Optimal Configurations
Define
for \(t\in (0,V(U))\) and consider the variational problem
where \(J(f):=(u_f,f)\) and \(u_f\) is the unique solution of the Poisson problem (1.1) but with inhomogeneity f. The first main result runs as follows.
Theorem 2.1
Fix \(t\in (0,V(U))\). Then
-
(i)
there exists \(f\in \mathscr {V}_t\) such that \(\beta (U,t) = J(f)\);
-
(ii)
\((\psi ,f)=t\);
-
(iii)
f has the form \(f=\chi _E\) for some measurable set E in U.
Corollary 2.2
For each \(p\in (0,1)\) the problem (1.2) admits an optimal pair (u, E) for the data (U, p).
Proof
Let \(p\in (0,1)\) and put \(t:=p V(U)\). Let E be as in Theorem 2.1 (iii). Then \(V(E)=(\psi ,\chi _E)=t=pV(U)\). Let \(A\subset U\) be a measurable set with \(V(A)=pV(U)\). Then \(f=\chi _A\in \mathscr {V}_t\) so \(J(E)\ge J(A)\). \(\square \)
We prepare a few lemmas before proving Theorem 2.1.
Lemma 2.3
Let X, Y be (real) Banach spaces and suppose that \(X\subset Y\) with continuous embedding. Let \((x_h)\) be a sequence in X which converges weakly in X to \(x\in X\). Then \((x_h)\) converges weakly to x in Y.
Proof
Note that for any \(g\in Y^\prime \), \(g\vert _X\in X^\prime \). \(\square \)
We remark that the Dirichlet Laplacian \((D(\Delta ),\,\Delta )\) is associated with the Dirichlet form \((\mathscr {F},\,\mathscr {E})\) in \(L^2(U)\) with form domain \(\mathscr {F}:=W^{1,2}_0(U)\) and

Let G stand for the corresponding Green operator.
Lemma 2.4
Let \(t\in (0,V(U))\). Then
-
(i)
the functional \(J:\,\mathscr {V}_t\rightarrow \mathbb {R}\) is continuous in the topology of weak sequential convergence;
-
(ii)
\(J:\,\mathscr {V}_t\rightarrow \mathbb {R}\) is convex.
Proof
(i) Suppose that a sequence \((f_h)\) in \(\mathscr {V}_t\) converges weakly to an element \(f\in \mathscr {V}_t\) in \(L^2(U)\). Put \(u_h:=G f_h\in L^2(U)\). For each h and \(\varphi \in L^2(U)\),
by symmetry of G so that \((u_h,\,\varphi )\rightarrow (f,\,G\varphi )= (u,\,\varphi )\) as \(h\rightarrow \infty \) where \(u:=Gf\). We also have that
for any \(\varphi \in \mathscr {F}\). This means that \((u_h)\) converges weakly to u in \(\mathscr {F}\).
Note that \(W^{1,2}_0(U)\subset W^{1,1}_0(U)\) and \(\Vert u\Vert _{W^{1,1}_0(U)}\le \sqrt{2\,|U|}\,\Vert u\Vert _{W^{1,2}_0(U)}\) for each \(u\in W^{1,2}_0(U)\). By Lemma 2.3, \((u_h)\) converges weakly to u in \(W^{1,1}_0(U)\).
If \(n\ge 2\) we may use the Rellich–Kondrachov compactness theorem [10, 5.7] for example and [16, Theorem 21.2.9] to conclude that \((u_h)\) converges strongly to u in \(L^1(U)\). Now
and the right-hand side converges to zero as \(h\rightarrow \infty \) as \((f_h)\) is bounded in \(L^\infty (U)\). This shows that \(J(f_h)\rightarrow J(f)\) as \(h\rightarrow \infty \).
In the case \(n=1\) we use the fact that \(W^{1,2}_0(U)\) is compactly embedded in \(C^0(\overline{U})\) (see [13, Theorem 7.22]) and hence in \(L^1(U)\).
(ii) Let \(f\in \mathscr {V}_t\). By Dirichlet’s principle [10, 2.2.5] for example,
The functional E is concave so that J is convex. \(\square \)
Lemma 2.5
Let \(t\in (0,\,V(U))\). A function f in the convex set \(\mathscr {V}_t\subset L^2(U)\) is extremal only if \(f=\chi _A\) \(\mathscr {L}^n\)-a.e. on U for some \(A\subset U\) measurable with \((\psi ,\chi _A)\le t\).
Proof
The proof runs as in [11, Lemma 2]. A measurable function f on U is \(\mathscr {L}^n\)-a.e. equivalent to \(\chi _A\) for some \(A\subset U\) measurable if and only if \(f(1-f)=0\) \(\mathscr {L}^n\)-a.e. on U. Suppose that \(f\in \mathscr {V}_t\) is an extremal element and assume that \(\vert \{f(1-f)\ne 0\}\vert >0\) for a contradiction. Then there exists \(\varepsilon >0\) and a measurable set E in U with positive \(\mathscr {L}^n\)-measure such that \(\varepsilon \le f\le 1-\varepsilon \text { on }E\). Decompose E into two disjoint sets \(E_1,\,E_2\) each with positive \(\mathscr {L}^n\)-measure. Choose \(\alpha =(\alpha _1,\,\alpha _2)\in \mathbb {R}^2\setminus \{0\}\) such that \(\alpha _1(\psi ,\,\chi _{E_1})+\alpha _2(\psi ,\,\chi _{E_2})=0\) and define
for \(\tau \in \mathbb {R}\). Then \(f_\tau \in \mathscr {V}_t\) for \(|\tau |\le \varepsilon /|\alpha _1|\vee |\alpha _2|\). We then derive the contradiction that f is not extremal as \(f=(1/2)\left\{ f_\tau +f_{-\tau }\right\} \) for such \(\tau \). \(\square \)
Proof of Theorem 2.1
Let \((f_h)\) be a maximising sequence for \(\beta (U,t)\). Now \(\mathscr {V}_t\) is weakly sequentially compact in \(L^2(U)\). This follows by appeal to [16, Theorem 10.2.9] due to the fact that \(\mathscr {V}_t\) is bounded, closed and convex in the reflexive Banach space \(L^2(U)\). So we may assume that \((f_h)\) converges weakly in \(L^2(U)\) to some \(f\in \mathscr {V}_t\) as \(h\rightarrow \infty \) after choosing a subsequence if necessary. By Lemma 2.4 (i),
giving item (i) of the Theorem. It is straightforward to see that \((\psi ,\,f)=t\) and hence (ii).
We now argue as in [8, Corollary 6.2]. By [5, Chapitre II §7 Proposition 1.1 (EVT II.58)], J attains its supremum on \(\mathscr {V}_t\) at an extremal point f. We then invoke Lemma 2.5 to conclude that f has the form \(f=\chi _A\) \(\mathscr {L}^n\)-a.e. on U for some measurable set A in U and hence (iii). \(\square \)
3 Some Partial Regularity Results
Proposition 3.1
Suppose that U is a \(C^{1,1}\) domain. Let \(E\subset U\) be a measurable set and \(u=u_E\). Then \(V(\{u=t\psi \})=0\) for each \(t\in (0,1)\).
Proof
By [13, Theorem 9.15], \(u\in W^{2,p}(U)\) for any \(1<p<\infty \). Put \(v:=u-t\psi \), \(N_t:=\{v=0\}\) and assume that \(|N_t|>0\). By [13, Lemma 7.7], we derive that \(D^\alpha v=0\) \(\mathscr {L}^n\)-a.e. and hence V-a.e. on \(N_t\) for any multi-index \(\alpha \) with \(|\alpha |=1\). Observe that \(D^\alpha v\) belongs to \(W^{1,p}(U)\) for \(|\alpha |\le 1\). Applying the last-mentioned lemma once more, we see \(D^\alpha v=0\) V-a.e. on \(N_t\) for any multi-index \(\alpha \) with \(|\alpha |\le 2\). So \(-\Delta v=0\) V-a.e. on \(N_t\). But \(-\Delta v=\chi _E-t\,\chi _U\) V-a.e. on U. This leads to a contradiction. \(\square \)
We require a version of the bathtub principle (see [17, Theorem 1.14]). Let \((X,\mathscr {A},\mu )\) be a finite measure space and \(\rho \) a positive \(\mathscr {A}\)-measurable integrable function on X. Given \(0<v<\mu (X)\), consider the variational problem
where the supremum is taken over measurable sets \(E\subset X\) with \(\mu (E)=v\). We say that measurable sets A, B in X are equivalent \(\mu \)-a.e. and write \(A=B\) if and only if \(\mu (A\Delta B)=0\).
Theorem 3.2
Assume that
Then for each \(v\in (0,\mu (X))\) the problem (3.1) has a unique optimiser up to equivalence \(\mu \)-a.e. given by \(E=\{\rho >s\}\) where
Proof
The distribution function \(\mu _\rho :(0,\infty )\rightarrow (0,V(U));\tau \mapsto \mu (\{\rho >\tau \})\) is non-increasing and right-continuous on \((0,\infty )\); in fact, continuous thanks to (3.2). By right-continuity of \(\mu _\rho \), \(\mu _\rho (s)\le v\); by left-continuity, the reverse inequality holds, so \(\mu (E)=\mu _\rho (s)=v\). For a measurable set A in X with \(\mu (A)=v\),
according to the layer cake representation [17, Theorem 1.13]. It follows that E is an optimiser for (3.1).
Suppose A is a measurable set in X with \(\mu (A)=v\) which is not \(\mu \)-a.e. equivalent to E. Then
so \(\mu (E\setminus A)>0\) as otherwise \(\mu (A\setminus E)=0\) and A is \(\mu \)-a.e. equivalent to E. By countable additivity,
Thus,
where the strict inequality follows from (3.3). \(\square \)
Let U be a \(C^{1,1}\) domain and \(p\in (0,1)\). Let (u, E) be an optimal pair for (1.2) with data (U, p). By [13, Corollary 9.18] we may assume that \(u\in C^0(\overline{U})\).
Proposition 3.3
Suppose that U is a \(C^{1,1}\) domain. Let \(p\in (0,1)\) and suppose that (u, E) is an optimal pair for (1.2) with data (U, p). Then \(V(E\Delta \{u>c\psi \})=V(E\Delta \{u\ge c\psi \})=0\) where \(c\in (0,1)\) is uniquely determined by the condition
Proof
Put \(F:=\{u>c\psi \}\) with c as in (3.4). Assume for a contradiction that \(V(E\Delta F)>0\). We consider a version of Problem (3.1) on U with \(\rho \) replaced by \(w:=u_E/\psi \) and \(\mu \) replaced by V. By Proposition 3.1, \(V(\{w=t\})=0\) for each \(t>0\); thus condition (3.2) holds. By uniqueness of the optimiser in Theorem 3.2 and the Cauchy–Schwarz inequality,
so that \(J(E)<J(F)\), contradicting the assumption that E is an optimal configuration. The identity \(V(E\Delta \{u\ge c\psi \})=0\) follows from Proposition 3.1. \(\square \)
Corollary 3.4
Suppose that U is a \(C^{1,1}\) domain. Let \(p\in (0,1)\) and suppose that (u, E) is an optimal pair for (1.2) with data (U, p). Put \(v:=u-c\psi \) where c is given by (3.4). Then v is a strong solution of the problem
where \(\Omega _\pm (v):=\{\pm v>0\}\) and \(E=\Omega _+(v)\) \(\mathscr {L}^n\)-a.e.
Proof
By [13, Theorem 9.15], \(u\in W^{2,p}(U)\) for any \(1<p<\infty \) and u is a strong solution of \(-\Delta u=\chi _E\). By Proposition 3.3, u is a strong solution of \(-\Delta u=\chi _{\{u>c\psi \}}\). The result follows from the fact that \(-\Delta (c\psi )=c\chi _U\) and Proposition 3.1.\(\square \)
Lemma 3.5
Let \(p\in (0,1)\) and (u, E) be an optimal pair for the data (U, p). Then \((\psi -u,U\setminus E)\) is an optimal pair for the data \((U,1-p)\).
Proof
Let \(A\subset U\) be a measurable set with \(V(A)=pV(U)\). Then
so that \(J(U\setminus A)-V(U)(1-p)^2=J(A)-V(U)p^2\) and the result follows. \(\square \)
Put \(\Gamma _\pm (v)=\partial \Omega _\pm (v)\cap U\).
Lemma 3.6
Suppose that U is a \(C^{1,1}\) domain. Suppose that (u, E) is an optimal pair for the data \((U,\,p)\) and let v be as in Corollary 3.4. Then \(\Gamma _+(v)=\Gamma _-(v)\).
Proof
Suppose that \(x\in \Gamma _+(v)\setminus \Gamma _-(v)\). Then there exists \(r>0\) such that \(B(x,r)\subset U\), \(u\ge c\,\psi \) on B(x, r) and \(u(x)=c\psi (x)\). By Proposition 3.3, \(V(B(x,r)\setminus E)\le V(\{u\ge c\psi \}\setminus E)=0\) and \(B(x,r)\setminus E\) is a Lebesgue null set. Let \(\Phi \) stand for the fundamental solution of Laplace’s equation in \(\mathbb {R}^n\). By the mean-value formula (see [10, 2.5 Problem 3] for example), for any \(0<\tau <r\),
as \(c\in (0,1)\), a contradiction. Here, \(\omega \) is an arbitrary element in the unit sphere \(\mathbb {S}^{n-1}\) in \(\mathbb {R}^n\).
Now suppose that \(x\in \Gamma _-(v)\setminus \Gamma _+(v)\). As before, there exists \(r>0\) such that \(u\le c\,\psi \) on B(x, r) and \(u(x)=c\psi (x)\); alternatively, \(\psi -u\ge (1-c)\,\psi \) on B(x, r) and \((\psi -u)(x)=(1-c)\psi (x)\). By Lemma 3.5, \((\psi -u,U\setminus E)\) is an optimal pair for the data \((U,1-p)\). We then get a contradiction as above. \(\square \)
Put \(\Gamma (v):=\Gamma _+(v)=\Gamma _-(v)\) and \(\Gamma ^*(v):=\Gamma (v)\cap \{|\nabla v|\ne 0\}\). The next theorem follows as in [20, Theorem 4.24].
Theorem 3.7
Suppose that U is a \(C^{1,1}\) domain. Suppose that \((u,\,E)\) is an optimal pair for the data \((U,\,p)\) and that \(x_0\in \Gamma ^*(v)\). Then there exists \(r>0\) such that \(\Gamma (v)\cap B(x,r)\) is a real-analytic hypersurface in B(x, r).
4 Spherical Cap Symmetry
In this section, we replace U by the open unit ball B in \(\mathbb {R}^n\) (\(n\ge 2\)) centred at the origin. We prove the following symmetry result. The notion of spherical cap symmetry is defined below.
Theorem 4.1
Let \(p\in (0,1)\). Suppose that (u, E) is an optimal pair for the data (B, p). Then E possesses spherical cap symmetry \(\mathscr {L}^n\)-a.e.
We first discuss the operation of polarisation for integrable functions on B (see [4] and references therein). For \(\nu \in \mathbb {S}^{n-1}\) the closed half-space \(H=H_\nu \) is defined by
with an associated reflection \(\tau _H:\,\mathbb {R}^n\rightarrow \mathbb {R}^n;\,x\mapsto x - 2\,(x\cdot \nu )\,\nu \). We refer to the collection of closed half-spaces H by \(\mathscr {H}\). The polarisation \(f_H\) of \(f\in L^1_+(B)\) with respect to \(H\in \mathscr {H}\) is defined as follows. Choose an \(\mathscr {L}^n\)-version \(\widetilde{f}\) of f. Set
\(\widetilde{f}_H\) is \(\mathscr {L}^n\)-measurable and its \(\mathscr {L}^n\)-equivalence class \(f_H:=[\widetilde{f}_H]\) is the polarisation of f. The definition is well-defined due to the fact that if \(\widetilde{f}=\widetilde{g}\) \(\mathscr {L}^n\)-a.e. on B then \(\widetilde{f}=\widetilde{g}\) \(\mathcal {H}^{n-1}\)-a.e. on \(\mathbb {S}^{n-1}_\tau \) for \(\mathscr {L}^1\)-a.e. \(0<\tau <1\), and vice-versa.
The Green kernel G(x, y) for B is given by
where \(\Phi \) is the fundamental solution of Laplace’s equation in \(\mathbb {R}^n\) as before, \(\mathtt {d}\) stands for the diagonal in \(B\times B\) and the decoration \(*\) refers to inversion in the unit sphere. We note the inequality
which follows from the strong maximum principle.
Theorem 4.2
Let \(f\in L^1_+(B)\) and \(H\in \mathscr {H}\). Then \(J(f)\le J(f_H)\) with equality if and only if either \(f=f_H\) or \(f\circ \tau _H=f_H\) \(\mathscr {L}^n\)-a.e. on B.
Proof
Let \(\widetilde{f}\) be an \(\mathscr {L}^n\)-version of f. Define
and similarly \(S^+\) but with the strict inequality replaced by the sign \(>\). Put \(A^-:=\tau _H A^+\) and \(A:=A^+\cup A^-\). In this notation,
As a consequence,
and a similar identity holds for J(f) but without composition with reflection. We may then write
It is clear from this representation with the help of (4.1) that \(J(f)\le J(f_H)\).
In the case of equality, it holds that either \(|A^+|=0\) or \(|S^+|=0\). In the former case, \(f=f_H\) while in the latter, \(f\circ \tau _H = f_H\) \(\mathscr {L}^n\)-a.e. on B. \(\square \)
Let \(\omega \in \mathbb {S}^{n-1}\). Given \(0<\tau <1\) and \(0<\alpha \le \pi \) the spherical cap \(C_\omega (\tau ,\alpha )\) is the set
and has volume
For a Borel set E in B put
The function L is Borel measurable The spherical cap symmetrisation of E is the set
where \(\alpha \in (0,\pi ]\) is determined by \(s(\tau ,\,\alpha )=L(\tau )\). Observe that \(C_\omega E\) is a Borel set in B (use Fubini’s Theorem [1, 1.74] for example) and \(|C_\omega E|=|E|\). We say that the Borel set \(E\subset B\) possesses spherical cap symmetry \(\mathscr {L}^n\)-a.e. if \(C_\omega E=E\) up to \(\mathscr {L}^n\)-a.e. equivalence for some \(\omega \in \mathbb {S}^{n-1}\).
Let \(f\in L^1_+(B)\) and choose an \(\mathscr {L}^n\)-version \(\widetilde{f}\) of f. Put \(m_{\widetilde{f}}(\tau ,t):=\mathcal {H}^{n-1}(\{\widetilde{f}>t\}\cap \mathbb {S}^{n-1}_\tau )\) for \(t\in \mathbb {R}\) and \(0\le \tau <1\). The function \(m_{\widetilde{f}}(\tau ,\cdot )\) is non-increasing and right continuous. Define its right continuous inverse by
For \(x\in B\) put \(\tau =|x|\) and choose \(\alpha \in (0,\pi ]\) such that \(x\cdot \omega =\tau \cos \alpha \) then define
Note that \(m_{\widetilde{f}}(\tau ,t)>s\) if and only if \(\widetilde{f}^\sharp (\tau ,s)>t\). It follows that
In particular, \(C_\omega \widetilde{f}\) is Borel measurable and its \(\mathscr {L}^n\)-equivalence class \(C_\omega f:=[C_\omega \widetilde{f}]\) is the spherical cap symmetrisation of f.
Before proving Theorem 4.1, we prepare a number of lemmas. We first discuss a useful two-point inequality. We introduce the notation
Equip Q with the \(\ell ^1\)-norm \(\Vert x\Vert _1:=|x_1|+|x_2|\) and define a mapping \(\varphi :Q\rightarrow Q\) via \((x_1,\,x_2)\mapsto (x_1\vee x_2,\,x_1\wedge x_2)\); \(\varphi \) folds S onto R. A geometric argument establishes the following lemma.
Lemma 4.3
For any \(x,\,y\in Q\), \(\Vert \varphi x - \varphi y\Vert _1\le \Vert x-y\Vert _1\) with strict inequality if and only if \(x\in R\) and \(y\in \overline{S}\) or \(x\in \overline{R}\) and \(y\in S\) or the same with the rôles of x and y interchanged.
For \(\omega \in \mathbb {S}^{n-1}\) introduce the collection of closed half-spaces \( \mathscr {H}_\omega :=\Big \{H_\nu :\,\nu \in \mathbb {S}^{n-1}\text { and }\nu \cdot \omega \ge 0\Big \}\).
Lemma 4.4
Fix \(\omega \in \mathbb {S}^{n-1}\). For any \(H\in \mathscr {H}_\omega \) we have
-
(i)
for any \(f,g\in L^1_+(B)\), \( \Vert f_H - g_H\Vert _{L^1(B)}\le \Vert f - g\Vert _{L^1(B)}; \)
-
(ii)
for any \(f\in L^1_+(B)\), \((C_\omega f)_H=C_\omega f\) \(\mathscr {L}^n\)-a.e. on B;
-
(iii)
for any \(f\in L^1_+(B)\),
$$\begin{aligned} \Vert f_H - C_\omega f\Vert _{L^1(B)}\le \Vert f - C_\omega f\Vert _{L^1(B)} \end{aligned}$$(4.4)with strict inequality if \(|\left\{ f\circ \tau _H > f\right\} \cap H|>0\).
Proof
(i) By Lemma 4.3,
(ii) Let \(f\in L^1_+(B)\) and \(\widetilde{f}\) a \(\mathscr {L}^n\)-representative of f. For \(x\in B\cap H\), \(x\cdot \omega \ge (\tau _H x)\cdot \omega \) so \((C_\omega \widetilde{f})_H=C_\omega \widetilde{f}\) on B. Therefore,
(iii) The inequality follows by (i) and (ii). On \(B\cap H\) the pair \((C_\omega \widetilde{f},C_\omega \widetilde{f}\circ \tau _H)\) belongs to \(\overline{R}\). By Lemma 4.3 if \((\widetilde{f},\widetilde{f}\circ \tau _H)\in S\) on a set of positive measure in \(B\cap H\) then strict inequality holds in (4.4). This observation leads to the criterion in the lemma. \(\square \)
Lemma 4.5
Let \(f\in L^1(\mathbb {S}^{n-1},\mathcal {H}^{n-1})\). Fix \(\nu \in \mathbb {S}^{n-1}\) and let \((\nu _h)\) be a sequence in \(\mathbb {S}^{n-1}\) that converges to \(\nu \) in \(\mathbb {S}^{n-1}\). Then
Proof
Note that \(|\tau _h x-\tau x|\le 4|\nu _h-\nu |\) for each \(x\in \mathbb {S}^{n-1}\) and h. Now use the density of \(C(\mathbb {S}^{n-1})\) in \(L^1(\mathbb {S}^{n-1},\mathcal {H}^{n-1})\) and the fact that each \(\tau ,\tau _h\) is an isometry on \(L^1(\mathbb {S}^{n-1},\mathcal {H}^{n-1})\).\(\square \)
The next lemma is a spherical cap symmetrisation counterpart to [4, Lemma 6.3] and extends [23, Lemma 3.9].
Lemma 4.6
Let \(f\in L^1_+(B)\) and \(\omega \in \mathbb {S}^{n-1}\) and assume that \(f\ne C_\omega f\). Then there exists \(H\in \mathscr {H}_\omega \) such that
Proof
For non-negative Borel measurable functions f, g on B, \(f=g\) if and only if \(|\{f>t\}\Delta \{g>t\}|=0\) for any \(t>0\). As \(f\ne C_\omega f\) there exists \(t>0\) such that
By (4.3) \(|\{f>t\}|=|\{C_\omega f>t\}|\) and it follows that \(|\{f\le t< C_\omega f\}|=|\{C_\omega f\le t< f\}|\). Put \(A:=\left\{ f\le t<C_\omega f\right\} \) and \(A^\prime :=\left\{ C_\omega f\le t<f\right\} \). For later use we note that
for \(\mathscr {L}^1\)-a.e. \(\tau \in (0,1)\).
We claim there exists \(H\in \mathscr {H}_\omega \) such that \(|A\cap \tau _H A^\prime |>0\). Taking this as read, on \(A\cap \tau _H A^\prime \) we have that \(C_\omega f>t\ge C_\omega f\circ \tau _H\) so that \(A\cap \tau _H A^\prime \subset H\). Also, \(f\le t<f\circ \tau _H\) there. In short, \(A\cap \tau _H A^\prime \subset \left\{ f\circ \tau _H>f\right\} \cap H\). So \(|\left\{ f\circ \tau _H>f\right\} \cap H|>0\) and strict inequality holds by Lemma 4.4 (iii).
To prove the claim, assume for a contradiction that \(|A\cap \tau _H A^\prime |=0\) for all \(H\in \mathscr {H}_\omega \). Let F be a countable dense subset in \(\mathbb {S}^{n-1}\cap H_\omega \). Then
Therefore for all \(r\in (0,1)\) it holds that
except on a \(\mathscr {L}^1\)-null set \(N\subset (0,1)\). We write \(A_r:=A\cap \mathbb {S}^{n-1}_r\) for the r-section of A and likewise for \(A^\prime \). Let \(\nu \in \mathbb {S}^{n-1}\cap H_\omega \) with corresponding reflection \(\tau =\tau _{H_\nu }\). Select a sequence \((\nu _h)\) in F which converges to \(\nu \) in \(\mathbb {S}^{n-1}\) and write \(\tau _h\) for the reflection associated to the closed half-space \(H_{\nu _h}\). For \(r\in (0,\,1)\setminus N\),
and this latter converges to zero as \(h\rightarrow \infty \) by Lemma 4.5. We derive that
for all \(r\in (0,\,1)\setminus N\).
To conclude the argument, choose \(r\in (0,1)\setminus N\) such that \(\mathcal {H}^{n-1}(A_r)=\mathcal {H}^{n-1}(A^\prime _r)>0\). Select a density point x for \(A_r\) lying in \(A_r\) using [1, Corollary 2.23] for example; that is,
This means that \(A_r\) has density 1 at x in the sense that
Choose y in \(A^\prime _r\) similarly so that \(A^\prime _r\) has density 1 at y. Then \(C_\omega f(x)>t\ge C_\omega f(y)\). So there exists \(\nu \in \mathbb {S}^{n-1}\cap H_\omega \) such that with \(\tau =\tau _{H_\nu }\) we have that \(\tau y = x\). But then
so that, in fact, \(\mathcal {H}^{n-1}(A_r\cap \tau B_r)>0\), contradicting (4.5). \(\square \)
Proof of Theorem 4.1
Let E be an optimal configuration for the data (U, p). Assume for a contradiction that \(E\ne C_\omega E\) \(\mathscr {L}^n\)-a.e. for any \(\omega \in \mathbb {S}^{n-1}\). Then there exists \(\omega \in \mathbb {S}^{n-1}\) such that
By Lemma 4.6 there exists \(H\in \mathscr {H}_\omega \) such that \(\Vert (\chi _E)_H-C_\omega \chi _E\Vert _{L^1(B)}<\Vert \chi _E-C_\omega \chi _E\Vert _{L^1(B)}\). It is plain from this that \(\chi _E\ne (\chi _E)_H\); but also \(\chi _E\circ \tau _H\ne (\chi _E)_H\), for otherwise,
contradicting optimality of \(\omega \). It follows by Theorem 4.2 that \(J(E)<J(E_H)\), contradicting the fact that E is an optimal configuration for the data (U, p). The result now follows. \(\square \)
5 Preliminaries on Weighted Dirichlet Forms
Let \(n=1\) and \(U=(a,b)\) be an open bounded interval in \(\mathbb {R}\). We are given a density function w with the property
-
(A)
w is a positive function in \(C_0(U)\).
The weighted volume of an \(\mathscr {L}^1\)-measurable set E in U is given by \(m(E):=\int _E w\,dx\). We introduce the further assumption
-
(B)
\(w\in C^1(U)\) and \(w^\prime /w\in L^2(U,m)\).
Consider the coercive bilinear form
in \(L^2(U,m)\).
Lemma 5.1
Assume (A)–(B). Then
-
(i)
\((\mathscr {D},\mathscr {E})\) is closable in \(L^2(U,m)\) with closure denoted \((D(\mathscr {E}),\mathscr {E})\);
-
(ii)
\((D(\mathscr {E}),\mathscr {E})\) is a symmetric Dirichlet form in \(L^2(U,m)\).
Proof
We refer to [19, Definitions I.2.3 and I.4.5] (for example). Note that \((\mathscr {D},\mathscr {E})\) satisfies the weak sector condition [19] (2.3) by the Cauchy–Schwarz inequality. Suppose \((u_h)\) is a sequence in \(\mathscr {D}\) such that \(u_h\rightarrow 0\) in \(L^2(U,m)\). For \(v\in \mathscr {D}\) an integration-by-parts gives
as \(h\rightarrow \infty \) where \(\nu =\pm 1\) is the one-dimensional unit exterior normal on \(\partial U\). We have made use of the assumptions (A) and (B). The statement (i) follows by [19, Lemma I.3.4]. Then \((D(\mathscr {E}),\mathscr {E})\) is a symmetric closed form by definition (cf. [19, Definition I.2.3]). By [19, Proposition I.4.10 and II.2 (c)], \((D(\mathscr {E}),\mathscr {E})\) is a symmetric Dirichlet form. \(\square \)
Given a real-valued function u on \(\mathbb {R}_+\) (or \(\mathbb {R})\) define the function \(\theta _t u\) on \(\mathbb {R}_+\) for each \(t>0\) by \((\theta _t u)(x):=u(x+t)\) for \(x\in \mathbb {R}_+\) (or \(\mathbb {R})\).
Lemma 5.2
Let \(\lambda \) be a positive \(\mathscr {L}^1\)-integrable function on \(\mathbb {R}_+\) such that
Then
-
(i)
\(\theta _t\in B(L^2(\mathbb {R}_+,\lambda \mathscr {L}^1))\) for each \(t>0\);
-
(ii)
\(\Vert u-\theta _t u\Vert _{L^2(\mathbb {R}_+,\lambda \mathscr {L}^1)}\rightarrow 0\) as \(t\downarrow 0\) for each \(u\in L^2(\mathbb {R}_+,\lambda \mathscr {L}^1)\).
Proof
(i) For any \(u\in L^2(\mathbb {R}_+,\lambda \mathscr {L}^1)\),
(ii) The statement holds for \(u\in C([0,\infty ))\cap L^2(\mathbb {R}_+,\lambda \mathscr {L}^1)\) by the dominated convergence theorem and this latter set is dense in \(L^2(\mathbb {R}_+,\lambda \mathscr {L}^1)\). These observations as well as (i) lead to the result using a \(3\varepsilon \)-argument. \(\square \)
Our next assumption is stronger than required but easy to state:
-
(C)
w is unimodal on U.
Lemma 5.3
Assume (A)–(C). Then
Proof
Let \(u\in D(\mathscr {E})\). There exists a Cauchy sequence \((u_h)\) in \((\mathscr {D},\mathscr {E})\) which converges to u in \(L^2(U,m)\). Then \((u_h^\prime )\) is a Cauchy sequence in \(L^2(U,m)\) with limit \(v\in L^2(U,m)\) (say). For \(\phi \in C^\infty _c(U)\),
so u is weakly differentiable on U with weak derivative \(u^\prime =v\in L^2(U,m)\).
Now let \(u\in L^2(U,m)\) be weakly differentiable on U such that \(u^\prime \in L^2(U,m)\). Multiplying by a partition of unity we may assume that \(u=0\) near b. Denote by \(\overline{u}\) the extension of u to \(\mathbb {R}\) by zero. For \(t>0\) put \(v_t:=(\theta _t\overline{u})\vert _U\). Note that \(v_t\) is weakly differentiable and \(v_t^\prime =\theta _t(\overline{u^\prime })\vert _U\). For \(t>0\), \(v_t, v_t^\prime \in L^2(U,m)\). Let \((\rho _\varepsilon )_{\varepsilon >0}\) be a family of mollifiers on \(\mathbb {R}\) (cf. [1, 2.1]). For \(t>0\) and \(\varepsilon >0\) small, \((\rho _\varepsilon \star (\theta _t\overline{u}))^\prime =\rho _\varepsilon \star (\theta _t\overline{u^\prime })\) on U. The operation \(\star \) stands for convolution. For \(t>0\) and \(\varepsilon >0\) small put \(w_{t,\varepsilon }:=\rho _\varepsilon \star (\theta _t\overline{u})\vert _U\in C^\infty (\overline{U})\). Now
By Lemma 5.2 and (A)–(C) the expressions \(\Vert u-v_t\Vert _{L^2(U,m)}\) and \(\Vert u^\prime -v^\prime _t\Vert _{L^2(U,m)}\) are small for \(t>0\) small. We also use the fact that the mollified functions are regular approximations in \(L^2\) (cf. [1, 2.1]). This shows that \(u\in D(\mathscr {E})\). \(\square \)
Suppose that \(\hat{U}=(c,d)\) is an open bounded interval in \(\mathbb {R}\) and \(\Phi :\hat{U}\rightarrow U\) is a \(C^1\) bijection such that \(\Phi ^\prime =:\varphi >0\) on \(\hat{U}\). Let \(\hat{m}:=\Phi _\sharp m\) be the pull-back of m under \(\Phi \); thus \(\hat{m}=\hat{w}\mathscr {L}^1\) on \(\hat{U}\) where \(\hat{w}:=\varphi (w\circ \Phi )\). Define a coercive bilinear form

in \(L^2(\hat{U},\hat{m})\) with domain
Lemma 5.4
Assume (A)–(C). Then
-
(i)
\((D(\hat{\mathscr {E}}),\hat{\mathscr {E}})\) is a symmetric Dirichlet form in \(L^2(\hat{U},\hat{m})\);
-
(ii)
the mapping \(D(\hat{\mathscr {E}})\rightarrow D(\mathscr {E});u\mapsto \overline{u}:=u\circ \Phi ^{-1}\) is a Hilbert space isomorphism.
Proof
(i) We show that \((D(\hat{\mathscr {E}}),\hat{\mathscr {E}})\) is closed in \(L^2(\hat{U},\hat{m})\). Let \((u_h)\) be an \(\hat{\mathscr {E}}^{1/2}\)-Cauchy sequence in \(D(\hat{\mathscr {E}})\). Then \((u_h)\) resp. \((\varphi ^{-1}u_h^\prime )\) are Cauchy sequences in \(L^2(\hat{U},\hat{m})\) with limits \(u\in L^2(\hat{U},\hat{m})\) resp. \(v\in L^2(\hat{U},\hat{m})\). For \(\phi \in C^\infty _c(\hat{U})\),
so u is weakly differentiable and \(\varphi ^{-1}u^\prime =v\); that is, \(u\in D(\hat{\mathscr {E}})\). It then follows that \((u_h)\) converges to u in \(\hat{\mathscr {E}}^{1/2}\)-norm. So \((D(\hat{\mathscr {E}}),\hat{\mathscr {E}})\) is a symmetric closed form in \(L^2(\hat{U},\hat{m})\).
Let \(u\in D(\hat{\mathscr {E}})\). Given \(\varepsilon >0\) let \(\varphi _\varepsilon \) be as in [19, Example II.2.7]. Note that \(u\in W^{1,2}_{\mathrm {loc}}(\hat{U})\). Then \(\varphi _\varepsilon (u)\) is weakly differentiable on \(\hat{U}\) and \(\varphi _\varepsilon (u)^\prime =\varphi _\varepsilon ^\prime (u)u^\prime \) (see for example [10, 5.10, Exercise 16]) so \(\varphi _\varepsilon (u)\in D(\hat{\mathscr {E}})\). We then derive that
By [19, Proposition I.4.7], \((D(\hat{\mathscr {E}}),\hat{\mathscr {E}})\) is a symmetric Dirichlet form in \(L^2(\hat{U},\hat{m})\).
(ii) Let \(u\in D(\hat{\mathscr {E}})\). Note that \((u^\prime /\varphi )\circ \Phi ^{-1}\in L^2(U,m)\) (use [1, (2.47)]) and \(\overline{u}\) is weakly differentiable on U with \(\overline{u}^\prime =(u^\prime /\varphi )\circ \Phi ^{-1}\in L^2(U,m)\). Thus the mapping is well-defined. For \(u,v\in D(\hat{\mathscr {E}})\), \(\hat{\mathscr {E}}(u,v)=\mathscr {E}(\overline{u},\overline{v})\) again using [1, (2.47)]. In particular, the mapping \(u\mapsto \overline{u}\) is injective. Now let \(u\in D(\mathscr {E})\) and put \(\hat{u}:=u\circ \Phi \). Then \(\hat{u}\in L^2(\hat{U},\hat{m})\), \(\hat{u}\) is weakly differentiable on \(\hat{U}\) with weak derivative \(\hat{u}^\prime =\varphi (u^\prime \circ \Phi )\) and \(\varphi ^{-1}\hat{u}^\prime \in L^2(\hat{U},\hat{m})\); in other words, \(\hat{u}\in D(\hat{\mathscr {E}})\). This shows that the mapping in (ii) is surjective.\(\square \)
Now take \(B=(-1,1)\). We are given density functions f, g with the properties
-
(A.1)
f is a positive function in C(B);
-
(A.2)
g is a positive unimodal function in \(C_0(B)\).
The weighted volume of an \(\mathscr {L}^1\)-measurable set E in B is given by \(V(E):=\int _E f\,dx\). Put \(\rho :=f/g\). We introduce the further assumption
-
(A.3)
\(\rho \in L^1(B,\mathscr {L}^1)\), \(g\in C^1(B)\) and \(g^\prime /f\in L^2(B,V)\).
Define
and let \(\check{B}\) denote the image of B under R; \(\check{B}\) is an open bounded interval in \(\mathbb {R}\). Then \(R:B\rightarrow \check{B}\) is a \(C^1\) bijection. Define \(\check{g}:=g\circ R^{-1}\) on \(\check{B}\). Define the measure \(\check{V}:=\check{g}\mathscr {L}^1\) on \(\check{B}\).
We introduce coercive bilinear forms
in \(L^2(\check{B},\check{V})\) with domain
and

in \(L^2(B,V)\) with domain
Note that with \(\check{B}\) in place of U, \(w:=\check{g}\) satisfies properties (A)–(C) above in light of the assumptions (A.1)–(A.3). We derive
Lemma 5.5
Assume (A.1)–(A.3). Then
-
(i)
\((D(\check{\mathscr {E}}),\check{\mathscr {E}})\) is a symmetric Dirichlet form in \(L^2(\check{B},\check{V})\);
-
(ii)
\(C^\infty (\overline{\check{B}})\) is dense in \(D(\check{\mathscr {E}})\) with respect to the \(\check{\mathscr {E}}^{1/2}\)-norm;
-
(iii)
\((D(\hat{\mathscr {E}}),\hat{\mathscr {E}})\) is a symmetric Dirichlet form in \(L^2(B,V)\);
-
(iv)
the mapping \(D(\hat{\mathscr {E}})\rightarrow D(\check{\mathscr {E}});u\mapsto u\circ R^{-1}\) is a Hilbert space isomorphism.
6 An (f, g)-Isoperimetric Inequality
Recall that an \(\mathscr {L}^1\)-measurable set \(E\subset B\) is said to be a Caccioppoli set if for each relatively compact open set \(\Omega \) in B,
There then exists a unique real Radon measure \(D\chi _E\) on B such that
for all \(\phi \in C^\infty _c(B,\mathbb {R})\) [1, Corollary 1.55]. Denote by \(|D\chi _E|\) the total variation measure of \(D\chi _E\).
Theorem 6.1
Suppose that E is a Caccioppoli set in B with \(|E|>0\). Then there exist \(N\in \mathbb {N}\cup \{\infty \}\) and closed intervals \(E_h=[a_{2h-1},a_{2h}]\subset \mathbb {R}\) \((h=1,\ldots ,N)\) with non-empty interior and separated by open neighbourhoods in \(\mathbb {R}\) such that E is \(\mathscr {L}^1\)-a.e. equivalent to the union of the \(E_h\).
The statement that the collection of intervals \((E_h)\) is separated by open intervals means that \(\inf _{k\ne h}d(E_h,E_k)>0\) for each h. Here, d denotes the standard metric on \(\mathbb {R}\).
Proof
The proof is along the lines of [1, Proposition 3.52]. Put \(u:=\chi _E\in \mathrm {BV}_{\mathrm {loc}}(B)\). Then \(\mu :=Du\) is a real Radon measure on B [1, 1.40]. Define
w is left-continuous on B by the Hahn decomposition and inner/outer regularity [1, 1.43]. By Fubini’s theorem, \(w\in \mathrm {BV}_{\mathrm {loc}}(B)\) and \(Dw=\mu \). By [1, Proposition 3.2], \(u=c+w\) \(\mathscr {L}^1\)-a.e. on B for some \(c\in \mathbb {R}\). Let A be the set of atoms of \(\mu \) in B. Note that w is continuous on \(B\setminus A\) and \(w(t+)-w(t)=\mu (\{t\})\) at each \(t\in A\). As \(c+w\in \{0,1\}\) \(\mathscr {L}^1\)-a.e. on B, \(\mu (\{t\})\in \{-1,1\}\) for each \(t\in A\). Let \(\Omega \) be a relatively compact open set in B. Then \(\mathrm {Card}(A\cap \Omega )=|\mu |(A\cap \Omega )\le |\mu |(\Omega )<\infty \). Thus the set of atoms A accumulates at \(\partial B\) (if at all). By the observations above, the function \(c+w\) is constant on each connected component of \(B\setminus A\) with values in the set \(\{0,1\}\). Let the sets \(E_h\) be the closure of the open intervals in \(B\setminus A\) where \(c+w\) takes the value 1.\(\square \)
Let g be a positive lower semicontinuous function on B. Let E be a Caccioppoli set in B. The g-perimeter of E relative to B is defined by
Lemma 6.2
Let g be a positive lower semicontinuous function on B and E a Caccioppoli set in B. Then
where A stands for the set of atoms of \(D\chi _E\) in B.
Proof
A direct computation gives \(D\chi _E=\sum _{a\in A}D\chi _E(\{a\})\delta _a\) and \(|D\chi _E|=\sum _{a\in A}\delta _a\) which gives the result. We use \(\delta _a\) to stand for the Dirac measure at a.\(\square \)
Let f, g be densities on B satisfying conditions (A.1)–(A.3). The weighted volume of an \(\mathscr {L}^1\)-measurable set E in B is the measure given by \(V(E):=\int _E f\,dx\). Define \(F:[-1,1]\rightarrow [0,V(B)]\) by \(F(x):=V((-1,x))\) and
We impose the additional assumptions
-
(A.4)
\(J(p)=J(V(B)-p)\) for \(0<p<V(B)\);
-
(A.5)
for all \(p,q>0\) with \(p+q<V(B)\), \(J(p+q)<J(p)+J(q)\).
For an \(\mathscr {L}^1\)-measurable set E in B the \(\bigstar \)-rearrangement of E is defined by \(E^\bigstar :=(-1,F^{-1}(V(E)))\). We then have that the following (f, g)-isoperimetric inequality is valid.
Theorem 6.3
Assume (A.1)–(A.5). Suppose that E is a Caccioppoli set in B. Then \(P_g(E,B)\ge P_g(E^\bigstar ,B)\).
Proof
For \(0<p<q<V(B)\),
by (A.4)–(A.5). The above inequality also holds for \(0\le p<q\le V(B)\) with \(>\) replaced by \(\ge \) by continuity; equality holds if and only if one or both of p, q are extremal.
We may suppose that \(V(E)=p\) for some \(p\in (0,V(B))\). Assume that E has the form \(E=\bigcup _{h=1}^N[a_{2h-1},a_{2h}]\) with \(-1\le a_1<a_2<\cdots <a_{2N-1}<a_{2N}\le 1\) for some \(N\in \mathbb {N}\). Put \(p_j:=F(a_j)\) so that \(0\le p_1<\cdots < p_{2N}\le V(B)\) and \(\sum _{h=1}^N(p_{2h}-p_{2h-1})=p\). By Lemma 6.2, (6.2) and (A.5),
The result for arbitrary E as in the statement follows by Theorem 6.1, the monotone convergence theorem and continuity of J. \(\square \)
We now investigate the equality case in the isoperimetric inequality.
Theorem 6.4
Assume (A.1)–(A.5). Suppose that E is a Caccioppoli set in B. Assume that \(P_g(E,B) = P_g(E^\bigstar ,B)\). Then either \(E=E^\bigstar \) or \(B\setminus E=(B\setminus E)^\bigstar \) V-a.e.
Proof
We may assume that E is the union of closed intervals \(E_h\subset \mathbb {R}\) \((h=1,\ldots ,N, N\in \mathbb {N}\cup \{\infty \})\) with non-empty interior and separated by open neighbourhoods in \(\mathbb {R}\) as in Theorem 6.1. In virtue of (6.1) we may take \(N>1\). We can then find \(x\in B\setminus E\) such that \(V(E\cap (x,1))>0\) and \(V(E\cap (-1,x))>0\). Put \(E_-:=E\cap (-1,x)\), \(E_+:=E\cap (x,1)\), \(F_-:=E_-^\bigstar \) and \(F_+:=B\setminus (B\setminus E_+)^\bigstar \). Note that \(V(E_-)=V(F_-)=p_-\) and \(V(E_+)=V(F_+)=p_+\) for some \(p_\pm \in (0,V(B))\). We have
by Theorem 6.3. On the other hand, \(P_g(E,B)=P_g(E^\bigstar ,B)=J(p_-+p_+)<J(p_-)+J(p_+)\) by (A.5), a contradiction.\(\square \)
Proposition 6.5
Assume (A.1)–(A.3). If \(g^\prime /f\) is strictly decreasing on B then (A.5) holds.
Proof
Note that J is differentiable on (0, V(B)). Moreover, \((F^{-1})^\prime (p)=1/(f\circ F^{-1})(p)\) and
for \(p\in (0,V(B))\); this shows that J is strictly concave on (0, V(B)) as \((0,V(B))\mapsto (-1,1):\,p\mapsto (F^{-1})(p)\) is increasing. For \(0<p<q<V(B)\) we have that
by concavity and the fact that \(J(0)\ge 0\). Supposing additionally that \(p+q<V(B)\) we have
by considering the gradient of chords. Rearranging and using (6.3) gives (A.5).\(\square \)
Let u be a real-valued \(\mathscr {L}^1\)-measurable function on B. Put \(\mu _u(t):=V(\{|u|>t\})\) for \(t\ge 0\). The function \(\mu _u:[0,\infty )\rightarrow [0,V(B)]\) is non-increasing, right-continuous and \(\mu _u(t)\rightarrow 0\) as \(t\rightarrow \infty \). Define its right-continuous inverse \(u^\sharp :[0,V(B)]\rightarrow [0,\infty ]\) by
with the understanding that \(\inf \emptyset =+\infty \). Define \(u^\bigstar :=u^\sharp \circ F\) on B. Note that \(\mu _u(t)>s\) if and only if \(u^\sharp (s)>t\) (see Lemma 10.1). It follows that
in fact, \(V(\{u^\bigstar >t\})=V(\{F<\mu _u(t)\})=V((-1,F^{-1}(\mu _u(t))))=\mu _u(t)\).
The following result is a Hardy–Littlewood type inequality and can be proved as in [14, 13.10] (see also [9, Theorem 3]).
Theorem 6.6
Assume (A.1)–(A.5). Let u, v be real-valued \(\mathscr {L}^1\)-measurable functions on B. Then
The next non-expansivity result can be found in [9, Corollary 1].
Theorem 6.7
Assume (A.1)–(A.5). Let u, v be real-valued \(\mathscr {L}^1\)-measurable functions on B. Then
Define a metric \(\hat{d}\) on B as follows. The length of a piecewise \(C^1\) parametrised curve \(\gamma :[\alpha ,\beta ]\rightarrow B\) in \((B,\hat{d})\) is
For \(x,y\in B\), \(\hat{d}(x,y)\) stands for the infimum of lengths of piecewise \(C^1\) parametrised curves in B connecting x to y; \(\hat{d}(\cdot ,\cdot )\) is a metric on B.
Lemma 6.8
For \(x,y\in B\), \(\hat{d}(x,y)=d(R(x),R(y))\).
Proof
Let \(\gamma :[\alpha ,\beta ]\rightarrow B\) be a piecewise \(C^1\) parametrised curve in B connecting x to y. Then \(\hat{L}[\gamma ]=L[R\circ \gamma ]\) in an obvious notation. So \(\hat{d}(x,y)\le d(R(x),R(y))\). A similar argument gives the reverse inequality.\(\square \)
Note that for each \(\mathscr {L}^1\)-measurable set E in B, \(\check{V}(R(E))=V(E)\).
Lemma 6.9
The mapping \(R:B\rightarrow \check{B}\) sets up a one-to-one correspondence between Caccioppoli sets in B resp. \(\check{B}\). Moreover, let E be a Caccioppoli set in B. Then
-
(i)
\(|D\chi _{R(E)}|=R_\sharp |D\chi _{E}|\);
-
(ii)
\(P_{\check{g}}(R(E),\check{B})=P_g(E,B)\).
Proof
Let \(\Omega \subset B\) be a relatively compact open set. Then
from which the first assertion follows. Item (i) follows from the definition of the push-forward [1, Definition 1.7] and the coincidence criterion [1, Proposition 1.8], while (ii) follows from (6.1), (i) and the change of variables formula for integrals. \(\square \)
The function \(\check{F}:\mathbb {R}\rightarrow [0,V(B)]\) defined by \(\check{F}(x):=\check{V}(\check{B}\cap (-\infty ,x))\) is the cumulative distribution function of \(\check{g}\). Let u be a real-valued \(\mathscr {L}^1\)-measurable function on \(\check{B}\). Put \(\check{\mu }_{u}(t):=\check{V}(\{|u|>t\})\) for \(t\ge 0\) and denote by \(\check{u}^{\sharp }:[0,\check{V}(\check{B})]\rightarrow [0,\infty ]\) its right-continuous inverse (as in the Appendix). Define \(u^\star :=\check{u}^{\sharp }\circ \check{F}\) on \(\check{B}\).
Proposition 6.10
Let u be a real-valued \(\mathscr {L}^1\)-measurable function on B and put \(v:=u\circ R^{-1}\). Then \(u^\bigstar =v^\star \circ R\). In particular, for any \(\mathscr {L}^1\)-measurable set \(E\subset B\), \(R(E)^\star =R(E^\bigstar )\).
Proof
We have that \(\mu _u(t)=\check{\mu }_{v}(t)\) for each \(t\ge 0\); hence \(u^\sharp =\check{v}^{\sharp }\) on [0, V(B)]. Now , \(\check{F}\circ R=F\) on \([-1,1]\). This leads to the first claim. The second then follows straightforwardly.\(\square \)
Corollary 6.11
Assume (A.1)–(A.5). Suppose that E is a Caccioppoli set in \(\check{B}\). Then \(P_{\check{g}}(E,\check{B})\ge P_{\check{g}}(E^\star ,\check{B})\).
Proof
Let E be a Caccioppoli set in B. By Lemma 6.9, Theorem 6.3 and Proposition 6.10,
\(\square \)
Corollary 6.12
Assume (A.1)–(A.5). Suppose that E is a Caccioppoli set in \(\check{B}\). Assume that \(P_{\check{g}}(E,\check{B}) = P_{\check{g}}(E^\star ,\check{B})\). Then either \(E=E^\star \) or \(\check{B}\setminus E=(\check{B}\setminus E)^\star \) \(\check{V}\)-a.e.
Proof
This follows from Lemma 6.9 and Theorem 6.4.\(\square \)
Finally, we state a counterpart of Theorem 6.7.
Theorem 6.13
Assume (A.1)–(A.5). Let u, v be real-valued \(\mathscr {L}^1\)-measurable functions on \(\check{B}\). Then
7 A Pólya–Szegö Inequality
We first show that the rearrangement \(\cdot ^\star \) is smoothing in the sense of [21] (see also [4]). Given \(r>0\) write \(E_r\) for the r-neighbourhood of an \(\mathscr {L}^1\)-measurable set E in \((\check{B},d)\); by convention, \(\emptyset _r=\emptyset \). The Minkowski content of E is the quantity
Lemma 7.1
Let E be a finite union of open intervals in \((\check{B},d)\). Then
-
(i)
E is a Caccioppoli set in \(\check{B}\);
-
(ii)
\(\check{V}^+(E)=P_{\check{g}}(E,\check{B})\).
Proof
(i) The set E is a finite union of disjoint open intervals, \(\overline{E}\) is a finite union of closed intervals in \(\mathbb {R}\) with non-empty interior and separated by open sets in the sense of Theorem 6.1 and \(\overline{E}=E\cup I\) for a finite set \(I\subset \mathbb {R}\). So E is \(\mathscr {L}^1\)-a.e. equivalent to \(F:=\overline{E}\cap \check{B}\); in particular, E is a Caccioppoli set in \(\check{B}\) by Theorem 6.1.
(ii) Suppose first that \(F=[a_1,a_2]\subset \check{B}\). Then \(E_r=F_r\) for each \(r>0\) and \(\check{V}(E)=\check{V}(F)\) as \(\check{V}\) is non-atomic. For small \(r>0\),
as \(r\downarrow 0\). The result for general E as in the statement follows from the property that the closed intervals in \(\overline{E}\) are separated by open sets.\(\square \)
For \(p\in (0,V(B))\) we may write
where \(\check{J}=\check{g}\circ \check{F}^{-1}\). Note that \(\check{J}=J\) due to the fact that \(\check{F}\circ R=F\) on B.
Lemma 7.2
Let E be an \(\mathscr {L}^1\)-measurable set in \(\check{B}\). Then \(\check{V}(E_r)\ge \check{V}((E^\star )_r)\) for each \(r>0\). In particular, the rearrangement \(\cdot ^\star \) is smoothing in the sense that \((E^\star )_r\subset (E_r)^\star \) for each \(\mathscr {L}^1\)-measurable set E in \(\check{B}\) and \(r>0\).
Proof
We verify the conditions in [3, Theorem 2.1 (c)]. The measure \(\check{V}\) is a separable non-atomic Borel measure on the metric space \((\check{B},d)\). The r-neighbourhood (\(r>0\)) of any open ball in \(\check{B}\) is an open ball in \(\check{B}\). Let E be a finite union of open intervals in \((\check{B},d)\). By Lemma 7.1 and Corollary 6.11,
Thus by [3, Theorem 2.1], \(\check{V}(E_r)\ge \check{F}(\check{F}^{-1}(\check{V}(E))+r)= \check{V}((E^\star )_r)\) for any Borel set E in \(\check{B}\) with \(0<\check{V}(E)<V(B)\) and \(r>0\). The result then extends to \(\mathscr {L}^1\)-measurable sets in \(\check{B}\).\(\square \)
Lemma 7.3
Let A, E be \(\mathscr {L}^1\)-measurable sets in \(\check{B}\) with \(A\subset E\). Then \(d(A^\star ,\check{B}\setminus E^\star )\ge d(A,\check{B}\setminus E)\).
Here, \(d(A,E):=\inf \{d(x,y):x\in A,y\in E\}\) with the understanding that \(\inf \emptyset =+\infty \).
Proof
We use the criterion that for \(r>0\), \(A_r\subset E\) if and only if \(d(A,\check{B}\setminus E)\ge r\). Put \(r:=d(A,\check{B}\setminus E)\); we may assume that \(r>0\). By the criterion, \(A_r\subset E\) and hence \((A_r)^\star \subset E^\star \). By Lemma 7.2, \(\check{V}((A_r)^\star )=\check{V}(A_r)\ge \check{V}((A^\star )_r)\) meaning \((A^\star )_r\subset (A_r)^\star \subset E^\star \) which entails that \(d(A^\star ,\check{B}\setminus E^\star )\ge r\) by the criterion. \(\square \)
The modulus of continuity of an arbitrary real-valued function u on \(\check{B}\) is defined by
Observe that u is uniformly continuous on \(\check{B}\) if and only if \(\lim _{t\downarrow 0}\omega _u(t)=0\). We state the following criterion without proof.
Lemma 7.4
Let u be a real-valued function on \(\check{B}\) and \(t,\tau >0\). Then \(\omega _u(t)>\tau \) if and only if there exist \(s,s^\prime \in \mathbb {R}\) with \(s>s^\prime +\tau \) such that \(d(\{u>s\},\check{B}\setminus \{u>s^\prime \})<t\).
Proposition 7.5
Assume (A.1)–(A.5).
-
(i)
Let u be a real-valued \(\mathscr {L}^1\)-measurable function on \(\check{B}\). Then \(\omega _u(t)\ge \omega _{u^\star }(t)\) for each \(t>0\).
-
(ii)
If u is uniformly continuous on \(\check{B}\) then so is \(u^\star \).
-
(iii)
If u is Lipschitz continuous on \(\check{B}\) then so is \(u^\star \) and \(\mathrm {Lip}(u^\star ,\check{B})\le \mathrm {Lip}(u,\check{B})\).
Proof
Let \(t>0\). We may assume that \(\omega _{u^\star }(t)>0\). Choose \(\tau >0\) such that \(\omega _{u^\star }(t)>\tau \). By Lemma 7.4 there exist \(s,s^\prime \in \mathbb {R}\) with \(s>s^\prime +\tau \) such that \(d(\{u^\star >s\},\check{B}\setminus \{u^\star >s^\prime \})<t\). Now \(\{u^\star >s\}=\{|u|>s\}^\star \) and likewise for \(s^\prime \) by the counterpart of the equimeasurabilty property (6.4). By Lemma 7.3 we deduce that \(d(\{|u|>s\},\check{B}\setminus \{|u|>s^\prime \})<t\) and again by Lemma 7.4 that \(\omega _{u}(t)\ge \omega _{|u|}(t)>\tau \). Item (i) then follows. Part (ii) is a ready consequence. As for (iii),
\(\square \)
Let u be a Lipschitz continuous function on \((\check{B},d)\). By Rademacher’s theorem (cf. [1, Theorem 2.14]) u is differentiable \(\mathscr {L}^1\)-a.e. on \(\check{B}\) and its derivative coincides with the weak derivative on a set of full measure. Put
By [1, Lemmas 2.95 and 2.96], \(Z\cap \{u=t\}=\emptyset \) for \(\mathscr {L}^1\)-a.e. \(t\in \mathbb {R}\) and hence \(N:=u(Z)\subset \mathbb {R}\) is \(\mathscr {L}^1\)-negligible. The analogous sets corresponding to \(u^\star \) will be decorated with the subscript \(\star \).
We shall make use of the coarea formula [1, Theorem 2.93 and (2.74)],
for any \(\mathscr {L}^1\)-measurable function \(\phi :\,\check{B}\rightarrow [0,\infty ]\).
Lemma 7.6
Let u be a nonnegative Lipschitz continuous function on \((\check{B},d)\). Then
-
(i)
\(\check{\mu }_{u}\in \mathrm {BV}(\mathbb {R})\);
-
(ii)
\(D\check{\mu }_{u}=-u_\sharp \check{V}\);
-
(iii)
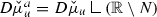 ;
; -
(iv)
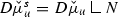 ;
; -
(v)
\(A:=\Big \{t\in \mathbb {R}:\mathscr {L}^1(Z\cap \{u=t\})>0\Big \}\) is the set of atoms of \(D\check{\mu }_{u}\) and
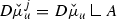 ;
; -
(vi)
\(\check{\mu }_u\) is differentiable \(\mathscr {L}^1\)-a.e. on \(\mathbb {R}\) with derivative given by
$$\begin{aligned} \check{\mu }_{u}^\prime (t)=-\int _{(\check{B}\setminus Z)\cap \{u=t\}}\frac{\check{g}}{|u^\prime |}\,d\mathcal {H}^{0} \end{aligned}$$for \(\mathscr {L}^1\)-a.e. \(t\in \mathbb {R}\);
-
(vii)
\(\mathrm {Ran}(u)=\mathrm {supp}(D\check{\mu }_u)\).
The notation above \(D\check{\mu }_{u}^a\), \(D\check{\mu }_{u}^s\), \(D\check{\mu }_{u}^j\) stands for the absolutely continuous resp. singular resp. jump part of the measure \(D\check{\mu }_{u}\) (see [1, 3.2] for example).
Proof
For any \(\varphi \in C^\infty _c(\mathbb {R})\),
by Fubini’s theorem; so \(\check{\mu }_{u}\in \mathrm {BV}(\mathbb {R})\) and \(D\check{\mu }_{u}\) is the push-forward of \(\check{V}\) under u, \(D\check{\mu }_{u}=-u_\sharp \check{V}\) (cf. [1, 1.70]). By (7.1),

for any \(\mathscr {L}^1\)-measurable set A in \(\mathbb {R}\). In light of the above, we may identify  and
and  . The set of atoms of \(D\check{\mu }_{u}\) is defined by \(A:=\{t\in \mathbb {R}:D\check{\mu }_{u}(\{t\})\ne 0\}\). By [13, Lemma 7.7], we may write A as in (v). The monotone function \(\check{\mu }_u\) is a good representative within its equivalence class and is differentiable \(\mathscr {L}^1\)-a.e. on \(\mathbb {R}\) with derivative given by the density of \(D\check{\mu }_{u}\) with respect to \(\mathscr {L}^1\) by [1, Theorem 3.28]. Item (vii) follows from (ii).\(\square \)
. The set of atoms of \(D\check{\mu }_{u}\) is defined by \(A:=\{t\in \mathbb {R}:D\check{\mu }_{u}(\{t\})\ne 0\}\). By [13, Lemma 7.7], we may write A as in (v). The monotone function \(\check{\mu }_u\) is a good representative within its equivalence class and is differentiable \(\mathscr {L}^1\)-a.e. on \(\mathbb {R}\) with derivative given by the density of \(D\check{\mu }_{u}\) with respect to \(\mathscr {L}^1\) by [1, Theorem 3.28]. Item (vii) follows from (ii).\(\square \)
Lemma 7.7
Let u be a nonnegative Lipschitz continuous function on \((\check{B},d)\). Then \(\int _{\check{B}\cap Z}u^2\,d\check{V}=\int _{\check{B}\cap Z_\star }(u^\star )^2\,d\check{V}\).
Proof
As Z has finite \(\mathscr {L}^1\)-measure, \(A\subset \mathbb {R}\) is a countable set. Thus
and an analogous result holds for \(u^\star \) by Lemma 7.6. The fact that \(\check{\mu }_u=\check{\mu }_{u^\star }\) entails that \(A=A_\star \). This leads to the result. \(\square \)
Theorem 7.8
Assume (A.1)–(A.5). Let u be a Lipschitz continuous function on \((\check{B},d)\). Then \(u,u^\star \in D(\check{\mathscr {E}})\) and \(\check{\mathscr {E}}(u,u)\ge \check{\mathscr {E}}(u^\star ,u^\star )\).
Proof
Given a Lipschitz continuous function u on \((\check{B},d)\), \(u\in W^{1,\infty }(\check{B})\) and \(\Vert u^\prime \Vert _{L^\infty (\check{B})}=\mathrm {Lip}(u,\check{B})\) (see [1, Proposition 2.13]) so \(u\in D(\check{\mathscr {E}})\). The same is true for \(u^\star \) by Proposition 7.5. Replacing u by |u| and using the contraction property of the Dirichlet form \((D(\check{\mathscr {E}}),\check{\mathscr {E}})\) we may assume that u is nonnegative.
The proof hinges on the identity
which is a consequence of the coarea formula (7.1).
As \(\check{\mu }_u=\check{\mu }_{u^\star }\) we have that \(D\check{\mu }_u=D\check{\mu }_{u^\star }\). In particular, we derive that
for \(\mathscr {L}^1\)-a.e. \(t\in \mathbb {R}\) by Lemma 7.6.
Let \(t\in \mathrm {Ran}(u)\) be such that \(Z\cap \{u=t\}=\emptyset \) and \(\int _{({\check{B}\setminus Z})\cap \{u=t\}}\check{g}\,d\mathcal {H}^{0}<\infty \) and the analogous properties hold for \(u^\star \). We assume in addition that (7.3) holds. Such t comprise a set of full measure in the range of u. Then \(\partial \{u>t\}=\check{B}\cap \{u=t\}\cup \partial \check{B}\cap \partial \{u>t\}\) and \(\{u>t\}\) is a Caccioppoli set in \(\check{B}\) with finite \(\check{g}\)-perimeter; and likewise for \(u^\star \). From Corollary 6.11,
Moreover, \(\check{B}\cap \{u^\star =t\}\) consists of a singleton; thus,
where Jensen’s inequality has been used in the first inequality and (7.4) in the second. This inequality combined with (7.2) as well as Lemma 7.7 lead to the result. \(\square \)
Corollary 7.9
Let \(u\in D(\check{\mathscr {E}})\). Then \(u^\star \in D(\check{\mathscr {E}})\) and \(\check{\mathscr {E}}(u,u)\ge \check{\mathscr {E}}(u^\star ,u^\star )\).
Proof
Let \(u\in D(\check{\mathscr {E}})\). By Lemma 5.5 we may choose a sequence \((u_h)\) in \(C^\infty (\overline{\check{B}})\) that converges to u in \((D(\check{\mathscr {E}}),\check{\mathscr {E}})\); each \(u_h\) is Lipschitz continuous on \(\check{B}\). By Theorem 6.13, \((u^\star _h)\) converges to \(u^\star \) in \(L^2(\check{B},\check{V})\). By Theorem 7.8, each \(u^\star _h\in D(\check{\mathscr {E}})\) and \(\check{\mathscr {E}}(u^\star _h,u^\star _h)\le \check{\mathscr {E}}(u_h,u_h)\), so the sequence \((\check{\mathscr {E}}(u^\star _h,u^\star _h))_h\) is uniformly bounded in \(\mathbb {R}\). By the Banach-Alaoglu theorem (cf. [19, A2 Theorem 2.1]) we may assume that \(u^\star _h\rightarrow v\) weakly as \(h\rightarrow \infty \) in \((D(\check{\mathscr {E}}),\check{\mathscr {E}})\) for some \(v\in D(\check{\mathscr {E}})\) by selecting a subsequence if necessary. We may identify v with \(u^\star \) thanks to the \(L^2(\check{B},\check{V})\) convergence and the Banach-Saks theorem (cf. [19, A2 Theorem 2.2]); hence \(u^\star \in D(\check{\mathscr {E}})\). By [16, Theorem 10.1.5],
\(\square \)
Corollary 7.10
Let \(u\in D(\hat{\mathscr {E}})\). Then \(u^\bigstar \in D(\hat{\mathscr {E}})\) and \(\hat{\mathscr {E}}(u,u)\ge \hat{\mathscr {E}}(u^\bigstar ,u^\bigstar )\).
Proof
Let \(u\in D(\hat{\mathscr {E}})\). Then \(v:=u\circ R^{-1}\in D(\check{\mathscr {E}})\) by Lemma 5.5. Morever, \(u^\bigstar =v^\star \circ R\) by Proposition 6.10. By Lemma 5.5 and Corollary 7.9,
\(\square \)
8 Equality Case in the Pólya–Szegö Inequality
We now investigate the equality case in the Pólya–Szegö inequality.
Lemma 8.1
Let \(u\in D(\check{\mathscr {E}})\) and \(t\in \mathbb {R}\).
-
(i)
Put \(v:=u\wedge t\). Then \(\int _{\check{B}}|v^\prime |^2\,d\check{V}=\int _{\check{B}\cap \{u>t\}}|u^\prime |^2\,d\check{V}=\int _{\check{B}\cap \{u\ge t\}}|u^\prime |^2\,d\check{V}\).
-
(ii)
Put \(v:=u\vee t\). Then \(\int _{\check{B}}|v^\prime |^2\,d\check{V}=\int _{\check{B}\cap \{u<t\}}|u^\prime |^2\,d\check{V}=\int _{\check{B}\cap \{u\le t\}}|u^\prime |^2\,d\check{V}\).
Proof
We only prove (i). Write
The set \(\{u<t\}\) is open in \(\check{B}\) as u is continuous so \(v=u\) and \(v^\prime =u^\prime \) there. By [13, Lemma 7.7], \(v^\prime =0\) \(\mathscr {L}^1\)-a.e. on \(\{u\ge t\}\).\(\square \)
Suppose that \(u\in W^{1,2}_{\mathrm {loc}}(\check{B})\) is precisely represented in the sense of [18, (2.5)]. Then the set \(\{u=t\}\) is finite or countably infinite for \(\mathscr {L}^1\)-a.e. \(t\in \mathbb {R}\) and the coarea formula (7.1) holds for u by [18, Theorem 1.1]. With Z as before it follows that \(Z\cap \{u=t\}=\emptyset \) for \(\mathscr {L}^1\)-a.e. \(t\in \mathbb {R}\) and hence \(N:=u(Z)\subset \mathbb {R}\) is \(\mathscr {L}^1\)-negligible.
Lemma 8.2
Let u be a nonnegative function in \(W^{1,2}_{\mathrm {loc}}(\check{B})\) precisely represented in the sense of [18, (2.5)]. Then statements (i)–(vii) of Lemma 7.6 hold.
Proof
This runs as in Lemma 7.6. \(\square \)
Lemma 8.3
Let \(u\in D(\check{\mathscr {E}})\) be nonnegative. Then \(\int _{\check{B}\cap Z}u^2\,d\check{V}=\int _{\check{B}\cap Z_\star }(u^\star )^2\,d\check{V}\).
Proof
The proof proceeds as in Lemma 7.7. \(\square \)
Lemma 8.4
Let \(u\in D(\check{\mathscr {E}})\) be nonnegative. Then
-
(i)
for \(t^\prime ,t^{\prime \prime }\in \mathbb {R}\) with \(0\le t^\prime <t^{\prime \prime }\),
$$\begin{aligned} \int _{\check{B}\cap \{t^\prime <u\le t^{\prime \prime }\}}\Big (u^2+|u^\prime |^2\Big )\,d\check{V} \ge \int _{\check{B}\cap \{t^\prime <u\le t^{\prime \prime }\}}\Big ((u^\star )^2+|(u^\star )^\prime |^2\Big )\,d\check{V}; \end{aligned}$$ -
(ii)
for \(\mathscr {L}^1\)-a.e. \(t\in \mathbb {R}\),
$$\begin{aligned} \int _{(\check{B}\setminus Z)\cap \{\tilde{u}=t\}}\frac{\tilde{u}^2+|\tilde{u}^\prime |^2}{|\tilde{u}^\prime |}\check{g}\,d\mathcal {H}^0 \ge \int _{(\check{B}\setminus Z_\star )\cap \{u^\star =t\}}\frac{(u^\star )^2+|(u^\star )^\prime |^2}{|(u^\star )^\prime |}\check{g}\,d\mathcal {H}^0 \end{aligned}$$where \(\tilde{u}\) is the unique continuous representative of u (cf. [1, Definition 3.31 and after]).
Proof
(i) Put \(v:=(u\vee t^\prime )\wedge t^{\prime \prime }\in D(\check{\mathscr {E}})\). By Lemma 8.1,
By Lemma 10.2, \(\check{v}^\sharp =(\check{u}^\sharp \vee t^\prime )\wedge t^{\prime \prime }\) on \([0,\check{V}(\check{B})]\) and hence \(v^\star =(u^\star \vee t^\prime )\wedge t^{\prime \prime }\). We may then write an identity of the above form but with \(u^\star ,v^\star \) in place of u, v. The statement then follows from Corollary 7.9.
(ii) Note that \(\tilde{u}\) is precisely represented in the sense of [18, (2.5)]. By the coarea formula for Sobolev mappings [18, Theorem 1.1],
for any \(\mathscr {L}^1\)-measurable function \(\phi :\check{B}\rightarrow [0,\infty ]\). In particular,
for any \(\mathscr {L}^1\)-measurable function \(\phi :\mathbb {R}\rightarrow [0,\infty ]\).
Define
for \(t\in \mathbb {R}\). For \(\varphi \in C^\infty _c(\mathbb {R},\mathbb {R})\),
so that \(w\in \mathrm {BV}(\mathbb {R})\). By (8.1), \(Dw=\rho \mathscr {L}^1\) where
for \(t\in \mathbb {R}\); that is, w is absolutely continuous [1, Definition 3.31]. By [1, Theorem 3.28], w is differentiable \(\mathscr {L}^1\)-a.e. on \(\mathbb {R}\) and \(w^\prime =\rho \) \(\mathscr {L}^1\)-a.e. on \(\mathbb {R}\). The same holds for the function \(w_\star \) defined as for w but with \(u^\star \) in place of u. Note that \(\widetilde{u^\star }=u^\star \). The statement then follows from (i).\(\square \)
We state the following lemma without proof.
Lemma 8.5
Let u be a continuous real-valued function on \(\check{B}\). Suppose that for \(\mathscr {L}^1\)-a.e. \(t>0\) the set \(\{u>t\}\) is either an open interval in \(\check{B}\) abutting a boundary point or \(\{u>t\}=\emptyset \). Then u is monotone on \(\check{B}\).
Theorem 8.6
Let \(u\in D(\check{\mathscr {E}})\) be nonnegative and suppose that \(\check{\mathscr {E}}(u,u)=\check{\mathscr {E}}(u^\star ,u^\star )\). Then \(\tilde{u}\) is monotone on \(\check{B}\).
Proof
By (8.1),
and a similar identity holds for \(u^\star \). We may assume that \(\mathrm {Ran}(\tilde{u})\) is a closed interval in \([0,\infty )\) with non-empty interior. By Lemmas 8.3 and 8.4,
for \(\mathscr {L}^1\)-a.e. \(t\in \mathrm {Ran}(\tilde{u})\). The chain of inequalities in (7.6) is valid with \(\tilde{u}\) in place of u and we may replace the sign \(\ge \) with the equality sign. In particular,
for \(\mathscr {L}^1\)-a.e. \(t\in \mathrm {Ran}(\tilde{u})\). Suppose that \(t\in \mathrm {Ran}(\tilde{u})\) such that \(Z\cap \{\tilde{u}=t\}=\emptyset \) and \(\int _{\check{B}\cap \{\tilde{u}=t\}}\check{g}\,d\mathcal {H}^{0}<\infty \). We remark that \(\partial \{\tilde{u}>t\}=\check{B}\cap \{\tilde{u}=t\}\cup \partial \check{B}\cap \partial \{\tilde{u}>t\}\) and \(\{\tilde{u}>t\}\) is a Caccioppoli set in \(\check{B}\) with finite \(\check{g}\)-perimeter \(P_{\check{g}}(\{\tilde{u}>t\},\check{B})=\int _{\check{B}\cap \{\tilde{u}=t\}}\check{g}\,d\mathcal {H}^0<\infty \). From the identity (8.2) we derive that \(P_{\check{g}}(\{\tilde{u}>t\},\check{B})=P_{\check{g}}(\{u^\star >t\},\check{B})\) for \(\mathscr {L}^1\)-a.e. \(t\in \mathrm {Ran}(\tilde{u})\). By Corollary 6.12 the set \(\{\tilde{u}>t\}\) is either an open interval in \(\check{B}\) abutting a boundary point or \(\{\tilde{u}>t\}=\emptyset \) for \(\mathscr {L}^1\)-a.e. \(t>0\). The statement follows by Lemma 8.5.\(\square \)
Corollary 8.7
Let \(u\in D(\hat{\mathscr {E}})\) be nonnegative and suppose that \(\hat{\mathscr {E}}(u,u)=\hat{\mathscr {E}}(u^\bigstar ,u^\bigstar )\). Then \(\tilde{u}\) is monotone on B.
Proof
Put \(v:=u\circ R^{-1}\in D(\check{\mathscr {E}})\) by Lemma 5.5. Also, \(u^\bigstar =v^\star \circ R\) by Proposition 6.10. We have
by Lemma 5.5 and Corollary 7.9. So \(\check{\mathscr {E}}(v,v)=\check{\mathscr {E}}(v^\star ,v^\star )\). By Theorem 8.6, \(\tilde{v}\) is monotone on \(\check{B}\) and hence \(\tilde{u}\) is monotone on B.\(\square \)
9 Application to Exchange Flow
Consider the positive definite bilinear form \((\mathscr {D},\mathscr {E})\) in \(L^2(B,\mathscr {L}^1)\) given by

Here, \(\psi :=u_B\) is given by \(\psi (x)=(1/2)(1-|x|^2)\) for \(x\in B\).
Lemma 9.1
-
(i)
\((\mathscr {D},\mathscr {E})\) is closable in \(L^2(B,\,\mathscr {L}^1)\) with closure denoted \((D(\mathscr {E}),\,\mathscr {E})\);
-
(ii)
\((D(\mathscr {E}),\,\mathscr {E})\) is a symmetric Dirichlet form in \(L^2(B,\,\mathscr {L}^1)\);
-
(iii)
\(D(\mathscr {E})=W^{1,2}_0(B)\).
Proof
(i) Suppose \((u_h)\) is a sequence in \(\mathscr {D}\) such that \(u_h\rightarrow 0\) in \(L^2(B,\mathscr {L}^1)\). We write \(v\in \mathscr {D}\) in the form \(v=\psi w\) for some \(w\in C^\infty (\overline{B})\); so \(v^{\prime \prime }\in L^2(B,\mathscr {L}^1)\). An integration-by-parts gives
as \(h\rightarrow \infty \) where \(\nu =\pm 1\) is the unit exterior normal on \(\partial B\). The statement follows by [19, Lemma I.3.4]. Then \((D(\mathscr {E}),\mathscr {E})\) is a symmetric closed form by definition (cf. [19, Definition I.2.3]). By [19, Proposition I.4.10 and II.2 (c)], \((D(\mathscr {E}),\mathscr {E})\) is a symmetric Dirichlet form and (ii) follows. Note that \(\psi =u_B\in W^{1,2}_0(B)\). Thus \(C^\infty _0(B)\subset \mathscr {D}\subset W^{1,2}_0(B)\). This proves (iii).\(\square \)
The transient Dirichlet space \((D(\mathscr {E}),\mathscr {E})\) has reference function \(\psi ^{-1}\) and
Denote by \(D(\mathscr {E})_e\) the extended Dirichlet space; that is, the family of \(\mathscr {L}^1\)-measurable functions u on B such that \(|u|<\infty \) \(\mathscr {L}^1\)-a.e. and there exists an \(\mathscr {E}\)-Cauchy sequence \((u_h)\) of functions in \(D(\mathscr {E})\) such that \(u_h\rightarrow u\) \(\mathscr {L}^1\)-a.e. on B. By [12, Lemma 1.5.5], \((D(\mathscr {E})_e,\mathscr {E})\) is a Hilbert space. The identity (9.1) extends to \(D(\mathscr {E})_e\) and \(D(\mathscr {E})_e\subset L^1(B,\psi ^{-1}\mathscr {L}^1)\).
In the notation of Sect. 5 we take \(f=\psi \) and \(g=\psi ^{3/2}\). The conditions (A.1)–(A.5) are satisfied by Proposition 6.5. Let V be the measure \(V:=\psi \mathscr {L}^1\) on B. We work with the symmetric Dirichlet form

in \(L^2(B,V)\) with domain
Proposition 9.2
The bijective mapping \(\mathscr {D}\rightarrow C^\infty (\overline{B});\,u\mapsto \overline{u}:=u/\psi \) extends to a Hilbert space isomorphism \(E:D(\mathscr {E})_e\rightarrow D(\hat{\mathscr {E}})\). In particular, for \(u,v\in D(\mathscr {E})_e\) we have that
Proof
Using integration-by-parts and the fact that \(-\psi ^{\prime \prime }=1\) on B gives
where \(\nu =\pm 1\) is the unit exterior normal on \(\partial B\). This establishes (9.2) on \(\mathscr {D}\). The map E extends to \(D(\mathscr {E})\) by density of \(\mathscr {D}\) in \(D(\mathscr {E})\) as does (9.2). Let \(u\in D(\mathscr {E})_e\) and choose a sequence \((u_h)\) in \(D(\mathscr {E})\) such that \(u_h\rightarrow u\) \(\mathscr {L}^1\)-a.e. on B as \(h\rightarrow \infty \) and \((u_h)\) is a \(\mathscr {E}\)-Cauchy sequence. Then \((\overline{u}_h)\) is a Cauchy sequence in \((D(\hat{\mathscr {E}}),\hat{\mathscr {E}})\) with limit \(v\in D(\hat{\mathscr {E}})\) say. Define \(Eu:=v\). This definition is well-defined and the identity (9.2) holds on \(D(\mathscr {E})_e\). In particular, the mapping E is injective.
We show that E is a surjection. Let \(v\in D(\hat{\mathscr {E}})\). We put \(u:=\psi v\) and claim that \(u\in D(\mathscr {E})_e\). Then there exists a sequence \((w_h)\) in \(C^\infty (\overline{\check{B}})\) such that \(v_h:=w_h\circ R\rightarrow v\) in \((D(\hat{\mathscr {E}}),\hat{\mathscr {E}})\) as \(h\rightarrow \infty \). Put \(u_h:=\psi v_h\) for each h. Now \(u_h\in C^1(\overline{B})\) and \(u_h=0\) on \(\partial B\) for each h. This means that \((u_h)\) is a sequence in \(D(\mathscr {E})\). By (9.2), \((u_h)\) is a \(\mathscr {E}\)-Cauchy sequence. As \((v_h)\) converges to v in \(L^2(B,V)\) we may assume that \((v_h)\) converges to v V-a.e. on B by selecting a subsequence if necessary. Thus, \((u_h)\) converges to u \(\mathscr {L}^1\)-a.e. on B. This shows that \(u\in D(\mathscr {E})_e\) and \(Eu=v\).\(\square \)
Theorem 9.3
For any \(\mathscr {L}^1\)-measurable set A in B, \(J(A)\le J(A^\bigstar )\).
Proof
Let A be an \(\mathscr {L}^1\)-measurable set in B and put \(u:=u_A\in D(\mathscr {E})\) and \(v:=u_{A^\bigstar }\in D(\mathscr {E})\). By Theorem 6.6, Proposition 9.2, the Cauchy–Schwarz inequality and Corollary 7.10,
and the result follows.\(\square \)
Theorem 9.4
Suppose that A is an \(\mathscr {L}^1\)-measurable set in B such that \(J(A)= J(A^\bigstar )\). Then A is \(\mathscr {L}^1\)-a.e. equivalent to an open interval in B abutting a boundary point of B.
Proof
We may assume that \(0<V(A)<V(B)\). From the chain of inequalities in the proof of Theorem 9.3 we derive that \(\hat{\mathscr {E}}(\overline{u}^\bigstar ,\overline{u}^\bigstar )=\hat{\mathscr {E}}(\overline{u},\overline{u})\). Put \(v:=\overline{u}\). From Corollary 8.7 we infer that \(\widetilde{v}\) is monotone on B. Put \(p:=V(A)/V(B)\in (0,1)\). By Theorem 9.3, A is an optimal configuration for the problem (1.2) for the data (B, p). By Proposition 3.3, \(V(A\Delta \{\widetilde{v}>c\})=0\) for some \(c\in (0,1)\). As \(\widetilde{v}\) is monotone, \(\{\widetilde{v}>c\}\) is an open interval in B abutting an end-point of B. This leads to the result.\(\square \)
We may now characterise optimal configurations for the problem (1.2).
Theorem 9.5
Let \(p\in (0,1)\).
-
(i)
The sets \((-1,F^{-1}(pV(B)))\) and \((F^{-1}((1-p)V(B)),1)\) are optimal configurations for the problem (1.2) with data (B, p).
-
(ii)
If \(E\subset B\) is an optimal configuration for the data (B, p) then E is \(\mathscr {L}^1\)-a.e. equivalent to one of the sets in (i).
Let U be a bounded open connected set in \(\mathbb {R}^n\) (\(n\ge 1\)).
Proposition 9.6
-
(i)
For \(\lambda \in (-1,1)\), \(\gamma (U,\lambda ) = 2 I(U,p)\) where \(p=(1-\lambda )/2\).
-
(ii)
\(\gamma (U) = 2\sup _{p\in (0,1)} I(U,p)\).
Proof
(i) Let A be an open set in U. Suppose u satisfies (1.3) and the condition \((u,1)=0\). Put \(f:=-(\lambda + 1)\chi _A-(\lambda - 1) \chi _{U\setminus A}\); then \(u=Gf\). From the flux-balance condition and symmetry of the Green operator,
So \(\lambda = V(U)^{-1}\{V(U\setminus A)-V(U)\}\) and \(V(A) = \frac{1-\lambda }{2}V(U)\). We have
where \(p=(1-\lambda )/2\). This leads to the reformulation (i). (ii) follows immediately.\(\square \)
Recall that for \(x,y\in B\),
Lemma 9.7
The mapping \((0,1)\rightarrow \mathbb {R};p\rightarrow I(B,p)\) has a unique global maximum at \(p=1/2\).
Proof
Define \(\eta :B\rightarrow \mathbb {R}\) by \(\eta =J(A)-V(B)^{-1}V(A)^2\) where \(A=(-1,t)\). Then \(I(B,p)=\eta (F^{-1}(pV(B)))\) for \(p\in (0,1)\) by Theorem 9.5. For \(t\in B\),
so that
A further computation gives
We then obtain that \(\eta ^\prime (t)=-(1/4)t(1-t^2)^2\) for any \(t\in B\). This proves the result.\(\square \)
Theorem 9.8
Let \(\lambda \in (-1,1)\).
-
(i)
The sets \((-1,F^{-1}(pV(B)))\) and \((F^{-1}((1-p)V(B)),1)\) are optimal configurations for the problem (1.5) with data \((U,\lambda )\) where \(p=(1-\lambda )/2\).
-
(ii)
If \(E\subset B\) is an optimal configuration for the problem (1.5) with data \((U,\lambda )\) then E is \(\mathscr {L}^1\)-a.e. equivalent to one of the sets in (i).
-
(iii)
The sets \((-1,0)\) and (0, 1) are optimal configurations for the problem (1.4).
-
(iv)
If \(E\subset B\) is an optimal configuration for the problem (1.4) then E is \(\mathscr {L}^1\)-a.e. equivalent to one of the sets in (iii).
Proof
Parts (i) and (ii) follow from Proposition 9.6 and Theorem 9.5. (iii) and (iv) follow from Proposition 9.6 and Lemma 9.7. \(\square \)
References
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford University Press, Oxford (2000)
Betta, F.M., Brock, F., Mercaldo, A., Posteraro, M.R.: Weighted isoperimetric inequalities on \(\mathbb{R}^n\) and applications to rearrangements. Math. Nachr. 281(4), 466–498 (2008)
Bobkov, S.G., Houdré, C.: Some Connections Between Sobolev-Type Inequalities and Isoperimetry. AMS, Providence (1997)
Brock, F., Solynin, A.Y.: An approach to symmetrisation via polarization. Trans. Am. Math. Soc. 352(4), 1759–1796 (1999)
Bourbaki, N.: Espaces Vectoriels Topologiques. Chapitres 1 à 5, Éléments de mathématique. Masson, Paris (1981)
Chanillo, S., Grieser, D., Imai, M., Kurata, K., Ohnishi, I.: Symmetry breaking and other phenomena in the optimization of eigenvalues for composite membranes. Commun. Math. Phys. 214, 315–337 (2000)
Chanillo, S., Grieser, D., Kurata, K.: The free boundary problem in the optimization of composite membranes. Differential Geometric Methods in the Control of Partial Differential Equations. AMS, Providence (2000)
Cox, J.C., McLaughlin, J.R., Extremal eigenvalue problems for composite membranes, I, II, Appl. Math. Optim. 22, 153–167, 169–187 (1990)
Crowe, J.A., Zweibel, J.A., Rosenbloom, P.C.: Rearrangements of functions. J. Funct. Anal. 66, 432–438 (1986)
Evans, L.C.: Partial Differential Equations. AMS, Providence (1998)
Friedland, S.: Extremal eigenvalue problems defined for certain classes of functions. Arch. Ration. Mech. Anal. 67(1), 73–81 (1977)
Fukushima, M., Oshima, Y., Takeda, M.: Dirichlet Forms and Symmetric Markov Processes. Walter de Gruyter, Berlin (2011)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order. Springer, Berlin (1977)
Hardy, G.H., Littlewood, J.E., Pólya, G.: Inequalities. Cambridge University Press, Cambridge (1934)
Kerswell, R.: Exchange flow of two immiscible fluids and the principle of maximum flux. J. Fluid Mech. 682, 132–159 (2011)
Lax, P.: Functional Analysis. Wiley, New York (2002)
Lieb, E., Loss, M.: Analysis. AMS, Providence (1997)
Malý, J., Swanson, D., Ziemer, W.P.: The coarea formula for Sobolev mappings. Trans. AMS 355(2), 477–492 (2002)
Ma, Z.-M., Röckner, M.: Introduction to the Theory of (Non-symmetric) Dirichlet Forms. Springer, Berlin (1992)
Petrosyan, A., Shahgholian, H., Uraltseva, N.: Regularity of Free Boundaries in Obstacle-Type Problems. AMS, Providence (2012)
Sarvas, J.: Symmetrization of condensers in \(n\)-space. Ann. Acad. Sci. Fenn. Ser. A1(522), 1–44 (1972)
Talenti, G.: A weighted version of a rearrangement inequality. Ann. Univ. Ferrara - Sez. VII - Sc. Mat. XLIII, 121–133 (1997)
van Schaftingen, J.: Universal approximation of symmetrizations by polarizations. Proc. Am. Math. Soc. 134(1), 177–186 (2005)
Author information
Authors and Affiliations
Corresponding author
Appendix: On the Generalised Inverse Function
Appendix: On the Generalised Inverse Function
Let \((X,\mathscr {A},\mu )\) be a finite measure space. Let \(f:X\rightarrow [0,\infty )\) be an \(\mathscr {A}\)-measurable function. The distribution function \(\mu _f:[0,\infty )\rightarrow [0,\mu (X)]\) of f is defined by \(\mu _f(t):=\mu (\{f>t\})\) for \(t\ge 0\). Note that \(\mu _f\) is right-continuous and non-increasing on \([0,\infty )\) and \(\mu _f(t)\rightarrow 0\) as \(t\rightarrow \infty \). The generalised inverse \(f^\sharp :[0,\mu (X)]\rightarrow [0,\infty ]\) of \(\mu _f\) is defined by \(f^\sharp (s):=\inf \{t\ge 0:\mu _f(t)\le s\}\) with the understanding that \(\inf \emptyset =+\infty \).
Lemma 10.1
Let \(f:X\rightarrow [0,\infty )\) be an \(\mathscr {A}\)-measurable function. Let \(t\ge 0\) and \(s\in [0,\mu (X)]\). Then
-
(i)
\(\mu _f(t)>s\) if and only if \(f^\sharp (s)>t\);
-
(ii)
\(\mu _f(t)\le s\) if and only if \(f^\sharp (s)\le t\);
-
(iii)
\(\mu _f(t-)<s\) then \(f^\sharp (s)<t\) in case \(t>0\).
Proof
Suppose \(\mu _f(t)>s\). The set \(\{\mu _f>s\}\subset [0,\infty )\) is relatively open by right-continuity of \(\mu _f\). It follows that \(f^\sharp (s)>t\). Conversely, if \(f^\sharp (s)>t\) then \(\mu _f(t)>s\) be definition of \(f^\sharp \). This shows (i). (ii) follows from (i). Suppose \(t>0\) and \(\mu _f(t-)<s\). By definition of the left-handed limit, we may choose \(0<\tau <t\) such that \(\mu _f(t-)\le \mu _f(\tau )<s\). Then \(f^\sharp (s)\le \tau <t\). This shows (iii). \(\square \)
Lemma 10.2
Let \(f:X\rightarrow [0,\infty )\) be an \(\mathscr {A}\)-measurable function and \(t>0\). Then
-
(i)
if \(g:=f\wedge t\) then \(g^\sharp =f^\sharp \wedge t\) on \([0,\mu (X))\);
-
(ii)
if \(g:=f\vee t\) then \(g^\sharp =f^\sharp \vee t\) on \([0,\mu (X))\).
Proof
(i) We have that \(\mu _g=\chi _{[0,t)}\mu _f\) on \([0,\infty )\) and \(g^\sharp =t\chi _{[0,\mu _f(t-))}+f^\sharp \chi _{[\mu _f(t-),\mu (X))}\). On the other hand, \(w:=f^\sharp \wedge t=f^\sharp \chi _{\{f^\sharp < t\}}+t\chi _{\{f^\sharp \ge t\}}\). Let \(0\le s<\mu _f(t-)\). As \(\mu _f\ge \mu _f(t-)>s\) on [0, t), \(\{\mu _f\le s\}\subset [t,\infty )\) and \(f^\sharp (s)\ge t\); that is, \(w(s)=t=g^\sharp (s)\). Now suppose that \(s=\mu _f(t-)\). Note that \(f^\sharp (s)\le t\). Consider the case that \(f^\sharp (s)=t\). Then \(w(s)=t=f^\sharp (s)=g^\sharp (s)\). If \(f^\sharp (s)<t\) then \(w(s)=f^\sharp (s)=g^\sharp (s)\). Finally, suppose that \(s>\mu _f(t-)\). By Lemma 10.1 (iii), \(w(s)=f^\sharp (s)=g^\sharp (s)\). Item (i) follows.
(ii) In this case, \(\mu _g=\chi _{[0,t)}+\chi _{[t,\infty )}\mu _f\) on \([0,\infty )\) and \(g^\sharp =\chi _{[0,\mu _f(t))}f^\sharp +t\chi _{[\mu _f(t),\mu (X))}\). On the other hand, \(w:=f^\sharp \vee t=t\chi _{\{f^\sharp \le t\}}+f^\sharp \chi _{\{f^\sharp >t\}}\). Let \(0\le s<\mu _f(t)\). By Lemma 10.1 (i), \(f^\sharp (s)>t\) and \(w(s)=f^\sharp (s)=g^\sharp (s)\). Now suppose that \(s\ge \mu _f(t)\). By Lemma 10.1 (ii), \(f^\sharp (s)\le t\) and \(w(s)=t=g^\sharp (s)\).\(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
McGillivray, I. An Unstable Two-Phase Membrane Problem and Maximum Flux Exchange Flow. Appl Math Optim 75, 365–401 (2017). https://doi.org/10.1007/s00245-016-9335-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00245-016-9335-7
Keywords
- Two-phase membrane problem
- Isoperimetric inequality
- Pólya–Szegö inequality
- Spherical cap symmetrisation



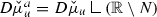 ;
;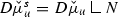 ;
;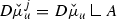 ;
;