Skip to main content
SpringerLink
Log in

Uniform Decay for Solutions of an Axially Moving Viscoelastic Beam

  • Published:
Applied Mathematics & Optimization Submit manuscript

Abstract

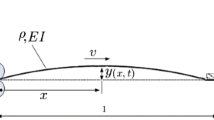
The paper deals with an axially moving viscoelastic structure modeled as an Euler–Bernoulli beam. The aim is to suppress the transversal displacement (transversal vibrations) that occur during the axial motion of the beam. It is assumed that the beam is moving with a constant axial speed and it is subject to a nonlinear force at the right boundary. We prove that when the axial speed of the beam is smaller than a critical value, the dissipation produced by the viscoelastic material is sufficient to suppress the transversal vibrations. It is shown that the rate of decay of the energy depends on the kernel which arise in the viscoelastic term. We consider a general kernel and notice that solutions cannot decay faster than the kernel.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1

Similar content being viewed by others

References

  1. Choi, J.Y., Hong, K.S., Yang, K.J.: Exponential stabilization of an axially moving tensioned strip by passive damping and boundary control. J. Vib. Acoust. 10(5), 661–682 (2004)

    MathSciNet  MATH  Google Scholar 

  2. Coleman, B.D., Noll, W.: Foundations of linear viscoelasticity. Rev. Mod. Phys. 33, 239–249 (1961)

    Article  MathSciNet  MATH  Google Scholar 

  3. Coleman, B.D., Mizel, V.J.: On the general theory of fading memory. Arch. Ration. Mech. Anal. 29, 18–31 (1968)

    MathSciNet  MATH  Google Scholar 

  4. Coron, J.M., d’Andrea-Novel, B.: Stabilization of a rotating rody beam without damping. IEEE Trans. Auto. Control 43(5), 608–619 (1998)

    Article  MATH  Google Scholar 

  5. Dafermos, C.M.: On abstract Volterra equations with applications to linear viscoelasticity. J. Differ. Equ. 7, 554–569 (1970)

    Article  MathSciNet  MATH  Google Scholar 

  6. Fabrizio, M., Morro, A.: Mathematical Problems in Linear Viscoelasticity. SIAM Stud. Appl. Math. Philadelphia (1992)

  7. Guo, B.Z., Chan, K.Y.: Riesz basis generation eigenvalues distribution and exponential stability for an Euler-Bernoulli beam with joint feedback control. Rev. Mat. Complut. XIV(1), 295–229 (2001)

  8. Guo, B.Z., Guo, W.: Stabilization and parameter estimation for an Euler–Bernoulli beam equation with uncertain harmonic disturbance under boundary output feedback control. Nonlinear Anal. 61, 671–693 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  9. Guo, F., Huang, F.: Boundary feedback stabilization of the undamped Euler-Bernoulli beam with both ends free. SIAM J. Control Optim. 43(1), 341–356 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  10. Guo, B.Z., Song, Q.: Tracking control of a flexible beam by nonlinear boundary feedback. J. Appl. Math. Stoch. Anal. 8(1), 47–58 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  11. Hardy, G.H., Littlewood, J.E., Polya, G.: Inequalities. Cambridge University Press, Cambridge (1959)

    MATH  Google Scholar 

  12. Hong, K.S., Kim, C.W., Hong, K.T.: Boundary control of an axially moving belt system in a thin-metal production line. Int. J. Control, Automa. Systs. 1(2), 55–67 (2004)

  13. Kang, Y.H., Park, J.Y., Kim, J.A.: A memory type boundary stabilization for an Euler–Bernoulli beam under output feedback control. J. Korean. Math. Soc. 49(5), 947–964 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  14. Labidi, S., Tatar, N.-e.: Blow-up for the Euler-Bernoulli beam problem with a fractional boundary dissipation. Dyn. Syst. Appl. 17, 109–120 (2008)

  15. Lee, S.Y., Mote, C.D.: Wave characteristics and vibration control of translating beams by optimal boundary damping. J. Vib. Acoust 121(1), 18–25 (1999)

    Article  Google Scholar 

  16. Li, Y., Rahn, C.D.: Adaptive vibration isolation for axially moving beams. IEEE/ASME Trans. Mechatron. 5(4), 419–428 (2000)

    Article  Google Scholar 

  17. Park, J.Y., Kim, J.A.: Existence and uniform decay for Euler–Bernoulli beam equation with memory term. Maths. Methods Appl. Sci. 27(14), 1629–1640 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  18. Park, J.Y., Kim, J.A.: Global existence and stability for Euler–Bernoulli beam equation with memory condition at the boundary. J. Korean Math. Soc. 42(6), 1137–1152 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  19. Park, J.Y., Kang, Y.H., Kim, J.A.: Existence and exponential stability for an Euler–Bernoulli beam equation with memory and boundary output feedback control term. Acta. Appl. Math. 104, 287–301 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  20. Pata, V.: Exponential stability in linear viscoelasticity. Q. Appl. Math. LXIV(3), 499–513 (2006)

  21. Tabarrok, B., Leech, C.M., Kim, Y.I.: On the dynamics of an axially moving beam. J. Franklin Inst. 297(3), 201–220 (1974)

    Article  MATH  Google Scholar 

  22. Tatar, N.-e.: Polynomial stability without polynomial decay of the relaxation function. Math. Meth. Appl. Sci. 31(15), 1874–1886 (2008)

  23. Tatar, N.-e.: How far can relaxation functions be increasing in viscoelastic problems. Appl. Math. Lett. 22(3), 336–340 (2009)

  24. Tatar, N.-e.: Exponential decay for a viscoelastic problem with singular kernel. Zeit. Angew. Math. Phys. 60(4), 640–650 (2009)

  25. Tatar, N.-e.: On a large class of kernels yielding exponential stability in viscoelasticity. Appl. Math. Comp. 215(6), 2298–2306 (2009)

  26. Tatar, N.-e.: Arbitrary decays in linear viscoelasticity. J. Math. Phys. 52(1), 013502 (2011)

  27. Tatar, N.-e.: A new class of kernels leading to an arbitrary decay in viscoelasticity. Meditter. J. Math. 10, 213–226 (2013)

  28. Zhang, H.H., Matsuo, H., Morita, H., Yamakawa, H.: stability and stabilization of a deployable flexible structure. In: 37th IEEE Conference on Decision and Control, vol. 4, pp. 4541–4542 (1998 )

Download references

Acknowledgments

The second author is grateful for the financial support and the facilities provided by King Fahd University of Petroleum and Minerals.

Author information

Authors and Affiliations

  1. Faculté des Mathématiques, Université des Sciences et de la Technologie Houari Boumediene, BP 32, EL-Alia, 16111, Bab Ezzouar, Alger, Algeria

    Abdelkarim Kelleche

  2. Department of Mathematics and Statistics, King Fahd University of Petroleum and Minerals, Dhahran, 31261, Saudi Arabia

    Nasser-eddine Tatar

Authors
  1. Abdelkarim Kelleche
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nasser-eddine Tatar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Abdelkarim Kelleche.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kelleche, A., Tatar, Ne. Uniform Decay for Solutions of an Axially Moving Viscoelastic Beam. Appl Math Optim 75, 343–364 (2017). https://doi.org/10.1007/s00245-016-9334-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00245-016-9334-8

Keywords

Search

Navigation