1 Introduction

The heat transfer by natural convection is an attractive alternative to the forced convection, since there are neither fans nor blowers required. Hence, the noise emission and the electrical power consumption are usually lower and the system is simpler. Nevertheless, a major drawback of natural convection is the low heat transfer coefficient compared to forced convection. Therefore, the area for installation is higher or the heat transfer surface must be extended by fins or both. Common applications of such finned tube bundle heat exchangers are air conditioning and refrigerating systems, electronic cooling devices and thermal power plants. From the existing fin patterns the plain circular fin is the most common one, due to the simplicity and rigidity [1]. Since up to 85% of the thermal resistance occur on the gas side [2] new fin designs can contribute to improve these engineering parameters. Therefore, we devised two novel heat exchanger designs for improving the air-side convective heat transfer and enhancing the heat conduction in the solid part of the fin. These designs were additively manufactured by an SLM process and experimentally investigated in a chimney. In order to put the results into the context of the state of the art in this field, we will briefly discuss the latter in the following paragraphs.

One of the first heat transfer correlations for natural convection heat transfer from heated cylinders was developed by Churchill and Chu [3]. It was derived from numerous experimental data and is hence valid for a wide range of Rayleigh numbers and Prandtl numbers. Another heat transfer correlation based on Nusselt number and Rayleigh number for horizontal plain cylinders was proposed by Morgan [4]. Additionally, the natural convection of inclined plain tubes at angles between 0° and 90° was studied and it was found that the heat transfer reduces with inclination angle. Geometrical parameters such as fin diameter, fin spacing and temperature difference, were varied in the study of Kayansayan to understand their impact on the heat transfer [5]. It was found, that the beneficial ratio between fin spacing and fin diameter is between 0.25 and 0.5. Holographic interferometry was used by Herráez and Belda to analyse the temperature distribution and the heat transfer at a cylinder under natural convection [6]. The diameter as well as the Rayleigh number were changed between 10 mm and 30 mm as well as Ra = 2.2 · 103 and Ra = 1.6 · 105 respectively. Another experimental investigation, performed by Hahne et al., describes the influence of the fin height of a finned tube in the natural convection heat transfer [7]. For large fin heights the temperature distribution becomes more asymmetric and for short fins more symmetric. For single round fins the thermal performance was analytically analysed for different fin profiles by Mokheimer [8]. The fin efficiency was disclosed for circular fins with rectangular, triangular, concave parabolic and convex parabolic profile. 18 different finned tubes with fin diameters between 35 mm and 125 mm, fin spacings between 3.6 mm and 31.7 mm and a constant fin thickness of 1 mm were experimentally examined by Yildiz et al. [9]. The results indicate an optimum fin spacing at 8 mm for all fin diameters. A horizontal finned cylinder under natural convection was numerically and experimentally investigated for air cooling purpose by Yaghoubi and Mahdavi [10]. The flow developed from the downstream to the upstream part of the tube and the measured Nusselt numbers was described by an empirical correlation. The same authors studied the natural convection for air cooling by numerical and experimental methods. An approximately uniform temperature distribution on the fin as well as a laminar flow regime between the fins was observed. Furthermore, the Nusselt number was found slightly higher for cooled tubes compared to heated tubes. The influence of the rotation and the inclination of the longitudinal tube axis on the natural convection heat transfer of a plain tube was investigated by Elshazly et al. [11]. For these oval tubes an increase of the temperature with rotational angle was observed as well as an increase of heat transfer with rotational and inclination angle. A numerical simulation of a finned horizontal cylinder was performed by Dogan et al. [12]. The fin spacing, the fin diameter and the temperature difference were varied and the optimal heat dissipation found at s = 8.7 mm for fin diameters between 35 mm and 160 mm. The tube axis ratio of oval shaped tubes was changed by Ibrahim et al. between 1 : 4, 1 : 3, 1 : 2 and 1 : 1 (circular) [13]. As the eccentricity increases, the heat transfer and flow performance rises. The highest performance was achieved for an axis ratio of 1 : 4. Senapati et al. used a numerical method to study finned horizontal tubes with constant fin thickness, different tube diameters and various fin spacing [14]. Maximum heat transfer was reached for fin spacing between 5 mm and 6 mm at Rayleigh numbers between 5 and 108. Geometrical parameters such as fin length and fin width were studied for the melting of paraffin by Bondareva et al. [15]. The numerical analyses show that the fin width contributes to the formation of fluid circulations between the fins, which leads to reduced heat transfer. As the fin length increases the melting rate enhances significantly. Consequently, the time for the complete melting process decreased by 16 − 18% for an elongation of the fin from 0.1 to 0.3 and by 37 − 40% for an elongation to 0.6. In another examination the three dimensional fluid dynamic program FLUENT was applied to evaluate the natural convection heat transfer of single tubes with vertical plate fins [16]. The fin spacing as well as the tube diameter changed between 2 mm and 27.3 mm as well as between 10 mm and 20 mm respectively. The heat transfer coefficient increases for smaller tube diameter and greater fin spacing. The same authors studied elliptical finned tubes with different fin spacing [17]. It was found, that the fin efficiency of the elliptical fins is higher compared to annular circular fins as well as that the heat transfer coefficient increases with fin spacing until 18 mm. In a recent study, natural convection around a horizontal cylinder was simulated with computational fluid dynamics by Chen et al. [18]. The Zero-Equation-Turbulence model was used and two flow plumes were observed in the downstream area. Based on the numerical outcome a heat transfer correlation was proposed. Similar to the present study, selective laser melting was applied to manufacture two heat exchangers out of aluminium by Ho et al. [19]. Octet-grid-structures were used as porous fins on these air coolers and the heat transfer coefficient was found up to 2 times higher compared to conventional finned heat exchangers. The survey above shows, that natural convection heat transfer has been well studied for singles tubes. However, only little general knowledge exists for finned tube bundles under natural air convection.

One of the few studies dealing with the heat transfer from finned tube bundles under natural convection was performed by Katsuki et al. [20]. The heat transfer of the tube bundle increased with the tube pitch in vertical direction and stays constant as the tube pitch is greater than five times the tube diameter. Also, the heat transfer coefficient of the tube bundle was found 1.4 times higher than for the single tube. Kuntysh and Samorodov studied the effect of inclination angle on the natural convection around a finned tube bundle with a tube row number between one and five [21]. The heat transfer reduced with inclination angle due to higher blockage. In fact, the heat transfer rate was up to 67% lower for the 60° orientation compared to the horizontal orientation. In two of our own numerical simulations, the natural convection heat transfer was analysed by the commercial computational fluid dynamics code ANSYS CFX. Here, the influence of chimney height as well as fin parameters such as fin height, fin spacing and fin thickness on the heat transfer were analyzed [22]. An optimum heat transfer performance was found for a fin height of 17 mm, a fin spacing of 3 mm to 4 mm and a fin thickness of 1.5 mm. In the subsequent study the tube bundle parameters were changed, using the same method [23]. It was found, that oval tubes with an axis ratio of 1 : 2.1 in staggered configuration with minimum longitudinal and transversal tube pitches and tube row numbers between 2 and 3 achieve the greatest thermal performance. The longitudinal and transversal tube spacing of a finned tube bundle was experimental analysed by Novozhilova et al. [24]. It was found, that the Nusselt number increases with tube pitches and the measured data were represented by an empirical equation.

From the literature survey it was found, that the majority of the existing literature on heat transfer under natural convection deal with single tubes. Tube bundles were barely studied. To the knowledge of the authors there are no studies analysing novel fin designs in a natural convection scenario. Thus, the devised experimental study aims to contribute to a better understanding of the heat transfer from finned tube bundles in 2-row and 3-row configurations with novel heat exchanger designs. During the experiments the Rayleigh number, the tube row number and the fin design was changed, to find an optimum configuration.

2 Experimental apparatus

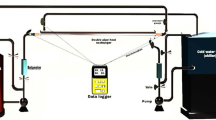
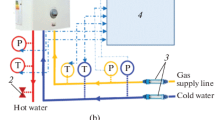
The investigated tube bundle heat exchangers were installed at the bottom of a 6.5 m long chimney. The distance between the chimney inlet and chimney outlet to the near surrounding was 2.5 m to minimize the effect of the environment. All experiments were performed in an experimental hall to avoid undesired influences, for example wind. The chimney was made out of PMMA and has an inner cross section of 0.27 × 0.172 m2 with ±0.5 mm manufacturing tolerances. Near to the chimney inlet the ambient temperature was measured by three type-K thermocouples. The outlet temperature was also measured by three thermocouples in the chimney. Furthermore, the humidity of the air flow was determined by a hygrometer and the pressure was measured at the particular day of the experiment by a pressure transducer. From the measured humidity, the pressure and the average of the six thermocouple readings the fluid properties were taken from the CoolProp library. A schematic of the vertical chimney and the position of the installed tube bundle heat exchanger is shown in Fig. 1.

Fig. 1
figure 1

Investigated chimney and tube bundle heat exchanger assembly

Full size image

We studied the heat transfer performance of 2-row and 3-row heat exchanger configurations in staggered arrangement. The finned oval tubes have a major tube axis of 30 mm and a minor tube axis of 15 mm. The finned tube bundle heat exchanger has a longitudinal tube pitch 68 mm and a transversal tube pitch of 53 mm. On all oval tubes fins with a height of 17 mm, a fin spacing of 5 mm and a fin thickness of 1 mm were installed. As a benchmark the conventional circular plain fin design (CPF) was used and compared to 2 novel fin designs, which are the circular integrated pin fin (CIPF) and the serrated integrated pin fin (SIPF) design. We investigated these heat exchanger designs for single tube heat exchanger in previous studies [25, 26]. The tube bundle heat exchangers consist out of several finned tubes, which are shown in Fig. 2. In the novel designs 16 pins with a diameter of 3 mm were integrated in the CIPF and SIPF fin surfaces. This material strengthening varies between neighbouring fins, to enhance the flow mixing. Hence, the minimum gap between some of the pinned fins was 4 mm. These pins improve the heat conduction from the fin base to the fin tip, due to a local increase of the fin cross section. Furthermore, the air-side turbulence and thus the air-side heat transfer on the fin surfaces is expected to enhance. In other studies advantages of serrated fins over plain fins was found [27]. For that reason, the SIPF combines the effect of integrated pins and serrated fins in one design. The heat exchangers were made out of stainless steel 316 L (thermal conductivity \( 16.2\frac{W}{mK} \)). Additive Selective Laser Melting (SLM) was used for the generation of the novel finned tube bundles by the Oerlikon Am Europe GmbH. These components were manufactured as a single component with a surface roughness of Rz = 21 μm and a solid connection between fins and tubes was achieved. Between the fins and the tubes of the conventional heat exchanger a fusing bonding was realized to allow a fair comparison to the novel finned tubes. Hence, the thermal resistance in the conjunction between the fins and the outer tube surface is small.

Fig. 2
figure 2

Investigated fin designs a) circular plain fin (CPF), b) circular integrated pin fin (CIPF) and c) serrated integrated pin fin (SIPF)

Full size image

The thermal power was supplied to the finned tubes by electrical heated rods, which were inserted into the tubes. For each tube row a direct current power source was connected to the heating rods and the remaining maximum deviation of current and voltage was ±0.014 A and ±0.3 V after calibration. As a result, the accuracy of the heat input was ±1.5% at maximum. In order to reduce the thermal resistance between the heating rods and the inner tube surface as well as to uniform the heat distribution, the gap was filled with copper powder. Along the outer tube surface 0.5 mm type-K thermocouples were fixed by cyanoacrylate adhesive. The thermocouple readings were used to calculate the average outer tube wall temperature. From our previous studies we found a homogenous temperature distribution along the tube axis using the applied experimental method [26, 28]. The installed thermocouples were guided to the heat exchangers by small feedthroughs at the chimney wall, which were tightened before each experiment. Furthermore, the thermocouples were calibrated and the remaining accuracy was ±0.3 K. In order to change the outer tube wall temperature, the heater power was adjusted by a controller to keep the average tube surface temperature constant. This temperature was increased from 40 ° C to 120 ° C in steps of 10 K. In between each step of temperature increase, a settling time of 30 min was foreseen to reach steady-state condition. Before we started the measurement campaign a settling time of about 1.5 h was kept. After reaching steady-state condition the measurements were tagged for 250 s with 1 sample per second. Next the 250 samples per sensor were averaged over time and used for the data processing. These collection and management of the data was done by a programmable logic controller (Phoenix-Contact™) and subsequently the data were transferred to an OPC server for visualization, data storage and data processing. The experimental campaigns were repeated up to 3 times, to ensure the reproducibility of the experimental setup. A deviation of Nusselt number, Rayleigh number and volumetric heat flux density was found to be below 4.62 % , 4.81% and 3.44%, respectively.

3 Method and data processing

3.1 Data analysis

The average air-side heat transfer coefficient for the natural convection was calculated from the measured data and the fluid properties as following:

$$ \mathrm{h}=\frac{\mathrm{Q}}{\left({\mathrm{A}}_{\mathrm{t}}+{\mathrm{A}}_{\mathrm{f}}\cdotp \upeta \right)\cdotp \Delta {\mathrm{T}}_{\mathrm{LM}}}, $$
(1)

where Q is the air-side heat transfer rate calculated from the heat input to the installed tube rows, At is the tube surface area of the installed tube rows, Af is the fin surface area of the installed tube rows and ∆TLM is the logarithmic mean temperature difference

$$ {\Delta \mathrm{T}}_{\mathrm{LM}}=\frac{\left({\mathrm{T}}_{\mathrm{in}}-{\mathrm{T}}_{\mathrm{t}}\right)-\left({\mathrm{T}}_{\mathrm{out}}-{\mathrm{T}}_{\mathrm{t}}\right)}{\ln \left(\frac{{\mathrm{T}}_{\mathrm{in}}-{\mathrm{T}}_{\mathrm{t}}}{{\mathrm{T}}_{\mathrm{out}}-{\mathrm{T}}_{\mathrm{t}}}\right)} $$
(2)

with the inlet temperature Tin, the outlet temperature Tout and the tube wall temperature Tt. Furthermore, heat input to the individual tube rows was measured separately to calculate the heat transfer coefficients of each tube row by

$$ {h}_i=\frac{Q_i}{\left({A}_{t_i}+{A}_{f_i}\cdotp \eta \right)\cdotp \varDelta {T}_{LM}},i=1,2,3 $$
(3)

where Qi is the air-side heat transfer rate calculated from the heat input of the corresponding tube row, \( {A}_{t_i} \) is the tube surface area of the corresponding tube row, \( {A}_{f_i} \) is the fin surface area of the corresponding tube row.

In order to determine the fin efficiency of the finned heat exchangers an iterative calculation was applied, similar to the approach introduced in the literature [29, 30]. Thus, from the approximation method of Shah and Sekulic´ [31] the two equations

$$ \upeta =\frac{\tanh \left(\mathrm{mH}\right)}{\mathrm{mH}} $$
(4)
$$ \mathrm{m}=\sqrt{\frac{2\mathrm{h}}{{\mathrm{k}}_{\mathrm{f}}{\mathrm{t}}_{\mathrm{f}}}} $$
(5)

were used. That means, an initial fin efficiency ηf in was determined. Then, Eqs. 1 or 3 was used to calculate the heat transfer coefficient. Next, Eqs. 4 and 5 were applied to determine the new fin efficiency ηf. The deviation between ηf and ηf in was calculated. The fin efficiency ηf was taken, when the deviation was less than 0.001%. When the deviation was more, the fin efficiency ηf was taken as the initial fin efficiency ηf in and the calculation processes was repeated until the deviation was below the deviation criterion. Eventually, Eqs. 1 or 3 was used to calculate the heat transfer coefficient of the tube bundle or of the individual tube row. The solution process is shown in Fig. 3.

Fig. 3
figure 3

Iterative scheme for the calculation of fin efficiency

Full size image

In the present study the equivalent of the circular diameter is used to define the hydraulic diameter, similar to the definition by Ibrahim et al. [13] and Elshazly et al. [11]

$$ {\mathrm{d}}_{\mathrm{h}}={\mathrm{d}}_{\mathrm{oval}}+\frac{2\ {\mathrm{h}}_{\mathrm{str}}}{\uppi}. $$
(6)

From this definition, the measured quantities and the fluid properties Nusselt number, Prandtl number and Rayleigh number are calculated by

$$ Nu=\frac{h\ {d}_h}{k_a} $$
(7)
$$ \mathit{\Pr}=\frac{\mu_a\ {c}_p}{k_a} $$
(8)
$$ Ra= Gr\ \mathit{\Pr}=\frac{g\ \beta\ {\rho}_a}{\mu_a\ {\alpha}_a}{\Delta \mathrm{T}}_{\mathrm{LM}}\ {d}_h^3. $$
(9)

In many applications the available space is limited and the heat transfer rate at a given volume is relevant. For that we assessed the compactness of a heat exchanger as given by Shah et al. [31] as the ratio of heat transfer surface to heat exchanger volume

$$ {\mathrm{C}}_{\mathrm{comp}}=\frac{\mathrm{A}}{\mathrm{L}{\mathrm{A}}_{\mathrm{fr}}}. $$
(10)

A is the heat transfer surface area and Afr the frontal area of the heat exchanger, L is the heat exchanger flow length and flow channel cross section (Fig. 2). Hence, the enveloped installation space of the heart exchanger is the product of frontal area and the flow length. From this definition the volumetric heat transfer density qvol is calculated in the present study, which represents the heat transfer per unit heat exchanger volume and per unit temperature difference

$$ {\mathrm{q}}_{\mathrm{vol}}=\frac{{\mathrm{C}}_{\mathrm{comp}}\mathrm{q}\ }{{\Delta \mathrm{T}}_{\mathrm{L}\mathrm{M}}}=\frac{\mathrm{A}}{\mathrm{L}{\mathrm{A}}_{\mathrm{fr}}}\frac{\mathrm{Q}}{\mathrm{A}{\Delta \mathrm{T}}_{\mathrm{L}\mathrm{M}}}=\frac{\mathrm{Q}}{\mathrm{L}{\mathrm{A}}_{\mathrm{fr}}{\Delta \mathrm{T}}_{\mathrm{L}\mathrm{M}}}=\frac{\mathrm{Q}}{{\mathrm{V}}_{\mathrm{HX}}{\Delta \mathrm{T}}_{\mathrm{L}\mathrm{M}}}. $$
(11)

3.2 Uncertainty analysis

The uncertainty of the primary measurements were considered to calculate the heat transfer quantities by the procedure described in the textbook of Taylor [32]. Hence, the following equation was applied:

$$ \Delta \mathrm{F}=\sqrt{\sum \limits_i{\left(\frac{\updelta \mathrm{F}}{{\updelta n}_i}\cdotp \Delta {n}_i\right)}^2}. $$
(12)

The target parameters F were calculated from the measured quantities ni. Furthermore, the manufacturing tolerances of the heat exchangers were taken into account. In Table 1 the maximum and minimum uncertainties of the individual target parameters (Ra, Nu, qvol) are listed and indicated as error bars in the diagrams.

Table 1 Uncertainties of the heat transfer and performance parameters
Full size table

4 Results and discussion

We studied the heat transfer characteristics of 2-row and 3-row finned tube bundle heat exchangers. Both configurations were equipped with plain circular fins (CPF), integrated pinned fins (CIPF) and serrated integrated pinned fins (SIPF). The average Nusselt number of the heat exchanger, the Nusselt number of the individual tube row and the volumetric heat flux density was used to describe the thermal performance.

4.1 Heat transfer characteristics of the novel fin designs

The influence of heat exchanger design and tube row number on average Nusselt number can be seen in Fig. 4 for different Rayleigh numbers. As the buoyancy induced flow velocity increases at higher tube wall temperature, the convective heat transfer enhances. Consequently, the Nusselt number improves for all designs and configurations at higher Rayleigh number. The Nusselt number is greater for the novel SIPF and lower for the CIPF compared to the conventional CPF for both tube configurations. The integrated pins in the fin surface induce additional turbulence and increase the heat conduction along the fin. Nevertheless, the integrated pins also result in a flow blockage and thus reduce the buoyancy induced flow velocity, which reduces the convective heat transfer. At the SIPF there is less surface area due to the serration and thus the flow blockage is less compared to the other designs. As a result the heat transfer is the highest. For the CIPF the flow blockage dominates over the enhancement due to the pins. In numbers, Nu of SIPF is on average 19.7% and 10.9% higher and Nu of the CIPF is 27.9% and 32.5% lower compared to the conventional CPF for the 3-row and 2-row configuration respectively.

Fig. 4
figure 4

Influence of fin design and tube row number on Nusselt number Nu for CPF, CIPF and SIPF at different Rayleigh numbers

Full size image

Furthermore, is can be seen, that the 2-row heat exchanger configuration gives greater Nusselt number compared to the 3-row heat exchanger for all fin designs, which was only observed for forced convection [33]. On the one hand, the air temperature rises further downstream and thus the temperature difference between heat exchanger surface and air reduces. Hence, the heat flux reduces as well. On the other hand, additional flow blockage occurs by the third tube row and the flow velocity as well as convective heat transfer reduces. The 2-row configuration reaches Nusselt number, which are on average 14.7% higher for the CPF, 10.0% higher for the CIPF and 5.8% higher for the SIPF compared to the 3-row configuration.

In Fig. 5 the convective heat transfer is shown for the individual tube rows and heat exchanger designs for the 3-row configuration at different Rayleigh number. Nu is highest for the first row and lowest for the third row. Especially the difference between the second and the third row is high. Hence, the differences of Nusselt number between the first row and second row as well as the second row and third row are on average 21.0% and 45.9% for CPF, 36.0% and 26.3% for CIPF as well as 2.1% and 42.5% for SIPF respectively.

Fig. 5
figure 5

Nusselt number for the individual tube rows and for the CPF, CIPF and SIPF of a 3-row heat exchanger at different Rayleigh numbers

Full size image

The Nusselt number of the individual rows are also calculated for the 2-row heat exchanger and illustrated in the Fig. 6 for different Rayleigh number and heat exchanger designs. It can be seen, that the two tube rows of the 2-row heat exchanger show similar heat transfer characteristics as the first tube rows of the 3-row heat exchanger. More in detail, Nu of the first row is higher compared to the second row by 22.8% for the CPF, 37.8% for the CIPF and 1.9% for the SIPF. An interesting aspect is that the SIPF gives small difference between the first tube rows. This may be, since the serrations allow a high flow mixing between the first rows. However, after the second row the air gets heated up and thus the heat transfer from the third row is low.

Fig. 6
figure 6

Nusselt number for the individual tube rows and for the CPF, CIPF and SIPF of a 2-row heat exchanger at different Rayleigh numbers

Full size image

4.2 Heat transfer performance of novel fin designs

In order to evaluate the heat transfer performance of the heat exchanger configurations, the heat flux per volume of heat exchanger at a certain temperature difference was applied as the volumetric heat flux density qvol, which was already used in our previous study [25, 34]. In the Fig. 7 the effect of heat exchanger design, tube row number and Rayleigh number on volumetric heat flux density are presented. It can be seen, that qvol rises with Ra similar to the Nusselt number. The effect of heat exchanger design on qvol reflects the findings on convective heat transfer. That is, the best compactness for the SIPF and the lowest for the CIPF. The average enhancement of qvol for the 2-row and 3-row heat exchanger configuration is for the SIPF 4.0% and 11.2% and the average reduction of the CIPF is 23.9% and 19.3% compared to the conventional design. Particularly the enhancement of SIPF is interesting, since the heat transfer surface is 30.7% lower compared to the conventional heat exchanger for the same enveloped volume of the heat exchanger. qvol is also higher for the 2-row configuration compared to the 3-row configuration, since the 2-row configuration requires less volume. Additionally, the contribution of the third row is small compared to the first and second row. In fact, the qvol of the 2-row configuration is on average 7.4% higher for the CPF, 2.7% higher for the CIPF and 0.2% higher for the SIPF compared to the 3-row configuration.

Fig. 7
figure 7

Influence of fin design and tube row number on volumetric heat flux density qvol for CPF, CIPF and SIPF at different Rayleigh numbers

Full size image

From the heat transfer analysis of heat exchangers with integrated pins, a beneficial performance of the SIPF was observed. Hence, we recommend this heat exchanger design for natural convection applications. Eventually, the heat exchanger configuration with SIPF requires 30.7% and 6.9% less surface area and volume compared to the conventional CPF design. Thus, the material consumption and cost for manufacturing as well as the weight of the heat exchanger can be lowered, while the heat transfer is higher. If the chimney height rises or the temperature differences increase, the buoyancy induced velocity increases and the CIPF may become more beneficial. Nevertheless, in the present study the CIPF underperforms the conventional plain fin design, due to the high flow blockage. Moreover, for all heat exchanger designs the 2-row configuration gives higher Nusselt number and volumetric heat flux density compared to the 3-row configuration. As a result we recommend the 2-row heat exchanger configuration with SIPF. The data of the present study are listed in Table 2 for the 3-row and the 2-row heat exchanger.

Table 2 Measured heat transfer parameters for the 3-row and 2-row configuration
Full size table

4.3 Heat transfer correlations

To allow the usage of the presented novel heat exchanger design, we developed an empirical heat transfer correlation for the Nusselt number as a function of the Rayleigh number, Prandtl number, the heat exchanger design and the tube row number as following:

$$ Nu={K}_1\cdotp {Ra}^{K_2}\cdotp {\mathit{\Pr}}^{0,33}\cdotp {K}_3\cdotp N. $$
(13)

In this correlation the constants depend on the described heat exchanger design. They are listed in Table 3 and the correlation is valid for Rayleigh numbers between 25,000 < Ra < 120,000 and tube row numbers of 2 and 3. K3 = 0.5 for the 2-row configuration and K3 = 0.302 for the 3-row configuration.

Table 3 Constants used in Eq. (13), depending on the fin design
Full size table

The correlation is compared with the experimental data in Fig. 8. A maximum and average deviation of 5.4% and 2.0% between the correlation and the experimental data was calculated and R2 = 0.9941. The proposed correlation may be of use for the design and the operation of finned tube bundle heat exchanger with novel designs under natural convection.

Fig. 8
figure 8

Comparison of the experimentally determined Nusselt number and the prediction by the correlation

Full size image

5 Conclusions

In the present study the natural convection heat transfer from a finned tube bundle heat exchanger was experimental analysed. Novel heat exchanger designs with integrated pin fins were additively manufactured in 2-row and 3-row configuration to improve the conduction heat transfer within the fin and the convective heat transfer along the fin simultaneously. The major findings of this study are:

  1. (1)

    The Nusselt number is greater for the SIPF and lower for the CIPF compared to the CPF. The reason for this is that, the SIPF achieves higher convection while having low flow blockage.

  2. (2)

    2-row heat exchangers achieve higher convective heat transfer than 3-row heat exchangers, due to higher flow blockage as well as reduced flow velocity and convective heat transfer of the 3-row heat exchangers.

  3. (3)

    The first tube rows give highest Nusselt number and the last tube rows give lowest Nusselt number, since the flow mixing is high in the first tube rows and the air is more heated at the last tube rows.

  4. (4)

    The SIPF reaches greatest and the CIPF lowest volumetric heat flux density. This can be explained by the difference in convective heat transfer of the finned tube bundle designs.

  5. (5)

    The experimental outcome was used to develop a heat transfer correlation for engineering applications.

The experimental data of the present study can be found here https://doi.org/10.14278/rodare.320.