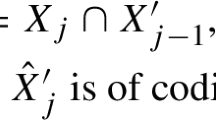Cracked polytopes and Fano toric complete intersections

Abstract

We introduce the notion of cracked polytope, and – making use of joint work with Coates and Kasprzyk—construct the associated toric variety X as a subvariety of a smooth toric variety Y under certain conditions. Restricting to the case in which this subvariety is a complete intersection, we present a sufficient condition for a smoothing of X to exist inside Y. We exhibit a relative anti-canonical divisor for this smoothing of X, and show that the general member is simple normal crossings.

1 Introduction

We introduce a class of polytopes which we call cracked. Given a complete fan $\Sigma$ (a shape) these are polytopes whose intersection with the maximal cones of $\Sigma$ forms a set of unimodular polytopes. We propose that this class of polytopes is particularly well adapted to the study of toric degenerations of Fano varieties.

Our basis for this claim stems from our use of the method Laurent inversion—developed jointly with Coates and Kasprzyk [10]—to embed the toric variety X associated with a given cracked polytope into an ambient toric variety Y, such that X degenerates to a union of toric strata of Y. Indeed the definition of cracked is a natural necessary condition for the ambient variety Y to be smooth, and we give precise sufficient conditions in Theorem 1.1.

We aim to apply these ideas to systematically construct Fano varieties. Indeed, every Fano threefold with a very ample anti-canonical divisor can be constructed from a cracked polytope via an explicit deformation of an embedding obtained via Laurent inversion. This is the subject of work in progress [23], drawing on the constructions of Coates–Corti–Galkin–Kasprzyk [7], and the work on toric degenerations of Ilten–Christophersen [4, 5] and Galkin [13]. One important practical point is that one only requires a small list of shapes to achieve this. Given that the class of cracked polytopes with a given shape is small, one can classify those of a given shape, use the techniques explained below to construct an embedded deformation of the corresponding toric variety and thereby systematically recover every Fano threefold (with $-K$ very ample) without advance knowledge of the classification. It may be that every Fano fourfold with–K very ample can be constructed using a similarly restricted list of shapes.

In Sect. 3 we give a self-contained account of the procedure Laurent inversion which takes as input a decoration of P called a scaffolding, see Definition 3.1, and returns an embedding of $X_P$ into a toric variety Y. The content of Sect. 3 first appeared in the joint work [10]. Our first main result is proved in Sect. 4, which provides a characterisation of when Y is smooth in a neighbourhood of the image of $X_P$. Note that given a fan $\Sigma$ we let $\bar{\Sigma }$ denote the quotient of $\Sigma$ by its minimal cone.

Theorem 1.1

Fix a polytope $P \subset M_{\mathbb {R}}$, and a rational fan $\Sigma$ in $M_{\mathbb {R}}$ such that the toric variety $Z:= {{\,\mathrm{TV}\,}}(\bar{\Sigma })$ is smooth and projective. Given a scaffolding S of P with shape Z, we have that the target of the corresponding embedding is smooth in a neighbourhood of the image of $X_P$ if and only if P is cracked along $\Sigma$ and S is full—see Definitions 2.1 and 4.1.

If Z is a product of projective spaces it follows from Proposition 5.1 that $X_P$ is a complete intersection in $Y_S$. If the line bundles defining this complete intersection are basepoint free, $X_P$ will smooth inside $Y_S$ by Bertini’s theorem. We provide a weaker, though related, criterion for the smoothability of $X_P$ inside $Y_S$, which we call positivity of S: a condition on the codimension one slabs of the union of toric varieties to which $X_P$ degenerates. This criterion has practical and theoretical advantages over the naive one. For example – in the context of the Gross–Siebert program [15, 16]—it is related to the notion of positivity of the log structure on the central fibre of a toric degeneration, as defined in [15]. We expect a precise understanding of this connection to lead to a proof of Conjecture 5.11. We also explain in future work that this condition is closely related to the condition required to smooth a cracked polytope as an integral affine manifold. In practice it also reduces the problem of computing basepoint loci on $Y_S$ to the problem of computing their restriction to $(\dim X_P{-} 1)$ dimensional toric strata of $Y_S$.

Theorem 1.2

Fix a fan $\Sigma$ such that $Z:= {{\,\mathrm{TV}\,}}(\bar{\Sigma })$ is a product of projective spaces, and fix a polytope P such that $P^\circ$ is cracked along $\Sigma$. Given a full scaffolding S of P with shape Z, the toric variety $X_P$ is the intersection of r Cartier divisors corresponding to line bundles $L_1,\ldots , L_r \in {{\,\mathrm{Pic}\,}}Y_S$. If S is positive we have that:

• (i) The vanishing locus of a general section of $\bigoplus _{i \in [r]}{L_i}$ is a smooth variety.

• (ii) There is a divisor $D_S$ on $Y_S$ such that the restriction of $D_S$ to the vanishing locus of a general section of $\bigoplus _{i \in [r]}{L_i}$ is simple normal crossings and anti-canonical.

While we do not attempt to classify cracked polytopes in this article, we study the special case in which (after removing torus factors) $Z \cong {\mathbb {P}}^1$ in detail in [9]. In particular, among other results, we will give a classification when $\dim P \in \{3,4\}$.

The current work is related to the broad project of Coates, Corti, Galkin, Golyshev, Kasprzyk, and others to construct and classify Fano varieties via mirror symmetry [1, 2, 6, 7]. In particular, given a scaffolding S defining a complete intersection, there is a Laurent polynomial$f_S$, defined in [10]. If $X_P$ is cut out by a collection of nef line bundles, the Quantum Lefschetz Hyperplane Theorem of Coates–Givental [8] implies that $f_S$ is mirror to the smoothing of $X_P$ in the sense defined in [6]. Moreover positivity of S implies that $f_S$ admits a certain collection of mutations—that is, $f_S$ remains a regular function on a torus under certain birational transformations—see [2, 6, 14].

We also remark on a connection with polyhedral combinatorics. Cracked polytopes are reflexive polytopes made up of a number of hollow polytopes, that is, of polytopes without interior points. These are themselves objects of interest and recent study, see for example [3, 21]. It would be interesting to investigate whether these works provide tools to allow us to classify cracked polytopes.

Conventions. Throughout this article $N \cong {\mathbb {Z}}^n$ will refer to an n-dimensional lattice, and $M:= \hom (N,{\mathbb {Z}})$ will refer to the dual lattice. Given a ring R we write $N_R:= N \otimes _{\mathbb {Z}}R$ and $M_R:= M \otimes _{\mathbb {Z}}R$. For brevity we let [k] denote the set $\{1,\ldots ,k\}$ for each $k \in {\mathbb {Z}}_{\ge 1}$. We work over an algebraically closed field $\mathbb {k}$ of characteristic zero.

2 Cracked polytopes

In this section we introduce the notion of cracked polytope, which will form our main object of study, and, in the Fano setting, characterize its dual polytope. We will assume basic ideas and results from toric geometry—see [11, 12]—throughout.

Definition 2.1

Fix a convex polyhedron $P \subset M_{\mathbb {R}}$ containing the origin in its interior, and a unimodular fan $\Sigma$. We say P is cracked along$\Sigma$ if every tangent cone of $P \cap C$ is unimodular for every maximal cone C of $\Sigma$.

Example 2.2

Figure 1 shows an example of a polygon P cracked along the fan of ${\mathbb {P}}^2$. The toric variety defined by the normal fan of P is ${\mathbb {P}}^2/\mu _3$. This surface is isomorphic to the singular cubic surface $\{x_1x_2x_3 = x_0^3\} \subset {\mathbb {P}}^3$, where $x_i$, $i \in \{0,\ldots ,3\}$ are homogeneous co-ordinates on ${\mathbb {P}}^3$. Clearly, if we replace this binomial with a general cubic, the resulting variety is smooth. Here we see P breaking into polytopes $P_i$, $i \in [3]$, which we will later identify with the toric divisors $\{x_i = 0\}$ for $i \in [3]$.

Fig. 1

Cracking a polygon

Example 2.3

We present two three-dimensional examples of cracked polytopes in Fig. 2. The left-hand example uses the simplest non-trivial fan, consisting of two maximal cones meeting along a hyperplane. The normal fan of the toric variety shown is isomorphic to the blow-up in a smooth point of a quadric in ${\mathbb {P}}^4$ which contains a line of singularities. This variety admits an embedded smoothing in ${\mathbb {P}}^4$ blown up at a (reduced) point.

The polytope P shown in the right-hand example is cracked along the fan of ${\mathbb {P}}^1\times {\mathbb {P}}^1 \times {\mathbb {P}}^1$. The normal fan of P in this case defines a toric variety isomorphic to

$$\begin{aligned} V(x_1y_1 - x_0y_0, x_2y_2 - x_0y_0, x_3y_3 - x_0y_0) \subset {\mathbb {P}}^3\times {\mathbb {P}}^3 \end{aligned}$$

where $x_i$ and $y_i$ are homogeneous co-ordinates on the respective ${\mathbb {P}}^3$ factors. $X_P$ contains 12 ordinary double point singularities. These are smoothed by perturbing the equations defining $X_P$ in ${\mathbb {P}}^3 \times {\mathbb {P}}^3$, which then define the vanishing locus of a general section of $\bigoplus _{i \in [3]}\mathcal {O}_{{\mathbb {P}}^3\times {\mathbb {P}}^3}(2,2)$.

Fig. 2

Examples of cracked polytopes

Note that we do not assume the origin is the minimal cone of $\Sigma$ in Definition 2.1. We let $\bar{M}$ denote the quotient of M by the minimal cone of $\Sigma$.

Remark 2.4

Although we provide a general definition, this article is concerned solely with the case that $\bar{\Sigma }$ defines a projective toric variety, and P is a polytope containing the origin in its interior.

We study cracked polyhedra which are the image of the moment map of an anti-canonically polarised toric Fano variety. Recall that an integral polytope $P \subset N_{\mathbb {R}}$ is called Fano if it contains the origin in its interior, and every vertex of P is primitive.

In general the polar polytope $P^\circ \subset M_{\mathbb {R}}$ of a Fano polytope P is not integral, which is true in the special case that P is reflexive. Given a Fano polytope P its spanning fan is the fan whose cones are given by the cones over faces of P, and we denote the toric variety determined by the spanning fan of P by $X_P$. We also recall that there is an inclusion reversing map between the faces of P and $P^\circ$. Let $F^\star$ denote the face dual to the face F of P or $P^\circ$.

Proposition 2.5

Let P be a Fano polytope cracked along a unimodular and complete fan $\Sigma$, then P is reflexive. Hence there are only finitely many polytopes of a fixed dimension cracked along some complete fan.

Proof

We show that, for every vertex $v \in {\text {verts}}\left( {P^\circ }\right)$, the vertices of the facet $v^\star$ of P lie in a hyperplane of $\{ v \in N_{\mathbb {R}}: \langle u,v\rangle = 1\}$ for some $u \in M$. Let C be the minimal cone of $\Sigma$ containing v in its relative interior, and let $k := \dim C$. Let $C_v$ denote the tangent cone of $P^\circ$ at v, and let $\{b_1,\ldots , b_k\}$ be the minimal generating set of the unimodular cone $C_v\cap \langle C\rangle$.

Every facet F of $P^\circ$ containing v is contained in an affine hyperplane spanned by $n-1$ of the vectors $\{b_1,\ldots , b_n\}$, the basis of the tangent cone to $C_v \cap \langle B \rangle$ at v for some maximal cone B of $\Sigma$. Moreover this collection cannot contain $\{b_1,\ldots , b_k\}$, as the affine subspace spanned by these k vectors contains the origin. Thus if $F^\star = \{w\}$, $w = b_j^\star$ for some $j \in [k]$ and $\langle \sum _{i \in [k]}{b_i}, w\rangle = 1$. Since $\sum _{i \in [k]}{b_i}$ is defined independently of F and B, $v^\star \subset \langle \sum _{i \in [k]}{b_i}, -\rangle = 1$. $\square$

Let $P \subset N_{\mathbb {R}}$ be a reflexive polytope such that $P^\circ$ is cracked along a fan $\Sigma$ in $M_{\mathbb {R}}$; assume moreover that $\Sigma$ defines a projective toric variety Z. We now characterize the facets of P.

Definition 2.6

Recall the Cayley sum$P_1 \star \cdots \star P_r$ of polytopes $P_i \subset N_{\mathbb {R}}$ for $i \in [r]$ is the convex hull of the union of the polytopes $P_i + e_i$ in $N_{\mathbb {R}}\oplus {\mathbb {R}}^r$ for $i \in [r]$.

Given a fan $\Sigma$ in $M_{\mathbb {R}}$ defining a projective toric variety Z, and C a cone of $\Sigma$, let $Z_C$ denote the subvariety of the toric boundary corresponding to C under the orbit-cone correspondence.

Definition 2.7

Let $P \subset N_{\mathbb {R}}$ be a Fano polytope and $\Sigma$ a fan in $M_{\mathbb {R}}$. We say P has facets of Cayley type if every facet F of P is affine linearly isomorphic to the Cayley sum of polyhedra associated to nef divisors of $Z_C$, where C is the minimal cone of $\Sigma$ containing the vertex $F^\star$ of $P^\circ$. Moreover we insist that this isomorphism identifies ${{\,\mathrm{Ann}\,}}\langle C \rangle \subset N$ with the character lattice of $Z_C$.

Proposition 2.8

Fix a reflexive polytope P such that $P^\circ$ is cracked along a fan $\Sigma$. Assuming that $Z:= {{\,\mathrm{TV}\,}}(\bar{\Sigma })$ is a smooth projective toric variety, P has facets of Cayley type.

Proof

Let $C_v$ denote the tangent cone to $P^\circ$ at v. Let $\Sigma _v$ be the fan induced by $C_v$ in the quotient space $M_{\mathbb {R}}/\langle v\rangle$. Let C be the minimal cone of $\Sigma$ containing v, and let $\{b_1,\ldots , b_k\}$ denote the minimal generating set of $C_v \cap \langle C\rangle$, where $k:= \dim C$.

We construct a fan $\widetilde{\Sigma }_v$ in $M_{\mathbb {R}}/\langle v \rangle$ refining $\Sigma _v$. Fix a maximal cone $\sigma \ni v$ of $\Sigma$ and let $\{b_1,\ldots ,b_n\}$ be the extension of $\{b_1,\ldots , b_k\}$ to the minimal generating set of the tangent cone $\sigma _v$ to $\sigma$ at v. The cone $\langle b_i: i \in [n], i\ne j \rangle$ projects to a full-dimensional unimodular cone in $M_{\mathbb {R}}/\langle v \rangle$ for any $j \in [k]$. We define $\widetilde{\Sigma }_v$ to be the complete fan formed by these maximal cones for all $\sigma \ni v$.

As every maximal cone of $\widetilde{\Sigma }_v$ contains $k-1$ vectors $b_i$ for $i \in [k]$, the toric variety $X_v$ defined by $\widetilde{\Sigma }_v$ admits a projection given by the quotient $M_{\mathbb {R}}/\langle v \rangle \rightarrow M_{\mathbb {R}}/\langle C \rangle$ to the toric variety $Z_C$. Since, by the proof of Proposition 2.5, the anti-canonical (Gorenstein) direction for ${{\,\mathrm{cone}\,}}(v^\star )$ is $u:= \sum _{i \in [k]}{b_i}$, u is in the kernel of the map $M_{\mathbb {R}}\rightarrow M_{\mathbb {R}}/\langle v \rangle$. Thus the fibres of the projection $X_v \rightarrow Z_C$ are isomorphic to ${\mathbb {P}}^{k-1}$.

We write $C_v$ as the region above a convex PL-function $\theta :M_{\mathbb {R}}/\langle v\rangle \rightarrow {\mathbb {R}}$. First note that, by reflexivity of P, fixing a vertex w of the facet $v^\star$ determines a splitting of N into the sublattice annihilating $v \in M$, and the direction generated by w. Identifying $M_{\mathbb {R}}/\langle v \rangle$ with ${{\,\mathrm{Ann}\,}}(w)$ we identify $M_{\mathbb {R}}$ with $M_{\mathbb {R}}/\langle v \rangle \oplus \langle v \rangle$, and hence identify $\partial C_v$ with a graph of a function $\theta$ on $M_{\mathbb {R}}/\langle v \rangle$. Note that $v^\star$ is the polyhedron of sections of the corresponding divisor on the toric variety $X_v$ associated to $\widetilde{\Sigma }_v$.

Let $\bar{b}_i$ be the images of $b_i$ in $M_{\mathbb {R}}/\langle v \rangle$ for $i \in [k]$. Recall that each maximal cone of $\widetilde{\Sigma }_v$ contains ${k-1}$ of the vectors $\bar{b}_i$, for $i \in [k]$. Therefore the function $\theta$ vanishes on all but a single ray of the k rays in the subspace $\langle C\rangle /\langle v\rangle \subset M_{\mathbb {R}}/\langle v \rangle$, and evaluates to 1 on the remaining ray by unimodularity. Relabelling the elements $b_i$ we may assume that $\langle u, b_i\rangle = 0$ for all $i \in [k-1]$. Since $\theta (\bar{b}_k) = 1$, $v^\star$ (regarded as a polytope in ${{\,\mathrm{Ann}\,}}(v)$) is contained in the column

$$\begin{aligned} \bigcap _{i \in [k-1]} \{u: u \in {{\,\mathrm{Ann}\,}}(v), \langle \bar{b}_i,u\rangle \ge 0\} \cap \{u: u \in {{\,\mathrm{Ann}\,}}(v), \langle \bar{b}_k, u \rangle \ge -1\}. \end{aligned}$$

Thus $v^\star$ projects to the standard simplex in the vector space dual to $\langle C\rangle /\langle v\rangle$ and hence is a Cayley sum.

Recall that there is a surjection from the set of maximal cones of $\widetilde{\Sigma }_v$ to the vertices of $v^\star$. Fix a maximal cone of $\widetilde{\Sigma }_v$ and assume, without loss of generality, that it contains the vectors $\{\bar{b}_1,\ldots , \bar{b}_{k-1}\}$. The vertex of $v^\star$ dual to this maximal cone is contained in the subspace annihilating every $\bar{b}_i$ for $i \in [k-1]$. The face of $v^\star$ contained in this subspace, is nothing other than the polyhedron of sections of the divisor on $Z_C$ obtained from the convex piecewise linear function induced by $\theta$ on the quotient fan $\widetilde{\Sigma }_v/\langle \bar{b}_1,\ldots ,\bar{b}_{k-1}\rangle$. This is a nef divisor on $Z_C$ as $\theta$ is a convex function on the fan $\widetilde{\Sigma }_v$. $\square$

Remark 2.9

Note that the converse to Proposition 2.8 is not true. For example, any smooth lattice polytope $P \subset N_{\mathbb {R}}$ has Cayley facets for the fan subdividing $M_{\mathbb {R}}$ into two half-spaces meeting along the annihilator of any vector $u \in N$ such that $v \notin {{\,\mathrm{Ann}\,}}(u)$ for all $v \in {\text {verts}}\left( {P^\circ }\right)$. However slicing $P^\circ$ by the annihilator of u will not produce a pair of polytopes with unimodular tangent cones in general.

Fix a Fano polytope P such that $P^\circ$ is cracked along a fan $\Sigma$. Since facets of P are of Cayley type, there is a projection $\pi _F :F \rightarrow \Delta _{k-1}$ where k is the dimension of the minimal cone of $\Sigma$ containing the dual vertex to the facet F, and $\Delta _l$ is the standard simplex of dimension l.

Definition 2.10

Given a reflexive polytope P such that $P^\circ$ is cracked along a fan $\Sigma$ we say a face E is vertical if, for any facet F containing E, $\pi _F(E)$ is a vertex of $\Delta _{k-1}$,

3 Laurent inversion

In this section we recall the method, Laurent inversion, developed in [10]. Throughout this section we fix a lattice $N \cong {\mathbb {Z}}^n$, a splitting of $N = \bar{N} \oplus N_U$ and a Fano polytope $P \subset N_{\mathbb {R}}$. Given these data we can define the notion of scaffolding on P, see [10, Definition 3.1].

Definition 3.1

Fix a smooth projective toric variety Z with character lattice $\bar{N}$. A scaffolding of P is a set of pairs $(D,\chi )$ where D is a nef divisor on Z and $\chi$ is an element of $N_U$, such that

$$\begin{aligned} P = {\text {conv}}\left( {P_D + \chi \, \Big | \, (D,\chi ) \in S}\right) . \end{aligned}$$

We refer to Z as the shape of the scaffolding, and elements $(D,\chi ) \in S$ as struts. We also assume that for every vertex of P, there is a unique $s = (D,\chi )$ such that $v \in P_D+\chi$.

Note that the assumption that vertices meet a unique polytope $P_D+\chi$ did not appear in the Definition given in [10]. This is an innocuous technical condition which we make use of to prove Theorem 1.1.

We let $\ell$ denote the rank of the free abelian group ${{\,\mathrm{Div}\,}}_{T_{\bar{M}}}Z$. Following [10] we show that a scaffolding yields a torus invariant embedding of $X_P$ into an ambient toric variety $Y_S$.

Definition 3.2

[10, Definition A.1] Given a scaffolding S of P we define a toric variety $Y_S$, associated to the normal fan $\Sigma _S$ of the polytope $Q_S \subset \widetilde{M}_{\mathbb {R}}:= ({{\,\mathrm{Div}\,}}_{T_{\bar{M}}}Z \oplus M_U)\otimes _{\mathbb {Z}}{\mathbb {R}}$, itself defined by the following inequalities:

$$\begin{aligned} \begin{array}{l@{\quad }l} \big \langle (-D,\chi ), - \big \rangle \ge -1 &{} \text {for all }(D,\chi ) \in S;\\ \big \langle (e_i,0), - \big \rangle \ge 0 &{} \text {for }i \in [\ell ], \end{array} \end{aligned}$$

where $e_i$ denotes the standard basis of ${{\,\mathrm{Div}\,}}_{T_{\bar{M}}}Z \cong {\mathbb {Z}}^\ell$.

Let $E_i$ denote the divisor of Z corresponding to the lattice vector $e_i$ and define $\rho _s:= (-D,\chi )$ for each $s = (D,\chi ) \in S$. We define a map of lattices

where $\rho$ is the ray map of the fan $\bar{\Sigma }$ determined by Z.

Theorem 3.3

[10, Theorem 5.5] A scaffolding S of a polytope P determines a toric variety $Y_S$ and an embedding $X_P \rightarrow Y_S$. This map is induced by the map $\theta$ on the corresponding lattices of one-parameter subgroups.

Let ${\text {verts}}\left( {S}\right)$ denote the set of torus fixed points of Z, and, for each $u \in {\text {verts}}\left( {S}\right)$, let $C_u$ denote the intersection of the maximal cone of $\Sigma$ corresponding to u with $P^\circ$. Observe that, given a nef divisor D on Z, there is a canonical surjection ${\text {verts}}\left( {S}\right) \rightarrow {\text {verts}}\left( {P_{D}}\right)$. We denote this map $v \mapsto v^D$. Each element $u \in {\text {verts}}\left( {S}\right)$ defines a function $u :S \rightarrow N$, defined by setting $u\left( (D,\chi )\right) = u^D + \chi$.

Definition 3.4

Let $\iota$ be the inverse map to the restriction to $\Gamma \oplus N_U$ of the canonical projection $\widetilde{M}_{\mathbb {R}}\rightarrow M_{\mathbb {R}}$, where $\Gamma$ is the union of $(n - \dim N_U)$-dimensional faces of the standard coordinate cone in ${{\,\mathrm{Div}\,}}_{T_{\bar{M}}}(Z)^\star$ which project onto maximal dimensional cones of $\bar{\Sigma }$.

Let $\iota _u :M_{\mathbb {R}}\rightarrow \widetilde{M}_{\mathbb {R}}$ be the linear extension of the map $\iota |_{C_u}:C_u \rightarrow \widetilde{M}_{\mathbb {R}}$ for each $u \in {\text {verts}}\left( {S}\right)$.

Lemma 3.5

Given an element $s \in S$ and $u \in {\text {verts}}\left( {S}\right)$, we have that

$$\begin{aligned} \iota _u^\star \rho _s = u(s). \end{aligned}$$

Proof

The ray generators of the maximal cone in $M_{\mathbb {R}}$ corresponding to u form a basis $\{\bar{e}_i : i \in [\dim (\bar{M})]\}$ of $\bar{M}$. Moreover the vectors $\iota _u(\bar{e}_i)$ are standard basis vectors $e^\star _i$ in ${{\,\mathrm{Div}\,}}_{T_{\bar{M}}}(Z)^\star \subseteq \widetilde{M}_{\mathbb {R}}$. Thus we have that

$$\begin{aligned} \langle \iota _u^\star \rho _s, \bar{e}_i\rangle = \langle \rho _s, e^\star _i\rangle . \end{aligned}$$

Writing $s = (D,\chi )$, one of the defining inequalities of $P_D$ is

$$\begin{aligned} \langle -,\bar{e}_i\rangle \ge -\langle \rho _s, e^\star _i\rangle . \end{aligned}$$

That is, writing the projection of $\iota _u^\star \rho _s$ to $\bar{N}$ in co-ordinates determined by the basis $\bar{e}^\star _i$, and recalling that $\rho _s = (-D,\chi )$, we have that these co-ordinates are identical to those of u(s). Note that since $\iota _u$ acts as the identity on $M_U$ the result follows. $\square$

Proposition 3.6

[10, Proposition A.9] The polytope $\iota (C_u)$ is a face of $Q_S$ for each $u \in {\text {verts}}\left( {S}\right)$.

Proof

The polytope $\iota (C_u)$ is clearly contained in the boundary of the standard positive cone. Given any $s \in S$ and $p \in C_u$, $\langle \rho _s,\iota (p)\rangle = \langle u(s), p\rangle \ge -1$ by Lemma 3.5. Thus $\iota (C_u)$ is contained in a face of $Q_S$; the reverse inclusion follows similarly. $\square$

Lemma 3.7

Given a vertex $v \in {\text {verts}}\left( {P^\circ }\right)$, the tangent cone of $Q_S$ at $\iota (v)$ is defined by the following inequalities:

$$\begin{aligned} \begin{array}{ll} \big \langle \rho _s, - \big \rangle \ge -1 &{} s=(D,\chi ) \in S\text { such that }(P_D+\chi ) \cap v^\star \ne \varnothing ;\\ \big \langle (e_i,0), - \big \rangle \ge 0 &{} u \notin E_i\text { for some }u\text { such that }v \in C_u, \end{array} \end{aligned}$$

Proof

By Lemma 3.5$\langle \rho _s, \iota (v)\rangle = \langle u(s),v \rangle$ for any $u \in {\text {verts}}\left( {S}\right)$ such that $v \in C_u$. This is equal to $-1$ if and only if $u(s) \in v^\star$. The second set inequalities follow as $\iota (v)$ is in the span of those $e^\star _i$ corresponding to rays of $\bar{C}$, where C is the minimal cone of $\Sigma$ containing v and $\bar{C}$ is the projection of C to $\bar{M}$. $\square$

Proof of Theorem 3.3

Given a vertex $v \in {\text {verts}}\left( {P^\circ }\right)$, let $C_v$ denote the tangent cone of $P^\circ$ at v, and let $\widetilde{C}_v$ denote the tangent cone of $Q_S$ at $\iota (v)$. We prove that $\theta ^\star (\widetilde{C}_v) = C_v$. By Proposition 3.6 we have that $C_v \subseteq \theta ^\star (\widetilde{C}_v)$. Fix a point $p \in \widetilde{C}_v$ and a vertex $w \in {\text {verts}}\left( {v^\star }\right)$. We have that $w = \iota _u^\star \rho _s$ for some $s \in S$ and $u \in {\text {verts}}\left( {S}\right)$. Now $\langle \theta (w),p \rangle = \langle \rho _s,p \rangle + \langle \theta (w)-\rho _s,p \rangle$. Note that $\langle \rho _s,p \rangle \ge -1$ by Lemma 3.7. After projecting $\widetilde{N}\rightarrow {{\,\mathrm{Div}\,}}_{T_{\bar{M}}}Z$, the polyhedron of sections of the divisor $\theta (w)-\rho _s$ is the translate of $P_D$ defined by taking the vertex w to the origin. Thus, writing out $\theta (w)-\rho _s$ in the basis $e_i$, $i \in [\ell ]$, the components corresponding to divisors $E_i$ containing any u such that $u(s) = w$ vanish; while all others have non-negative coefficient. Thus $\langle \theta (w)-\rho _s,p \rangle \ge 0$, and $\langle w,\theta ^\star (p)\rangle \ge -1$, as required. Finally, we need to show that the map $\theta ^\star$ defines a surjection of semigroups. This follows from Proposition 3.6: as Z is smooth each $\iota _u$ is an integral splitting of $\theta ^\star$. $\square$

We describe the construction of $Y_S$ and the embedding $X_P \hookrightarrow Y_S$ in a simple example.

Example 3.8

Consider the polygon P shown in Fig. 3. Fixing the shape variety ${\mathbb {P}}^2$, Fig. 3 shows a scaffolding of P with two struts. The dual polytope is shown on the right-hand side of Fig. 3, where it is easily seen that this polygon is cracked along the fan of ${\mathbb {P}}^2$. Note that in this example $\overline{N} = N$ and $N_U = \{0\}$.

Fig. 3

Scaffolding a polygon

The polytope $Q_S \subset {\mathbb {R}}^3$ is defined by the inequalities $\langle e_i, -\rangle \ge 0$ for all $i \in [3]$, together with the two additional inequalities. These are obtained from the two divisors on ${\mathbb {P}}^2$ whose polyhedra of sections are shown in Fig. 3. Identifying the standard basis $e_i$ of ${\mathbb {Z}}^3 \cong {{\,\mathrm{Div}\,}}_{T_{\bar{M}}}({\mathbb {P}}^2)$ with specific divisors of ${\mathbb {P}}^2$ we add the inequalities $\langle -e_1-e_2, -\rangle \ge -1$ and $\langle -e_3, - \rangle \ge -1$ to those defining $Q_S$. We display the map $\iota$ in Fig. 4. Note that ${{\,\mathrm{TV}\,}}(\Sigma _S) \cong {\mathbb {P}}^2 \times {\mathbb {P}}^1$ and the image of $X_P$ is a hypersurface defined by a section of $L:= \mathcal {O}_{{\mathbb {P}}^2}(2) \boxtimes \mathcal {O}_{{\mathbb {P}}^1}(1)$. It is well known, for example by projecting to the ${\mathbb {P}}^2$ factor, that general members of the linear system defined by L are smooth del Pezzo surfaces of degree 5.

Fig. 4

Example of the piecewise linear map $\iota$

4 Full scaffoldings

In this section we introduce the notion of full scaffolding, and complete the proof of Theorem 1.1. If we fix a Fano polytope P, there are a vast number of possible scaffoldings, for many different shape varieties Z. We will control this class in two ways: first we constrain the class of polytopes to those which are cracked along the fan determined by Z; second we insist that our scaffoldings are full, which often uniquely determines a scaffolding on P with a given shape.

Definition 4.1

Given a Fano polytope $P \subset N_{\mathbb {R}}$ cracked along a fan $\Sigma$ in $M_{\mathbb {R}}$ we say a scaffolding S of P with shape $Z := {{\,\mathrm{TV}\,}}(\bar{\Sigma })$ is full if every vertical face of P is contained in a polytope $P_D+\chi$ for a (unique) element $(D,\chi ) \in S$.

Unfortunately full scaffoldings of a cracked polytope need not exist, and if they do exist, they need not be unique.

Example 4.2

Figure 5 shows a polygon P, which we attempt to scaffold using the shape $Z = {\mathbb {P}}^2$. We show the dual polygon on the right hand side of Fig. 5, from which we can easily see that P is cracked along the fan $\Sigma$ determined by Z. However the three vertical faces (the three edges of P whose normal directions are rays of $\Sigma$) of P cannot be covered by a single strut of a scaffolding, as shown.

Fig. 5

Cracked polytope with no full scaffolding

Remark 4.3

Note that in the case that the shape variety of Z is one-dimensional (that is, Z is isomorphic to ${\mathbb {P}}^1$) full scaffoldings for polytopes cracked along the fan defined by Z always exist. Indeed, vertical faces of P are precisely edges in the direction annihilating the minimal cone of $\Sigma$. Scaffold P by covering each such (vertical) edge with a single polytope $P_D+\chi$, and add any struts to cover each remaining vertex of P.

Proof of Theorem 1.1

We first show that if P is cracked along $\Sigma$, and admits a full scaffolding with shape $Z = {{\,\mathrm{TV}\,}}(\bar{\Sigma })$, then the tangent cone $\widetilde{C}_v$ to $Q_S$ at $\iota (v)$ is a unimodular cone for any $v \in {\text {verts}}\left( {P^\circ }\right)$.

Let C be the minimal cone of $\Sigma$ containing v. We let $k:= \dim C$, and $n_u:= \dim N_U$. We count the inequalities defining $\widetilde{C}_v$ given in Lemma 3.7. The description of $v^\star$ as a Cayley sum implies that there are k inequalities of the form $\langle \rho _s, - \rangle \ge -1$. Let $\bar{C}$ be the image of C in $\bar{\Sigma }$ and note that, since Z is smooth, there are $(k-n_u)$ rays of $\bar{C}$. Any ray generator of $\bar{\Sigma }$ which is not a ray of C defines an inequality $\langle (e_i,0), - \rangle \ge 0$ appearing in Lemma 3.7. Thus the total number of inequalities defining $\widetilde{C}_v$ is $(\ell - k + n_u) + k = \dim \widetilde{N}$, hence $\widetilde{C}_v$ is simplicial. Let $d:= \ell - k + n_u$.

Fixing a basis of $N_U$ we record the ray generators of $\widetilde{C}_v^\star$ in the columns of the matrix

$$\begin{aligned} \mathbb {M}= \begin{pmatrix} I_d &{}\quad A \\ 0 &{}\quad B. \end{pmatrix} \end{aligned}$$

We need to check that $\det (B) = \pm 1$. The last k columns of $\mathbb {M}$ are the vectors $\rho _s$ such that $u(s) \in v^\star$ for some $u \in {\text {verts}}\left( {S}\right)$. The last k rows of $\mathbb {M}$ correspond to vectors $e_i^\star \in \widetilde{M}$ dual to the divisors of Z determined by the k rays of $\bar{C}$. Let $b_i$ for $i \in [k]$ denote the ray generators of C. Fixing a $u \in {\text {verts}}\left( {S}\right)$ such that $v \in C_u$;

$$\begin{aligned} \langle \rho _s, e^\star _i\rangle&= \langle \rho _s, \iota _u(b_i)\rangle \\&= \langle u(s), b_i \rangle , \end{aligned}$$

by Lemma 3.5. Varying s we see that these values are nothing other than the co-ordinates of the standard simplex $\Delta _{k-1}$, the image of $v^\star \rightarrow {\mathbb {R}}^k$ defined by its description as a Cayley sum.

Conversely, assume that $\widetilde{C}_v$ is unimodular for every vertex $v \in {\text {verts}}\left( {P^\circ }\right)$. It immediately follows from Proposition 3.6 that $P^\circ$ is cracked along $\Sigma$. To see that scaffolding must be full we note that for each strut $s = (D,\chi )$ such that $u(s) \in v^\star$ the intersection $(P_D+\chi ) \cap v^\star$ is contained in a single vertical face. If none of the inequalities appearing in Lemma 3.7 are redundant then it follows from the count of these inequalities made above that there must be a single strut covering each vertical face.

Note that the inequalities $\langle e_i, - \rangle \ge 0$ clearly cannot be redundant; so we check for redundancy among the inequalities $\langle \rho _s, -\rangle \ge -1$. Given a point $p \in C_u$ it follows from Lemma 3.5 that $\langle \rho _s,\iota (p)\rangle = \langle u(s), p\rangle$ for any $u \in {\text {verts}}\left( {S}\right)$. However, for some $u \in {\text {verts}}\left( {S}\right)$, $w:= u(s)$ is a vertex of $v^\star$. Moreover, we have assumed that s is the only element of S such that $w \in P_D+\chi$. The vertex w defines a facet of $C_u$, and since $\langle w,-\rangle \ge -1$ is not redundant in defining $C_u$ the inequality $\langle \rho _s,-\rangle$ is not redundant in defining $\iota (C_u)$, and hence $\widetilde{C}_v$. $\square$

5 Smoothing complete intersections

We now restrict our attention to scaffoldings of polytopes cracked along the fan of a product of projective spaces. As shown in [10], the embeddings obtained through this construction express $X_P$ as a complete intersection inside $Y_S$.

Proposition 5.1

Given a cracked polytope P and a full scaffolding S of P with shape

$$\begin{aligned} Z = {\mathbb {P}}^{k_1}\times \cdots \times {\mathbb {P}}^{k_r}, \end{aligned}$$

the image of $X_P \hookrightarrow Y_S$ is a complete intersection.

Proof

The homogeneous co-ordinate ring of $Y_S$ is generated by variables $x_{i,j}$ for $i \in [r]$, $j \in [k_i]$, and variables $y_s$ for $s \in S$. Let $e_{i,j}$ denote the standard basis vector in ${{\,\mathrm{Div}\,}}_{T_{\bar{M}}}Z$ corresponding to $x_{i,j}$. The sublattice $\theta (N) \subset \widetilde{N}$ is the intersection of the hyperplanes

$$\begin{aligned} H_i:= \Big \{v \in \widetilde{N}: \big \langle \sum _{j \in [k_i]}{e^\star _{i,j}}, v \big \rangle = 0\Big \}, \end{aligned}$$

for $i \in [r]$. Thus $X_P$ is cut out by the equations

$$\begin{aligned} \prod _{j \in [k_i]}{x_{i,j}} = \prod _{s \in S}y_s^{-\sum _{j \in [k_i]}\langle \rho _s,e^\star _{i,j}\rangle }. \end{aligned}$$

It is easily seen that these equations generate the toric ideal of the image of $X_P$ in the affine chart defined by $\widetilde{C}_v$, for any $v \in {\text {verts}}\left( {P^\circ }\right)$. $\square$

We fix Z for the remainder of this section to be the product of projective spaces ${\mathbb {P}}^{k_1}\times \cdots \times {\mathbb {P}}^{k_r}$. We let $\bar{\Sigma }$ be the fan determined by Z, and fix a splitting $N = N_U \oplus \bar{N}$. If S is a scaffolding with shape Z, we define

$$\begin{aligned} L_i:= \mathcal {O}_{Y_S}\Big (\big \{\prod _{j \in [k_i]}{x_{i,j} = 0}\big \}\Big ) \in {{\,\mathrm{Pic}\,}}Y_S. \end{aligned}$$

In particular, we can describe $X_P$ by intersecting vanishing loci of (binomial) sections of the line bundles $L_i$ on $Y_S$.

Remark 5.2

In fact, following [10], scaffolding with shape Z isomorphic to any toric tower of projective space bundles will express $X_P$ in $Y_S$ as a complete intersection. Our restriction to the product of projective spaces case is a simplifying one, but we expect results to hold true in the more general context.

We first introduce an important ingredient, the notion of a slab. This terminology is taken from the work of Gross–Siebert [16], though our context and definition differ slightly. In particular our definition is closer to that of a naked slab since we do not yet decorate them with particular slab functions.

Definition 5.3

Given a scaffolding S of a Fano polytope P, we define the collection slabs to be the collection of polytopes formed by intersecting codimension one cones of $\Sigma$ with $P^\circ$.

We index the slabs in $P^\circ$ by indexing the torus invariant curves in Z.

Lemma 5.4

The codimension one cones of $\Sigma$ are in bijection with functions

$$\begin{aligned} f:[r+1] \rightarrow \coprod _{i \in [r]}[k_i], \end{aligned}$$

such that $f(i) \in [k_i]$, and we define $i_\mathfrak {s}\in [r]$ to be the index such that $f(r+1) \in [k_{i_\mathfrak {s}}]$.

Given a slab $\mathfrak {s}$, we denote the toric variety defined by its normal fan as $X_\mathfrak {s}$. Note that, as P is cracked, $X_\mathfrak {s}$ is smooth.

Lemma 5.5

Fix a Fano polytope P and a slab $\mathfrak {s}= \sigma \cap P^\circ$, where $\sigma$ is a codimension one cone of $\Sigma$. Let f be the function associated to $\mathfrak {s}$ by Lemma 5.4. $X_\mathfrak {s}$ is isomorphic to the toric stratum of $Y_S$ defined by the intersection of the vanishing loci $\{x_{i,f(i)} = 0\}$, for $i \in [r]$ and the vanishing locus $\{x_{i_\mathfrak {s},f(r+1)}\}$.

Proof

This follows immediately from Lemma 5.4 and the fact that

$$\begin{aligned} \iota (\mathfrak {s}) = {{\,\mathrm{Ann}\,}}\big ( \{e_{i,f(i)}: i \in [r]\} \cup \{e_{i_\mathfrak {s},f(r+1)}\} \big ) \cap Q_S. \end{aligned}$$

$\square$

We let $\mu _\mathfrak {s}:X_\mathfrak {s}\rightarrow Y_S$ denote the inclusion corresponding to the inclusion of $\mathfrak {s}\hookrightarrow Q_S$. Each slab $\mathfrak {s}$ corresponds to a curve $C_\mathfrak {s}$ in Z. The index $i_\mathfrak {s}$ appearing in Lemma 5.4 is the unique $i \in [r]$ such that $C_\mathfrak {s}$ projects to a curve under the map $Z \rightarrow {\mathbb {P}}^{k_{i_\mathfrak {s}}}$.

Definition 5.6

Fix a scaffolding S of a reflexive polytope P, and a slab $\mathfrak {s}\subset P^\circ$. Given a facet $\tau$ of $\mathfrak {s}$ contained in $\partial P^\circ$ we let $D_\tau$ denote the divisor of $X_\mathfrak {s}$ corresponding to the facet $\tau$, and we define

$$\begin{aligned} a_\tau := \begin{array}{l@{\quad }l} \ell (\tau ^\star ) &{} \text {if }\tau \text { is a face of }P^\circ \text {, and }\dim \tau ^\star = 1\\ 0 &{} \text {otherwise,} \end{array} \end{aligned}$$

where $\ell (e)$ denotes the lattice length of the edge e. We define the slab divisor

$$\begin{aligned} D_\mathfrak {s}:= \sum _{\tau }{a_\tau D_{\tau }}, \end{aligned}$$

where the sum is taken over facets $\tau$ of $\mathfrak {s}$ contained in $\partial P^\circ$. Moreover we let $L_\mathfrak {s}$ denote the line bundle $\mathcal {O}(D_\mathfrak {s}) \in {{\,\mathrm{Pic}\,}}(X_\mathfrak {s})$ for each slab $\mathfrak {s}$.

Remark 5.7

Note that in Definition 5.6 we assume that P is reflexive. In fact this definition can be extended to all Fano polytopes, but becomes more complicated and we omit it here.

Note that sections of $L_\mathfrak {s}$ are closely analogous to the slab functions appearing in [16]. We relate the line bundles $L_\mathfrak {s}$ with the bundles $L_i$ defining the image of $X_P$ in $Y_S$.

Lemma 5.8

Fix a polytope P cracked along the fan $\Sigma$, and S a full scaffolding of P with shape Z. Given a slab $\mathfrak {s}$, we have that $L_\mathfrak {s}= \mu _\mathfrak {s}^\star L_{i_\mathfrak {s}}$.

Proof

Let $\Sigma _\mathfrak {s}$ denote the fan determined by $X_\mathfrak {s}$. Observe that

$$\begin{aligned} \mathbf {y}_\mathfrak {s}:= \prod _{s \in S}y_s^{-\sum _{j \in [k_{i_\mathfrak {s}}]}\langle \rho _s,e^\star _{i_\mathfrak {s},j}\rangle } \in \Gamma (Y_S,L_{i_\mathfrak {s}}). \end{aligned}$$

Moreover recall that there is a bijection between the facets $\tau$ of $\mathfrak {s}$ contained in $\partial P^\circ$ and the set

$$\begin{aligned} \{s \in S: \langle \rho _s, - \rangle \ge -1 \text { defines a facet of }\mathfrak {s}\}. \end{aligned}$$

Thus the pullback of $\{ \mathbf {y}_\mathfrak {s}= 0\}$ to $X_\mathfrak {s}$ is the divisor obtained by labelling each such $\rho _s$ with the integer $\sum _{j \in [k_{i_\mathfrak {s}}]}\langle -\rho _s,e^\star _{i_\mathfrak {s},j}\rangle$. We now interpret this integer as an edge length.

Observe that ${{\,\mathrm{Pic}\,}}(Z) \cong {\mathbb {Z}}^r$, and that the map $\nu$ in the short exact sequence

$$\begin{aligned} 0 \rightarrow N {\mathop {\rightarrow }\limits ^{\theta }} \widetilde{N} {\mathop {\rightarrow }\limits ^{\nu }} {{\,\mathrm{Pic}\,}}(Z) \rightarrow 0, \end{aligned}$$

sends $x \in \widetilde{N}$ to $\sum _{i \in [r]}{a_i\bar{e}_i}$, where $\bar{e}_i$ is the pullback of the hyperplane class of ${\mathbb {P}}^{k_i}$ to Z along the canonical projection, and

$$\begin{aligned} a_i:= \sum _{j \in [k_{i}]}\langle x,e^\star _{i,j}\rangle . \end{aligned}$$

Writing $x = (D,\chi ) \in {{\,\mathrm{Div}\,}}_{T_{\bar{M}}}Z \oplus N_U$, the polytope $P_D \cong \prod _{i \in [r]}a_i\Delta _{k_i}$ is a product of dilated standard simplices. Note that each edge in the ith factor has length $a_i$. Thus the coefficient attached to each $\rho _s$ defining a facet $\tau$ of $\mathfrak {s}$ is precisely the edge length $\ell (\tau ^\star )$ of $P_D$ corresponding to $C_\mathfrak {s}$, where $s = (D,\chi )$. $\square$

Definition 5.9

Given a reflexive polytope P, cracked along a fan $\Sigma$, and a scaffolding S of P, we say S is positive if the image of $\Gamma (Y_S,L_{i_\mathfrak {s}}) \rightarrow \Gamma (X_\mathfrak {s},L_\mathfrak {s})$ is a basepoint free linear system for all slabs $\mathfrak {s}$.

Remark 5.10

It would appear more natural, and closer to the definition appearing in [16], to insist only that the complete linear system $\Gamma (X_\mathfrak {s},L_\mathfrak {s})$ is basepoint free. Note however that this condition is independent of S, while Definition 5.9 is not. We conjecture that if the linear system $\Gamma (X_\mathfrak {s},L_\mathfrak {s})$ is basepoint free for all $\mathfrak {s}$ then a smoothing of $X_P$ exists. Our slightly more restrictive definition guarantees the existence of an embedded smoothing in $Y_S$.

Conjecture 5.11

Fix a unimodular rational fan $\Sigma$ in $M_{\mathbb {R}}$ such that $Z \in {{\,\mathrm{TV}\,}}(\bar{\Sigma })$ is projective, and a polytope P such that $P^\circ$ is cracked along $\Sigma$. If $\Gamma (X_\mathfrak {s},L_\mathfrak {s})$ is basepoint free for all slabs $\mathfrak {s}$, then $X_P$ admits a smoothing.

We study the equations defining $X_P \subset Y_S$ in the toric affine chart of $Y_S$ with cone dual to $\widetilde{C}_v$ for a given vertex $v \in {\text {verts}}\left( {P^\circ }\right)$. Let $S(v) \subset S$ denote those $s \in S$ such that the inequality $\langle \rho _s,-\rangle \ge -1$ appears in Lemma 3.7 as a defining inequality for $\widetilde{C}_v$. Let $B(v) = \coprod _{i \in [r]}B_i(v)$ denote the set of vectors $e_{i,j}$ dual to vectors $e^\star _{i,j}$ which are not contained in the minimal cone of $\Sigma$ containing v. In this notation, restricting the equations defining $X_P \subset Y_S$ to ${{\,\mathrm{Spec}\,}}\mathbb {k}[(\widetilde{C}_v-v)\cap \widetilde{M}]$, we obtain the equations:

$$\begin{aligned} \prod _{j \in B_i(v)}{x_{i,j}} = \prod _{s \in S(v)}{y^{l_{i,s}}_s}~\text {for all }i \in [r] \end{aligned}$$

(1)

where

$$\begin{aligned} l_{i,s}:= {-\sum _{j \in [k_i]}\langle \rho _s,e^\star _{i,j}\rangle }. \end{aligned}$$

We now prove the first part of Theorem 1.2, namely that vanishing locus of a general section of $\bigoplus _{i \in [r]} L_i$ is a smooth variety.

Proof of Theorem 1.2

(i) Fix a point $x \in {{\,\mathrm{Im}\,}}{{\,\mathrm{Sing}\,}}(X_P) \subset Y_S$ and let $p \in \partial P^\circ$ denote its moment map image. Let C be the minimal cone of $\Sigma$ containing p. The cone C corresponds to a toric stratum $X_C$ of Z, the product of toric strata $X_i$ of ${\mathbb {P}}^{k_i}$ for $i \in [r]$. Let v be a vertex of the minimal face of $P^\circ$ containing p, so that $x \in {{\,\mathrm{Spec}\,}}\mathbb {k}[(\widetilde{C}_v - v)\cap \widetilde{M}]$. We replace $Y_S$ by a resolution, or by the complement of ${{\,\mathrm{Sing}\,}}Y_S$; by Theorem 1.1 this can be done in the complement of a Zariski neighbourhood of $x \in Y_S$.

Let V denote the variety cut out by the Eq. (1) such that $X_i$ is zero dimensional. Since $B_i(v)$ is a singleton for each such equation, this equation becomes $x_{i,j} = \prod _{s \in S(v)}{y^{l_{i,s}}_s}$ for some $j \in [k_i]$. Thus the variety V is smooth as $\widetilde{C}_v$ is unimodular.

If $X_i$ is not zero dimensional $x \in {{\,\mathrm{Im}\,}}X_{\mathfrak {s}}$ (and $p \in \mathfrak {s}$) for all the slabs $\mathfrak {s}$ corresponding to curves of Z contained in $X_i$. Consider the first value i such that $|B_i(v)|>1$, then $L_i$ is basepoint free on $X_\mathfrak {s}$, and hence in a neighbourhood of $x \in Y_S$. It follows from a version of Bertini’s theorem over $\mathbb {k}$ that since V is smooth and affine (and hence quasi-projective) the singularities of the vanishing locus of a general section of $L_i$ on V are contained in the base locus of $L_i$. Removing the base locus of $L_i$ on X and inductively applying this version of Bertini’s theorem we obtain that the vanishing locus of a general section of $\bigoplus _{i \in [r]}{L_i}$ is smooth in a neighbourhood of x. Since x was chosen arbitrarily from the singularities of $X_P$, and applying a standard compactness argument, we see that perturbing the Eq. (1) smooth $X_P$ in $Y_S$. $\square$

We now construct the divisor $D_S$ appearing in the statement of Theorem 1.2.

Definition 5.12

Let $D_S$ be the divisor in $Y_S$ corresponding to function on the rays of the normal fan to $Q_S$ which sends each ray generated by $\rho _s$ for some $s \in S$ to 1.

We can now conclude the proof of Theorem 1.2 by describing the restriction of the divisor $D_S$ to a smoothing of $X_P$. The strategy is broadly the same: for each equation in (1) we can either eliminate it, or make a transversality argument based on the positivity of S.

Proof of Theorem 1.2

(ii) Let X be a general smoothing of $X_P$ obtained by perturbing Eq. (1). Recall that $\prod _{j \in [k_i]}{x_{i,j}} \in \Gamma (Y_S,L_i)$ for each $i\in [r]$. Thus the restriction of $D_S$ to X (or $X_P$) is anti-canonical by the adjunction formula.

To show that the restriction of $D_S$ to X is simple normal crossings (snc) we must show that each component of $D_S|_X$ is smooth, and $D_S|_X$ is locally of the form $\prod _{i \in [a]}{x_i} = 0$, where $x_i$ are local parameters on $Y_S$ and $a \in [\dim N]$. The argument used to show that $X_P$ smooths inside $Y_S$ extends immediately to each component $\{y_s = 0\} \cap X_P$, ensuring each component of $D_S|_X$ is smooth.

Fix a point $x \in X_P$ such that the image of x in $Y_S$ lies at the intersection of divisors $\{y_s = 0\} \cap {{\,\mathrm{Im}\,}}X_P$ for $s \in S' \subseteq S$, where $S'$ is some subset of S. Let p be point in $P^\circ$ corresponding to x, and let $v \in {\text {verts}}\left( {P^\circ }\right)$ be a vertex of the minimal face of $P^\circ$ containing p. As above the local affine piece,

$$\begin{aligned} Y_v:= {{\,\mathrm{Spec}\,}}\mathbb {k}[(\widetilde{C}_v-v) \cap \widetilde{M}], \end{aligned}$$

has co-ordinates $y_s$ for $s \in S(v)$—noting that $S' \subseteq S(v) \subseteq S$—and $x_{i,j}$ where $e_{i,j} \in B(v)$. The restriction of the divisor $D_S$ to $Y_v$ is given by the equation $\prod _{s \in S(v)}{y_s = 0}$. This divisor remains snc after intersection with the ith Eq. (1) if $|B_i(v)| = 1$ (with co-ordinates on the vanishing locus given by eliminating $x_{i,j}$, where $B_i(v) = \{e_{i,j}\}$). As above, if $|B_i(v)| > 1$, the base locus of $L_i$ is disjoint from a neighbourhood of x. Thus, inductively applying the fact that the sum of an snc divisor and a general member of a free linear system is snc—see [18, Lemma 9.1.9]—the result follows. $\square$

6 Examples

We consider examples in dimension 3, using the famous classifications of reflexive 3-polytopes by Kreuzer–Skarke [17], and of three dimensional Fano varieties by Mori–Mukai [19, 20].

Example 6.1

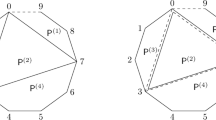
We construct a Fano variety in the family 2–18 in the Mori–Mukai list from a cracked polytope. The complete intersection description we obtain appears in [7]. Let $N:= {\mathbb {Z}}^3$, $N_U := \langle e_3\rangle$, and $\bar{N}:= {\mathbb {Z}}^2 = \langle e_1,e_2\rangle$. We let $Z:= {\mathbb {P}}^2$, and let $\Sigma$ denote the corresponding fan. The left hand image in Fig. 6 shows the scaffolding of P using 3 struts: a pair of triangles labelled $s_1$ and $s_2$, and the remaining vertex. The right hand image shows $P^\circ$ cracked into three Cayley polytopes, two of which ($Q_2$ and $Q_3$) are Cayley sums of a pair of triangles, while $Q_1$ is the Cayley sum of three line segments. Note that $X_P$ is a hypersurface in $Y_S$, the vanishing locus of a section of some $L \in {{\,\mathrm{Pic}\,}}Y_S$.

We check positivity along the slab $\mathfrak {s}= Q_1 \cap Q_3$. Observe that $X_\mathfrak {s}\cong \mathbb {F}_1$, and let $\pi :\mathbb {F}_1 \rightarrow {\mathbb {P}}^2$ be the contraction of the $(-1)$-curve. We have that $L_\mathfrak {s}= \pi ^\star {\mathcal {O}_{{\mathbb {P}}^2}(2)}$, which is a basepoint free divisor and, verify that in this example the map $\Gamma (Y_S,L) \rightarrow \Gamma (X_\mathfrak {s},L_\mathfrak {s})$ is surjective.

The toric variety $Y_S$ admits a morphism to ${\mathbb {P}}^2\times {\mathbb {P}}^1$, realising a smoothing X of $X_P$ as a double cover of ${\mathbb {P}}^2 \times {\mathbb {P}}^1$ branched in a divisor of bidegree (2, 2); see [7] for more details.

Fig. 6

Construction of a variety in the family 2–18 via a cracked polytope

Example 6.2

We describe an important class of non-examples. Consider the reflexive polytope P with PALP id 15, whose corresponding toric variety $X_P$ is shown to be non-smoothable by Petracci [22]. A neighbourhood of ${{\,\mathrm{Sing}\,}}X_P$ is isomorphic to a bundle of $A_1$ (surface) singularities over ${\mathbb {P}}^1$. This is represented on P by an edge of length 2 which has direction vector $u := (0,1,1)$. $P^\circ$ is cracked along the fan $\Sigma$ consisting of two half spaces meeting along $M_U = {{\,\mathrm{Ann}\,}}(u) \subset M_{\mathbb {R}}$. As observed in Remark 4.3 this polytope admits a full scaffolding with shape ${\mathbb {P}}^1$. However this scaffolding is not positive.

Fig. 7

Slab divisor for a non-positive scaffolding

The unique slab $\mathfrak {s}= {{\,\mathrm{Ann}\,}}(u) \cap P^\circ$ is shown in Fig. 7, together with the divisor $D_\mathfrak {s}$. The toric variety $X_\mathfrak {s}\cong \mathbb {F}_1$ with $(-1)$-curve E, and $D_\mathfrak {s}= 2E$; hence S cannot be positive. The same analysis applies to the reflexive polytopes with PALP ids in the set (a subset of the list appearing in [22]),

$$\begin{aligned} \{16,58,59,61,65,66,192,193,197\}. \end{aligned}$$

That is, the corresponding (dual) polytopes are cracked along the hyperplane dual to the direction u of an edge defining a transverse $A_n$ singularity. However no full scaffolding of these polytopes is positive, as $L_\mathfrak {s}$—where $\mathfrak {s}= {{\,\mathrm{Ann}\,}}(u) \cap P^\circ$—is a multiple of a curve with negative self intersection.