Abstract
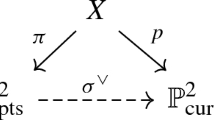
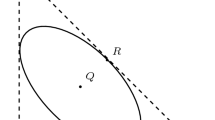
In this work we study the additive orbifold cohomology of the moduli stack of smooth genus g curves. We show that this problem reduces to investigating the rational cohomology of moduli spaces of cyclic covers of curves where the genus of the covering curve is g. Then we work out the case of genus g = 3. Furthermore, we determine the part of the orbifold cohomology of the Deligne–Mumford compactification of the moduli space of genus 3 curves that comes from the Zariski closure of the inertia stack of \({\mathcal{M}3}\) .
Similar content being viewed by others
References
Abramovich D., Corti A., Vistoli A.: Twisted bundles and admissible covers. Special issue in honor of Steven L. Kleiman. Commun. Algebra 31(8), 3547–3618 (2003)
Abramovich, D., Graber, T., Vistoli, A.: Algebraic orbifold quantum products. In: Orbifolds in Mathematics and Physics (Madison, WI, 2001), Contemp. Math., vol. 310, pp. 1–24. American Mathematical Society, Providence (2002)
Abramovich D., Graber T., Vistoli A.: Gromov–Witten theory of Deligne–Mumford stacks. Am. J. Math. 130(5), 1337–1398 (2008)
Abramovich D., Vistoli A.: Compactifying the space of stable maps. J. Am. Math. Soc. 15(1), 27–75 (2002)
Bayer A., Cadman C.: Quantum cohomology of [C N/μ r ]. Compos. Math. 146(5), 1291–1322 (2010)
Bernstein, M.: Moduli of curves with level structure. Ph.D. Thesis, Harvard University (1999)
Cadman C.: Using stacks to impose tangency conditions on curves. Am. J. Math. 129(2), 405–427 (2007)
Catanese, F.: Irreducibility of the space of cyclic covers of algebraic curves of fixed numerical type and the irreducible components of \({Sing (\bar{\mathfrak M_g})}\) . arXiv:1011.0316v1
Chen W., Ruan Y.: A new cohomology theory of orbifold. Commun. Math. Phys. 248(1), 1–31 (2004)
Cornalba M.: On the locus of curves with automorphisms. Ann. Mat. Pura Appl. 149(4), 135–151 (1987)
Dolgachev, I.V.: Classical Algebraic Geometry. A Modern View, vol. xii. Cambridge University Press, Cambridge (2012)
Edmonds A.L.: Surface symmetry. I. Mich. Math. J. 29(2), 171–183 (1982)
Fantechi, B.: Private communication (2008)
Getzler, E.: Operads and moduli of genus 0 Riemann surfaces. In: The Moduli Space of Curves (Texel Island, 1994), Progr. Math., vol. 129, pp. 199–230. Birkhäuser Boston, Boston (1995)
Getzler, E.: Topological recursion relations in genus 2. In: Integrable Systems and Algebraic Geometry (Kobe/Kyoto, 1997), vol. 73–106. World Scientific Publishing, River Edge (1998)
Grothendieck A.: Sur quelques points d’algèbre homologique (French). Tôhoku Math. J. 9(2), 119–221 (1957)
Kisin M., Lehrer G.I.: Equivariant Poincaré polynomials and counting points over finite fields. J. Algebra 247(2), 435–451 (2002)
Knudsen F.F.: Projectivity of the moduli space of stable curves II. The stacks \({\overline{M}_{g,n}}\) . Math. Scand. 52, 161–199 (1983)
Krug, S.: Rational cohomology of \({\bar R_2}\) (and \({\bar S_2)}\) . arXiv:1012.5191v1
Looijenga, E.; Cohomology of \({\mathcal{M}_3}\) and \({{\mathcal {M}^1_3}}\) . In: Mapping Class Groups and Moduli Spaces of Riemann Surfaces (Göttingen, 1991/Seattle, WA, 1991), Contemp. Math., vol. 150, pp. 205–228. American Mathematical Society, Providence (1993)
Pagani, N.: Chen–Ruan cohomology of \({\mathcal{M}_{1,n}}\) and \({\overline{\mathcal{M}}_{1,n}}\) . To appear in Ann. Inst. Fourier (Grenoble) 63 (2013)
Pagani N.: The Chen–Ruan cohomology of moduli of curves of genus 2 with marked points. Adv. Math. 229(3), 1643–1687 (2012)
Pagani, N.: The orbifold cohomology of moduli of hyperelliptic curves. Int. Math. Res. Not. 2012(10):2163–2178 (2012)
Pardini R.: Abelian covers of algebraic varieties. J. Reine Angew. Math. 417, 191–213 (1991)
Peters, C.A.M., Steenbrink, J.H.M.: Mixed Hodge Structures. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, 52. Springer, Berlin (2008)
Spencer, J.E.: The orbifold cohomology of the moduli of genus-two curves. In: Gromov-Witten theory of spin curves and orbifolds, Contemp. Math., vol. 403, 167–184. American Mathematical Society, Providence (2006)
Tommasi O.: Rational cohomology of the moduli space of genus 4 curves. Compos. Math. 141(2), 359–384 (2005)
Tommasi O.: Rational cohomology of M 3,2. Compos. Math. 143(4), 986–1002 (2007)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Pagani, N., Tommasi, O. The orbifold cohomology of moduli of genus 3 curves. manuscripta math. 142, 409–437 (2013). https://doi.org/10.1007/s00229-013-0608-z
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00229-013-0608-z