The Power Word Problem in Graph Products

Abstract

The power word problem for a group $\varvec{G}$ asks whether an expression $\varvec{u_1^{x_1} \cdots u_n^{x_n}}$, where the $\varvec{u_i}$ are words over a finite set of generators of $\varvec{G}$ and the $\varvec{x_i}$ binary encoded integers, is equal to the identity of $\varvec{G}$. It is a restriction of the compressed word problem, where the input word is represented by a straight-line program (i.e., an algebraic circuit over $\varvec{G}$). We start by showing some easy results concerning the power word problem. In particular, the power word problem for a group $\varvec{G}$ is $\varvec{\textsf{uNC}^{1}}$-many-one reducible to the power word problem for a finite-index subgroup of $\varvec{G}$. For our main result, we consider graph products of groups that do not have elements of order two. We show that the power word problem in a fixed such graph product is $\varvec{\textsf{AC} ^0}$-Turing-reducible to the word problem for the free group $\varvec{F_2}$ and the power word problems of the base groups. Furthermore, we look into the uniform power word problem in a graph product, where the dependence graph and the base groups are part of the input. Given a class of finitely generated groups $\varvec{\mathcal {C}}$ without order two elements, the uniform power word problem in a graph product can be solved in $\varvec{\textsf{AC} ^0[\textsf{C}_=\textsf{L} ^{{{\,\textrm{UPowWP}\,}}(\mathcal {C})}]}$, where $\varvec{{{\,\textrm{UPowWP}\,}}(\mathcal {C})}$ denotes the uniform power word problem for groups from the class $\varvec{\mathcal {C}}$. As a consequence of our results, the uniform knapsack problem in right-angled Artin groups is $\varvec{\textsf{NP}}$-complete. The present paper is a combination of the two conference papers (Lohrey and Weiß 2019b, Stober and Weiß 2022a). In Stober and Weiß (2022a) our results on graph products were wrongly stated without the additional assumption that the base groups do not have elements of order two. In the present work we correct this mistake. While we strongly conjecture that the result as stated in Stober and Weiß (2022a) is true, our proof relies on this additional assumption.

1 Introduction

Algorithmic problems in group theory have a long tradition, going back to the work of Dehn from 1911 [13]. One of the fundamental group theoretic decision problems introduced by Dehn is the word problem for a finitely generated group G (with a fixed finite generating set $\Sigma$): does a given word $w \in \Sigma ^*$ evaluate to the group identity? Novikov [55] and Boone [11] independently proved in the 1950’s the existence of finitely presented groups with undecidable word problem. On the positive side, in many important classes of groups the word problem is decidable, and in many cases also the computational complexity is quite low. Famous examples are finitely generated linear groups, where the word problem belongs to deterministic logarithmic space ($\textsf{L}$ for short) [37] and hyperbolic groups where the word problem can be solved in linear time [30] as well as in $\textsf{LOGCFL}$ [38].

In recent years, also compressed versions of group theoretical decision problems, where input words are represented in a succinct form, have attracted attention. One such succinct representation are so-called straight-line programs, which are context-free grammars that produce exactly one word. The size of such a grammar can be much smaller than the word it produces. For instance, the word $a^n$ can be produced by a straight-line program of size $\mathcal {O}(\log n)$. For the compressed word problem for the group G the input consists of a straight-line program that produces a word w over the generators of G and it is asked whether w evaluates to the identity element of G. This problem is a reformulation of the circuit evaluation problem for G. The compressed word problem naturally appears when one tries to solve the word problem in automorphism groups or semidirect products [39, Section 4.2]. For the following classes of groups, the compressed word problem is known to be solvable in polynomial time: finite groups (where the compressed word problem is either P-complete or in $\textsf{uNC}^{2}$ [9]), finitely generated nilpotent groups [35] (where the complexity is even in $\textsf{uNC}^{2}$), hyperbolic groups [31] (in particular, free groups), and virtually special groups (i.e, finite extensions of subgroups of right-angled Artin groups) [39]. The latter class covers for instance Coxeter groups, one-relator groups with torsion, fully residually free groups and fundamental groups of hyperbolic 3-manifolds. For finitely generated linear groups there is a randomized polynomial time algorithm for the compressed word problem [39, 41]. Simple examples of groups where the compressed word problem is intractable are wreath products $G \wr \mathbb {Z}$ with G finite non-solvable: for every such group the compressed word problem is $\textsf{PSPACE}$-complete [8], whereas as the (ordinary) word problem for $G \wr \mathbb {Z}$ is in $\textsf{uNC}^{1}$ [61].

In this paper, we study a natural restriction of the compressed word problem called the power word problem. An input for the power word problem for the group G is a tuple $(u_1, x_1, u_2, x_2, \ldots , u_n, x_n)$ where every $u_i$ is a word over the group generators and every $x_i$ is a binary encoded integer (such a tuple is called a power word); the question is whether $u_1^{x_1} u_2^{x_2}\cdots u_n^{x_n}$ evaluates to the group identity of G. This problem naturally arises in the context of the so-called knapsack problem; we will explain more about this later.

From a power word $(u_1, x_1, u_2, x_2, \ldots , u_n, x_n)$ one can easily (e. g., by an $\textsf{uAC}^{0}$-reduction) compute a straight-line program for the word $u_1^{x_1} u_2^{x_2}\cdots u_n^{x_n}$. In this sense, the power word problem is at most as difficult as the compressed word problem. On the other hand, both power words and straight-line programs achieve exponential compression in the best case; so the additional difficulty of the compressed word problem does not come from a higher compression rate but rather because straight-line programs can generate more “complex” words.

Our main results for the power word problem are the following; in each case we compare our results with the corresponding results for the compressed word problem:¹

• The power word problem for every finitely generated nilpotent group is in $\textsf{uTC}^{0}$ and hence has the same complexity as the word problem (or the problem of multiplying binary encoded integers). The proof is a straightforward adaption of a proof from [52]. There, the special case, where all words $u_i$ in the input power word are single generators, was shown to be in $\textsf{uTC}^{0}$. The compressed word problem for every finitely generated nilpotent group belongs to the class $\textsf{DET} \subseteq \textsf{uNC}^{2}$ and is hard for the counting class $\textsf{C}_{=}\textsf{L}$ in case of a torsion-free nilpotent group [35].

• The power word problem for the Grigorchuk group is $\textsf{uAC} ^0$-many-one-reducible to its word problem. Since the word problem for the Grigorchuk group is in $\textsf{L}$ [8, 23], also the power word problem is in $\textsf{L}$. Moreover, in [8], it is shown that the compressed word problem for the Grigorchuk group is $\textsf{PSPACE}$-complete. Hence, the Grigorchuk group is an example of a group for which the compressed word problem is provably more difficult than the power word problem. Note that, while the word problem of the Grigorchuk group can be solved in linear time [50], we do not know whether this also applies to the power word problem.

• The power word problem for a finitely generated group G is $\textsf{uNC}^{1}$-many-one-reducible to the power word problem for any finite index subgroup of G. An analogous result holds for the compressed word problem as well [35].

• If G is a graph product of finitely generated groups $G_1, \ldots , G_n$ (the so-called base groups) not containing any elements of order two, then the power word problem in G can be decided in $\textsf{uAC} ^0$ with oracle gates for (i) the word problem for the free group $F_2$ and (ii) the power word problems for the base groups $G_i$. In order to define a graph product of groups $G_1, \ldots , G_n$, one needs a graph with vertices $1, \ldots , n$. The corresponding graph product is obtained as the quotient of the free product of $G_1, \ldots , G_n$ modulo the commutation relations that allows elements of $G_i$ to commute with elements of $G_j$ iff i and j are adjacent in the graph. Graph products were introduced by Green in 1990 [25]. The compressed word problem for a graph product is polynomial time Turing-reducible to the compressed word problems for the base groups [28].

• A right-angled Artin group (RAAG) can be defined as a graph product of copies of $\mathbb {Z}$. As a corollary of our transfer theorem for graph products, it follows that the power word problem for a RAAG can be decided in $\textsf{uAC} ^0$ with oracle gates for the word problem for the free group $F_2$. The same upper complexity bound was shown before by Kausch [33] for the ordinary word problem for a RAAG and in [43] for the power word problem for a finitely generated free group. As a consequence of our new result, the power word problem for a RAAG is in $\textsf{L}$ (for the ordinary word problem this follows from the well-known fact that RAAGs are linear groups together with the above mentioned result of Lipton and Zalcstein [37]). The compressed word problem for every RAAG is in P (polynomial time) and P-complete if the RAAG is non-abelian [39].

In all the above mentioned results, the group is fixed, i.e., not part of the input. In general, it makes no sense to input an arbitrary finitely generated group, since there are uncountably many such groups. On the other hand, if we restrict to finitely generated groups with a finitary description, one may also consider a uniform version of the word problem/power word problem/compressed word problem, where the group is part of the input. We will consider the uniform power word problem for graph products for a fixed countable class $\mathcal {C}$ of finitely generated groups. We assume that the groups in $\mathcal {C}$ have a finitary description.² Then a graph product is given by a list $G_1, \ldots G_n$ of base groups from $\mathcal {C}$ together with an undirected graph on the indices $1, \ldots , n$. For this setting Kausch [33] proved that the uniform word problem for graph products belongs to $\textsf{C}_=\textsf{L} ^{{{\,\textrm{UWP}\,}}(\mathcal {C})}$, i.e., the counting logspace class $\textsf{C}_=\textsf{L}$ with an oracle for the uniform word problem for the class $\mathcal {C}$ (we write ${{\,\textrm{UWP}\,}}(\mathcal {C})$ for the latter). We extend this result to the power word problem under the additional assumption that no group in $\mathcal {C}$ contains an element of order two. More precisely, we show that the uniform power word problem for graph products over that class $\mathcal {C}$ of base groups belongs to the closure of $\textsf{C}_=\textsf{L} ^{{{\,\textrm{UPowWP}\,}}(\mathcal {C})}$ under $\textsf{uAC} ^0$-Turing-reductions, where ${{\,\textrm{UPowWP}\,}}(\mathcal {C})$ denotes the uniform power word problem for the class $\mathcal {C}$. Analogous results for the uniform compressed word problem are not known. Indeed, whether the uniform compressed word problem for RAAGs is solvable in polynomial time is posed as an open problem in [40].

Our result for the uniform power word problem for graph products implies that the uniform power word problem for RAAGs can be solved in polynomial time. We can apply this result to the knapsack problem for RAAGs. The knapsack problem is a classical optimization problem that originally has been formulated for the integers. Myasnikov et al. introduced the decision variant of the knapsack problem for an arbitrary finitely generated group G: Given $g_1, \dots , g_n, g \in G$, decide whether there are $x_1, \dots , x_n \in \mathbb {N}$ such that $g_1^{x_1} \cdots g_n^{x_n} = g$ holds in the group G [51], see also [19, 22, 34, 44] for further work. For many groups G one can show that, if such $x_1, \ldots , x_n \in \mathbb {N}$ exist, then there exist such numbers of size $2^{\text {poly}(N)}$, where N it the total length of all words representing the group elements $g_1, \dots , g_n, g$. This holds for instance for RAAGs. In this case, one nondeterministically guesses the binary encodings of numbers $x_1, \ldots , x_n$ and then verifies, using an algorithm for the power word problem, whether $g_1^{x_1} \cdots g_n^{x_n} g^{-1} = 1$ holds. In this way, it was shown in [44] that for every RAAG the knapsack problem belongs to $\textsf{NP}$ (using the fact that the compressed word problem and hence the power word problem for a fixed RAAG belongs to P). Moreover, if the commutation graph of the RAAG G contains an induced subgraph $C_4$ (cycle on 4 nodes) or $P_4$ (path on 4 nodes), then the knapsack problem for G is $\textsf{NP}$-complete [44]. However, membership of the uniform version of the knapsack problem for RAAGs in $\textsf{NP}$ remained open. Our polynomial time algorithm for the uniform power word problem for RAAGs yields the missing piece: the uniform knapsack problem for RAAGs is indeed $\textsf{NP}$-complete.

1.1 Related Work

Implicitly, (variants of) the power word problem have been studied long before. In the commutative setting, Ge [24] has shown that one can verify in polynomial time an identity $\alpha _1^{x_1} \alpha _2^{x_2}\cdots \alpha _n^{x_n} = 1$, where the $\alpha _i$ are elements of an algebraic number field and the $x_i$ are binary encoded integers.

In [27], Gurevich and Schupp present a polynomial time algorithm for a compressed form of the subgroup membership problem for a free group F where group elements are represented in the form $a_1^{x_1} a_2^{x_2}\cdots a_n^{x_n}$ with binary encoded integers $x_i$. The $a_i$ must be, however, standard generators of the free group F. This is the same input representation as in [52] (for nilpotent groups) and is more restrictive then our setting, where we allow powers of the form $w^x$ for w an arbitrary word over the group generators (on the other hand, Gurevich and Schupp consider the subgroup membership problem, which is more general than the word problem).

Recently, the power word problem has been investigated in [19]. In [19] it is shown that the power word problem for a wreath product of the form $G \wr \mathbb {Z}$ with G finitely generated nilpotent belongs to $\textsf{uTC} ^0$. Moreover, the power word problem for iterated wreath products of the form $\mathbb {Z}^r \wr (\mathbb {Z}^r \wr (\mathbb {Z}^r \cdots ))$ belongs to $\textsf{uTC} ^0$. By a famous embedding theorem of Magnus [47], it follows that the power word problem for a free solvable groups is in $\textsf{uTC} ^0$. Finally, in [45] Zetzsche and the first author of this work showed that the power word problem for a solvable Baumslag-Solitar group $\textsf{BS}(1,q)$ belongs to $\textsf{uTC} ^0$.

The present paper is a combination of the two conference papers [43] (by the first and third author) and [58] (by the second and third author). Here we also correct a mistake that occurred in [58]: there, our results on graph products were stated without the additional assumption that the base groups do not have elements of order two. While we strongly conjecture this result to be true, our proof only works with this additional assumption. The key lies in the proof of Lemma 51 (which corresponds to Lemma 15 in [58, 59]) – indeed, the only place where we need this additional assumption. We give more technical details in Remarks 44 and 52.

2 Preliminaries

For integers $a \le b$ we write [a, b] for the interval $\{x \in \mathbb {Z}a \le x \le b\}$. For an integer $z \in \mathbb {Z}$ let us define $\llbracket x \rrbracket = [0,x]$ if $x \ge 0$ and $\llbracket x \rrbracket = [x,0]$ if $x < 0$.

2.1 Words

An alphabet is a (finite or infinite) non-empty set $\Sigma$; an element $a \in \Sigma$ is called a letter. The free monoid over $\Sigma$ is denoted by $\Sigma ^*$; its elements are called words. The multiplication of the free monoid is concatenation of words. The identity element is the empty word 1.

Consider a word $w = a_1 \cdots a_n$ with $a_i \in \Sigma$. For $A \subseteq \Sigma$ we write $\left|w\right|_{A}$ for the number of $i \in [1,n]$ with $a_i \in A$ and we set $\vert w\vert = \vert w\vert _\Sigma$ (the length of w) and $|w|_a = |w|_{\{a\}}$ for $a \in \Sigma$. A word w has period k if $a_i= a_{i+k}$ for all i with $i,i+k \in [1,n]$.

2.2 Monoids

Let M be an arbitrary monoid. Later, we will consider finitely generated monoids M, where elements of M are described by words over an alphabet of monoid generators. To distinguish equality as words from equality as elements of M, we also write $x=_My$ (or $x=y$ in M) to indicate equality in M (as opposed to equality as words). Let $x =_M uvw$ for some $x, u, v, w \in M$. We say u is a prefix of x, v is a factor of x, and w is a suffix of x. We call u a proper prefix if $u \ne x$. Similarly, v is a proper factor if $v \ne x$ and w is a proper suffix if $w \ne x$.

An element $u\in M$ is primitive if $u\ne _M v^k$ for any $v \in M$ and $k >1$. Two elements $u, v \in M$ are transposed if there are $x, y \in M$ such that $u =_M xy$ and $v =_M yx$. We also say that v is a transposition of u. We call u and v conjugate if there is an element $t \in M$ such that $ut = tv$ (note that this is sometimes called left-conjugate in the literature). For a free monoid $\Sigma ^*$, two words u, v are transposed if and only if they are conjugate. In this case, we also say that the word u is a cyclic permutation of the word v.

2.3 Rewriting Systems over Monoids

A rewriting system over the monoid M is a subset $S \subseteq M \times M$. We write $\ell \rightarrow r$ if $(\ell , r) \in S$. The corresponding rewriting relation $\underset{S}{\Longrightarrow }$ over M is defined by: $u \underset{S}{\Longrightarrow }\ v$ if and only if there exist $\ell \rightarrow r\in S$ and $s,t \in M$ such that $u =_M s\ell t$ and $v =_M sr t$. We also say that u can be rewritten to v in one step. Let $\overset{+}{\underset{S}{\Longrightarrow }}$ be the transitive closure of $\underset{S}{\Longrightarrow }$ and $\overset{*}{\underset{S}{\Longrightarrow }}$ the reflexive and transitive closure of $\overset{S}{\Longrightarrow }$. We write $u \overset{\le k}{\underset{S}{\Longrightarrow }} v$ (resp. $u \overset{K}{\underset{S}{\Longrightarrow }} v$) to denote that u can be rewritten to v using at most (resp. exactly) k steps. We say that $w \in M$ is irreducible with respect to S if there is no $v \in M$ with $w \underset{S}{\Longrightarrow }\ v$. The set of irreducible monoid elements is denoted as ${{\,\textrm{IRR}\,}}(S) = \left\{ w \in M \mid w \text { is irreducible} \right\}$. A rewriting system S is called confluent if, whenever $x\overset{*}{\underset{S}{\Longrightarrow }}y$ and $x\overset{*}{\underset{S}{\Longrightarrow }}z$, then there is some w with $y\overset{*}{\underset{S}{\Longrightarrow }}w$ and $z\overset{*}{\underset{S}{\Longrightarrow }}w$. Note that if S is confluent, then for each v there is at most one $w \in {{\,\textrm{IRR}\,}}(S)$ with $v\overset{*}{\underset{S}{\Longrightarrow }}w$. A rewriting system S is called terminating if there is no infinite chain

$$\begin{aligned} x_0 \underset{S}{\Longrightarrow }\ x_1 \underset{S}{\Longrightarrow }\ \cdots x_{i-1} \underset{S}{\Longrightarrow }\ x_i \underset{S}{\Longrightarrow }\ \cdots . \end{aligned}$$

We write M/S for the quotient monoid $M/\equiv _S$, where $\equiv _S$ is the smallest congruence relation on M that contains S.

The above notion of a rewriting system over a monoid M is a generalization of the notion of a string rewriting system, which is a rewriting system over a free monoid $\Sigma ^*$. For further details on rewriting systems we refer to [10, 32].

2.4 Partially Commutative Monoids

In this subsection, we introduce a few basic notations concerning partially commutative monoids. More information can be found in [14].

Let $\Sigma$ be an alphabet of symbols. We do not require $\Sigma$ to be finite. Let $I \subseteq \Sigma \times \Sigma$ be a symmetric and irreflexive relation. The partially commutative monoid defined by $(\Sigma , I)$ is the quotient monoid

$$\begin{aligned} M(\Sigma , I) = \Sigma ^*/\{(ab,ba)\mid (a,b)\in I\}. \end{aligned}$$

Thus, the relation I describes which generators commute; it is called the commutation relation or independence relation. The relation $D = (\Sigma \times \Sigma ) \setminus I$ is called dependence relation and $(\Sigma , D)$ is called a dependence graph. The monoid $M(\Sigma , I)$ is also called a trace monoid and its elements are called traces or partially commutative words. Note that for words $u,v \in \Sigma ^*$ with $u =_{M(\Sigma , I)} v$ we have $\left| u\right| _a=\left| v\right| _a$ for every $a \in \Sigma$. Hence, the length $\left| w\right|$ and $\left| w\right| _a$ for a trace $w \in M(\Sigma , I)$ is well-defined and we use this notation henceforth.

A letter a is called a minimal letter of $w \in M(\Sigma ,I)$ if $w =_{M(\Sigma , I)} au$ for some $u\in M(\Sigma ,I)$. Likewise a letter a is called a maximal letter of w if $w =_{M(\Sigma , I)} ua$ for some $u\in M(\Sigma ,I)$. When we say that a is minimal (maximal) in $w \in \Sigma ^*$, we mean that a is minimal (maximal) in the trace represented by w. Note that if both a and $b \ne a$ are minimal (maximal) letters of w, then $(a,b) \in I$. A trace rewriting system is simply a rewriting system over a trace monoid $M(\Sigma , I)$ in the sense of Section 2.3. If $\Delta \subseteq \Sigma$ is a subset, we write $M(\Delta , I)$ for the submonoid of $M(\Sigma , I)$ generated by $\Delta$.

Be aware of the ambiguity between the dependence graph $(\Sigma , D)$ describing which generators commute, and the dependence graph of a trace w as described in the following.

Elements of a partially commutative monoid can be represented by node-labelled directed acyclic graphs: Let $w = a_1 \cdots a_n$ with $a_i \in \Sigma$. We define the dependence graph of w as follows: The node set is [1, n], node i is labelled with $a_i$ and there is an edge $i \rightarrow j$ if and only if $i < j$ and $(a_i, a_j) \in D$. Then, for two words $u,v \in \Sigma ^*$ we have $u =_{M(\Sigma ,I)} v$ if and only if the dependence graphs of u and v are isomorphic (as node-labelled directed graphs). The dependence graph of a trace $v \in M(\Sigma , I)$ is the dependence graph of (any) word representing v. The trace v is said to be connected if its dependence graph is weakly connected (i.e., connected if we forget the direction of edges), or, equivalently, if the induced subgraph of $(\Sigma ,D)$ consisting only of the letters occurring in v is connected. The connected components of the trace v are the weakly connected components of the dependence graph of v.

2.4.1 Levi’s Lemma

As a consequence of the representation of traces by dependence graphs, one obtains Levi’s lemma for traces (see e.g. [14, p. 74]), which is one of the fundamental facts in trace theory. The formal statement is as follows.

Lemma 1

(Levi’s lemma) Let $M = M(\Sigma ,I)$ be a trace monoid and $u_1, \ldots , u_m, v_1,$ $\ldots , v_n \in M$. Then

$$\begin{aligned} u_1u_2 \cdots u_m =_M v_1 v_2 \cdots v_n \end{aligned}$$

if and only if there exist $w_{i,j} \in M(\Sigma ,I)$ (for $i \in [1,m]$, $j \in [1,n]$) such that

• $u_i =_M w_{i,1}w_{i,2}\cdots w_{i,n}$ for every $i \in [1,m]$,

• $v_j =_M w_{1,j}w_{2,j}\cdots w_{m,j}$ for every $j \in [1,n]$, and

• $(w_{i,j}, w_{k,\ell }) \in I$ if $1 \le i < k \le m$ and $n \ge j > \ell \ge 1$.

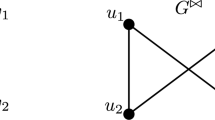
The situation in the lemma will be visualized by a diagram of the following kind. The i–th column corresponds to $u_i$, the j–th row (read from bottom to top) corresponds to $v_j$, and the intersection of the i–th column and the j–th row represents $w_{i,j}$. Furthermore, $w_{i,j}$ and $w_{k,\ell }$ are independent if one of them is left-above the other one. So, for instance, all $w_{i,j}$ in the red part are independent from all $w_{k,\ell }$ in the blue part.

Usually, Levi’s lemma is formulated for the case that the alphabet $\Sigma$ is finite. But the case that $\Sigma$ is finite already implies the general case with $\Sigma$ possibly infinite: simply replace the trace monoid $M(\Sigma ,I)$ by $M(\Sigma ',I')$, where $\Sigma '$ contains all symbols occurring in one of the traces $u_i, v_j$ and $I'$ is the restriction of I to $\Sigma '$.

A consequence of Levi’s Lemma is that trace monoids are cancellative, i.e., $usv=utv$ implies $s=t$ for all traces $s,t,u,v\in M$.

2.4.2 Projections to Free Monoids

It is a well-known result [17, 18, 62] that every trace monoid can be embedded into a direct product of free monoids. In this section we recall the corresponding results.

Consider a trace monoid $M = M(\Sigma , I)$ with the property that there exist finitely many sets $A_i \subseteq \Sigma$ ($i \in [1,k]$ for some $k\in \mathbb {N}$) fulfilling the following property:

$$\begin{aligned} (a, b) \in D \text { if and only if } \exists i \in [1,k] : a,b \in A_i. \end{aligned}$$

Since D is reflexive this implies that for every $a\in \Sigma$ there is an i such that $a\in A_i$. property if one takes for the $A_i$ the maximal cliques in the dependence graph $(\Sigma ,D)$ [18]. If $\Sigma$ is finite, one can take for the $A_i$ also all sets $\{a, b\}$ with $(a, b) \in D$ together with all singletons $\{a\}$ with a an isolated vertex in $(\Sigma ,D)$ [17].

Let $\pi _i:\Sigma ^* \rightarrow A_i^*$ be the projection to the free monoid $A_i^*$ defined by $\pi _i(a) = a$ for $a \in A_i$ and $\pi _i(a) = 1$ otherwise. We define a projection $\Pi :\Sigma ^* \rightarrow A_1^*\times \cdots \times A_k^*$ to a direct product of free monoids by $\Pi (w) = (\pi _1(w), \dots , \pi _k(w))$. It is straightforward to see that, if $u =_M v$, then also $\Pi (u) = \Pi (v)$. Hence, we can consider $\Pi$ also as a monoid morphism $\Pi :M \rightarrow A_1^*\times \cdots \times A_k^*$ (which from now on we denote by the same letter $\Pi$). We will make use of the following two lemmata presented in [18].

Lemma 2

([62, Lemma 1], [18, Proposition 1.2]) Let $M = M(\Sigma , I)$. For $u, v \in \Sigma ^*$ we have $u =_M v$ if and only if $\Pi (u) = \Pi (v)$.

Thus, $\Pi$ is an injective monoid morphism $\Pi :M \rightarrow A_1^*\times \cdots \times A_k^*$.

Lemma 3

[18, Proposition 1.7]) Let $M = M(\Sigma , I)$, $w \in \Sigma ^*$ and $t > 1$. Then, there is $u \in \Sigma ^*$ with $w =_M u^t$ if and only if there is a tuple $\textbf{v} \in \prod _{i=1}^k A_i^*$ with $\Pi (w) = \textbf{v}^t$.

In [18] these lemmata are only proved for the case that $\Sigma$ is finite, but as for Levi’s Lemma one obtains the general case by restricting $(\Sigma ,I)$ to those letters that appear in the traces involved.

Projections onto free monoids were used in [18] in order to show the following lemmata.

Lemma 4

([18, Corollary 3.13]) Let $M = M(\Sigma , I)$ and $u,v \in M$. Then there is some $x \in M$ with $xu =_M vx$ if and only if u and v are related by a sequence of transpositions, i. e., there are $y_1, \dots , y_k$ such that $u = y_1$, $v = y_k$ and $y_{i+1}$ is a transposition of $y_i$.

Lemma 4 gives us a tool for checking conjugacy in $M(\Sigma , I)$; indeed, from now on, we will most of the time use that conjugate elements are related by a sequence of transpositions.

Lemma 5

([18, Proposition 3.5]) Let $M = M(\Sigma , I)$ and $u,v,p,q \in M$ such that $u = p^k$ and $v = q^\ell$ with p and q primitive and $k,\ell \ge 1$. Then u and v are conjugate if and only if $k = \ell$ and p and q are conjugate.

Note that Lemma 5 implies that if u is conjugate to a primitive trace, then u must be primitive as well.

2.5 Trace Monoids Defined by Finite Graphs

As a first step towards graph products let us introduce the following notation for trace monoids: Let $\mathcal {L}$ be a finite set of size $\sigma = |\mathcal {L}|$ and $I \subseteq \mathcal {L}\times \mathcal {L}$ be irreflexive and symmetric (i. e., $(\mathcal {L},I)$ is a finite undirected simple graph). Moreover, assume that for each $\zeta \in \mathcal {L}$ we are given a (possibly infinite) alphabet $\Gamma _\zeta$ such that $\Gamma _\zeta \cap \Gamma _\xi = \emptyset$ for $\zeta \ne \xi$. By setting $\Gamma = \bigcup _{\zeta \in \mathcal {L}}\Gamma _\zeta$ and $I_\Gamma = \{(a,b) (\zeta ,\xi ) \in I, a\in \Gamma _\zeta , b\in \Gamma _\xi \}$, we obtain a trace monoid $M = M(\Gamma , I_\Gamma )$. Henceforth, we simply write I for $I_\Gamma$. For $a \in \Gamma$ we define ${{\,\textrm{alph}\,}}(a) = \zeta$ if $a \in \Gamma _\zeta$. For $u= a_1\cdots a_k \in \Gamma ^*$ we define ${{\,\textrm{alph}\,}}(u) = \{{{\,\textrm{alph}\,}}(a_1), \dots , {{\,\textrm{alph}\,}}(a_k)\}$.

The following lemma characterizes the shape of a prefix, suffix or factor of a power in the above trace monoid M.

Lemma 6

Let $p \in M$ be connected and $k \in \mathbb {N}$. Then we have:

• 1. If $p^k =_M uw$ for traces $u,w \in M(\Gamma , I)$, then there exist $s < \sigma$, $\ell ,m \in \mathbb {N}$ and factorizations $p = u_i w_i$ for $i \in [1,s]$ such that

  • $k = \ell +s+m$,

  • $u_i \ne 1 \ne w_i$ for all $i \in [1,s]$ and $(w_i,u_j) \in I$ for $i < j$,

  • $u =_M p^{\ell }u_1\cdots u_s$ and $w =_M w_1\cdots w_s p^m$.

• 2. Given a factor v of $p^k$ at least one of the following is true.

  • $v = u_1\cdots u_a v_1 \cdots v_b w_1 \cdots w_c$ where $a, b, c \in \mathbb {N}$, $a + b + c \le 2\sigma - 2$, $u_i$ is a proper suffix of p for $i \in [1,a]$, $v_i$ is a proper factor of p for $i \in [1,b]$ and $w_i$ is a proper prefix of p for $i \in [1,c]$.

  • $v = u_1\cdots u_a p^b w_1 \cdots w_c$ where $a, b, c \in \mathbb {N}$, $a, c < \sigma$, $u_i$ is a proper suffix of p for $i \in [1,a]$ and $w_i$ is a proper prefix of p for $i \in [1,c]$.

Figure 1 illustrates case (i) of Lemma 6.

Fig. 1

A factorization of $p^k$ as in case 1 of Lemma 6

Proof

Let us start with the first statement. We apply Levi’s Lemma to the identity $p^k =_M uw$ and obtain the following diagram:

We have $(w_i, u_{i+1}) \in I$ and hence ${{\,\textrm{alph}\,}}(w_i) \cap {{\,\textrm{alph}\,}}(u_{i+1}) = \emptyset$ for all $i \in [1,k-1]$. Since ${{\,\textrm{alph}\,}}(p) = {{\,\textrm{alph}\,}}(u_j) \cup {{\,\textrm{alph}\,}}(w_j)$ for all $j \in [1,k]$, this implies ${{\,\textrm{alph}\,}}(u_{i+1}) \subseteq {{\,\textrm{alph}\,}}(u_i)$. Now assume that $i \in [1,k-1]$ is such that $u_i \ne 1 \ne w_i$. We have $(u_{i+1}, w_i) \in I$. Since we cannot have $(u_i, w_i) \in I$ (p is connected), we cannot have ${{\,\textrm{alph}\,}}(u_i) \subseteq {{\,\textrm{alph}\,}}(u_{i+1})$. Therefore, ${{\,\textrm{alph}\,}}(u_{i+1}) \subsetneq {{\,\textrm{alph}\,}}(u_{i})$ whenever $u_i \ne 1 \ne w_i$. It follows that there are $\ell ,m \ge 0$ and $s < \sigma$ such that $k = \ell +s+m$ and

• $u_i = p$, $w_i = 1$ for $i \in [1,x]$,

• $u_i \ne 1 \ne w_i$, $u_i w_i = p$ for $i \in [x+1,x+s]$, and

• $u_i = 1$, $w_i = p$ for $i \in [x+s+1,k]$.

By renaming $u_{x+i}$ and $w_{x+i}$ into $u_i$ and $w_i$, respectively, for $i \in [1,s]$ we obtain factorizations $u =_M p^\ell u_1 \cdots u_s$ and $w =_M w_1 \cdots w_s p^m$ for some $s < \sigma$ and traces $u_i, w_i \in M\setminus \{1\}$ with $p =_M u_i w_i$. This yields statement 1.

To derive statement 2, consider the factorization $p^k =_M u (vw)$. Applying the final conclusion of the previous paragraph, we obtain factorizations $u =_M p^x u_1 \cdots u_s$ and $vw =_M x_1 \cdots x_s p^\ell$ where $s < \sigma$, the $u_i$ are proper prefixes of p, the $x_i$ are proper suffixes of p and $k = x + s + \ell$.

We then consider two cases: if $\ell = 0$, then $vw =_M x_1 \cdots x_s$. Applying Levi’s Lemma to this factorization yields the following diagram:

Hence, $v =_M v_1 v_2 \cdots v_s$, where every $v_i$ is a prefix of the proper suffix $x_i$ of p. Therefore, $v_i$ is a proper factor of p.

Now assume that $\ell > 0$. Applying Levi’s Lemma to $vw =_M x_1 \cdots x_s p^\ell$ yields a diagram of the following form:

To the factorizations $p =_M v_{s+i} w_{s+i}$ ($i \in [1,\ell ]$) we apply the arguments used for the proof of statements 1 and 2. There are $y,z \ge 0$ and $t < \sigma$ such that $\ell = y+t+z$ and

• $v_{s+i} = p$, $w_{s+i} = 1$ for $i \in [1,y]$,

• $v_{s+i} \ne 1 \ne w_{s+i}$, $v_{s+i} w_{s+i} =_M p$ for $i \in [y+1,y+t]$, and

• $v_{s+i} = 1$, $w_{s+i} = p$ for $i \in [y+t+1,\ell ]$.

We obtain $v =_M v_1 \cdots v_s p^y v_{s+y+1} \cdots v_{s+y+t}$ where every $v_{s+y+i}$ ($i \in [1,t]$) is a proper prefix of p. If $y > 0$ then $(v_{s+1}, w_1 \cdots w_s) \in I$ implies $w_1 \cdots w_s = 1$. Hence, every $v_i$ ($i \in [1,s]$) is proper suffix of p (by a symmetric argument, we could write v also as a concatenation of $s < \sigma$ many proper suffixes of p followed by $t < \sigma$ many proper factors of p).

Finally, assume that $y=0$. We get $v =_M v_1 \cdots v_s v_{s+y+1} \cdots v_{s+y+t}$ with every $v_i$ ($i \in [1,s]$) a proper factor of p and every $v_{s+y+i}$ ($i \in [1,t]$) a proper prefix of p. $\square$

For a trace $u\in M = M(\Gamma ,I)$ and $\zeta \in \mathcal {L}$, we write $\left| u\right| _\zeta = \left| u\right| _{\Gamma _\zeta } = \sum _{a\in \Gamma _\zeta } \left| u\right| _a$. Note that, while the sum might be infinite, only finitely many summands are non-zero.

Lemma 7

Let $r,s,t,u\in M$ with $rs =_M tu$ and, for all $\zeta \in \mathcal {L}$, $\left| s\right| _\zeta \ge \left| u\right| _\zeta$ or, equivalently, $\left| r\right| _\zeta \le \left| t\right| _\zeta$. Then, as elements of M, u is a suffix of s and r is a prefix of t. In particular, if for all $\zeta \in \mathcal {L}$ we have $\left| s\right| _\zeta = \left| u\right| _\zeta$, then $s =_M u$ and $r =_M t$.

Proof

By Levi’s Lemma, there are $p,q,x,y \in M$ with $(x,y) \in I$ and $r=px$, $t = py$, $s =yq$, and $u = xq$. Because of the condition $\left| s\right| _\zeta \ge \left| u\right| _\zeta$ for all $\zeta \in \mathcal {L}$, x must be the empty trace.

The second part of the lemma follows by using the first part for the two inequalities $\left| s\right| _\zeta \ge \left| u\right| _\zeta$ and $\left| u\right| _\zeta \ge \left| s\right| _\zeta$. $\square$

Lemma 8

Let $p^\sigma u=_Mvp^\sigma$ (where $\sigma = |\mathcal {L}|$ as above) for some primitive and connected trace p and let $u \in M$ be a prefix of $p^k$ for some $k\in \mathbb {N}$. Then we have $u=v=p^\ell$ for some $\ell \in [0,k]$.

Proof

If u is the empty prefix, we are done. Hence, from now on, we can assume that u is non-empty. First consider the case that p is a prefix of u. Then, $p^{\sigma +1}$ is a prefix of $vp^\sigma$. Hence, there is a trace q with $vp^\sigma =_M pq$, where $p^\sigma$ is a factor of q. Then Lemma 7 implies that p is a prefix of v.

If $v =_M pv'$ and $u =_M p u'$, we obtain $p^{\sigma +1} u' =_M p v' p^{\sigma }$. Cancelling p yields $p^\sigma u' =_M v' p^\sigma$. Since $u'$ is a prefix of $p^{k-1}$ we can replace u and v by $u'$ and $v'$, respectively. Therefore, we can assume that p is not a prefix of u. Since u is a prefix of some $p^k$, Lemma 6 implies that u is already a prefix of $p^\sigma$.

Let us next show that $u=v$. To do so, we write $p^\sigma =_M uw$. Then we have

$$\begin{aligned} uwu =_M p^\sigma u =_M vp^\sigma =_M vuw. \end{aligned}$$

Since $\left| wu\right| _a = \left| uw \right| _a$ for all $a \in \Gamma$, Lemma 7 implies $u=v$.

Now, we have $p^\sigma u=_Mup^\sigma$. Since p is connected, [17, Proposition 3.1] implies that there are $i,j \in \mathbb {N}$ with $p^{\sigma \cdot i} =_M u^j$. Then, by [17, Theorem 1.5] it follows that there are $t \in M$ and $\ell ,m \in \mathbb {N}$ with $p=_Mt^m$ and $u=_Mt^\ell$. As p is primitive, we have $m = 1$ and $t=p$ and hence $u =_M = p^\ell$. Since u is a prefix of $p^k$, we have $\ell \le k$. $\square$

To prove the next lemma, we want to apply Lemma 2. To do so, we use the following projections suitable for our use case. Let

$$\begin{aligned} \mathcal {A} = \left\{ \Gamma _\zeta \cup \Gamma _\xi \mid (\zeta , \xi ) \in D, \zeta \ne \xi \right\} \cup \{ \Gamma _\zeta \mid \zeta \text { is isolated} \}, \end{aligned}$$

(1)

where $\zeta$ is isolated if there is no $\xi \ne \zeta$ with $(\zeta , \xi ) \in D$ (and $D= \mathcal {L}\times \mathcal {L}\setminus I$). Notice that even though $\Gamma$ might be infinite, $\mathcal {A}$ is finite in any case (because $\mathcal {L}$ is finite). Let us write $\mathcal {A}=\{A_1, \ldots , A_k\}$ and $\pi _i$ for the projection $M(\Gamma ,I) \rightarrow A_i^*$.

Lemma 9

Let $u,v,p,q \in M$ and $k\in \mathbb {N}$ with $uqv =_M p^k$ and $\left| p \right| _\zeta = \left| q \right| _\zeta$ for all $\zeta \in \mathcal {L}$. Then p and q are conjugate in M.

Proof

First, we are going to show that the transposition qvu of uqv is equal to $q^k$ in M. Consider the projections $\pi _i$ onto $A_i$ from above. By the assumption $\left| p \right| _\zeta = \left| q \right| _\zeta$ for all $\zeta \in \mathcal {L}$, it follows that $\left| \pi _i(p)\right| = \left| \pi _i(q)\right|$. As $\pi _i(p^k)$ has a period $\left| \pi _i(p)\right|$, so has its cyclic permutation $\pi _i(qvu)$. As its first $\left| \pi _i(p)\right|$ letters are exactly $\pi _i(q)$, it follows that $\pi _i(qvu) = \pi _i(q^k)$. Since this holds for all i, it follows by Lemma 2 that $qvu =_M q^k$.

Now, observe that $q^k =_M qvu$ and $p^k =_M uqv$ are conjugate in M. Hence, it remains to apply Lemma 5 to conclude that p and q are conjugate: we write $p=\tilde{p}^i$ and $q=\tilde{q}^j$ for primitive traces $\tilde{p}, \tilde{q}$. Then Lemma 5 tells us that $i=j$ and $\tilde{p}$ and $\tilde{q}$ are conjugate. Hence, also p and q are conjugate. $\square$

2.6 Groups

If G is a group, then $u, v \in G$ are conjugate if and only if there is a $g \in G$ such that $u =_G g^{-1}vg$ (note that this agrees with the above definition for monoids).

2.6.1 Free Groups

Let X be a set and $\overline{X} = \{\overline{a }~\vert ~a \in X\}$ be a disjoint copy of X. We extend the mapping $a \mapsto \overline{a}$ to an involution without fixed points on $\Sigma = X \cup \overline{X}$ by $\overline{\overline{a}} = a$ and finally to an involution on $\Sigma ^*$ by $\overline{a_1 a_2 \cdots a_n} = \overline{a_n} \cdots \overline{a_2} \;\overline{a_1}$. The only fixed point of the latter involution is the empty word 1. The string rewriting system

$$\begin{aligned} S_{\textrm{free}}= \{a \overline{a} \rightarrow 1~|~ a \in \Sigma \} \end{aligned}$$

is strongly confluent and terminating meaning that for every word $w \in \Sigma ^*$ there exists a unique word $\hat{w} \in {{\,\textrm{IRR}\,}}(S_{\textrm{free}})$ with $w \overset{*}{\underset{S_{\textrm{free}}}{\Longrightarrow }} \hat{w}$. Words from ${{\,\textrm{IRR}\,}}(S_{\textrm{free}})$ are called freely reduced. The system $S_{\textrm{free}}$ defines the free group $F(X) = \Sigma ^*/ S_{\textrm{free}}$ with basis X. Let $\eta :\Sigma ^* \rightarrow F(X)$ denote the canonical monoid homomorphism. Then we have $\eta (w)^{-1} = \eta (\overline{w})$ for all words $w \in \Sigma ^*$. If $|X|=2$, then we write $F_2$ for F(X). It is known that for every countable set X, $F_2$ contains an isomorphic copy of F(X).

2.6.2 Finitely Generated Groups and the Word Problem

A group G is called finitely generated (f.g.) if there exists a finite set X and a surjective group homomorphism $h :F(X) \rightarrow G$. In this situation, the set $\Sigma = X \cup \overline{X}$ is called a finite (symmetric) generating set for G. Usually, we write $X^{-1}$ instead of $\overline{X}$ and $a^{-1}$ instead of $\overline{a}$ for $a \in \Sigma$. Thus, for an integer $z < 0$ and $w \in \Sigma ^*$ we write $w^z$ for $(\overline{w})^{-z}$.

In many cases we can think of $\Sigma$ as a subset of G, but, in general, we can also have more than one letter for the same group element. The group identity of G is denoted with 1 as well (this fits to our notation 1 for the empty word which is the identity of F(X)).

For words $u,v \in \Sigma ^*$ we usually say that $u = v$ in G or $u =_G v$ in case $h(\eta (u)) = h(\eta (v))$ and we do not write $\eta$ nor h from now on. The word problem for the finitely generated group G, $\text {WP}(G)$ for short, is defined as follows:

$\textsf {Input}$:

a word $w \in \Sigma ^*$.

$\textsf {Output}$:

Does $w=_G 1$ hold?

2.6.3 The Power Word Problem

A power word (over $\Sigma$) is a tuple $(u_1,x_1,u_2,x_2,\ldots ,u_n,x_n)$ where $u_1, \dots , u_n \in \Sigma ^*$ are words over the group generators and $x_1, \dots , x_n\in \mathbb {Z}$ are integers that are given in binary notation. Such a power word represents the word $u_1^{x_1} u_2^{x_2}\cdots u_n^{x_n}$. Quite often, we will identify the power word $(u_1,x_1,u_2,x_2,\ldots ,u_n,x_n)$ with the word $u_1^{x_1} u_2^{x_2}\cdots u_n^{x_n}$. Moreover, if $x_i=1$, then we usually omit the exponent 1 in a power word. The power word problem for the finitely generated group G, ${{\,\textrm{PowWP}\,}}(G)$ for short, is defined as follows:

$\textsf {Input}$:

a power word $(u_1,x_1,u_2,x_2,\ldots ,u_n,x_n)$.

$\textsf {Output}$:

Does $u_1^{x_1} u_2^{x_2}\cdots u_n^{x_n}=_G 1$ hold?

Due to the binary encoded exponents, a power word can be seen as a succinct description of an ordinary word. Hence, a priori, the power word problem for a group G could be computationally more difficult than the word problem. An example, where this happens (under standard assumptions from complexity theory) is the wreath product $S_5 \wr \mathbb {Z}$ (where $S_5$ is the symmetric group on 5 elements). The word problem for this group can be easily solved in logspace, whereas the power word problem for $S_5 \wr \mathbb {Z}$ is $\textsf{coNP}$-complete [43].

Let $\mathcal {C}$ be a countable class of groups, where every group has a finite description. We also assume that the description of $G \in \mathcal {C}$ contains a generating set for G. We write ${{\,\textrm{UPowWP}\,}}(\mathcal {C})$ for the uniform power word problem:

$\textsf {Input}$:

a group $G \in \mathcal {C}$ and a power word $(u_1,x_1,u_2,x_2,\ldots ,u_n,x_n)$ over the generating set of G.

$\textsf {Output}$:

Does $u_1^{x_1} u_2^{x_2}\cdots u_n^{x_n}=_G 1$ hold?

2.6.4 Right-angled Artin Groups

Right-angled Artin groups are defined similarly to partially commutative monoids. Again we have a symmetric and irreflexive commutation relation $I \subseteq X \times X$. Note that we have $M(X,I) \subseteq G(X,I)$.

We can view G(X, I) also as follows: let $\Sigma = X \cup \overline{X}$ where $\overline{X}$ is a disjoint copy of X and $\overline{\overline{a}} = a$ for $a \in \Sigma$ (like for free groups). Extend I to a symmetric relation on $\Sigma$ by requiring that $(a, b) \in I$ if and only if $(\overline{a}, b) \in I$ for $a,b \in \Sigma$. Then G(X, I) is the quotient of $M(\Sigma ,I)$ defined by the relations $a\overline{a}=1$ for $a \in \Sigma$. A trace $w \in M(\Sigma ,I)$ is called reduced if it does not contain a factor $a\overline{a}$ for $a \in \Sigma$. For every trace $u \in M(\Sigma ,I)$ there is a unique reduced trace v (the reduced normal form of u) with $u = v$ in G(X, I). Like for free groups, it can be computed using the confluent and terminating trace rewriting system $\{ a \overline{a} \rightarrow 1 \mid a \in \Sigma \}$.

2.6.5 Graph Products

Let $\left( G_\zeta \right) _{\zeta \in \mathcal {L}}$ be a family of so-called base groups and $I \subseteq \mathcal {L}\times \mathcal {L}$ be an irreflexive and symmetric relation (the independence relation). As before, we assume that $\mathcal {L}$ is always finite and we write $\sigma = \left| \mathcal {L}\right|$. The graph product ${{\,\textrm{GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}})$ is defined as the free product of the $G_\zeta$ modulo the relations expressing that elements from $G_\zeta$ and $G_\xi$ commute whenever $(\zeta ,\xi ) \in I$. Below, we define this group by a group presentation.

Let $\Gamma _\zeta = G_\zeta \setminus \{ 1 \}$ be the set of non-trivial elements of the group $G_\zeta$ for $\zeta \in \mathcal {L}$. We assume w.l.o.g. that the sets $\Gamma _\zeta$ are pairwise disjoint. We then define $\Gamma$ and $I_{\Gamma }$ as in Section 2.5: $\Gamma = \bigcup _{\zeta \in \mathcal {L}} \Gamma _\zeta$ (note that typically, $\Gamma$ will be infinite) and $I_\Gamma = \{ (a, b) \in \Gamma \times \Gamma \mid ({{\,\textrm{alph}\,}}(a), {{\,\textrm{alph}\,}}(b)) \in I\}$. As in Section 2.5 we write I instead of $I_\Gamma$. For $a,b \in G_\zeta$ we write [ab] for the element of $G_\zeta$ obtained by multiplying ab in $G_{\zeta }$ (whereas ab denotes a two-letter word in $\Gamma ^*$). Here, we identify $1\in G_\zeta$ with the empty word 1. The relation I is extended to $\Gamma ^*$ by $I = \{ (u,v) \in \Gamma ^* \times \Gamma ^* \mid {{\,\textrm{alph}\,}}(u) \times {{\,\textrm{alph}\,}}(v) \subseteq I \}$ (where ${{\,\textrm{alph}\,}}(u) \subseteq \mathcal {L}$ is defined as in Section 2.5). With these definitions we have

$$\begin{aligned} {{\,\text {GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}}) = \left\langle \, { \Gamma }\; |\; { ab = [ab] \text{ for } \zeta \in \mathcal {L}, a,b\in \Gamma _\zeta , ab = ba \text{ for } (a,b)\in I} \, \right\rangle \! . \end{aligned}$$

Example 10

If $I = \emptyset$, then ${{\,\textrm{GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}})$ is simply the free product $*_{\zeta \in \mathcal {L}} \, G_\zeta$.

Example 11

If all the base groups are the infinite cyclic group (i. e., for each $\zeta \in \mathcal {L}$ we have $G_\zeta = \mathbb {Z}$), then the graph product ${{\,\textrm{GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}})$ is the RAAG $G(\mathcal {L}, I)$.

Let $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}})$ be a graph product and $M = M(\Gamma , I)$ the corresponding trace monoid (see Section 2.4). Notice that M satisfies the setting of Section 2.5 – so these results and definitions apply to the case of graph products. We can represent elements of G by elements of M. More precisely, there is a canonical surjective homomorphism $h :M \rightarrow G$. A reduced representative of a group element $g \in G$ is a trace w of minimal length such that $h(w) = g$. We also say that w is reduced. Equivalently, $w \in M$ is reduced if there is no two-letter factor ab of w such that ${{\,\textrm{alph}\,}}(a) = {{\,\textrm{alph}\,}}(b)$. A trace $w \in M$ is called cyclically reduced if all transpositions of w are reduced. Equivalently, w is cyclically reduced if it is reduced and it cannot be written in the form axb with $a,b \in \Gamma _\zeta$ for some $x \in M$. Note that this definition agrees with [33], whereas in [19] a slightly different definition is used. We call a trace $w \in M$ composite if $\left| {{\,\textrm{alph}\,}}(w)\right| \ge 2$. Notice that a trace w, where every connected component is composite, is cyclically reduced if and only if ww is reduced (then, every $w^k$ with $k \ge 2$ is reduced). A word $w \in \Gamma ^*$ is called reduced/cyclically reduced/composite if the trace represented by w is reduced/cyclically reduced/composite.

Remark 12

Note that a word $w \in \Gamma ^*$ is cyclically reduced if and only if every cyclic permutation of the word w is reduced as a trace (be aware of the subtle difference between a cyclic permutation of a word w and a transposition of the trace represented by w): If the trace represented by w is cyclically reduced, then clearly every cyclic permutation of w must be reduced. On the other hand, assume that $w =_M a w' b$ with $a,b \in \Gamma _\zeta$. Then we can write the word w as $w = x a y b z$ such that $(a, xz) \in I$. Then ybzxa is a cyclic permutation of w that is not reduced.

On the free monoid $\Gamma ^*$ we can define an involution $(\cdot )^{-1}$ by $(a_1 a_2 \cdots a_n)^{-1} = a_n^{-1} \cdots a_2^{-1} a_1^{-1}$, where $a_i^{-1}$ is the inverse of $a_i$ in the group $G_{{{\,\textrm{alph}\,}}(a_i)}$. Note that $u =_M v$ implies $u^{-1} =_M v^{-1}$. Therefore, we obtain a well-defined involution $(\cdot )^{-1}$ on M. Moreover, $u^{-1}$ indeed represents the inverse of u in the group G.

The counterpart of the rewriting system $S_{\textrm{free}}$ for graph products is the trace rewriting system

$$\begin{aligned} T= \{ a b \rightarrow [ab]~\big \vert ~a,b \in \Gamma , {{\,\textrm{alph}\,}}(a) = {{\,\textrm{alph}\,}}(b)\}. \end{aligned}$$

(2)

Note that $G = M / T$ and that ${{\,\textrm{IRR}\,}}(T)$ is the set of reduced traces. Moreover, T is terminating and confluent; the latter is shown in [36, Lemma 6.1]. The following lemma can be found in [28, Lemma 24].

Lemma 13

Let $u, v \in \Gamma ^*$. If $u =_M v$, then also $u =_G v$. Moreover, if u and v are reduced, then $u =_M v$ if and only if $u =_G v$.

The following commutative diagram summarizes the mappings between the sets introduced in this section ($\hookrightarrow \hspace{-8pt}\rightarrow$ indicates a bijection):

(3)

The embedding $M(\Gamma ,I)\hookrightarrow G(\Gamma ,I)$ is induced by the embedding $M(\Gamma ,I)\hookrightarrow M(\Gamma \cup \overline{\Gamma },I)$ composed with the projection $M(\Gamma \cup \overline{\Gamma },I) \twoheadrightarrow G(\Gamma ,I)$ from Section 2.6.4.

Note that, in the trace monoid $M(\Gamma \cup \overline{\Gamma },I)$ for every symbol $a \in \Gamma$ there is a formal inverse $\overline{a}$ such that $(\overline{a},b) \in I$ if and only if $(a,b) \in I$. This formal inverse $\overline{a}$ is different from the inverse of a in base group $G_{{{\,\textrm{alph}\,}}(a)}$, but the surjection $G(\Gamma ,I) \twoheadrightarrow {{\,\textrm{GP}\,}}(\mathcal {L}, I, (G_\zeta )_{\zeta \in \mathcal {L}})$ maps the formal inverse $\overline{a}$ to the inverse of a in base group $G_{{{\,\textrm{alph}\,}}(a)}$. A trace $u \in M(\Gamma \cup \overline{\Gamma },I)$ is reduced with respect to the RAAG $G(\Gamma ,I)$ if it does not contain a factor $a\overline{a}$ or $\overline{a}a$ with $a \in \Gamma$. In particular, every trace from $M(\Gamma ,I)$ is reduced with respect to $G(\Gamma ,I)$, even if it is non-reduced in our sense (i.e., with respect to the graph product ${{\,\textrm{GP}\,}}(\mathcal {L}, I, (G_\zeta )_{\zeta \in \mathcal {L}})$).

An I-clique is a trace $a_1 a_2 \cdots a_k \in M$ such that $a_i \in \Gamma$ and $(a_i,a_j) \in I$ for all $i \ne j$. Note that $|v| \le \sigma$ for every I-clique v. The following lemma is a generalization of a statement from [15] (equation (21) in the proof of Lemma 22), where only the case $q=1$ is considered.

Lemma 14

Let $p,q,r,s \in M$ such that $pq, qr, s \in {{\,\textrm{IRR}\,}}(T)$ and $p\,q\,r \overset{*}{\underset{T}{\Longrightarrow }} s$. Then there exist factorizations

$$ p =_M p' t \, u, \qquad r =_M u^{-1} v\, r', \qquad s =_M p' q\, w\, r' $$

with the following properties:

• t, v, w are I-cliques with $tv \overset{*}{\underset{T}{\Longrightarrow }} w$,

• ${{\,\textrm{alph}\,}}(t) = {{\,\textrm{alph}\,}}(v) = {{\,\textrm{alph}\,}}(w)$, and

• $(q,tu) \in I$ (hence also $(q,v), (q,w) \in I$).

Proof

We prove the lemma by induction over the length of $T$-derivations (recall that T is terminating). The case that $p\,q\,r \in {{\,\textrm{IRR}\,}}(T)$ is clear (take $t = u = v = w = 1$). Now assume that $p\,q\,r$ is not reduced. Since $pq, qr \in {{\,\textrm{IRR}\,}}(T)$, the trace $p\,q\,r$ must contain a factor ab with ${{\,\textrm{alph}\,}}(a) = {{\,\textrm{alph}\,}}(b)$, where a is a maximal letter of p, b is a minimal letter of r and $(a,q), (b,q) \in I$. Let us write $p =_M \tilde{p} a$ and $r =_M b \tilde{r}$.

We distinguish two cases. If $[ab] = 1$, i.e., $b = a^{-1}$, then

$$ p\,q\,r \ =_M\ \tilde{p}\, a\, q\, a^{-1} \tilde{r} \ \underset{T}{\Longrightarrow }\ \ \tilde{p} \,q\, \tilde{r} \ \overset{*}{\underset{T}{\Longrightarrow }}\ s . $$

Since $(a,q)\in I$, we must have $\tilde{p} q, q\tilde{r} \in {{\,\textrm{IRR}\,}}(T)$. Hence, by induction we obtain factorizations

$$ \tilde{p} =_M p' t\, x, \qquad \tilde{r} =_M x^{-1} v\, r', \qquad s =_M p' q\, w\, r' $$

with the following properties:

• t, v, w are I-cliques with $tv \overset{*}{\underset{T}{\Longrightarrow }} w$,

• ${{\,\textrm{alph}\,}}(t) = {{\,\textrm{alph}\,}}(v) = {{\,\textrm{alph}\,}}(w)$, and

• $(q,tx) \in I$.

If we set $u = xa$, we obtain exactly the situation from the lemma.

Now assume that $[ab] = c \ne 1$. We obtain

$$ p\,q\,r \ =_M \ \tilde{p}\, a\, q\, b\, \tilde{r} \ \underset{T}{\Longrightarrow }\ \ \tilde{p}\, c\, q\, \tilde{r}\ \overset{*}{\underset{T}{\Longrightarrow }} \ s . $$

Note that $(c,q) \in I$. Since $\tilde{p}\, a\,q, \, b\,q\,\tilde{r} \in {{\,\textrm{IRR}\,}}(T)$, we also have $\tilde{p}\,c\,q, c\,q\,\tilde{r} \in {{\,\textrm{IRR}\,}}(T)$. Hence, by induction we obtain factorizations

$$ \tilde{p} =_M p' t' u, \qquad \tilde{r} =_M u^{-1} v' r', \qquad s =_M p' c\, q\, w' r' $$

with the following properties:

• $t',v',w'$ are I-cliques with $t'v' \overset{*}{\underset{T}{\Longrightarrow }} w'$,

• ${{\,\textrm{alph}\,}}(t') = {{\,\textrm{alph}\,}}(v') = {{\,\textrm{alph}\,}}(w')$, and

• $(cq,t'u) \in I$.

We define $t = t'a$, $v = v'b$, $w = w'c$. These are I-cliques (since $(c,t') \in I$) that satisfy the conditions from the lemma. Moreover, $(c,u) \in I$ implies $(a,u) \in I$ and hence $p =_M \tilde{p}\,a =_M p' t' u \, a =_M p' t' a \, u =_M p' t \, u$. Similarly, we get $r =_M u^{-1} v\, r'$ and $s =_M p' q\, w\, r'$ (using $(c,q) \in I$). $\square$

Since $\Gamma$ might be an infinite alphabet, for inputs of algorithms, we need to encode elements of $\Gamma$ over a finite alphabet. For $\zeta \in \mathcal {L}$ let $\Sigma _\zeta$ be a finite generating set for $G_\zeta$ such that $\Sigma _\zeta \cap \Sigma _\xi = \emptyset$ for $\zeta \ne \xi$. Then $\Sigma = \bigcup _{\zeta \in \mathcal {L}} \Sigma _\zeta$ is a generating set for G. Every element of $\Gamma _\zeta$ can be represented as a word from $\Sigma _\zeta ^*$. However, in general, representatives are not unique. Deciding whether two words $w,v \in \Sigma _\zeta ^*$ represent the same element of $\Gamma _\zeta$ is the word problem for $G_\zeta$. We give more details how to represent power words in Section 5.1.1.

Let $\mathcal {C}$ be a countable class of finitely generated groups with finite descriptions. One might for instance take a subclass of finitely (or recursively) presented groups. Then a graph product ${{\,\textrm{GP}\,}}(\mathcal {L}, I, (G_\zeta )_{\zeta \in \mathcal {L}})$ with $G_\zeta \in \mathcal {C}$ for all $\zeta$ has a finite description as well: such a group is given by the finite graph $(\mathcal {L}, I)$ and a list of the finite descriptions of the groups $G_\zeta \in \mathcal {C}$ for $\zeta \in \mathcal {L}$. We denote with ${{\,\textrm{GP}\,}}(\mathcal {C})$ the class of all such graph products.

2.7 Complexity

We assume that the reader is familiar with the complexity classes P and $\textsf{NP}$; see e.g. [5] for details. Let $\mathcal {C}$ be any complexity class and $K\subseteq \Delta ^*$, $L \subseteq \Sigma ^*$ languages. Then L is $\mathcal {C}$-many-one reducible to K ($L\le _{\textrm{m}}^{\mathcal {C}} K$) if there exists a $\mathcal {C}$-computable function $f:\Sigma ^* \rightarrow \Delta ^*$ with $x\in L$ if and only if $f(x) \in K$.

2.7.1 Circuit Complexity

We use circuit complexity for classes below deterministic logspace ($\textsf{L}$ for short). Instead of defining these classes directly, we introduce the slightly more general notion of $\textsf{AC}^{0}$-Turing reducibility. A language $L \subseteq \{0,1\}^*$ is $\textsf{AC}^{0}$-Turing-reducible to $K \subseteq \{0,1\}^*$ if there is a family of constant-depth, polynomial-size Boolean circuits with oracle gates for K deciding L. More precisely, we can define the class of language $\textsf{AC}^{0} (K)$ which are $\textsf{AC}^{0}$-Turing-reducible to $K \subseteq \{0,1\}^*$: a language $L \subseteq \{0,1\}^*$ belongs to $\textsf{AC}^{0} (K)$ if there exists a family $(C_n)_{n \ge 0}$ of Boolean circuits with the following properties:

• $C_n$ has n distinguished input gates $x_1, \ldots , x_n$ and a distinguished output gate o.

• $C_n$ accepts exactly the words from $L \cap \{0,1\}^n$, i.e., if the input gate $x_i$ receives the input $a_i \in \{0,1\}$ for all i, then the output gate o evaluates to 1 if and only if $a_1 a_2 \cdots a_n \in L$.

• Every circuit $C_n$ is built up from input gates, not-gates, and-gates, or-gates, and oracle gates for K (which output 1 if and only if their input is in K). The incoming wires for an oracle gate for K have to be ordered since the language K is not necessarily closed under permutations of symbols.

• All gates may have unbounded fan-in, i. e., there is no bound on the number of incoming wires for a gate.

• There is a polynomial p(n) such that $C_n$ has at most p(n) many gates and wires.

• There is a constant d such that every $C_n$ has depth at most d (the depth is the length of a longest path from an input gate $x_i$ to the output gate o).

This is in fact the definition of non-uniform $\textsf{AC}^{0} (K)$. Here “non-uniform” means that the mapping $n \mapsto C_n$ is not restricted in any way. In particular, it can be non-computable. For algorithmic purposes one usually adds some uniformity requirement to the above definition. The most “uniform” version of $\textsf{AC}^{0} (K)$ is $\textsf{DLOGTIME}$-uniform $\textsf{AC}^{0} (K)$. For this, one encodes the gates of each circuit $C_n$ by bit strings of length $\mathcal {O}(\log n)$. Then the circuit family $(C_n)_{n \ge 0}$ is called $\textsf{DLOGTIME}$-uniform if (i) there exists a deterministic Turing machine that computes for a given gate $u \in \{0,1\}^*$ of $C_n$ ($|u| \in \mathcal {O}(\log n)$) in time $\mathcal {O}(\log n)$ the type of gate u, where the types are $x_1, \ldots , x_n$, not, and, or, oracle gate, and (ii) there exists a deterministic Turing machine that decides for two given gates $u,v \in \{0,1\}^*$ of $C_n$ ($|u|, |v| \in \mathcal {O}(\log n)$) and a binary encoded integer i with $\mathcal {O}(\log n)$ many bits in time $\mathcal {O}(\log n)$ whether u is the i-th input gate for v. In the following, we write $\textsf{uAC}^0 (K)$ for $\textsf{DLOGTIME}$-uniform $\textsf{AC}^{0} (K)$. For more details on these definitions we refer to [60]. If the language L (or K) in the above definition of $\textsf{uAC}^0 (K)$ is defined over a non-binary alphabet $\Sigma$, then one first has to fix a binary encoding of $\Sigma$ as words in $\{0,1\}^\ell$ for some large enough $\ell \in \mathbb {N}$.

If $\mathcal {C} = \{K_1, \ldots , K_n\}$ is a finite class of languages, then $\textsf{AC}^{0} (\mathcal {C})$ is the same as $\textsf{AC}^{0} ( \{ (w,i) \mid i \in [1,n], w \in K_i\} )$. If $\mathcal {C}$ is an infinite complexity class, then $\textsf{uAC}^0 [\mathcal {C}]$ is the union of all classes $\textsf{uAC}^0 (K)$ for $K \in \mathcal {C}$. Note that $\textsf{uAC}^0 [\mathcal {C}](K)$ is the same as $\bigcup _{L \in \mathcal {C}} \textsf{uAC}^0 (K,L)$.

The class $\textsf{uNC}^{1}$ is defined as the class of languages accepted by $\textsf{DLOGTIME}$-uniform families of Boolean circuits having bounded fan-in, polynomial size, and logarithmic depth. As a consequence of Barrington’s theorem [6], we have $\textsf{uNC}^{1} = \textsf{uAC}^0 (\text {WP}(A_5))$, where $A_5$ is the alternating group over 5 elements [60, Corollary 4.54]. Moreover, the word problem for any finite group G is in $\textsf{uNC}^{1}$. If G is finite non-solvable, its word problem is $\textsf{uNC}^{1}$-complete – even under $\textsf{uAC}^0$-many-one reductions. Robinson proved that the word problem for the free group $F_2$ is $\textsf{uNC}^{1}$-hard [56], i.e., $\textsf{uNC}^{1} \subseteq \textsf{uAC}^0 (\text {WP}(F_2))$.

The class $\textsf{uTC}^0$ is defined as $\textsf{uAC}^0 ({\textsc {Majority}})$ where Majority is the language of all bit strings containing more 1s than 0s.

Important problems that are complete (under $\textsf{uAC}^0$-Turing reductions) for $\textsf{uTC}^0$ are:

• the languages $\{ w \in \{0,1\}^* \mid |w|_0 \le |w|_1 \}$ and $\{ w \in \{0,1\}^* \mid |w|_0 = |w|_1 \}$, where $|w|_a$ denotes the number of occurrences of a in w, see e.g. [60],

• the computation (of a certain bit) of the binary representation of the product of two or any (unbounded) number of binary encoded integers [29],

• the computation (of a certain bit) of the binary representation of the integer quotient of two binary encoded integers [29],

• the word problem for every infinite finitely generated solvable linear group [35],

• the conjugacy problem for the Baumslag-Solitar group $\textsf{BS}(1,2)$ [16].

2.7.2 Counting Complexity Classes

Counting complexity classes are built on the idea of counting the number of accepting and rejecting computation paths of a Turing machine. For a non-deterministic Turing machine M, let ${\text {accept}}_M$ (resp., ${\text {reject}}_M$) be the function that assigns to an input x for M the number of accepting (resp., rejecting) computation paths on input x. We define the function ${\text {gap}}_M :\Sigma ^* \rightarrow \mathbb {Z}$ by ${\text {gap}}_M(x) = {\text {accept}}_M(x) - {\text {reject}}_M(x)$. The class of functions $\textsf{GapL}$ and the class of languages $\textsf{C}_=\textsf{L}$ are defined as follows:

$$\begin{aligned} \textsf{GapL}&= \left\{ {\text {gap}}_M \;\vert \; \begin{matrix} M \text { is a non-deterministic, logarithmic space-bounded}\\ \text {Turing machine} \end{matrix} \right\} \\ \textsf{C}_=\textsf{L}&= \left\{ L \;\vert \; \text {there is } f \in \textsf{GapL} \text { with } \forall w \in \Sigma ^* : w \in L \Longleftrightarrow f(w) = 0 \right\} \end{aligned}$$

We write $\textsf{GapL} ^K$ and $\textsf{C}_=\textsf{L} ^{K}$ to denote the corresponding classes where the Turing machine M is equipped with an oracle for the language K. We have the following relationships of $\textsf{C}_=\textsf{L}$ with other complexity classes; see e. g.,  [1]:

$$ \textsf{uTC} ^0 = \textsf{uAC} ^0(\text {WP}(\mathbb {Z})) \subseteq \textsf{uAC} ^0(\text {WP}(F_2)) \subseteq \textsf{L} \subseteq \textsf{NL} \subseteq \textsf{C}_=\textsf{L} \subseteq \textsf{uAC} ^0(\textsf{C}_=\textsf{L}) $$

3 Groups with an Easy Power Word Problem

In this section we start with two easy examples of groups where the power word problem can be solved efficiently.

Theorem 15

If G is a finitely generated nilpotent group, then ${{\,\textrm{PowWP}\,}}(G)$ is in $\textsf{uTC}^0$.

Proof

In [52], the so-called word problem with binary exponents was shown to be in $\textsf{uTC}^0$. Here the input is a power word $u_1^{x_1} \cdots u_n^{x_n}$ but all the $u_i$ are required to be one of the standard generators of the group G. For arbitrary power words, we can apply the same techniques as in [52]: we compute Mal’cev normal forms of all $u_i$ using [52, Theorem 5], then we use the power polynomials from [52, Lemma 2] to compute Mal’cev normal forms with binary exponents of all $u_i^{x_i}$. Finally, we compute the Mal’cev normal form of $u_1^{x_1} \cdots u_n^{x_n}$ again using [52, Theorem 5]. $\square$

Theorem 15 has been generalized in [19], where it is shown that the power word problem for a wreath product $G \wr \mathbb {Z}$ with G finitely generated nilpotent belongs to $\textsf{uTC}^0$. Other classes of groups where the power word problem belongs to $\textsf{uTC} ^0$ are iterated wreath products of the form $\mathbb {Z}^r \wr (\mathbb {Z}^r \wr (\mathbb {Z}^r \cdots ))$, free solvable groups [19] and solvable Baumslag-Solitar group $\textsf{BS}(1,q)$ [45].

The Grigorchuk group (defined in [26] and also known as the first Grigorchuk group) is a finitely generated subgroup of the automorphism group of an infinite binary rooted tree. It is a torsion group (every element has order $2^k$ for some k) and it was the first example of a group of intermediate growth.

Theorem 16

The power word problem for the Grigorchuk group is $\textsf{uAC}^0$-many-one-reducible to its word problem (under suitable assumptions on the input encoding). In particular, the power word problem for the Grigorchuk group is in L.

Proof

Let G denote the Grigorchuk group. By [7, Theorem 6.6], every element of G that can be represented by a word of length m over a finite set of generators has order at most $Cm^{3/2}$ for some constant C. W. l. o. g. $C = 2^\ell$ for some $\ell \in \mathbb {N}$. On input of a power word $u_1^{x_1} \cdots u_n^{x_n}$ with all words $u_i$ of length at most m, we can compute the smallest k with $2^k \ge m$ in $\textsf{uAC}^0$. We have $2^k \le 2m$. Now, we know that an element of length m has order bounded by $2^{2k+\ell }$. Since the order of every element of G is a power of two, this means that $g^{2^{2k+\ell }} = 1$ for all $g \in G$ of length at most m. Thus, we can reduce all exponents modulo $2^{2k+\ell }$ (i. e., we drop all but the $2k+\ell$ least significant bits). Now all exponents are at most $2^{2k+\ell } \le 4Cm^2$ and the power word can be written as an ordinary word (to do this in $\textsf{uAC}^0$, we need a neutral letter to pad the output to a fixed word length). Note that this can be done by a uniform circuit family.

The second statement in the theorem follows from the first statement and the fact that the word problem for the Grigorchuk group is in $\textsf {L}$ (see e. g., [49, 54]). $\square$

The first statement of Theorem 16 only holds if the generating set contains a neutral letter. Otherwise, the reduction is in $\textsf{uTC}^0$.

Recall from the introduction that the compressed word problem for the Grigorchuk group is $\textsf{PSPACE}$-complete [8] and hence provably harder than the power word problem (since $\textsf{L}$ is a proper subset of $\textsf{PSPACE}$).

4 Power Word Problems in Finite Extensions

It is easy to see, that the power word problem of a finite group belongs to $\textsf{uNC}^{1}$. Indeed, we can prove the following more general result (choosing H as the trivial group yields the result for finite groups).

Theorem 17

Let G be finitely generated and let $H\le G$ have finite index. Then ${{\,\textrm{PowWP}\,}}(G)$ is $\textsf{uNC}^{1}$-many-one-reducible to ${{\,\textrm{PowWP}\,}}(H)$.

Proof

Since $H \le G$ is of finite index, there is a normal subgroup $N \le G$ of finite index with $N\le H$ (e. g., $N= \bigcap _{g\in G} gHg^{-1}$). As $N \le H$, ${{\,\textrm{PowWP}\,}}(N)$ is reducible via a homomorphism (i. e., in particular in $\textsf{uTC}^0$) to ${{\,\textrm{PowWP}\,}}(H)$. Thus, we can assume that from the beginning H is normal and that $Q=G/H$ is a finite quotient group. Notice that H is finitely generated as G is so; see e.g. [57, 1.6.11]. Let $R\subseteq G$ denote a set of representatives of Q with $1 \in R$. If we choose a finite generating set $\Sigma$ for H, then $\Sigma \cup (R \setminus \{1\})$ is a finite generating set for G.

Let $u = u_1^{x_1} \cdots u_n^{x_n}$ denote the input power word. As a first step, for every exponent $x_i$ we compute numbers $y_i,z_i \in \mathbb {Z}$ with $x_i = y_i\left| Q \right| + z_i$ and $0 \le z_i < \left| Q \right|$ (i. e., we compute the division with remainder by $\left| Q \right|$). This is possible in $\textsf{uNC}^{1}$ [29]. Note that $u_i^{\left| Q \right| }$ is trivial in the quotient $Q = G/H$ and, therefore, represents an element of H. Using the conjugate collection process from [56, Theorem 5.2] we can compute in $\textsf{uNC}^{1}$ a word $h_i \in \Sigma ^*$ such that $u_i^{\left| Q\right| } =_G h_i$.

Let us give some more details on this process: first recall that $\left| Q\right|$ is a constant. Hence, we can write $u_i^{\left| Q\right| }$ as a word $c_1 s_1 \cdots c_ks_k$ with $c_j \in \Sigma \cup \{1\}$ and $s_j \in R$. Now, let $t_j \in R$ denote the representative of $s_1 \cdots s_{j-1}$ in R (meaning that $t_j H = s_1 \cdots s_{j-1}H$ and $t_1 = 1$ and $t_2 = s_1$) and $q_j \in \Sigma ^*$ such that $q_j =_G t_j s_j t_{j+1}^{-1}$ (note that, indeed, $q_j$ is contained in H). Then we have

$$\begin{aligned}s_j =_G t_{j}^{-1}t_{j} \; s_j \; t_{j+1}^{-1}t_{j+1} =_G t_{j}^{-1}q_jt_{j+1} \end{aligned}$$

and it follows that

$$\begin{aligned} c_1 s_1 \cdots c_ks_k&=_G c_1 \; t_2 c_2 t_2^{-1}\; q_2 \; t_3 c_3 t_3^{-1} \; q_3 \;\cdots \; t_k c_k t_k^{-1} \;q_k\; t_{k+1}. \end{aligned}$$

As $u_i^{\left| Q\right| } \in H$, we have $t_{k+1} = 1$. We can compute $t_j$ for all j in $\textsf{uNC}^{1}$ by solving several instances of the word problem for the finite group Q. After that we can compute $q_j$ by a table look-up (there are only $\left| r\right| ^3$ many possibilities for $t_j$, $s_j$, and $t_{j+1}$). Now it remains to replace each $t_j c_j t_j^{-1}$ by a word over $\Sigma ^*$. As there are only finitely many possibilities for $c_j$ and $t_j$, this can be done even in $\textsf{uNC}^{0}$.

Hence, we have obtained a word $h_i \in \Sigma ^*$ such that $u_i^{\left| Q\right| } =_G h_i$.

As a next step, we replace in the input word every $u_i^{x_i}$ by $h_i^{y_i} u_i^{z_i}$ where we write $u_i^{z_i}$ as a word without exponents (recall that $x_i = y_i\left| Q\right| + z_i$ with $0 \le z_i < \left| Q\right|$). We have obtained a word where all factors with exponents represent elements of H. Finally, we again proceed like Robinson [56] for the ordinary word problem treating words with exponents as single letters (this is possible because they are in H).

To give some more details for the last step (which works quite similarly to the conjugate collection process described above), let us denote the result of the previous step as $g_0 h_1^{y_1} g_1 \cdots h_n^{y_n} g_n$ with $g_i \in (\Sigma \cup R \setminus \{1\})^*$ and $h_i \in \Sigma ^*$. By [56, Theorem 5.2] we can rewrite in $\textsf{uNC}^{1}$ $g_i$ as $g_i = \tilde{h}_i r_i$ with $r_i \in R$ and $\tilde{h}_i \in \Sigma ^*$. Once again, we follow [56] and write $\tilde{h}_0 r_0 h_1^{y_1} \tilde{h}_1 r_1 \cdots h_n^{y_n} \tilde{h}_n r_n$ as

$$\begin{aligned} \tilde{h}_0 w_0 (a_1 h_1^{y_1} \tilde{h}_1a_1^{-1}) w_1 (a_2 h_2^{y_2} \tilde{h}_2a_2^{-1})w_2 \cdots (a_n h_n^{y_n} \tilde{h}_na_n^{-1})w_na_{n+1} \end{aligned}$$

(4)

where $a_i$ is the representative of $r_0 \cdots r_{i-1}$ in R ($a_0 = 1$) and $w_i = a_i r_i a_{i+1}^{-1}$. The element $(a_i h_i^{y_i} \tilde{h}_ia_i^{-1})$ belongs to H since H is normal in G. It is obtained from $h_i^{y_i} \tilde{h}_i$ by conjugation with $a_i$, i.e., by a homomorphism from a fixed finite set of homomorphisms. Thus, a power word $P_i$ over the alphabet $\Sigma$ with $P_i =_H (a_i h_i^{y_i} \tilde{h}_ia_i^{-1})$ can be computed in $\textsf{uTC}^0$. Also all $w_i$ belong to H, since $a_i r_i$ and $a_{i+1}$ belong to the same coset of H. Moreover, every $w_i$ comes from a fixed finite set (namely $R \cdot R \cdot R^{-1}$) and, thus, can be rewritten to a word $w_i' \in \Sigma ^*$. Now it remains to verify whether $a_{n+1}= 1$ (solving the word problem for Q, which is in $\textsf{uNC} ^1$). If this is not the case, we output any non-identity word in H, otherwise we output the power word $P = \tilde{h}_0 w_0' P_1 w_1' P_2 w_2' \cdots P_n w_n'$. As $a_{n+1}= 1$, we have $P =_G u$. $\square$

5 Power Word Problems in Graph Products

The main results of this section are transfer theorems for the complexity of the power word problem in graph products. We will prove such a transfer theorem for the non-uniform setting (where the graph product is fixed) as well as the uniform setting (where the graph product is part of the input). Before, we will consider a special case, the so called simple power word problem for graph products, in Section 5.1. In Section 5.2 we have to prove some further combinatorial results on traces. Finally, in Section 5.3 we prove the transfer theorems for graph products.

5.1 The Simple Power Word Problem for Graph Products

In this section we consider a restricted version of the power word problem for graph products. Later, we will use this restricted version in our algorithms for the unrestricted power word problem.

Let $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, (G_\zeta )_{\zeta \in \mathcal {L}})$ be a graph product and define $\Gamma _\zeta , \Sigma _\zeta , \Gamma , \Sigma$ as in Section 2.6.5. A simple power word is a word $w = w_1^{x_1} \cdots w_n^{x_n}$, where $w_1, \dots , w_n \in \Gamma$ and $x_1, \dots , x_n \in \mathbb {Z}$ is a list of binary encoded integers. Each $w_i$ encoded as a word over some finite alphabet $\Sigma _\zeta$. Note that this is more restrictive than a power word: we only allow powers of elements from a single base group. The simple power word problem ${{\,\textrm{SPowWP}\,}}(G)$ is to decide whether $w =_G 1$, where w is a simple power word. We also consider a uniform version of this problem. With ${{\,\textrm{USPowWP}\,}}({{\,\textrm{GP}\,}}(\mathcal {C}))$ we denote the uniform simple power word problem for graph products from the class ${{\,\textrm{GP}\,}}(\mathcal {C})$ (see the last paragraph in Section 2.6.5).

Proposition 18

For the (uniform) simple power word problem the following holds.

• Let $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, (G_\zeta )_{\zeta \in \mathcal {L}})$ be a fixed graph product of f.g. groups. Then ${{\,\textrm{SPowWP}\,}}(G) \in \textsf{uAC} ^0\bigl (\{\text {WP}(F_2)\} \cup \{ {{\,\textrm{PowWP}\,}}(G_\zeta ) \mid \zeta \in \mathcal {L}\}\bigr )$.

• Let $\mathcal {C}$ be a non-trivial class of f.g. groups. Then ${{\,\textrm{USPowWP}\,}}({{\,\textrm{GP}\,}}(\mathcal {C}))$ is in $\textsf{C}_=\textsf{L} ^{{{\,\textrm{UPowWP}\,}}(\mathcal {C})}$.

These results are obtained by using the corresponding algorithm for the (uniform) word problem [33, Theorem 5.6.5, Theorem 5.6.14] and replacing the oracles for the word problems of the base groups with oracles for the power word problems in the base groups. The proofs for the non-uniform and uniform case are quite different. Indeed, in the non-uniform case, we can work by induction over the size of the (in-)dependence graph, while for the uniform case we rely on an embedding into some linear space of infinite dimension. Therefore, we split the proofs into two subsections: in Section 5.1.2 we work on the non-uniform case and later, in Section 5.1.3, we develop an algorithm for the uniform case.

5.1.1 Input Encoding

Let us give some details how to encode the input for the (simple) power word problem in graph products. There are certainly other ways to represent the input for our algorithms without changing the complexity; but whenever the encoding is important, we assume that is done as described in this section. We will use blocks of equal size to encode the different parts of the input. This makes it possible that parts of the computation can be done in $\textsf{uAC} ^0$. We assume that there is a letter for $1 \in \Sigma$ representing the group identity.

The input of the power word problem in a graph product is $p_1^{x_1}\cdots p_n^{x_n}$ where $p_i = a_{i,1}\cdots a_{i,m_i} \in \Sigma ^*$ (note that each letter of $\Gamma$ can be written as a word over $\Sigma$). We ensure $m_i \le n$ for each i, by padding the input word with $1^1$, increasing the length n. Then, to ensure that each $p_i$ has length exactly n, we pad with the identity element. Now we can write $p_i = a_{i,1}\cdots a_{i,n}$ with $a_{i,j}\in \Sigma$.

We encode each letter $a \in \Sigma$ as a tuple $(\zeta , a)$ where $\zeta = {{\,\textrm{alph}\,}}(a)$. In the non-uniform case, there is a constant k, such that k bits are sufficient to encode any element of $\mathcal {L}$ and any letter of any $\Sigma _\zeta$ for any $\zeta \in \mathcal {L}$. In the uniform case we encode the elements of $\mathcal {L}$ as well as the elements of each $\Sigma _\zeta$ using n bits. The encoding of a word $p_i$ is illustrated by the following figure.

Encoding a word $p_i$ requires 2nk bits in the non-uniform case and $2n^2$ bits in the uniform case. For the simple power word problem we impose the restriction ${{\,\textrm{alph}\,}}(a_{i,j}) = {{\,\textrm{alph}\,}}(a_{i,k})$ for all $i,j ,k \in \{1, \dots , n\}$, as mixed powers are not allowed.

We combine the above encoding for the words $p_i$ with a binary encoding for the exponents $x_i$ to obtain the encoding of a power word. Each exponent is encoded using n bits. Note that we can do this because, if an exponent is smaller, we can pad it with zeroes and, if an exponent is larger, we can choose a larger n and pad the input word with the identity element 1. This leads us to the following encoding of a power word, which in the non-uniform case uses $(2k+1)n^2$ bits.

In the uniform case, this encoding requires $(2n+1)n^2$ bits. Furthermore, we also need to encode the descriptions of the base groups and the independence graph. By padding the input appropriately, we may assume that there are n base groups and that each can be encoded using n bits. The independence graph can be given as adjacency matrix, using $n^2$ bits.

5.1.2 The Non-uniform Case

Before solving the simple power word problem in G we prove several lemmata to help us achieve this goal. Lemma 19 below is due to Kausch [33]. For this lemma, we have to introduce first some notation and the notion of a semidirect product: Take two groups H and N with a left action of H on N (a mapping $(h, g) \mapsto h \circ g$ for $h \in H$, $g \in N$ such that $1 \circ g = g$, $(h_1 h_2) \circ g = h_1 \circ (h_2 \circ g)$ and for each $h \in H$ the map $g \mapsto h \circ g$ is an automorphism of G). The corresponding semidirect product $N \rtimes H$ is a group with underlying set $N \times H$ and the multiplication is defined by $(n_1, h_1) (n_2, h_2) = (n_1 (h_1 \circ n_2), h_1 h_2)$.

If B is a group and u an arbitrary object, we write $B_u = \{ (g,u) \mid g \in B \}$ for an isomorphic copy of B with multiplication $(g,u) (g',u) = (gg',u)$. In the following let B be finitely generated. We begin by looking at the free product $G \simeq *_{k \in \mathbb {N}} B_k$ of countable many copies of B. Kausch [33, Lemma 5.4.5] has shown that the word problem for G can be solved in $\textsf{uAC} ^0$ with oracle gates for $\text {WP}(B)$ and $\text {WP}(F_2)$. We show a similar result for the simple power word problem. Our proof is mostly identical to the one presented in [33], with only a few changes to account for the different encoding of the input. We use the following lemma on the algebraic structure of G.

Lemma 19

[33, Lemma 5.4.4] Let B be a f.g. group and $G = *_{k\in \mathbb {N}} B_k$. Then, we have $G \simeq F(X) \rtimes B$, where F(X) is a free group with basis

$$\begin{aligned} X = \big \{ (g,k) (g,0)^{-1}\big \vert g \in B \setminus \{1\}, k \in \mathbb {N} \setminus \{0\} \big \} \end{aligned}$$

and $g \in B$ acts on F(X) by conjugating with (g, 0):

$$\begin{aligned} \left( g\;,\;\; (h,k) (h,0)^{-1}\right) \mapsto (g,0) (h,k) (h,0)^{-1} (g,0)^{-1}. \end{aligned}$$

Note that

$$\begin{aligned} (g,0) (h,k) (h,0)^{-1} (g,0)^{-1} = (g,0) (g,k)^{-1} (gh,k) (gh, 0)^{-1} \in F(X). \end{aligned}$$

The choice of $0 \in \mathbb {N}$ in Lemma 19 as the distinguished element from $\mathbb {N}$ is arbitrary.

With Lemma 19, we can solve the simple power word problem for G.

Lemma 20

Let B and G be as in Lemma 19. Given a power word

$$\begin{aligned} w = (w_1,k_1)^{x_1} \cdots (w_n,k_n)^{x_n}\in (B \times \mathbb {N} \times \mathbb {Z})^*, \end{aligned}$$

where the exponents $x_i \in \mathbb {Z}$ are encoded as binary numbers, one can decide in $\textsf{uAC} ^0(\{{{\,\textrm{PowWP}\,}}(B), \text {WP}(F_2) \})$ whether $w =_G 1$.

Proof

By Lemma 19 we have $G \simeq F(X) \rtimes B$. The set X is given by

$$\begin{aligned} X = \{ (g,k)(g,0)^{-1} \; \mid \; g \in B \setminus \{1\},\, k \in \mathbb {N} \setminus \{0\} \} . \end{aligned}$$

Let $\varphi :G \rightarrow B$ be the homomorphism defined by $\varphi (b,k) = b$. We can assume $\varphi (w) = w_1^{x_1}\cdots w_n^{x_n} =_B 1$ as otherwise $w \ne _G 1$. Now our aim is to write w as a member of the kernel of $\varphi$, which is F(X).

Let $g_i = w_1^{x_1}\cdots w_i^{x_i} \in (B \times \mathbb {Z})^*$. Observe that we can construct the $g_i$ in $\textsf{uAC} ^0$. We have

$$\begin{aligned} w =_G (g_1,k_1) \prod _{i=2}^{n} (g_{i-1}, k_i)^{-1} (g_i,k_i) . \end{aligned}$$

Using the fact that $g_n = \varphi (w) =_B 1$ (and hence $(g_n,k_n) =_G 1$), we can rewrite w as part of the kernel over the basis X:

$$\begin{aligned} w&=_G \prod _{i=1}^{n-1} (g_i,k_i) (g_i,k_{i+1})^{-1}\\&=_G \prod _{i=1}^{n-1} (g_i,k_i) (g_i,0)^{-1} (g_i,0) (g_i,k_{i+1})^{-1}\\&=_G \prod _{i=1}^{n-1} (g_i,k_i) (g_i,0)^{-1} \bigl ((g_i,k_{i+1})(g_i,0)^{-1}\bigr )^{-1} . \end{aligned}$$

Next we define a finite subset $Y \subseteq X$ such that $w \in F(Y) \le F(X)$. To achieve this we set

$$\begin{aligned} Y = \{ (g_i,k_i)(g_i,0)^{-1},\, (g_i,k_{i+1})(g_i,0)^{-1}\; \mid \; i \in [1, n-1] \}. \end{aligned}$$

From this definition it follows that $|Y| \le 2(n-1)$. Two elements $(g_i,k) (g_i,0)^{-1}$ and $(g_j,\ell )(g_j,0)^{-1}$ from Y are equal if and only if $k = \ell$ and $g_i g_j^{-1} =_B 1$. Note that $g_i g_j^{-1} =_B 1$ is an instance of ${{\,\textrm{PowWP}\,}}(B)$. Hence, using an oracle for ${{\,\textrm{PowWP}\,}}(B)$ one can decide whether two elements of Y represent the same generator of F(Y).

As a last step we simplify the basis Y by mapping it to the integer interval $[1, 2(n-1)]$. We use the following map $\psi :Y \rightarrow [1, 2(n-1)]$:

$$\begin{aligned} (g_i,k_i)(g_i,0)^{-1}\mapsto & {} \min \{ j \le i \mid (g_i,k_i) =_G (g_j,k_j) \} \\ (g_i,k_{i+1})(g_i,0)^{-1}\mapsto & {} \!\! \left\{ \begin{array}{lc} \min \{ j \le n\!-\!1 \mid (g_i,k_{i+1}) =_G (g_j,k_j) \}\, \text { if such a } j \text { exists,}\\ \min \{ j \le n\!-\!1 \mid (g_i,k_{i+1}) =_G (g_j,k_{j+1}) \}\!+n\!-\!1\, \text {otherwise.} \end{array} \right. \end{aligned}$$

The map $\psi$ can be computed in $\textsf{uAC} ^0$ with oracle gates for ${{\,\textrm{PowWP}\,}}(B)$ and defines an isomorphism between F(Y) and $F([1, 2(n-1)])$. It is well known that the free group $F(\mathbb {N})$ can be embedded into $F_2$ by the mapping $k \mapsto a^{-k} b a^k$. Since this mapping can be computed in $\textsf{uTC} ^0 \subseteq \textsf{uAC} ^0(\text {WP}(F_2))$, we can finally check $w =_{F(Y)} 1$ in $\textsf{uAC} ^0(\{{{\,\textrm{PowWP}\,}}(B), \text {WP}(F_2) \})$. $\square$

For the following lemma we need the notion of an amalgamated product. For groups A, P and Q and injective homomorphisms $\phi :A \rightarrow P$ and $\psi :A \rightarrow Q$ the amalgamated product $P *_{A} Q$ is the free product $P * Q$ modulo the relations $\{ \phi (a) = \psi (a) \mid a \in A \}$. In the following, A is a subgroup of P and Q and $\phi$ and $\psi$ are the identity. The following lemma is due to Kausch [33].³

Lemma 21

[33, Lemma 5.5.2] Let $G = P *_A (B \times A)$ and consider the surjective homomorphism $\pi :G \rightarrow P$ with $\pi (g) = g$ for $g \in P$ and $\pi (b) = 1$ for all $b \in B$. Then we have $G \simeq (\ker \pi ) \rtimes P$ and

$$\begin{aligned} \ker \pi \ \simeq \ *_{v \in P / A} B_v\text {,} \end{aligned}$$

where the isomorphism $\varphi :*_{v \in P / A} B_v \rightarrow \ker \pi$ maps (b, v) to $v b v^{-1}$.

We want to solve the simple power word problem by induction on the size of $\mathcal {L}$. For the inductive step, we actually will need to solve the following slightly more general problem:

Definition 22

Let G be a graph product and $H \le G$ a fixed subgroup. We denote by ${{\,\textrm{GSPowWP}\,}}(G, H)$ the generalized simple power word problem:

$\textsf {Input}$:

A list of elements $a_1, \dots , a_n \in \Gamma$ and a list of binary encoded integers $x_1, \dots , x_n \in \mathbb {Z}$.

$\textsf {Output}$:

Does $a_1^{x_1} \cdots a_n^{x_n} \in H$ hold?

Lemma 23

Let $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, (G_\zeta )_{\zeta \in \mathcal {L}})$ be a graph product of f.g. groups. For a subset $S \subseteq \mathcal {L}$ we define the induced subgroup $G_S = {{\,\textrm{GP}\,}}(S, I_S, (G_\zeta )_{\zeta \in S})$, where $I_S = I \cap (S \times S)$. We have

$$\begin{aligned} {{\,\textrm{GSPowWP}\,}}(G_S, G) \in \textsf{uAC} ^0({{\,\textrm{SPowWP}\,}}(G)), \end{aligned}$$

that is the generalized simple power word problem ${{\,\textrm{GSPowWP}\,}}(G_S, G)$ can be decided in $\textsf{uAC} ^0$ with an oracle for the simple power word problem in G.

Proof

Consider the projection $\pi :\Gamma ^* \mapsto \Gamma _S^*$ (where $\Gamma _S = \bigcup _{ \zeta \in S} \Gamma _\zeta$), with

$$\begin{aligned} \pi (a) = \left\{ \begin{matrix} a\quad &{}\text {if }{{\,\textrm{alph}\,}}(a) \in S,\\ 1 &{} \text {otherwise.} \end{matrix}\right. \end{aligned}$$

Let $w = a_1^{x_1}\cdots a_n^{x_n}$ be the input to the generalized simple power word problem and let $\pi (w) = \pi (a_1)^{x_1}\cdots \pi (a_n)^{x_n}$ We have $w =_G \pi (w)$ if and only if $w \in G_S$. This is equivalent to $w^{-1}\pi (w) =_G 1$. Moreover, the projection $\pi$ can be computed in $\textsf{uAC} ^0$ when elements of $\Gamma$ are represented by words from $\bigcup _{\zeta \in \mathcal {L}} \Sigma ^*_\zeta$ (since we assume $1 \in \Sigma$). $\square$

In the following Lemma we prove Part 1 of Proposition 18.

Lemma 24

(Proposition 18, Part 1) Let $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, (G_\zeta )_{\zeta \in \mathcal {L}})$ be a graph product of f.g. groups. We have

$$\begin{aligned} {{\,\textrm{SPowWP}\,}}(G) \in \textsf{uAC} ^0(\{\text {WP}(F_2)\} \cup \{ {{\,\textrm{PowWP}\,}}(G_\zeta ) \mid \zeta \in \mathcal {L}\}), \end{aligned}$$

that is the simple power word problem in G can be solved in $\textsf{uAC} ^0$ with oracles for the power word problem in each base group $G_\zeta$ and the word problem for the free group $F_2$.

Proof

We proceed by induction on the cardinality of $\mathcal {L}$. If $|\mathcal {L}| = 1$, we can solve the simple power word problem in G by solving the power word problem in the base group. Otherwise, fix an arbitrary $\xi \in \mathcal {L}$. We define $\mathcal {L}' = \mathcal {L}\setminus \{\xi \}$, $I' = I \cap (\mathcal {L}' \times \mathcal {L}')$, ${{\,\textrm{link}\,}}(\xi ) = \{\zeta \in \mathcal {L}\mid (\xi , \zeta ) \in I\}$ and the three groups

$$\begin{aligned} P= & {} {{\,\textrm{GP}\,}}(\mathcal {L}', I', (G_\zeta )_{\zeta \in \mathcal {L}'}), \\ A= & {} {{\,\textrm{GP}\,}}({{\,\textrm{link}\,}}(\xi ), I \cap ({{\,\textrm{link}\,}}(\xi ) \times {{\,\textrm{link}\,}}(\xi )),(G_\zeta )_{\zeta \in {{\,\textrm{link}\,}}(\xi )}), \\ B= & {} G_\xi . \end{aligned}$$

Now we can write G as an amalgamated product: $G = P *_A (A \times B)$.

By the induction hypothesis we can solve ${{\,\textrm{SPowWP}\,}}(P)$ and ${{\,\textrm{SPowWP}\,}}(A)$ in $\textsf{uAC} ^0$ with oracles for ${{\,\textrm{PowWP}\,}}(G_\zeta )$ (for all $\zeta \in \mathcal {L}$) and $\text {WP}(F_2)$. By Lemma 23 we can solve ${{\,\textrm{GSPowWP}\,}}(A, P)$ in $\textsf{uAC} ^0$ with an oracle for ${{\,\textrm{SPowWP}\,}}(P)$. It remains to show how to solve the simple power word problem in the amalgamated product.

Let the input be $w = a_1^{x_1} \cdots a_n^{x_n} \in (\Gamma \times \mathbb {Z})^*$. Recall that $\Gamma _\zeta = G_\zeta \setminus \{1\}$ and $\Gamma = \bigcup _{ \zeta \in \mathcal {L}} \Gamma _\zeta$, and let $\Gamma _P = \bigcup _{ \zeta \in \mathcal {L}' } \Gamma _\zeta$ and $\Gamma _B = \Gamma _\xi$. We define the projections $\pi _P:\Gamma ^* \rightarrow \Gamma _P^*$ and $\pi _B:\Gamma ^* \rightarrow \Gamma _B^*$ by

$$\begin{aligned} \pi _P(a)&= \left\{ \begin{matrix} a\quad &{} \text {if } a \in \Gamma _P,\\ 1 &{} \text {if } a \in \Gamma _B, \end{matrix} \right.&\pi _B(a)&= \left\{ \begin{matrix} 1\quad &{} \text {if } a \in \Gamma _P,\\ a &{} \text {if } a \in \Gamma _B . \end{matrix} \right. \end{aligned}$$

Let $p_i = \pi _P(a_i)$ and $b_i = \pi _B(a_i)$. Note that $b_i = 1$ or $p_i = 1$ for all i since w is a simple power word. For the following construction we assume that $\pi _P(w) = p_1^{x_1} \cdots p_n^{x_n} =_P 1$, i.e., $w \in \ker \pi _P$, as otherwise $w \ne _G 1$. By Lemma 21 we have

$$\begin{aligned} G \simeq \left( *_{v \in P / A} B_v \right) \rtimes P, \end{aligned}$$

where $\ker \pi _P \simeq *_{v \in P / A} B_v$. We want to write w as part of $\ker \pi _P$. We define $g_i = p_1^{x_1} \cdots p_i^{x_i}$. Note that the $g_i$ can be computed in $\textsf{uAC} ^0$. We have

$$\begin{aligned} w =_G g_1 b_1^{x_1} g_1^{-1} g_2 b_2^{x_2} \cdots g_{n-1}^{-1}g_n b_n^{x_n}. \end{aligned}$$

Observe that $g_n = \pi _P(w) =_P 1$ and thus

$$\begin{aligned} w =_G g_1 b_1^{x_1} g_1^{-1} \cdots g_n b_n^{x_n} g_n^{-1} \in *_{v \in P / A} B_v, \end{aligned}$$

where we identify every $g_i \in P$ with a coset representative of A. We compute

$$ \mu _i = \min \{ j \in [1,n] \mid g_{i}A = g_{j}A \} = \min \{ j \in [1,n] \mid g_{i}g_j^{-1} \in A\}. $$

The computation can be reduced to ${{\,\textrm{SPowWP}\,}}(P)$ in $\textsf{uAC} ^0$ by Lemma 23.

Now we have $w =_G 1$ if and only if $\pi _P(w) =_P 1$ and

$$\begin{aligned} (b_1, g_{\mu _1}A)^{x_1} \cdots (b_n,g_{\mu _n}A)^{x_n} = 1 \end{aligned}$$

in $*_{v \in P / A} B_v$ or, equivalently, $(b_1,\mu _1)^{x_1} \cdots (b_n,\mu _n)^{x_n} = 1$ in $*_{\mu \in \mathbb {N}} B_\mu$. The lemma follows with Lemma 20. $\square$

5.1.3 The Uniform Case

Let $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, (G_\zeta )_{\zeta \in \mathcal {L}})$ be a graph product of f.g. groups. The following embedding of G into a (possibly infinite-dimensional) linear group has been presented in [33]. We write $\mathbb {Z}^{(\Gamma )}$ for the free abelian group with basis $\Gamma$. It consists of all mappings $f :\Gamma \rightarrow \mathbb {Z}$ such that $f(c) \ne 0$ for only finitely many $c \in \Gamma$. We write such a mapping f as a formal sum $S = \sum _{c \in \Gamma } \lambda _c \cdot c$ with $\lambda _c = f(c) \in \mathbb {Z}$ and call $\lambda _c$ the coefficient of c in S. The mapping $\sigma :G \rightarrow {\text {GL}}(\mathbb {Z}^{(\Gamma )})$ is defined by $w \mapsto \sigma _w$, where $\sigma _w = \sigma _{a_1}\cdots \sigma _{a_n}$ for $w = a_1 \cdots a_n$ with $a_i \in \Gamma$. For $a \in \Gamma$ the mapping $\sigma _a :\mathbb {Z}^{(\Gamma )} \rightarrow \mathbb {Z}^{(\Gamma )}$ is defined as the linear extension of

$$\begin{aligned} \sigma _a(b) = \left\{ \begin{matrix} -a &{} \text {if } a, b \in \Gamma _{\zeta } \text { for some } \zeta \text { and } ab =_{G_\zeta } 1,\\ [ab] - a &{} \text {if } a, b \in \Gamma _{\zeta } \text { for some } \zeta \text { and } ab \ne _{G_\zeta } 1,\\ b + 2a &{}\qquad \qquad \quad \text {if } a \in \Gamma _{\zeta }, b \in \Gamma _{\xi } \text { for some } \zeta \ne \xi \text { and } (\zeta , \xi ) \notin I,\\ b &{} \qquad \qquad \quad \text {if } a \in \Gamma _{\zeta }, b \in \Gamma _{\xi } \text { for some } \zeta \ne \xi \text { and } (\zeta , \xi ) \in I. \end{matrix} \right. \end{aligned}$$

Lemma 25

[33, Lemma 3.3.4] Let $w \in \Gamma ^*$ be reduced, $b \in \Gamma _\xi$ for some $\xi \in \mathcal {L}$ such that $wb =_G ubv$ where $u,v \in \Gamma ^*$, $(b,v) \in I$ and b is the unique maximal letter of ub. Moreover, let

$$\begin{aligned} \sigma _w(b) = \sum _{c\in \Gamma } \lambda _c\cdot c. \end{aligned}$$

For $\zeta \in \mathcal {L}$ write $u = u_{0}a_1 u_1 \cdots a_n u_n$ with $a_i \in \Gamma _\zeta$ and $u_i \in (\Gamma \setminus \Gamma _\zeta )^*$. Then for all $c \in \Gamma _\zeta$ we have $\lambda _c \ge 0$ and

$$\begin{aligned} \lambda _c > 0 \ \Longleftrightarrow \ \text {for some } i \in \{1,\dots , n\} : c =_{G_\zeta } \left\{ \begin{matrix} a_i\cdots a_n &{}\text {if }\zeta \ne \xi \text {,}\\ a_i\cdots a_n b \quad &{}\text {if } \zeta = \xi . \end{matrix} \right. \end{aligned}$$

Algorithm 1

Computing the coefficient of $a \in \Gamma _\zeta$ in $\sigma _w(\chi )$.

Our solution to the uniform simple power word problem is based on the solution to the word problem presented in [33]. The underlying idea is to add an additional free group $\langle \chi \rangle$ for a new generator $\chi$ to the graph product, which is dependent on all other groups. Let $\pi _\zeta$ be the projection onto $\Gamma _\zeta$, defined by $\pi _\zeta (a) = a$ for $a \in \Gamma _\zeta$ and $\pi _\zeta (a) = 1$ for $a \notin \Gamma _\zeta$. As a consequence of Lemma 25 we have $\sigma _w(\chi ) = \chi$ if and only if $w =_G 1$. Non-zero coefficients of $\sigma _w(\chi )$ are coefficients of [u] for a factor u of $\pi _\zeta (w)$ for some $\zeta \in \mathcal {L}$.

Lemma 26

(Proposition 18, Part 2) Let $\mathcal {C}$ be a non-trivial class of f.g. groups. Then ${{\,\textrm{USPowWP}\,}}({{\,\textrm{GP}\,}}(\mathcal {C}))$ belongs to $\textsf{C}_=\textsf{L} ^{{{\,\textrm{UPowWP}\,}}(\mathcal {C})}$.

Proof

Let $w = a_1^{x_1}\cdots a_n^{x_n} \in G$, where $a_i \in \Gamma _{\zeta _i}$ and $x_i \in \mathbb {Z}$. If $w \ne _G 1$ then there are $\zeta \in \mathcal {L}$ and $1 \le k \le \ell \le n$ such that the coefficient of $[\pi _\zeta (a_k^{x_k} \cdots a_\ell ^{x_\ell })]$ in $\sigma _w(\chi )$ is not zero.

To compute the coefficients we use Algorithm 1. For simplicity we assume $a_i^{x_i} \ne _{G_{\zeta _i}} 1$ for all $i \in [1, n]$. This can be enforced by a precomputation using ${{\,\textrm{UPowWP}\,}}(\mathcal {C})$ as an oracle. Let $b_i \in \Gamma _{\zeta _i}$ with $b_i =_{G_{\zeta _i}} a_i^{x_i}$.

Our nondeterministic logspace algorithm will produce a computation tree such that the coefficient of $a \in \Gamma$ in $\sigma _w(\chi )$ will be the number of accepting leaves minus the number of rejecting leaves (as required by the definition of $\textsf{GapL}$). The algorithm stores in each configuration an element $[\pi _{\zeta _k}(b_k \cdots b_\ell )] \in \Gamma$ using the two indices k and $\ell$. We use $(k, \ell ) = (n+1, n+1)$ to represent $\chi$. In addition to k and $\ell$ we store a sign s (1 or $-1$), indicating whether the configuration gives a positive or negative contribution to the coefficient of $[\pi _{\zeta _k}(b_k \cdots b_\ell )]$.

The root node of the computation tree corresponds to $\chi$. Let $w = w'a$, with $a \in \Gamma$. Then $\sigma _w(\chi ) = \sigma _{w'}(\sigma _a(\chi ))$. The nodes on the second level, that is the children of the root node, correspond to $\sigma _a(\chi )$. The last level made up of inner nodes corresponds to $\sigma _w(\chi )$. At that point the algorithm checks if the node corresponds to the input element $a \in \Gamma$, i.e., whether $a = [\pi _{\zeta _k}(b_k\cdots b_\ell )]$ holds. This is done using the oracle for the uniform power word problem in $\mathcal {C}$. If it holds, then the computation will accept the input if the stored sign s is 1, and reject if $s=-1$. If $a = [\pi _{\zeta _k}(b_k\cdots b_\ell )]$ does not hold, then the algorithm branches into two leaf nodes, one accepting and one rejecting, which gives a zero contribution to the coefficient of a. In this way, it is ensured that the coefficient of a is the difference of the number of accepting paths and the number of rejecting paths. Therefore, the computation of a coefficient is in $\textsf{GapL} ^{{{\,\textrm{UPowWP}\,}}(\mathcal {C})}$, and we can check in $\textsf{C}_=\textsf{L} ^{{{\,\textrm{UPowWP}\,}}(\mathcal {C})}$ whether a coefficient is zero. An example of a computation tree is presented in Fig. 2.

Finally, we can check in $\textsf{C}_=\textsf{L} ^{{{\,\textrm{UPowWP}\,}}(\mathcal {C})}$ whether all coefficients of elements $[\pi _{\zeta _k}(b_k\cdots b_\ell )]$ are zero, as $\textsf{C}_=\textsf{L}$ is closed under conjunctive truth table reductions [2, Proposition 17] and the proof holds for every relativized version $\textsf{C}_=\textsf{L} ^{A}$. $\square$

Fig. 2

Computation of the coefficient $\lambda _a$ of $\sigma _{ab}(\chi )$ by Algorithm 1. We assume $(a, b) \in I$. Each inner node is labeled with the coefficient it contributes to. The algorithm stores the coefficient using two indices k and $\ell$. The nodes on the second level correspond to $\sigma _b(\chi ) = 2b+\chi$, the nodes on the third level correspond to $\sigma _{ab}(\chi ) = \sigma _a(2b+\chi ) = 2b+2a+\chi$. If they are labeled with a, they have one leaf node as a child which is an accepting path (or a rejecting path if the sign is negative – here all signs are positive). If they are not labeled with a, then there are two leaf node children, one is an accepting path, the other a rejecting path, so they do not affect the difference of accepting and rejecting paths. Here, the difference of accepting and rejecting paths is 2, which is the coefficient $\lambda _a$ of $\sigma _{ab}(\chi )$

5.2 Combinatorics on Traces

In this section we develop various tools concerning combinatorics on traces, which later will be used to solve the power word problem in graph products. As a motivation and an easy example, we start with the analogous construction for free groups we presented in [43], before looking into the more technical case of graph products. The first task for solving the power word problem in a free group is to compute certain unique normal forms for the words $u_i$ of an instance of the power word problem as in (5) below.

We use the notation from Section 2.6.1. In particular, we use the rewriting system $S_{\textrm{free}}= \{a \overline{a} \rightarrow 1 a \in \Sigma \}$. Fix an arbitrary order on the input alphabet $\Sigma$. This gives us a lexicographic order on $\Sigma ^*$, which is denoted by $\preceq$. Let $\Omega \subseteq {{\,\textrm{IRR}\,}}(S_{\textrm{free}}) \subseteq \Sigma ^*$ denote the set of words w such that

• w is non-empty,

• w is cyclically reduced (i.e, w cannot be written as $a u \overline{a}$ for $a \in \Sigma$),

• w is primitive (i.e, w cannot be written as $u^n$ for $n \ge 2$),

• w is lexicographically minimal among all cyclic permutations of w and $\overline{w}$ (i. e., $w \preceq uv$ for all $u,v \in \Sigma ^*$ with $vu =w$ or $vu = \overline{w}$).

Notice that $\Omega$ consists of Lyndon words [46, Chapter 5.1] with the stronger requirement of being freely reduced, cyclically reduced and also minimal among the conjugacy class of the inverse. In [43], the first step is to rewrite the input power word in the form

$$\begin{aligned} \qquad \qquad w&=s_0u_1^{x_1}s_1 \cdots u_n^{x_n}s_n\qquad \text {with } u_i \in \Omega \text { and } s_i \in {{\,\textrm{IRR}\,}}(S_{\textrm{free}}). \end{aligned}$$

(5)

This transformation can be done by a rather easy $\textsf{uAC}^0 (F_2)$ computation. The reason to do this lies in Lemma 27 below. Essentially it says that, if a long factor of $u_i^{x_i}$ cancels with some $u_j^{x_j}$, then already $u_i= u_j$. It is the most crucial lemma for solving the power word problem for free groups in [43]: The idea is that, if a power word of the form (5) represents the group identity, then, every $u_i$ with a large exponent must cancel with other occurrences of the very same word $u_i$. Thus, only the same $u_i$ can cancel implying that we can make the exponents of different $u_i$ independently smaller.

Lemma 27

Let $p,q \in \Omega$, $x,y \in \mathbb {Z}$ and let v be a factor of $p^x$ and w a factor of $q^{y}$. If $vw \overset{*}{\underset{S_{\textrm{free}}}{\Longrightarrow }} 1$ and $\left| v\right| = \left| w\right| \ge \left| p\right| + \left| Q\right| - 1$, then $p=q$.

Proof

Since p and q are cyclically reduced, v and w are freely reduced, i.e., $v=\overline{w}$ as words. Thus, v has two periods $\left| p\right|$ and $\left| Q\right|$. Since v is long enough, by the theorem of Fine and Wilf [20] it also has the period $\gcd (\left| p\right| ,\left| Q\right| )$. This means that also p and q have period $\gcd (\left| p\right| ,\left| Q\right| )$ (since cyclic permutations of p and q are factors of v). Assuming $\gcd (\left| p\right| ,\left| Q\right| ) < \left| p\right|$, would mean that p is a proper power contradicting the fact that p is primitive. Hence, $\left| p\right| =\left| Q\right|$. Since $\left| v\right| \ge \left| p\right| + \left| Q\right| - 1= 2\left| p\right| -1$, p is a factor of v, which itself is a factor of $q^{-y}$. Thus, p is a cyclic permutation of q or of $\overline{q}$. By the last condition on $\Omega$, this implies $p = q$. $\square$

In the remainder of this section, we develop the requirements for a special normal form (like $\Omega$ above) and generalize Lemma 27 to graph products. In particular, we aim for some special kind of cyclic normal forms ensuring uniqueness within a conjugacy class (see Definition 38 below).

Let us fix a graph product $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, (G_\zeta )_{\zeta \in \mathcal {L}})$ with $G_\zeta$ finitely generated by $\Sigma _\zeta$, define the sets $\Gamma _\zeta = G_\zeta \setminus \{ 1 \}$, $\Gamma = \bigcup _{\zeta \in \mathcal {L}} \Gamma _\zeta$ and $\Sigma = \bigcup _{\zeta \in \mathcal {L}} \Sigma _\zeta$ as before and let $M = M(\Gamma ,I)$ be the corresponding trace monoid.

5.2.1 Cyclic Normal Forms and Conjugacy

Recall that by Lemma 4, traces $u,v \in M$ are conjugate if and only if they are related by a sequence of transpositions.

Lemma 28

([33, Lemma 7.3.8]) Let $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}})$ be a graph product and let $u, v \in M$ be cyclically reduced, connected and composite. Then u and v are conjugate in G if and only if u and v are conjugate in M.

Note that [33, Lemma 7.3.8] requires ${{\,\textrm{alph}\,}}(u) = {{\,\textrm{alph}\,}}(v)$. We do not need this requirement as on the one hand u and v being conjugate in M clearly implies ${{\,\textrm{alph}\,}}(u) = {{\,\textrm{alph}\,}}(v)$, and on the other hand by [33, Lemma 7.3.6] u and v being cyclically reduced and conjugate in G implies ${{\,\textrm{alph}\,}}(u) = {{\,\textrm{alph}\,}}(v)$.

By $\le _\mathcal {L}$ we denote a linear order on the set $\mathcal {L}$. For $a,b \in \Gamma$ we write $a <_{\mathcal {L}} b$ if ${{\,\textrm{alph}\,}}(a) <_{\mathcal {L}} {{\,\textrm{alph}\,}}(b)$. The length-lexicographic normal form of $g \in G$ is the reduced representative ${{\,\textrm{nf}\,}}_G(g) = w \in \Gamma ^*$ for g that is lexicographically smallest. Note that this normal form is on the level of $\Gamma$. Each letter of $\Gamma$ still might have different representations over the finite generating set $\Sigma$ as outlined above. If G is clear from the context, we also write ${{\,\textrm{nf}\,}}(g)$. Moreover, for a word $u \in \Gamma ^*$ (or trace $u \in M$) we write ${{\,\textrm{nf}\,}}(u)$ for ${{\,\textrm{nf}\,}}(g)$, where g is the group element represented by u.

Definition 29

Let $w \in \Gamma ^*$. We say w is a cyclic normal form if w and all its cyclic permutations are length-lexicographic normal forms and w is composite.

Remark 30

Observe that if w is a cyclic normal form, then as a trace from M it is cyclically reduced and all cyclic permutations of w are cyclic normal forms themselves.

Cyclic normal forms have been introduced in [12] for RAAGs. Moreover, by [12], given $w \in \Gamma ^*$, which has a cyclic normal form, a cyclic normal form for w can be computed in linear time. In Theorem 36 below, we show that cyclic normal forms also exist for certain elements in the case of graph products and that they also can be computed efficiently.

It is easy to see that every cyclic normal form is connected (see Remarks 31). In particular, not every element has a cyclic normal form. Moreover, there can be more than one cyclic normal form per conjugacy class; however, by Lemma 33 below they are all cyclic permutations of each other.

Remark 31

Notice that, if $w \in \Gamma ^*$ is a cyclic normal form, then it is connected. Indeed, let $d \in \Gamma$ be a $\le _\mathcal {L}$-largest letter occurring in w. After a cyclic permutation we can write $w = dw'$. Now, assume that $w =_{M} uv$ with $(u,v) \in I$. Without loss of generality d belongs to u. Let c denote the first letter of v. Since $(u,v) \in I$, we must have ${{\,\textrm{alph}\,}}(c) \ne {{\,\textrm{alph}\,}}(d)$ and therefore $c <_\mathcal {L}d$. Since $(c,u) \in I$ we obtain $w =_M cw''$ for some $w''$. But then w cannot start with d, which is contradiction.

For the following considerations, it is useful to embed the trace monoid $M = M(\Gamma ,I)$ (and, thus, ${{\,\textrm{IRR}\,}}(T)$) via the trace monoid $M(\Gamma \cup \overline{\Gamma },I)$ into the right-angled Artin group $G(\Gamma , I)$ as in (3) in Section 2.6.5. Note that this means that we add a formal inverse $\overline{a}$ for every $a \in \Gamma$ (which is different from the inverse $a^{-1}$ of a in the group $G_{{{\,\textrm{alph}\,}}(a)}$). Be aware that $\Gamma$ might be infinite and that a trace $u \in M(\Gamma \cup \overline{\Gamma },I)$ is reduced with respect to $G(\Gamma , I)$ if it does not contain a $a\overline{a}$ or $\overline{a}a$ for $a \in \Gamma$ (but it may contain a factor ab with ${{\,\textrm{alph}\,}}(a) = {{\,\textrm{alph}\,}}(b)$ and therefore be non-reduced with respect to the graph product G).

Lemma 32

Two traces $u,v \in M(\Gamma ,I)$ are conjugate in $M(\Gamma ,I)$ if and only if they are conjugate in the RAAG $G(\Gamma , I)$.

Proof

This follows from [12, Lemma 2.9], which states that traces $u,v \in M(\Gamma \cup \overline{\Gamma },I)$ that are cyclically reduced with respect to the RAAG $G(\Gamma ,I)$ (i.e., no transposition of u or v contains a factor $a\overline{a}$ or $\overline{a}a$ for $a \in \Gamma$) are conjugate in the RAAG $G(\Gamma ,I)$ if and only if u and v are related by a sequence of transpositions. Note that traces $u,v \in M(\Gamma ,I)$ are always cyclically reduced in the RAAG-meaning. Hence, $u,v \in M(\Gamma ,I)$ are conjugate in $G(\Gamma ,I)$ if and only if they are related by a sequence of transpositions, i.e., if and only if they are conjugate in $M(\Gamma ,I)$. $\square$

Lemma 33

Let $u, v\in \Gamma ^*$ be cyclic normal forms. Then u and v are conjugate in G (or, equivalently, conjugate in M by Lemma 28 and Remark 31) if and only if the word u is a cyclic permutation of the word v.

Proof

The lemma can be shown by almost a verbatim repetition of the proof of [12, Proposition 2.21]. However, we can also use that result as a black-box: it states that two cyclic normal forms in a RAAG are conjugate if and only if they are cyclic permutations of each other.⁴

We apply this result to the RAAG $G(\Gamma ,I)$. In [12, Proposition 2.21] it is assumed that $\Gamma$ is finite, whereas our $\Gamma$ is infinite. But we can restrict $\Gamma$ to those symbols that appear in u and v.

Moreover, while we are given a linear order on $\mathcal {L}$, we need a linear order on $\Gamma$ to obtain the notion of a cyclic normal form in a RAAG. To resolve this issue we fix on each $\Gamma _\zeta$ for $\zeta \in \mathcal {L}$ an arbitrary linear order (for different $\zeta ,\xi \in \mathcal {L}$ we use our order on $\mathcal {L}$). This gives a linear order on $\Gamma$. As our definition of ${{\,\textrm{IRR}\,}}(T)$ implies that there are never two consecutive letters from $\Gamma _\zeta$ for the same $\zeta \in \mathcal {L}$, the outcome for the cyclic normal form does not depend on the actual orders we chose on each $\Gamma _\zeta .$ Therefore, every cyclic normal form according to Definition 29 is also a cyclic normal form in the RAAG $G(\Gamma , I)$.

Let us now take two cyclic normal forms $u,v \in \Gamma ^*$ according to Definition 29. Then u and v are also cyclic normal forms with respect to the RAAG $G(\Gamma ,I)$. As traces from $M = M(\Gamma ,I)$, u and v are cyclically reduced, connected and composite. Therefore, by Lemma 28, u and v are conjugate in the graph product G if and only if they are conjugate as traces from $M(\Gamma ,I)$. By Lemma 32 the latter holds if and only if u and v are conjugate in the RAAG $G(\Gamma ,I)$. Finally, [12, Proposition 2.21], tells us that the latter is equivalent to v being a cyclic permutation of u. $\square$

Lemma 34

Let $w = dw' \in \Gamma ^*$ (with $d \in \Gamma$) be a cyclically reduced and composite length-lexicographic normal form such that w does not contain any letter c with $d <_{\mathcal {L}} c$. Then for all $k \ge 1$ we have ${{\,\textrm{nf}\,}}(w^k) = w^k$ and w is a cyclic normal form.

Proof

Note that d must be the unique minimal letter in the trace represented by w: if $a \ne d$ would be also minimal, then $(a,d) \in I$ (in particular, a and d do not belong to the same $\Gamma _\zeta$) and $d <_{\mathcal {L}} a$ (since $dw'$ is a length-lexicographic normal form), contradicting the assumption on d. In particular, w must be connected as a trace.

We show that ${{\,\textrm{nf}\,}}(w^k) = w^k$ by showing that $w^k$ is a length-lexicographic normal form. Since w is cyclically reduced (and hence in particular reduced), connected and composite, also $w^k$ is cyclically reduced and composite.

Let us now prove that $w^k$ is a length-lexicographic normal form: Assume the converse. The characterization of lexicographically smallest words of Anisimov and Knuth [4] implies that $w^k$ contains a factor bua where $a <_{\mathcal {L}} b$ and $(a,bu) \in I$. Since w is a length-lexicographic normal form, the factor bua does not belong to some factor w of $w^k$. Therefore, w has a prefix ya, where y is a suffix of u. Since $(a,y) \in I$, a is a minimal letter of w. Since d is the unique minimal letter of w, we have $d = a$, i.e., $d <_{\mathcal {L}} b$, which contradicts the assumptions on d. Hence, w is indeed a length-lexicographic normal form, i.e., ${{\,\textrm{nf}\,}}(w^k) = w^k$.

Finally, we show that w is a cyclic normal form. Every cyclic permutation v of w is a factor of $w^2$. Since every factor of a length-lexicographic normal form is again a length-lexicographic normal form, v is a length-lexicographic normal form. $\square$

Corollary 35

Let $u = du' \in \Gamma ^*$ (with $d \in \Gamma$) be a cyclic normal form such that u does not contain any letter c with $d <_{\mathcal {L}} c$. If $u =_M w^k$ for a trace w, then ${{\,\textrm{nf}\,}}(w)$ is a cyclic normal form and $u = {{\,\textrm{nf}\,}}(w)^k$ (as words).

Proof

The case $k=1$ is trivial, so let us assume that $k \ge 2$. Let $w \in \Gamma ^*$ such that $u =_M w^k$. By the argument from the proof of Lemma 34, d is the unique minimal letter of u. Since u is composite and connected and ${{\,\textrm{alph}\,}}(u) = {{\,\textrm{alph}\,}}(w)$, also w is composite and connected. As ww is a factor of u, ww must be reduced. Hence, w is cyclically reduced. We can also write w as $w =_M dw'$ and d is also the unique minimal letter of w. In particular, ${{\,\textrm{nf}\,}}(w) = d v$ for some word $v \in \Gamma ^*$. Applying Lemma 34 (with w replaced by ${{\,\textrm{nf}\,}}(w)$) we obtain that ${{\,\textrm{nf}\,}}(w^k) = {{\,\textrm{nf}\,}}({{\,\textrm{nf}\,}}(w)^k) = {{\,\textrm{nf}\,}}(w)^k$ and ${{\,\textrm{nf}\,}}(w)$ is a cyclic normal form. $\square$

Theorem 36

The following holds:

• Let $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}})$ be a graph product of f.g. groups. Then the following problem is in $\textsf{uTC} ^0 \subseteq \textsf{uAC} ^0(\text {WP}(F_2))$:

  $\textsf {Input:}$:

  a cyclically reduced, composite and connected $w \in \Gamma ^*$

  $\textsf {Output:}$:

  a cyclic normal form that is conjugate in G to w

• Let $\mathcal {C}$ be any non-trivial class of f.g. groups. Then the following problem is in $\textsf{uAC} ^0[\textsf{NL} ]$:

  $\textsf {Input:}$:

  $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}})$ given by $(\mathcal {L},I)$ and $G_\zeta \in \mathcal {C}$ for $\zeta \in \mathcal {L}$ and a cyclically reduced, composite and connected $w \in \Gamma ^*$

  $\textsf {Output:}$:

  a cyclic normal form that is conjugate in G to w

In both cases the output word starts with a letter that is maximal w. r. t. $\le _\mathcal {L}$.

The restriction to cyclically reduced, composite and connected inputs in the previous theorem is quite natural. It guarantees the existence of a cyclic normal form. We will see in Section 5.3.1, that creating those conditions has similar complexity: Computing a cyclically reduced conjugate additionally requires an oracle for the (uniform) word problem in the graph product. Splitting a trace into connected traces and checking whether they are composite is in $\textsf{uAC} ^0(\text {WP}(F_2))$ (or $\textsf{uAC} ^0[\textsf{NL} ]$ in the uniform case).

Note that due to Lemma 28, in the situation of Theorem 36, being conjugate in G is equivalent to being conjugate in the trace monoid $M = M(\Gamma ,I)$ or being related by a sequence of transpositions.

Proof of Theorem 36 Let $w \in \Gamma ^*$ be the input word. Note that w is already cyclically reduced, composite and connected. The cyclic normal form can be computed with the following algorithm:

• 1. Compute the length-lexicographic normal form $\tilde{w} = {{\,\textrm{nf}\,}}_G(w^\sigma )$ where, as before, $\sigma = \left| \mathcal {L}\right|$.

• 2. Let $\tilde{w} = y d z$, where $d \in \Gamma _\zeta$ is such that $\zeta$ is maximal w. r. t. $\le _\mathcal {L}$, $y \in (\Gamma \setminus \Gamma _\zeta )^*$ and $z \in \Gamma ^*$. Compute the cyclic permutation dzy. That is, we rotate the first occurrence of d to the front.

• 3. Compute the length-lexicographic normal form of dzy. We have ${{\,\textrm{nf}\,}}_G(d z y) = u^\sigma$, where u is a cyclic normal form conjugate to w.

First, we show that our algorithm is correct, i. e., ${{\,\textrm{nf}\,}}_G(d z y)$ has the form $u^\sigma$ and u is a cyclic normal form conjugate to w.

For this we first prove that d is the unique minimal letter of the trace represented by dzy. To get a contradiction, assume that $a \ne d$ is another minimal letter. In particular, $(a,d) \in I$, which implies $a <_{\mathcal {L}} d$. If a belongs to z, then we can write $z = az'$ and get $ydz =_M yadz'$ contradicting the fact that ydz is a length-lexicographic normal form. Now assume that a belongs to y, i.e., $y =_M a y'$ and $(a, dz) \in I$. Hence, in the trace monoid M, ya is a prefix of $w^{2\sigma } =_M (ydz) (ay'dz)$. Levi’s Lemma yields the following diagram (where $yav =_M w^{2\sigma }$):

None of the $v_i$ can be 1, since d belongs to w but not to ya. By Lemma 6 we obtain $y_j = 1$ for all $j \ge \sigma$. In particular, ya is already a prefix of $w^\sigma =_M ydz$. But a does not occur in dz (we have $(a, dz) \in I$). Hence, since ya contains more a’s than y, this is a contradiction.

Next, let us show that y is a prefix of wy in the trace monoid M. To see this, observe that $ydzw =_M w^{\sigma +1} =_M wydz$. Since $\left| y\right| _a \le \left| wy \right| _a$ for all $a \in \Gamma$, Lemma 7 implies that y is a prefix of wy.

Thus, we can find some $\hat{u} \in M$ with $y\hat{u} =_M wy$. Observe that by the very definition $\hat{u}$ is conjugate to w. By Lemma 4, $\hat{u}$ can be obtained from the cyclically reduced w by a sequence of transpositions. Since the property of being cyclically reduced is preserved by transpositions, it follows that also $\hat{u}$ is cyclically reduced.

Since $y \hat{u}^\sigma =_M w^\sigma y =_M y dz y$ and M is cancellative, we get $d z y =_M \hat{u}^\sigma$. In particular, d is the unique minimal letter of $\hat{u}$. Therefore, by Lemma 34, ${{\,\textrm{nf}\,}}_G(d z y) = {{\,\textrm{nf}\,}}_G(\hat{u}^{\sigma }) = {{\,\textrm{nf}\,}}_G(\hat{u})^{\sigma }$ and $u = {{\,\textrm{nf}\,}}_G(\hat{u})$ is a cyclic normal form.

Second, we look at the complexity in the non-uniform case. Our algorithm requires solving the normal form problem twice. Since the input is cyclically reduced, computing the normal form only requires computing a lexicographically smallest ordering, which by [33, Theorem 6.3.7] can be done in $\textsf{uTC} ^0 \subseteq \textsf{uAC} ^0(\text {WP}(F_2))$. In addition, we need to compute a cyclic permutation, which can be done in $\textsf{uAC} ^0$.

Third, we look at the complexity in the uniform case. By [33, Theorem 6.3.13], solving the normal form problem can be done in $\textsf{uTC}^0$ with oracle gates for $\textsf{NL}$ (more precisely, that theorem states that it can be decided in $\textsf{NL}$ which of two letters comes first in the normal form – as sorting is in $\textsf{uTC}^0$, this statement follows). Note that $\textsf{uTC}^0 [\textsf{NL} ] = \textsf{uAC}^0 [\textsf{NL} ]$. Finally, again, the cyclic permutation can be computed in $\textsf{uAC} ^0$. $\square$

Finally, we need the following lemma that requires that none of the base groups $G_\zeta$ contains elements of order two. Hence, $a \ne a^{-1}$ holds for all $a \in \Gamma$.

Lemma 37

Assume that $a \ne a^{-1}$ for all $a \in \Gamma$. If $p \in M \setminus \{1\}$ is reduced, then p and $p^{-1}$ are not conjugate (in M).

Proof

Assume that $p \in M \setminus \{1\}$ is conjugate to $p^{-1}$. We show that p is not reduced. Let us first consider the case that $p =_M p^{-1}$. We show by induction on |p| that p is not reduced. Since $p \ne 1$, we can write $p =_M a s$ for $a \in \Gamma$ and $s \in M$. We obtain $a s =_M p =_M p^{-1} =_M s^{-1} a^{-1}$. Since $a \ne a^{-1}$, we can write s as $s =_M t a^{-1}$ and obtain $a t a^{-1} =_M as =_M s^{-1} a^{-1} =_M a t^{-1} a^{-1}$. Since M is cancellative, we get $t =_M t^{-1}$. If $t=1$, then $p _M= aa^{-1}$ is not reduced and, if $t \ne 1$, then t is not reduced by induction.

Now assume that $p \ne p^{-1}$. Since p and $p^{-1}$ are conjugate, [14, Proposition 4.4.5] yields factorizations $p =_M q_1 q_2 \cdots q_k$ and $p^{-1} =_M q_k q_{k-1} \cdots q_1$ for traces $q_1, \ldots , q_k \in M \setminus \{1\}$. Define $r =_M q_2 \cdots q_k$ and $s =_M q_2^{-1} \cdots q_k^{-1}$. We obtain $q_1 r =_M q_1^{-1} s$. Levi’s Lemma yields factorizations $q_1 =_M t u$ and $q_1^{-1} =_M t v$ with $(u,v) \in I$.

We claim that $u=v=1$: For every $\zeta \in \mathcal {L}$, the number of letters from $\Gamma _\zeta$ in $q_1$ and $q_1^{-1}$ is the same. Hence, also the number of letters from $\Gamma _\zeta$ in u and v is the same. Since $(u,v) \in I$, this is only possible if $u=v=1$.

We now get $q_1 = q_1^{-1}$. By the first paragraph of the proof, this shows that $q_1$ (and hence p) is not reduced.$\square$

5.2.2 A Variant of Lyndon Traces

A Lyndon trace w from a trace monoid $M(\Sigma ,I)$ is a connected primitive trace that is lexicographical minimal in its conjugacy class (where a trace u is smaller than a trace v if the lexicographic normal form of u is length-lexicographically smaller than the lexicographic normal form of v), see e.g. [14, Section 4.4]. We will work with the following variant of Lyndon traces. It is analogue to the definition of $\Omega$ we gave at the beginning of Section 5.2 for free groups. In the rest of the paper $\Omega$ will always refer to the set in Definition 38 below (and no longer to the set $\Omega$ from Section 5.2). As usual let $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}})$ be a graph product and $M = M(\Gamma , I)$ the corresponding trace monoid.

Definition 38

Let $\Omega$ be the set of all $w \in \Gamma ^*$ satisfying the following properties:

• w is a cyclic normal form (in particular, it is composite, cyclically reduced, and connected),

• w represents a primitive element of M,

• w is lexicographically minimal (w. r. t. $\le _\mathcal {L}$) among its cyclic permutations and the cyclic permutations of a cyclic normal form conjugate (in M) to $w^{-1}$.

Note that the last point in Definition 38 makes sense because if w is composite, cyclically reduced, connected and primitive, then $w^{-1}$ as well as every $w'$ conjugate in M to w or $w^{-1}$ have the same properties (it follows from Lemma 5 that a trace conjugate to a primitive trace is also primitive). Moreover, by Theorem 36 there is a cyclic normal form that is conjugate to $w^{-1}$ and by Lemma 33 all cyclic normal forms conjugate to $w^{-1}$ are cyclic permutations of each other.

Remark 39

Note that if $u,v \in \Omega$ and the traces represented by u and v are conjugate in M (or equivalently G), then $u = v$: By Lemma 33, u and v are cyclic permutations of each other, and the last point of Definiton 38 implies that $u=v$. If $u^{-1}$ and $v^{-1}$ are conjugate in M, then also u and v are conjugate in M, and we obtain again $u=v$. Finally, assume that u and $v^{-1}$ are conjugate in M. Fix a cyclic normal form w that is conjugate to $v^{-1}$. Hence, u and w are conjugate in M and by Lemma 33, u is a cyclic permutation of w. So, u is a cyclic permutation of a cyclic normal form conjugate to $v^{-1}$, which implies $v \le _{\mathcal {L}} u$. Since also $u^{-1}$ and v are conjugate in M, we also have $v \le _{\mathcal {L}} u$ and, thus, $u=v$.

Example 40

Notice that the elements of $\Omega$ are not really Lyndon traces. This is because they are only minimal among their cyclic permutations but not minimal in the full conjugacy class. Indeed, consider the trace monoid $M(\Sigma ,I)$ where $\Sigma = \{a,b,c\}$, $I = \{(a,c),(c,a)\}$, and $a< b < c$.⁵ Then the trace abc is lexicographically smallest in its conjugacy class. However, it is not a cyclic normal form, since the cyclic permutation bca is not lexicographically minimal. The corresponding lexicographically smallest conjugate cyclic normal form would be acb.

Remark 41

Notice that, when solving the uniform power word problem for graph products, it is important that in $\Omega$ we require lexicographical minimality only among cyclic normal forms conjugate to $w^{\pm 1}$. A straightforward generalization of the approach for free groups (see beginning of Section 5.2) would search for a lexicographically minimal element in the full conjugacy class of $w^{\pm 1}$. However, this approach does not seem to be feasible because there might be exponentially many conjugate traces for a given trace. Here is an example:

Let $M(\Sigma ,I)$ where $\Sigma = \{a_1, \dots , a_n\}$ and $I = \{(a_i,a_j) \left| j-i\right| \ge 2\}$ and $u=a_1\cdots a_n$. Then every permutation $a_{\pi (1)}\cdots a_{\pi (n)}$ is conjugate to u. In particular, there are n! many conjugate traces to u.

An interesting open question is the complexity of the following problem: given a trace monoid and a trace, find the lexicographically smallest conjugate trace. This problem can easily be seen to be in $\textsf {P}^\textsf{NP}$. However, it is totally unclear to us whether it can be actually solved in polynomial time – or whether its decision variant is $\textsf{NP}$-complete.

The crucial property of $\Omega$ is that each $w \in \Omega$ is a unique representative for its conjugacy class and the conjugacy class of its inverse. Similar to the case of a free group (see Lemma 27) this fact leads us to the following theorem, which is central to solving the power word problem in graph products (see Lemma 51 below). As explained before Lemma 27, the intuition behind that lemma is that, if there are two powers $p^x$ and $q^y$ where $p, q \in \Omega$ and $q \ne p$, then in $p^xq^y$ only a small number of letters can cancel out. Conversely, if a sufficiently large suffix of $p^x$ cancels with a prefix of $q^y$, then $p = q$. The same intuition applies to Theorem 42. In the end this will allow us to decrease all the exponents of p simultaneously as described in Definition 56.

Theorem 42

Let ${p}, {q} \in \Omega$, and ${x}, {y} \in \mathbb {Z}$. Moreover, let $u \in M$ (resp., $v \in M$) be a factor of the trace represented by ${p}^{{x}}$ (resp., ${q}^{{y}}$) such that $uv =_G 1$. If $|u| = |v| > 2\sigma (|{p}| + |{q}|)$, then ${p} = {q}$ (recall that $\sigma = |\mathcal {L}|$).

Note that in the above theorem u and v are reduced as they are factors of $p^x$ (resp. $q^y$). For the proof of Theorem 42 we apply the Lemmata 2 and 3 from Section 2.4.2 to the trace monoid $M(\Gamma , I)$ that corresponds to the graph product $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}})$. To do so, we use the cliques and projections as defined in (1) in Section 2.5, which we recall for convenience:

$$\begin{aligned} \{A_1, \ldots , A_k\} = \left\{ \Gamma _\zeta \cup \Gamma _\xi \mid (\zeta , \xi ) \in D, \zeta \ne \xi \right\} \cup \{ \Gamma _\zeta \mid \zeta \text { is isolated} \}, \end{aligned}$$

where $\zeta$ is isolated if there is no $\xi \ne \zeta$ with $(\zeta , \xi ) \in D$. Now, $\pi _i:M(\Gamma , I) \rightarrow A_i^*$ denotes the canonical projection and $\Pi :M(\Gamma , I) \rightarrow A_1^*\times \cdots \times A_k^*$ with $\Pi (w) = (\pi _1(w), \dots , \pi _k(w))$ is an injective monoid morphism by Lemma 2. We derive Theorem 42 from the following lemma.

Lemma 43

Let $p, q, v \in M(\Gamma , I)$, $x, y \in \mathbb {N}\setminus \{0\}$ such that p and q are primitive and connected, and $p^x$ and $q^y$ have the common factor v. If $p^2$ and $q^2$ are factors of v, then for all i the projections $\pi _i(p)$ and $\pi _i(q)$ are conjugate as words.

Proof

Note that ${{\,\textrm{alph}\,}}(p) = {{\,\textrm{alph}\,}}(v) = {{\,\textrm{alph}\,}}(q)$. We define the set

$$\begin{aligned} J_v = \{ i \mid {{\,\textrm{alph}\,}}(A_i) \cap {{\,\textrm{alph}\,}}(v) \ne \emptyset \} . \end{aligned}$$

Note that $\pi _i(p) = \pi _i(q) = 1$ for all $i \in [1,k] \setminus J_v$. It therefore suffices to show that $\pi _i(p)$ and $\pi _i(q)$ are conjugate for all $i \in J_v$.

For each $i \in J_v$ we write $\pi _i(p) = \tilde{p}_i^{s_i}$ and $\pi _i(q) = \tilde{q}_i^{r_i}$ where $\tilde{p}_i$ and $\tilde{q}_i \in A_i^*$ are primitive. As v is a common factor of $p^x$ and $q^y$, its projection $\pi _i(v)$ is a common factor of $\pi _i(p^x) = \tilde{p}_i^{{}s_i x}$ and $\pi _i(q^y) = \tilde{q}_i^{{}r_i y}$. Thus, $\pi _i(v)$ has periods $|\tilde{p}_i|$ and $|\tilde{q}_i|$. Since $p^{2}$ is a factor of v, $\pi _i(p)^{2}$ is a factor of $\pi _i(v)$. This yields the lower bound $2|\tilde{p}_i|$, and by symmetry $2|\tilde{q}_i|$, on the length of $\pi _i(v)$. Combining those, we obtain

$$\begin{aligned} |\pi _i(v)| \ge \max \{2|\tilde{p}_i|, 2|\tilde{q}_i|\} \ge |\tilde{p}_i| + |\tilde{q}_i| \ge |\tilde{p}_i| + |\tilde{q}_i| - 1. \end{aligned}$$

By the theorem of Fine and Wilf [20], $\gcd (|\tilde{p}_i|,|\tilde{q}_i|)$ is a period of $\pi _i(v)$. As $\tilde{p}_i$ and $\tilde{q}_i$ are primitive, it follows that $|\tilde{p}_i| = |\tilde{q}_i|$. As p is a factor of v, in particular, $\tilde{p}_i$ is a factor of $\pi _i(v)$ and, thus, also of $\pi _i(q^y) = \tilde{q}_i^{r_i \cdot y}$. Hence, $\tilde{p}_i$ and $\tilde{q}_i$ are conjugate words for all $i \in J_v$.

In order to show that $\pi _i(p)$ and $\pi _i(q)$ are conjugate for all $i \in J_v$, it suffices to show that $s_i = r_i$ for all $i \in J_v$. Assume for a contradiction that for some $i \in J_v$ we have $s_i \ne r_i$. Then, there are $\lambda , \mu \in \mathbb {N}\setminus \{0\}$ such that $\lambda s_i = \mu r_i$. W. l. o. g. let $\mu > 1$ and $\gcd \{\lambda , \mu \} = 1$. Now $\mu$ divides $s_i$. Let

$$\begin{aligned} J = \{ j \in J_v \mid \lambda s_j = \mu r_j \}. \end{aligned}$$

Claim: $J = J_v$.

Proof of the Claim

Clearly $i \in J$. We want to show that $J = J_v$. This is the case if ${{\,\textrm{alph}\,}}(v) = \{\zeta \}$ for some isolated $\zeta$ (then, also $J_v$ is a singleton). Otherwise, for all $i \in J_v$ the set $A_i$ is of the form $A_i = \Gamma _\zeta \cup \Gamma _\xi$ with $(\zeta ,\xi ) \in D$ and $\zeta \ne \xi$.

Assume now that $J \subsetneq J_v$ and let $j \in J_v \setminus J$. Let $\zeta \in {{\,\textrm{alph}\,}}(v) \cap {{\,\textrm{alph}\,}}(A_i)$ and $\xi \in {{\,\textrm{alph}\,}}(v) \cap {{\,\textrm{alph}\,}}(A_j)$ ($\zeta = \xi$ is possible). Since p (and hence v) is connected, there must exist a (possibly empty) simple path $\zeta = \zeta _0, \zeta _1, \ldots , \zeta _{n-1}, \zeta _n = \xi$ in $({{\,\textrm{alph}\,}}(v), D)$. Each edge $(\nu ,\kappa ) \in D$ along this path corresponds to an element $\Gamma _{\nu } \cup \Gamma _{\kappa } = A_\ell$ with $\ell \in J_v$ and $\nu , \kappa \in {{\,\textrm{alph}\,}}(v)$. Therefore, there are $i' \in J$ and $j' \in J_v \setminus J$ with ${{\,\textrm{alph}\,}}(A_{i'} \cap A_{j'}) = \{\zeta \}$ for some $\zeta \in {{\,\textrm{alph}\,}}(v) = {{\,\textrm{alph}\,}}(p) = {{\,\textrm{alph}\,}}(q)$.

For the further consideration, let us rename $i'$ (resp., $j'$) into i (resp., j). We have $s_j |\tilde{p}_j|_\zeta = |p|_\zeta = s_i |\tilde{p}_i|_\zeta$ (recall that $|p|_\zeta = |p|_{\Gamma _\zeta }$). Similarly, we have $r_j |\tilde{q}_j|_\zeta = |q|_\zeta = r_i|\tilde{q}_i|_\zeta$, which is equivalent to $r_j |\tilde{p}_j|_\zeta = r_i |\tilde{p}_i|_\zeta$ (as $\tilde{p}_\ell$ and $\tilde{q}_\ell$ are conjugate for all $\ell \in J_v$). Since $i \in J$, we obtain

$$\begin{aligned} \lambda s_j |\tilde{p}_j|_\zeta = \lambda s_i |\tilde{p}_i|_\zeta = \mu r_i|\tilde{p}_i|_\zeta = \mu r_j |\tilde{p}_j|_\zeta . \end{aligned}$$

Since $|\tilde{p}_j|_\zeta \ne 0$, we conclude $\lambda s_j = \mu r_j$, i.e., $j \in J$, which is a contradiction. Therefore, we get $J = J_v$, which concludes the proof of the claim.

Thus, every $s_i$ (for $i \in J_v$) is divisible by $\mu > 1$. By Lemma 3 we can write $p =_M u^{\mu }$ for some trace u, contradicting p being primitive. This concludes the proof of the lemma.$\square$

The proof idea for Theorem 42 is as follows: We use the length bound from Lemma 6 in order to show that the requirements of Lemma 43 are satisfied. After applying that lemma, we show that p and q are conjugate using Lemma 2. Then we conclude from the definition of $\Omega$ that $p=q$.

Proof of Theorem 42 We have $u =_G v^{-1}$ and hence $u =_M v^{-1}$ (since, u and $v^{-1}$ are reduced). Thus, $v^{-1}$ is a factor of ${p}^x$ and therefore, v is a factor of ${p}^{-x}$. Let $\Omega ^\pm = \Omega \cup \Omega ^{-1}$ be the extension of $\Omega$ that includes the inverse of each element. Let $\hat{x} = |{x}|$ and $\hat{y} = |{y}|$. Then there are $\hat{p}, \hat{q} \in \Omega ^\pm$ such that $\hat{p} \in \{{p}, {p}^{-1}\}$, $\hat{q} \in \{{q}, {q}^{-1}\}$ and v is a common factor of $\hat{p}^{\hat{x}}$ and $\hat{q}^{\hat{y}}$. As $|v| > 2\sigma (|p| + |q|) \ge 2\sigma |p|$, by Lemma 6, v can be written as $v = u_1\cdots u_t \hat{p}^z v_s \cdots v_1$, where $z \ge 2$. Hence, $\hat{p}^2$ is a factor of v. By symmetry $\hat{q}^2$ is a factor of v.

By Lemma 43, for all i the projections $\pi _i(\hat{p})$ and $\pi _i(\hat{q})$ are conjugate words. In particular, for each $\zeta \in \mathcal {L}$ we have $\left| \hat{p}\right| _\zeta = \left| \hat{q}\right| _\zeta$. Thus, as $\hat{q}$ is a factor of $\hat{p}^{\hat{x}}$, it follows from Lemma 9 that $\hat{p}$ is conjugate in M to $\hat{q}$. Since $p,q \in \Omega$, this finally implies $p=q$; see Remark 39. $\square$

5.3 Main Proofs for the Power Word Problem in Graph Products

In this section we show our main results for graph products as presented in the conference version [58]: In order to solve the power word problem, we follow the outline of [43] (which is for free groups). In particular, our proof also consists of three major steps:

• In a preprocessing step we replace all powers with powers of elements of $\Omega$ (Section 5.3.1).

• We define a symbolic rewriting system which we use to prove correctness (Section 5.3.2).

• We define the shortened word, replacing each exponent with a smaller one, bounded by a polynomial in the input (Section 5.3.3).

Finally, in Section 5.3.4, we combine these steps for the solution of the power word problem.

The main difference to [43] is that here we rely on Theorem 42 instead of [43, Lemma 11] (see Lemma 27), an easy fact about words. This is because the combinatorics of traces/graph products is much more involved than of words/free groups. Furthermore, for free groups we did not have to bother with elements of order two, which led to the mistake in [58, 59] (see Remark 52). Another major difference to the case of free groups is that we need the results for the simple power word problem considered in Section 5.1. Apart from that, all steps are the same (with some minor technical differences).

5.3.1 Preprocessing

Let $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}})$ be a graph product of f.g. groups. As usual, $\sigma = |\mathcal {L}|$. We define the alphabet $\tilde{\Gamma } = \Gamma \times \mathbb {Z}$, where (v, z) represents the power $v^z$. Note that $\tilde{\Gamma }$ is the alphabet of the simple power word problem in G. During preprocessing, the input power word is transformed into the form

$$\begin{aligned} w = u_0 p_1^{x_1} u_1 \cdots p_n^{x_n} u_n, \qquad \text { where } p_i \in \Omega \text { and } u_i \in \tilde{\Gamma }^* \text { for all } i. \end{aligned}$$

(6)

We denote the uniform word problem for graph products with base groups in $\mathcal {C}$ by ${{\,\textrm{UWP}\,}}({{\,\textrm{GP}\,}}(\mathcal {C}))$. For some further thoughts on how to encode the input, see Section 5.1.1. The preprocessing consists of five steps:

Step 1: Cyclically reducing powers. Cyclically reducing every $p_i$ can be done using the procedure from [33, Lemma 7.3.4]. We also need to compute a trace $y_i$ such that $y_i^{-1} p_i y_i$ is cyclically reduced. It follows from the proof of [33, Lemmata 7.3.2 and 7.3.3] that such $y_i$ can be obtained as a prefix of $p_i$. Let us quickly repeat the argument: assume that $p_i$ is already reduced. First one computes the longest prefix $t_i$ of $p_i$ such that $t_i^{-1}$ is also a suffix of $p_i$. Thus we can write $p_i =_M t_i p'_i t_i^{-1}$. The trace $p'_i$ is not necessarily cyclically reduced. But there are elements $a_1, \ldots , a_k, b_1, \ldots , b_k \in \Gamma$ such that ${{\,\textrm{alph}\,}}(a_i) = {{\,\textrm{alph}\,}}(b_i)$ for all i and $(a_i,a_j) \in I$ for $i \ne j$ (in particular, $k \le \sigma$) such that $p'_i = a_1 \cdots a_n \tilde{p}_i b_1 \cdots b_n$ and $\tilde{p}_i [a_1 b_1] \cdots [a_k b_k]$ is cyclically reduced. Let us define the prefix $y_i = t_i a_1 \cdots a_k$ of $p_i$. Then we have $\tilde{p}_i =_G y_i^{-1} p_i y_i$ and $|y_i| \le |p_i|$. We then replace the power $p_i^{x_i}$ with $y_i^{-1} \tilde{p}_i^{x_i} y_i$; moreover, $y_i^{-1}$ and $y_i$ can be merged with $u_{i-1}$ and $u_i$, respectively. Thus we can assume that for the next step the input again has the form $w = u_0 p_1^{x_1} u_1 \cdots p_n^{x_n} u_n$, but now all $p_i$ are cyclically reduced.

Step 2: Replacing powers with powers of connected elements. We compute the connected components of $p_i$. More precisely, we compute $p_{i,1}$, ..., $p_{i,k_i}$ such that each $p_{i, j}$ is connected, $p_i =_G p_{i,1}\cdots p_{i,k_i}$, and $(p_{i,j}, p_{i,\ell }) \in I$ for $j \ne \ell$. Observe that $k_i \le |\mathcal {L}|$. We replace the power $p_i^{x_i}$ with $p_{i,1}^{x_i}\cdots p_{i,k_i}^{x_i}$.

Step 3: Removing powers of a single letter. We use the alphabet $\tilde{\Gamma } = \Gamma \times \mathbb {Z}$, where (v, z) represents the power $v^z$. We replace each power $p_i^{x_i}$ where $p_i \in \Gamma _\zeta$ for some $\zeta \in \mathcal {L}$ with the corresponding letter $p_i^{x_i} \in \tilde{\Gamma }$. Note that there is no real work to do in this step. What happens is that powers of a single letter will be ignored (i. e., treated as if they were part of the $u_i$ from (6)) in the remaining preprocessing steps and when computing the shortened word. As a consequence, in the remaining preprocessing steps and during the computation of the shortened word we may assume that we only have powers of composite words. At the end, powers of a single letter will be the only powers remaining in the shortened word, and therefore they are the reason for reducing to the simple power word problem. For the next step we still assume that the input has the shape $w = u_0 p_1^{x_1} u_1 \cdots p_n^{x_n} u_n$, however, from here on $u_i \in \tilde{\Gamma }^*$.

Step 4: Replace each letter with a normal form specific to the input. Whereas the previous steps work on the level of the trace monoid, this step computes a normal form for the elements of $\Gamma$ itself. For each i we write $p_i = a_{i, 1}\cdots a_{i, k_i}$, where $a_{i, j} \in {\Gamma }$. Recall that elements of $\Gamma$ are given as words over $\Sigma$ i. e., the generators of the respective base groups. Let

$$N = [a_{1, 1},a_{1,1}^{-1}, \ldots , a_{1, k_1},a_{1,k_1}^{-1}, \ldots , a_{n,1},a_{n,1}^{-1}, \ldots , a_{n, k_n},a_{n,k_n}^{-1}]$$

be the list of letters of $\Gamma$ (and their inverses) occurring in some power. For convenience, we write $N = [b_1, \dots , b_{m}]$, where $m = |N|$. We replace each $p_i$ with $\tilde{p}_i = \tilde{a}_{i, 1}\cdots \tilde{a}_{i, k_i}$, where $\tilde{a}_{i, j}$ is the first element in N equivalent to $a_{i, j}$. Note that we need to solve the word problem in the base groups $G_\zeta$ to compute this. After that transformation, any two $\tilde{a}_{i, j}$ and $\tilde{a}_{\ell , m}$ representing the same element of $\Gamma$ are equal as words over $\Sigma$ (and so bit-wise equal). Thus, the letters are in a normal form. Be aware that this normal form is dependent on the input of the power word problem in G, but that is not an issue for our application. Again, we assume the input for the next step to be $w = u_0 p_1^{x_1} u_1 \cdots p_n^{x_n} u_n$.

Step 5: Making each $p_i$ a primitive cyclic normal form. The following is done for each $i \in [1, n]$. Let us write $p^x$ for $p_i^{x_i}$. We apply the algorithm presented in the proof of Theorem 36 and compute a cyclic normal form q that is conjugate to p in M. We have $y p =_M q y$ for some y with $|y| < \sigma \cdot |p|$. We replace $p^{x}$ with $y^{-1} q^{x} y$ and merge $y^{-1}$ with $u_{i-1}$ and y with $u_i$. Note that also q must be connected, composite and cyclically reduced as a trace.

Observe that any cyclic normal form u computed by the algorithm from the proof of Theorem 36 starts with a letter d such that u does not contain any letter c with $d <_{\mathcal {L}} c$. If such a cyclic normal form is not primitive in the trace monoid M, i.e., $u =_M w^k$ with $k > 1$, then, by Corollary 35, $u = {{\,\textrm{nf}\,}}(w)^k$ (as words) and ${{\,\textrm{nf}\,}}(w)$ is a cyclic normal form. Therefore, we compute a primitive word $r\in \Gamma ^*$ such that $q = r^k$ for some $k \ge 1$ and replace $q^x$ by $r^{kx}$ (clearly, $q=r$ if q is already primitive). Also r must be connected, composite and cyclically reduced as a trace. Moreover, r is a cyclic normal form as well, since each cyclic permutation of r is a factor of $q = r^k$ if $k \ge 2$ and hence must be a length-lexicographic normal form. Again, we write the resulting power word as $u_0 p_1^{x_1} u_1 \cdots p_n^{x_n} u_n$ for the next step.

Step 6: Replace each power with a power of an element in $\Omega$. Let $\Omega$ be as in Definition 38. The previous steps have already taken care of most properties of $\Omega$. In addition, Step 4 ensured that individual letters are in a normal form. The only requirement not yet fulfilled is that every $p_i$ must be minimal w. r. t. $\le _\mathcal {L}$ among its cyclic permutations and the cyclic permutations of a cyclic normal form conjugate (in M) to $p_i^{-1}$.

Using Theorem 36, we compute a cyclic normal form $p'_i$ that is conjugate (in M) to $p_i^{-1}$. It must be primitive too: if $p'_i =_M s^\ell$ for some $\ell \ge 1$ and $s \in M$, then $(s^{-1})^\ell$ is conjugate in M to $p_i$, which implies by Lemma 5 that $p_i =_M r^\ell$ for some $r\in M$. As p is primitive, we have $\ell = 1$. Hence, $p'_i$ is primitive.

Finally, we consider all cyclic permutations of $p_i$ and $p'_i$ and take the lexicographically smallest one; call it $\hat{p}_i$. Moreover, let $\iota \in \{-1,1\}$ be such that $\iota = 1$ if $\tilde{p}_i$ is conjugate to $p_i$ and $\iota = -1$ if $\tilde{p}_i$ is conjugate to $p_i^{-1}$. Then we can replace the power $p_i^{x_i}$ by $t_i^{-1} \hat{p}_i^{\iota x_i} t_i$ for an appropriate conjugator $t_i$ of length at most $|p_i|$ (we can choose $t_i$ as a prefix of $\hat{p_i}^{\iota {{\,\textrm{sgn}\,}}(x_i)}$). Finally, $t_i^{-1}$ and $t_i$ can be merged with $u_{i-1}$ and $u_i$, respectively.

Remark 44

Notice that it might happen that $p_i$ is conjugate to $p_i^{-1}$. In this case the outcome of Step 6 is not uniquely defined: $p_i^{x_i}$ could be either replaced by $\tilde{p}_i^{x_i}$ or $\tilde{p}_i^{-x_i}$ (plus some appropriate conjugators). For the preprocessing itself this ambiguity is not a problem; however, it prevents Lemma 51 below from being true. Therefore, in the later steps of our proof, we will require that $a\ne a^{-1}$ for all $a \in \Gamma$, which, by Lemma 37, implies that $p_i$ cannot be conjugate to $p_i^{-1}$.

Lemma 45

The preprocessing can be reduced to the word problem; more precisely:

• Let $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}})$ be a fixed graph product of f.g. groups. Then computing the preprocessing is in $\textsf{uAC} ^0(\text {WP}(G), \text {WP}(F_2))$.

• Let $\mathcal {C}$ be a non-trivial class of f.g. groups. Given $(\mathcal {L},I)$, $G_\zeta \in \mathcal {C}$ for $\zeta \in \mathcal {L}$ and an element w of the graph product $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}})$, the preprocessing can be done in $\textsf{uAC} ^0[\textsf{NL} ]({{\,\textrm{UWP}\,}}({{\,\textrm{GP}\,}}(\mathcal {C}))$.

Proof

We look at the complexity of the individual steps of the preprocessing. For this proof we split step 5 into two parts: a) computing a cyclic normal form and b) making it primitive.

Step	non-uniform	uniform
1. making $p_i$ cyclically reduced	$\textsf{uAC}^0 (\text {WP}(G))$	$\textsf{uAC}^0 ({{\,\textrm{UWP}\,}}({{\,\textrm{GP}\,}}(\mathcal {C})))$
2. making $p_i$ connected	$\textsf{uAC}^0$	$\textsf{uAC}^0 [\textsf{NL} ]$
3. powers of single letters	$\textsf{uAC}^0$	$\textsf{uAC}^0$
4. normal form of letters	$\textsf{uAC}^0 (\{\text {WP}(G_{\zeta }) \mid \zeta \in \mathcal {L}\})$	$\textsf{uAC}^0 ({{\,\textrm{UWP}\,}}(\mathcal {C}))$
5a. making $p_i$ cyclic normal forms	$\textsf{uAC}^0 (\text {WP}(F_2))$	$\textsf{uAC}^0 [\textsf{NL} ]$
5b. making $p_i$ primitive	$\textsf{uAC}^0$	$\textsf{uAC}^0$
6. bringing $p_i$ to $\Omega$	$\textsf{uAC}^0 (\text {WP}(F_2))$	$\textsf{uAC}^0 [\textsf{NL} ]$

Step 1.:

By [33, Lemma 7.3.4], the cyclically reduced conjugate trace for a $p_i$ can be computed in $\textsf{uAC} ^0$ with oracle gates for the word problem in G in the non-uniform case and in $\textsf{uAC} ^0$ with oracle gates for ${{\,\textrm{UWP}\,}}({{\,\textrm{GP}\,}}(\mathcal {C}))$ (the uniform word problem for graph products with base groups in $\mathcal {C}$) in the uniform case. Also the conjugating element (called $y_i$ in Step 1 above) can be computed within the same bound.

Step 2.:

To compute the connected components of a power $p_i^{x_i}$ ($i \in [1,n]$), let us define $\mathcal {L}_i = {{\,\textrm{alph}\,}}(p_i)$ and the symmetric predicate ${\text {con}}_i(\zeta , \xi )$ for $\zeta , \xi \in \mathcal {L}$, which is true if and only if there is a path from $\zeta$ to $\xi$ in the dependence graph $(\mathcal {L}_i, (\mathcal {L}_i \times \mathcal {L}_i) \setminus I)$. If $\zeta$ or $\xi$ does not belong to $\mathcal {L}_i$, then ${\text {con}}_{i}(\zeta , \xi )$ is false. Note that if there is a path from $\zeta$ to $\xi$, then there is a path of length at most $\sigma - 1$. Moreover, there is a path of length exactly $\sigma - 1$, because the complement of I is reflexive. Therefore, in the non-uniform case the following formula is equivalent to ${\text {con}}_{i}(\zeta , \xi )$:

$$\begin{aligned} \exists \nu _1, \dots , \nu _{\sigma } \in \mathcal {L}_i : \nu _1 = \zeta \wedge \nu _{\sigma } = \xi \wedge \bigwedge _{j= 1}^{\sigma - 1} (\nu _j, \nu _{j+1}) \notin I . \end{aligned}$$

In the uniform case computing the predicate ${\text {con}}_{i}$ requires solving the undirected path connectivity problem, which is in $\textsf{NL}$. Furthermore, we define the predicate ${\text {smallest}}_{i}(\zeta )$, which for $\zeta \in \mathcal {L}$ is true if and only if $\zeta \in \mathcal {L}_i$ is the smallest member of $\mathcal {L}$ in the connected component of $(\mathcal {L}_i, (\mathcal {L}_i \times \mathcal {L}_i) \setminus I)$. The following formula is equivalent to ${\text {smallest}}_{i}(\zeta )$:

$$\begin{aligned} \zeta \in \mathcal {L}_i \wedge \forall \xi \in \mathcal {L}: {\text {con}}_{i}(\zeta , \xi ) \rightarrow \zeta \le _{\mathcal {L}} \xi . \end{aligned}$$

We define the projection $\pi _{i, \zeta } :\Gamma ^* \rightarrow \Gamma ^*$ for $i \in [1,n]$ and $\zeta \in \mathcal {L}$ by

$$\begin{aligned} \pi _{i, \zeta }(a) = \left\{ \begin{array}{ll} a \quad {\text {if con}}_{i}(\zeta , {{\,\textrm{alph}\,}}(a)) \wedge {\text {smallest}}_{i}(\zeta )\text {,}\\ 1 \quad \text {otherwise.} \end{array} \right. \end{aligned}$$

Observe that $p_i =_G \prod _{\zeta \in \mathcal {L}} \pi _{i,\zeta }(p_i)$ and each $\pi _{i, \zeta }(p_i)$ is connected.

Step 3.:

Identifying powers of single letters is obviously in $\textsf{uAC}^0$. This step does not actually replace them, instead they will be ignored during the remaining preprocessing steps and when computing the shortened word.

Step 4.:

Recall that $N = [b_1, \dots , b_{m}]$. To compute our normal form, we define the mapping $f :[1,m] \rightarrow [1,m]$ by

$$ f(i) = \min \{ j \in [1,i] \mid {{\,\textrm{alph}\,}}(b_j) = {{\,\textrm{alph}\,}}(b_i) \wedge b_i =_{G_{{{\,\textrm{alph}\,}}(b_i)}} b_j \} $$

and the mapping $\text {nfletter} :\{ b_1, \dots , b_{m} \} \rightarrow \{ b_1, \dots , b_{m} \}$ by $\text {nfletter}(b_i) = b_{f(i)}$. Then f and hence $\text {nfletter}$ can be computed in $\textsf{uAC}^0$ with oracle gates for the word problems in the base groups (resp., the uniform word problem for the class $\mathcal {C}$ in the uniform case).

Step 5a.:

By Theorem 36, we can compute a cyclic normal form in $\textsf{uAC} ^0$ with oracle gates for the word problem in $F_2$ in the non-uniform case and in $\textsf{uAC} ^0$ with oracle gates for $\textsf{NL}$ in the uniform case.

Step 5b.:

Checking for periods in words and replacing each power with a primitive factor is obviously in $\textsf{uAC} ^0$ (recall that we encode every element $\Gamma$ using the same number of bits).

Step 6.:

A cyclic normal $p'_i$ form conjugate to $p_i^{-1}$ can be computed as in step 5a. Computing all cyclic permutations of $p_i$ and $p'_i$ and selecting the lexicographically smallest one is obviously in $\textsf{uAC} ^0$.

From the complexities of the individual steps we conclude that the preprocessing can be done in $\textsf{uAC} ^0$ using oracle gates for the word problem in G and $F_2$ in the non-uniform case and in $\textsf{uAC} ^0$ using oracle gates for ${{\,\textrm{UWP}\,}}({{\,\textrm{GP}\,}}(\mathcal {C}))$ and $\textsf{NL}$ in the uniform case. $\square$

5.3.2 A Symbolic Rewriting System

We continue with a graph product of f.g. groups $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}})$. Recall the trace rewriting system $T$ from (2) in Section 2.6.5. As before, let $\sigma = |\mathcal {L}|$. From now on, we assume that $a \ne a^{-1}$ for all $a \in \Gamma$. Therefore, by Lemma 37, if $p \in M \setminus \{1\}$ is reduced, then p and $p^{-1}$ are not conjugate.

For $x \in \mathbb {Z} \setminus \{0\}$ we denote by ${{\,\textrm{sgn}\,}}x \in \{-1,1\}$ the sign of x. Moreover, let ${{\,\textrm{sgn}\,}}0 = 0$. For every $p \in \Omega$, we define the alphabet

$$\begin{aligned}&\Delta _p = \left\{ {\beta }{p^x}{\alpha } \,\vert \, \begin{matrix} x \in \mathbb {N},\\ \alpha \text{ is a prefix of } p^{\sigma } \text{ and } p \text{ is no prefix of } \alpha ,\\ \beta \text{ is a suffix of } p^{\sigma } \text{ and } p \text{ is no suffix of } \beta \end{matrix} \right\} \text{. } \end{aligned}$$

Note that a triple $(\beta ,p^x,\alpha )$ is viewed as single letter. For $(\beta ,p^x,\alpha ) \in \Delta _p$ we define $(\beta ,p^x,\alpha )^{-1} = (\alpha ^{-1},p^{-x},\beta ^{-1})$. We write $\Delta _p^{-1}$ for the set of all $(\beta ,p^x,\alpha )^{-1}$ with $(\beta ,p^x,\alpha ) \in \Delta _p$. Finally, we define the alphabet $\Delta = \Delta ' \cup \Gamma$, where $\Delta ' = \bigcup _{p \in \Omega } \Delta _p \cup \Delta _p^{-1}$. Notice that $\beta p^x\alpha$ is reduced for each $(\beta ,p^x,\alpha ) \in \Delta '$, since every $p \in \Omega$ is cyclically reduced, connected and composite.

Note that when we talk about the length of a word $w \in \Delta ^*$, every occurrence of a triple $(\beta ,p^x,\alpha ) \in \Delta '$ in w contributes by one to the length of w. To emphasize this, we write $\left| w\right| _\Delta$ for the length of a word $w \in \Delta ^*$. Moreover, $\left| w\right| _\Gamma$ (resp., $\left| w\right| _{\Delta '}$) denotes the number of occurrences of symbols from $\Gamma$ (resp., $\Delta '$) in w. In particular, $\left| w\right| _\Delta = \left| w\right| _\Gamma + \left| w\right| _{\Delta '}$ holds. Note that for $\left| w\right| _\Gamma$ the symbols from $\Gamma$ that appear within a triple $(\beta ,p^x,\alpha ) \in \Delta '$ do not contribute. For instance, if $w = ab (\beta , p^x, \alpha ) c (\delta , q^y, \gamma )$ with $a,b,c \in \Gamma$, then $\left| w\right| _\Delta = 5$, $\left| w\right| _\Gamma = 3$ and $\left| w\right| _{\Delta '} = 2$.

Lemma 46

For $(\beta ,p^x,\alpha ) \in \Delta '$ we have $|\alpha | < (\sigma - 1)|p|$ and $|\beta | < (\sigma - 1)|p|$.

Proof

By Lemma 6 we can write $\alpha = p^{k}u_1\cdots u_s$ with $s < \sigma$ where each $u_i$ is a proper prefix of p. As p is not a prefix of $\alpha$, we have $k=0$. Regarding the length of $\alpha$, we obtain $|\alpha | = \sum _{i=1}^{s} |u_i| < \sum _{i=1}^{s} |p| = s|p| \le (\sigma - 1)|p|$. The bound on the length of $\beta$ follows by symmetry. $\square$

Lemma 47

Let $(\beta ,p^x,\alpha ) \in \Delta '$.

• If a is a minimal letter of $\beta p^x \in M(\Gamma ,I)$, then there are $\beta ' \in M(\Gamma ,I)$ and $d \in \{0, {{\,\textrm{sgn}\,}}x\}$ with $(\beta ',p^{x-d},\alpha ) \in \Delta '$ and $\beta p^x =_M a \beta ' p^{x-d}$.

• If a is a maximal letter of $p^x \alpha \in M(\Gamma ,I)$, then there are $\alpha ' \in M(\Gamma ,I)$ and $d \in \{0, {{\,\textrm{sgn}\,}}x\}$ with $(\beta ,p^{x-d},\alpha ') \in \Delta '$ and $p^x \alpha =_M p^{x-d} \alpha ' a$.

Proof

We only prove the first statement, the second statement can be shown in the same way. Moreover, assume that $x \ge 0$, the case $x \le 0$ is analogous. So, assume that a is a minimal letter of the trace $\beta p^x$. The case that a is a minimal letter of $\beta$, i.e., $\beta =_M a \beta '$ for some $\beta '$, is clear. Otherwise, $x > 0$ and a must be a minimal letter of p with $(a,\beta ) \in I$. Let $\gamma \in M(\Gamma ,I)$ such that $p =_M a \gamma$. We obtain $\beta p^x =_M a \beta \gamma p^{x-1}$. It remains to show that $(\beta \gamma ,p^{x-1},\alpha ) \in \Delta '$, i.e., that $\beta \gamma$ is a suffix of $p^{\sigma }$ and p is not a suffix of $\beta \gamma$. We have $p^\sigma = u \beta$ for some $u \in M$. Moreover, p is not a suffix of $\beta$. The first statement of Lemma 6 implies that $\beta$ is a suffix of $p^{\sigma -1}$. Hence, $\beta \gamma$ is a suffix of $p^\sigma$. As $(a,\beta ) \in I$, we have $\left| \beta \right| _a = 0$. Therefore, $\left| \beta \gamma \right| _a = \left| \gamma \right| _a = \left| p\right| _a-1$. Hence, p cannot be a suffix of $\beta \gamma$. $\square$

We define the projection $\pi :\Delta ^* \rightarrow M(\Gamma ,I)$ as the unique homomorphism with $\pi (a) = a$ for $a \in \Gamma$ and $\pi ((\beta ,p^x,\alpha )) = \beta p^x \alpha$ for $(\beta ,p^x,\alpha ) \in \Delta '$. Moreover, for $a=(\beta ,p^x,\alpha )\in \Delta '$ we define ${{\,\textrm{alph}\,}}(a) = {{\,\textrm{alph}\,}}(p)\subseteq \mathcal {L}$ (and ${{\,\textrm{alph}\,}}(a)$ as defined before for $a\in \Gamma$). Now, we can define an independence relation $I_\Delta$ on $\Delta$ by setting $(t,u) \in I_\Delta$ if and only if ${{\,\textrm{alph}\,}}(t)\times {{\,\textrm{alph}\,}}(u) \subseteq I$. Notice that, if $t, u \in \Delta$ are not of the form $(\beta ,p^x,\alpha )$ with $x=0$, then $(t,u) \in I_\Delta$ iff $(\pi (u),\pi (t)) \in I$; for elements of the form $(\beta ,p^0,\alpha )$, however, this is not an equivalence.

Let us consider the corresponding trace monoid $M(\Delta , I_\Delta )$: it contains $M(\Gamma ,I)$ and $\pi$ defines a surjective homomorphism $M(\Delta , I_\Delta ) \rightarrow M(\Gamma ,I)$, which we denote by the same letter $\pi$. We define a trace rewriting system $R$ over $M(\Delta , I_\Delta )$ by the rules given in Table 1.

Table 1 The rules for the rewriting system $R$

Remark 48

To understand rules (2) and (3) in Table 1 one has to apply Lemma 14 to the traces $p^x \alpha$, $\pi (u)$, and $q^y \delta$ (where $p=q$ might hold). Note that $p^x \alpha \pi (u), \pi (u)\delta q^y \in {{\,\textrm{IRR}\,}}(T)$. If $p^x \alpha \pi (u) \delta q^y \notin {{\,\textrm{IRR}\,}}(T)$ then Lemma 14 tells us there must exist a prefix s of $p^x\alpha$, a suffix t of $\delta q^y$, and an I-clique v such that

$$ p^x\alpha \, \pi (u) \,\delta q^y \ \overset{*}{\underset{T}{\Longrightarrow }}\ s \, v \, \pi (u) \, t $$

and $(\pi (u),v) \in I$. Moreover, by Lemma 47 we can write s and t as $p^{x'} \alpha '$ and $\delta ' q^{y'}$, respectively, where $x' \in \llbracket x \rrbracket$, $y' \in \llbracket y \rrbracket$, and $(\beta ,p^{x'},\alpha '), (\delta ',q^{y'},\gamma ) \in \Delta '$.

Remark 49

In rules (2) and (3) we allow u to contain a minimal letter a such that $(p,a) \in I$. Similarly, u may contain a maximal letter b such that $(b,p) \in I$ in rule (2) and $(b, q) \in I$ in rule (3). On the other hand, we could forbid this situation and require that $(\beta , p^x,\alpha )$ is the only minimal letter of the left-hand sides of rules (2) and (3) (and similarly for the maximal letters). This would not change the arguments in our further considerations.

The following facts about $R$ are crucial.

Lemma 50

For $u, v \in M(\Delta , I_\Delta )$ we have

• 1. $\pi ({{\,\textrm{IRR}\,}}(R)) \subseteq {{\,\textrm{IRR}\,}}(T)$,

• 2. $u \overset{*}{\underset{R}{\Longrightarrow }} v$ implies $\pi (u) \overset{*}{\underset{T}{\Longrightarrow }} \pi (v)$,

• 3. R is terminating,

• 4. $\pi (u) =_G 1$ if and only if $u \overset{*}{\underset{R}{\Longrightarrow }} 1$.

Proof

We start with statement 1. Assume we have an element $t \in {{\,\textrm{IRR}\,}}(R)$ with $\pi (t) \notin {{\,\textrm{IRR}\,}}(T)$. So, none of the rules of $R$ can be applied to t. For rule (4) this implies that $x \ne 0$ for every $(\beta ,p^x,\alpha ) \in \Delta '$ that occurs in t. Since $\pi (t) \notin {{\,\textrm{IRR}\,}}(T)$, there is a factor ab in $\pi (t)$ with $a, b \in \Gamma$ and ${{\,\textrm{alph}\,}}(a) = {{\,\textrm{alph}\,}}(b)$. We have $ab \overset{\Longrightarrow }{T}\ [ab]$ (we may have $[ab]=1$). Let $t = t_1 t_2 \cdots t_m$ with $t_i \in \Delta$. As every $\pi (t_i) \in M(\Gamma ,I)$ is reduced with respect to $T$, a and b must be located in different factors $\pi (t_i)$. Assume that a belongs to $\pi (t_i)$ and b belongs to $\pi (t_j)$ for some $j > i$ (note that $j< i$ is not possible since $(a,b) \in D$). Let $u = t_{i+1}\cdots t_{j-1}$ (which might be empty). It follows that a is a maximal letter of $\pi (t_i)$, b is a minimal letter of $\pi (t_j)$, $(\pi (u),a)\in I$ and $(\pi (u),b)\in I$. Moreover, we can assume that i and j are chosen such that $j-i$ is minimal, which implies that $\pi (u t_j), \pi (t_i u) \in {{\,\textrm{IRR}\,}}(T)$.

If $t_i$ and $t_j$ are both in $\Gamma$, then rule (7) can be applied, which is a contradiction. If $t_i = (\beta ,p^x,\alpha ) \in \Delta '$ and $t_j = b \in \Gamma$, then a must be a maximal letter of $p^x \alpha$ (since $x \ne 0$). Hence, by Lemma 47, rule (6) can be applied. Similarly, if $t_i \in \Gamma$ and $t_j \in \Delta '$ then rule (5) can be applied. In both cases we obtain a contradiction. Finally, if $t_i, t_j \in \Delta '$, the situation is a bit more subtle. Assume that $t_i = (\beta ,p^x,\alpha )$ and $t_j = (\delta ,q^y,\gamma )$ for $x \ne 0 \ne y$. Clearly, a is a maximal letter of $p^x\alpha$, and b is a minimal letter of $\delta q^y$. Moreover, $p^x \alpha \pi (u), \pi (u) \delta q^y \in {{\,\textrm{IRR}\,}}(T)$. Our consideration from Remark 48 shows that

$$ p^x\alpha \, \pi (u) \,\delta q^y \overset{+}{\underset{T}{\Longrightarrow }} p^{x'} \alpha ' \, v \pi (u) \, \delta ' q^{y'} \in {{\,\textrm{IRR}\,}}(T) $$

for some I-clique v with $(\pi (u),v) \in I$, $x' \in \llbracket x \rrbracket$, $y' \in \llbracket y \rrbracket$, and $\alpha ', \delta '$ with $(\beta ,p^{x'},\alpha '), (\delta ',q^{y'},\gamma ) \in \Delta '$. If $p \ne q$ then rule (3) can be applied to t. On the other hand, if $p = q$ then, rule (1) or (2) can be applied. Altogether, it follows that one of the rules of $R$ can be applied contradicting $t \in {{\,\textrm{IRR}\,}}(R)$. Thus $\pi ({{\,\textrm{IRR}\,}}(R)) \subseteq {{\,\textrm{IRR}\,}}(T)$.

For statement 2 observe that the rules of $R$ only allow such reductions that are also allowed in T. To see statement 3, consider a rewriting step $u \overset{\Longrightarrow }{R}\ v$. This means that we have $u \overset{*}{\underset{T}{\Longrightarrow }} v$ and either $|u|_{\Delta '} > |v|_{\Delta '}$ (for rules (1) and (4)) or $u \overset{+}{\underset{T}{\Longrightarrow }} v$ and $|u|_{\Delta '} = |v|_{\Delta '}$ (for the other rules). Hence, as T is terminating, so is R (indeed, in Lemma 53 below, we give explicit bounds on the number of possible rewriting steps).

Statement 4 follows from statements 1 and 2. If $u \overset{*}{\underset{R}{\Longrightarrow }} 1$, then $\pi (u) \overset{*}{\underset{T}{\Longrightarrow }} 1$ by statement2, i.e., $\pi (v) =_G 1$. On the other hand, if $u \overset{*}{\underset{R}{\Longrightarrow }} 1$ does not hold, then, since $R$ is terminating, there exists $v \in {{\,\textrm{IRR}\,}}(R)$ with $u \overset{*}{\underset{R}{\Longrightarrow }} v\ne 1$. We obtain $\pi (u) \overset{*}{\underset{T}{\Longrightarrow }} \pi (v) \ne 1$ by statement 2 and $\pi (v) \in {{\,\textrm{IRR}\,}}(T)$ by statement 1. Since $T$ is terminating and confluent this implies $\pi (u) =_G \pi (v) \ne _G 1$. $\square$

Lemma 51

The following length bounds hold:

• Rule (1): $\left| f\right| \le 2\sigma$

• Rule (2): $|d| \le 5\sigma$ and $|e| \le 5\sigma$

• Rule (3): $|d| \le 4\sigma |q|$ and $|e| \le 4\sigma |p|$

• Rule (4): $|\beta \alpha | < 2(\sigma - 1)|p|$

• Rules (5) and (6): $|d| \le 1$

Remark 52

Note that the proof of the bound for rule (2) in Lemma 51 essentially relies on the assumption $a\ne a^{-1}$ for $a\in \Gamma$. Indeed, without this requirement we can construct examples where d and e in rule (2) can be arbitrarily large. In the corresponding [58, 59, Lemma 15], there is the unfortunate mistake that this condition is not required. Notice that the correctness of the whole shortening process described below depends on the bounds provided by Lemma 51. Moreover, Lemma 51 is the only place in our construction for the power word problem in graph products where we explicitly use the requirement $a\ne a^{-1}$ for $a\in \Gamma$.

Proof of Lemma

51 We look at the individual statements: Rule (1): The bound on $\left| f\right|$ is trivial since $\left| \alpha \right| , \left| \beta \right| \le \sigma \left| p\right|$.

Rule (2): Let $\iota = {{\,\textrm{sgn}\,}}x$ and $\kappa = {{\,\textrm{sgn}\,}}y$. We distinguish two cases. First, assume that $(p, \pi (u)) \in I$. Then, due to condition (1), $\alpha \delta$ does not reduce with T to a power of p. Most importantly, we have $\alpha \delta \ne _G 1$.

We apply Lemma 14 (with $q=1$) to the reduced traces $p^x \alpha$ and $\delta p^y$. Due to the form of rule (2) we obtain factorizations $p^x \alpha =_M p^{x-d} \alpha ' rs$ and $\delta p^y =_M s^{-1}t \delta ' p^{y-d}$ such that r and t are I-cliques with $rt \overset{*}{\underset{T}{\Longrightarrow }} v$ for an I-clique v with ${{\,\textrm{alph}\,}}(r) = {{\,\textrm{alph}\,}}(t) = {{\,\textrm{alph}\,}}(v)$ and s is a suffix of $p^{x}\alpha$ and $s^{-1}$ is a prefix of $\delta p^{y}$. Moreover, we can assume that $p^\iota$ is not a prefix of $\alpha '$ and $p^\kappa$ is not a suffix of $\delta '$.

Assume that $\left| s\right| \ge 3 \sigma \left| p\right|$. We will deduce a contradiction. Since $\left| \alpha \right| , \left| \delta \right| \le \sigma \left| p\right|$, this implies $\left| y\right| ,\left| x \right| \ge 2\sigma$ and (by Lemma 6) s has a suffix $p^{\iota \sigma } \alpha$. Since $s^{-1}$ is a prefix of $\delta p^y$, it follows that $p^{\iota \sigma } \alpha$ is a suffix of $p^{-y} \delta ^{-1}$. Hence, there is a trace q with

$$\begin{aligned} q p^{\iota \sigma } \alpha =_M p^{-y} \delta ^{-1}. \end{aligned}$$

(7)

First, consider the case $\iota = \kappa$. As $\delta$ is a suffix of $p^{\kappa \sigma }$, there is some $q'$ with $\delta ^{-1} q' =_M p^{-\kappa \sigma }$. Hence, by (7), we have $q p^{\iota \sigma } \alpha q' =_M p^{-y-\kappa \sigma } =_M (p^{-\iota })^{|y|+\sigma }$. As the number of letters from each $\zeta \in \mathcal {L}$ is the same in p and $p^{-1}$, Lemma 9 implies that p is conjugate to $p^{-1}$. But since p and $p^{-1}$ are both reduced this contradicts Lemma 37. Be aware that here we rely upon the assumption $a \ne a^{-1}$ for all $a \in \Gamma$.

Now consider the case $\iota \ne \kappa$. For simplicity, assume $\iota =1$ and $\kappa = -1$ (the other case works exactly the same way), i. e., $y \le -2\sigma$. Recall that $\alpha$ is a prefix $p^\sigma$. With (7) we obtain $q p^\sigma \alpha =_M p^{-y} \delta ^{-1} =_M p^{\sigma } p^{-y-\sigma } \delta ^{-1}$, where $\alpha$ is a prefix of $p^{-y-\sigma }$. It follows that $\alpha$ must be a suffix of $p^{-y-\sigma } \delta ^{-1}$. Hence, there exists $q''$ such that $p^{-y} \delta ^{-1} =_M q p^\sigma \alpha =_M p^{\sigma } q''\alpha$ and therefore $q p^\sigma =_M p^{\sigma } q''$. Note that $p^{-y} \delta ^{-1}$ is a prefix of some $p^z$ with $z \in \mathbb {N}$. In particular, there is some $z \ge \sigma$ such that $p^{\sigma } q''\alpha$ is a prefix of $p^z$. It follows that $q''$ is a prefix of some $p^k$ with $k \in \mathbb {N}$. Since $p \in \Omega$ is connected and primitive as a trace, Lemma 8 implies that $q=q''=p^\ell$ for some $\ell \in \mathbb {N}$. We obtain $p^{-y} \delta ^{-1} =_M p^{\sigma +\ell } \alpha$ and hence $\alpha \delta =_G p^{j}$ for some $j\in \mathbb {Z}$ (indeed, as $p^{-1}$ is not a suffix of $\delta$ and p is not a prefix of $\alpha$, it follows that $\alpha \delta =_G 1$). Again, we obtained a contradiction.

Hence, in both cases it follows that $\left| s\right| < 3 \sigma \left| p\right|$. As above, we write $p^d \alpha =_M \alpha ' r s$. By Lemma 46, we have $|\alpha '| < (\sigma - 1)|p|$. Moreover, as r is an I-clique, $\left| r\right| \le \sigma$. It follows that

$$\begin{aligned} d|p| \le |p^d| + |\alpha | = |\alpha '| + |r| + |s| \le (\sigma - 1) |p| + \sigma + 3\sigma |p|. \end{aligned}$$

Hence, we obtain $d \le 5\sigma$. The bound on |e| follows by symmetry.

Now assume that $(p, \pi (u)) \notin I$. Let $\alpha ''$ be the suffix of $p^x\alpha$ and $\delta ''$ be the prefix of $\delta p^y$ such that $\alpha '' \pi (u) \delta '' \overset{*}{\underset{T}{\Longrightarrow }} v \pi (u)$ for an I-clique v. By Lemma 14, $\alpha ''$ and $\delta ''$ must commute with $\pi (u)$. Thus, $p^{\iota }$ cannot be a factor of $\alpha ''$ and hence, by Lemma 6, $\alpha ''$ must be a suffix of $p^{(\sigma - 1)\iota }\alpha$. Thus $|d| \le \sigma - 1 < 5\sigma$. The bound on |e| follows by symmetry.

Rule (3): By Lemma 14 we obtain factorizations $p^x \alpha =_M p^{x-d} \alpha ' rs$ and $\delta q^y =_M s^{-1}t \delta ' p^{y-e}$ such that r and t are I-cliques with $rt \overset{*}{\underset{T}{\Longrightarrow }} v$ for the I-clique v with ${{\,\textrm{alph}\,}}(r) = {{\,\textrm{alph}\,}}(t) = {{\,\textrm{alph}\,}}(v)$ and $(rs, \pi (u)) \in I$. Thus, we can write $p^d\alpha = \alpha 'rs$ and $\delta q^e = s^{-1} t \delta '$. Moreover, s is a factor of $p^{{{\,\textrm{sgn}\,}}(x)\nu }$ and $s^{-1}$ is a factor of $q^{{{\,\textrm{sgn}\,}}(y)\nu }$ for some large enough $\nu \in \mathbb {N}$. We have $|s| \le 2\sigma (|p| + |q|)$. Otherwise, we would have $p = q$ by Theorem 42 contradicting $p \ne q$. By Lemma 46, $|\alpha '| < (\sigma - 1)|p|$ and $|\delta '| < (\sigma - 1)|q|$. It follows that

$$\begin{aligned} |p^d\alpha |&= |\alpha 'rs| = |\alpha '| + |r| + |s| \\&< 2\sigma (|p| + |q|) + \sigma + (\sigma - 1)|p| \\&< 4\sigma (|p| + |q|) \\&\le 4\sigma |p| |q|. \end{aligned}$$

For the last inequality note that $p, q \in \Omega$ are composite. We get $|d|\cdot |p| \le |p^d\alpha | \le 4\sigma |p| |q|$, i.e., $|d| < 4\sigma |q|$. By symmetry, it follows that $|e| < 4\sigma |p|$.

Rule (4): By Lemma 46, $|\alpha | < (\sigma - 1) |p|$ and $|\beta | < (\sigma - 1) |p|$.

Rule (5): There is a single letter prefix b of $\beta p^x$ with ${{\,\textrm{alph}\,}}(a) = {{\,\textrm{alph}\,}}(b)$. Either b is a prefix of $\beta$ in which case $d = 0$ or, if it is not, then b must be a prefix of $p^{{{\,\textrm{sgn}\,}}x}$ in which case $|d| = 1$. The same bound on rule (6) follows by symmetry. $\square$

For a trace $w = w_1\cdots w_n \in M(\Delta , I_\Delta )$ with $w_i \in \Delta$, we define

$$\begin{aligned} \mu (w)&= \max \left\{ |p| \mid w_i = (\beta ,p^x,\alpha ) \in \Delta ',\, i \in [1,n] \right\} . \end{aligned}$$

For convenience we define $\mu (w)=2$ if w does not contain any letter from $\Delta '$. The reason behind this is that $|p| \ge 2$ for all $(\beta ,p^x,\alpha ) \in \Delta '$ as $p \in \Omega$ is required to be composite. Thus, in any case we have $\mu (w) \ge 2$.

Lemma 53

If $w \overset{*}{\underset{R}{\Longrightarrow }} v$, then $w \overset{\le k}{\underset{R}{\Longrightarrow }} v$ with $k = 10\sigma ^2 |w|_\Delta ^2\mu (w)$.

Proof

We observe the following bounds on the number of applications of the individual rules of the rewriting system (which we will prove below):

• 1. Rules (1) and (4) can be applied at most $|w|_{\Delta '}$ times in total.

• 2. Rules (2) and (3) can be applied at most $2\sigma |w|_{\Delta '}$ times.

• 3. Rule (7 and length-reducing applications of rules (5) and (6) can occur at most $|w|_{\Gamma } + 2|w|_{\Delta '}(\sigma ^2 + (\sigma -1)\mu (w))$ times.

• 4. Length-preserving applications of rules (5) and (6) can occur at most $|w|_{\Gamma }|w|_{\Delta '} + 2|w|_{\Delta '}^2(\sigma ^2 + (\sigma -1)\mu (w))$ times.

Adding up those bounds we obtain a bound of

$$\begin{aligned} (2 \sigma + 1)|w|_{\Delta '}&+ (|w|_{\Delta '} + 1) \bigl (|w|_{\Gamma } + 2|w|_{\Delta '}(\sigma ^2 + (\sigma -1)\mu (w))\bigr )\\&\le 10\sigma ^2 |w|_\Delta ^2\mu (w). \end{aligned}$$

Thus, let us prove the individual bounds 1–4.

• 1. For an application $w \underset{R}{\Longrightarrow }\ \tilde{w}$ of rule (1) or (4) we have $|w|_{\Delta '} > |\tilde{w}|_{\Delta '}$. Moreover, no rule increases $|w|_{\Delta '}$.

• 2. For bounding the number of applications of rules (2) and (3), write $w=_Mw_1 \cdots w_n$ with $w_i \in \Delta$. We say that a pair (i, j) with $1 \le i < j \le n$ potentially cancels if $w_i,w_j \in \Delta '$ and there is some $\zeta \in \mathcal {L}$ such that $\zeta \in {{\,\textrm{alph}\,}}(w_i) \cap {{\,\textrm{alph}\,}}(w_j)$ and for all $i<k<j$ either $w_k \in \Gamma$ or $w_k \in \Delta '$ with $\zeta \not \in {{\,\textrm{alph}\,}}(w_k)$. Notice that the number of pairs that potentially cancel does not depend on the representative $w_1 \cdots w_n$ we started with (as the letters from $\Gamma _\zeta$ are linearly ordered). Moreover, if a rule (2) or (3) can be applied at positions $i < j$ in w, then there must be letters a in $\pi (w_i)$ and b in $\pi (w_j)$ from the same alphabet $\Gamma _\zeta$ (in particular, $\zeta \in {{\,\textrm{alph}\,}}(w_i) \cap {{\,\textrm{alph}\,}}(w_j)$) such that $(a, w_k) \in I_\Delta$ for all $i< k < j$. Therefore, (i, j) potentially cancels – the converse, however, does not hold. Furthermore, for each pair that potentially cancels (at some point during the rewriting process $w \overset{*}{\underset{R}{\Longrightarrow }} v$), a rule of type (2) or (3) can be applied at most once. This is because the right-hand side of the rule is in $\pi ^{-1}({{\,\textrm{IRR}\,}}(T))$ and irreducibility is not changed by the application of other rules (indeed, not by any application of rules from T). Thus, it suffices to bound the number of pairs that potentially cancel. Initially, for each position i with $w_i\in \Delta '$ there are at most $\sigma$ positions $j>i$ such that (i, j) potentially cancels as well as at most $\sigma$ positions $j<i$ such that (j, i) potentially cancels. Hence, initially there are at most $\sigma |w|_{\Delta '}$ pairs that potentially cancel. Each removal of a letter from $\Delta '$ by rule (4) might generate up to $\sigma$ pairs that potentially cancel. All other rules do not generate pairs that potentially cancel. Thus, in the entire rewriting process only $2\sigma |w|_{\Delta '}$ pairs potentially cancel, which gives us an upper bound of at most $2\sigma |w|_{\Delta '}$ applications of rules (2) and (3).

• 3. Initially, there are $|w|_{\Gamma }$ letters from $\Gamma$. Each application of rules (2) or (3) increases $|\cdot |_{\Gamma }$ by up to $\sigma$ (since $\left| v\right| \le \sigma$). Each application of rule (4) increases $|\cdot |_{\Gamma }$ by up to $2(\sigma - 1)\mu (w)$. Rule (7) as well as length-reducing applications of rules (5) and (6) decrease $|\cdot |_{\Gamma }$ by at least one. Therefore, in total they can occur at most $|w|_{\Gamma } + \sigma \cdot 2\sigma |w|_{\Delta '} + 2(\sigma - 1)\mu (w) \cdot |w|_{\Delta '} = |w|_{\Gamma } + 2|w|_{\Delta '}(\sigma ^2 + (\sigma -1)\mu (w))$ times.

• 4. A length-preserving application of rule (5) or (6) involves a letter from $\Delta '$ and a letter from $\Gamma$. Moreover, for each such pair of letters, a rule (5) or (6) can be applied at most once. There are $|w|_{\Gamma }$ letters from $\Gamma$ initially. Up to $2|w|_{\Delta '}(\sigma ^2 + (\sigma -1)\mu (w))$ additional letters from $\Gamma$ are created by rules (2), (3) and (4) (see point 3). Multiplying that with $|w|_{\Delta '}$, the number of letters from $\Delta '$, we obtain a bound of $|w|_{\Gamma }|w|_{\Delta '} + 2|w|_{\Delta '}^2(\sigma ^2 + (\sigma -1)\mu (w))$ for the number of length-preserving applications of rules (5) and (6). $\square$

5.3.3 The Shortened Word

In this section we describe the shortening process. It is almost the same as for free groups as we presented it in [43] (see the version on arXiv [42] for details). For further consideration we fix a trace $u \in M(\Delta ,I_\Delta )$ and some $p \in \Omega$. We consider all letters from $\Delta _p \cup \Delta _p^{-1}$ in u and write u as

$$\begin{aligned} u = u_0\, (\beta _1,p^{y_1},\alpha _1)\, u_1 \cdots (\beta _m,p^{y_m},\alpha _m)\, u_m \end{aligned}$$

(8)

with $u_i \in M(\Delta ,I_\Delta )$ not containing any letter from $\Delta _p \cup \Delta _p^{-1}$ and $(\beta _i ,p^{y_i},\alpha _i) \in \Delta _p \cup \Delta _p^{-1}$. We define $\eta _p(u) = \sum _{j=1}^m y_j$ and $\eta _p^i(u) = \sum _{j=1}^i y_j$ for $i \in [0,m]$. The following lemma follows from the bounds given in Lemma 51.

Lemma 54

Let $u, v \in M(\Delta ,I_\Delta )$ and $u \overset{\Longrightarrow }{R}\ v$. For every prefix $v'$ of v there is a prefix $u'$ of u such that for all $p \in \Omega$

$$\begin{aligned} |\eta _p(u') - \eta _p(v')| \le 5\sigma \mu (u). \end{aligned}$$

If the applied rule is neither (1) nor (4), then for all $p \in \Omega$ and $i \in [0, m]$ we have

$$\begin{aligned} |\eta _p^i(u) - \eta _p^i(v)| \le 5\sigma \mu (u). \end{aligned}$$

Proof

Let us start by proving the second statement. First, observe that in case the applied rule is neither (1) nor (4), there is a one-to-one correspondence between letters from $\Delta _p \cup \Delta _p^{-1}$ in u and v. Moreover, when applying a rule other than (1) or (4), at most two letters from $\Delta _p \cup \Delta _p^{-1}$ are modified; when also excluding rule (2) at most one letter from $\Delta _p \cup \Delta _p^{-1}$ is modified. Therefore, by Lemma 51, in case of rule (2), we have $|\eta _p^i(u) - \eta _p^i(v)| \le 10\sigma \le 5\sigma \mu (u)$ (because $\mu (u) \ge 2$). In case of rules (3) or (5)–(7), also by Lemma 51, it follows that $|\eta _p^i(u) - \eta _p^i(v)| \le 4\sigma \mu (u)$.

Now, observe that the second statement implies the first one in the case that the applied rule is neither (1) nor (4): if $v'$ is a prefix of v containing exactly the first i letters from $\Delta _p \cup \Delta _p^{-1}$, then we can choose $u'$ to be any prefix of u containing exactly the first i letters from $\Delta _p \cup \Delta _p^{-1}$.

Now, suppose that the applied rule is (4). Then we have $\eta _p(u) = \eta _p(v)$; moreover, for a prefix $v'$ of v it is clear that we can find a corresponding prefix $u'$ of u with $\eta _p(u') = \eta _p(v')$.

Finally, consider the case of rule (1) and denote the applied rule by $\ell \rightarrow r$. Note that r is a word of length one. Thus, r is either completely outside of $v'$ or completely inside of $v'$. In the first case, we can choose $u' = v'$. In the second case, we can write $v' = srt$ and set $u' = s\ell t$. Lemma 51 yields $|\eta _p(u') - \eta _p(v')| \le 2\sigma$. $\square$

In the following we define a set $\mathcal {C}$ of intervals to be carved out of the exponents from the input power word during the shortening process.

Definition 55

Let $\mathcal {C} = \left\{ [l_j, r_j] \mid j \in [1,k] \right\}$ with $l_j,r_j \in \mathbb {Z}$ be a set of finite, non-empty, and pairwise disjoint intervals of integers, where $k = |\mathcal {C}|$. We assume the intervals to be ordered, i. e., $r_j < l_{j+1}$. We define the size of an interval $d_j = r_j - l_j + 1$ (which is the number of elements in $[l_j, r_j]$). An element $u \in M(\Delta ,I_\Delta )$ (written in the form (8)) is said to be compatible with the set of intervals $\mathcal {C}$, if for every prefix $u'$ of u and all $j \in [1,k]$, we have $\eta _p(u') \notin [l_j, r_j]$.

Definition 56

Let $\mathcal {C} = \left\{ [l_j, r_j] \mid j \in [1,k] \right\}$ be compatible with $u \in M(\Delta ,I_\Delta )$ written in the form (8). The shortened word corresponding to u is

$$\begin{aligned} \mathcal {S}_{\mathcal {C}}(u) = u_0 (\beta _1,p^{z_1},\alpha _1) u_1 \cdots (\beta _m,p^{z_m},\alpha _m)u_m. \end{aligned}$$

The new exponents $z_i$ are defined as

$$\begin{aligned} z_i = y_i - {{\,\textrm{sgn}\,}}(y_i)\cdot \sum _{j \in C_i(u)} d_j\text {,} \end{aligned}$$

where $C_i(u)$ is the set of indices of intervals to be removed from $y_i$, defined by

$$\begin{aligned} C_i(u) = \left\{ \begin{matrix} \{ j \in [1,k] \eta _p^{i-1}(u)< l_j \le r_j< \eta _p^i(u) \} &{}\quad \text { if } y_i > 0,\\ \{ j \in [1,k] \eta _p^{i}(u)< l_j \le r_j< \eta _p^{i-1}(u)\} &{}\quad \text { if } y_i < 0. \end{matrix} \right. \end{aligned}$$

Note that Definitions 55 and 56 depend on our fixed $p \in \Omega$.

Lemma 57

If $u \in {{\,\textrm{IRR}\,}}(R)$, then $\mathcal {S}_{\mathcal {C}}(u) \in {{\,\textrm{IRR}\,}}(R)$.

Proof

Assume that $u \in {{\,\textrm{IRR}\,}}(R)$. In particular, $y_i \ne 0$ for all $i \in [1,m]$ (otherwise we could apply rule (4)). We prove the lemma by showing that ${{\,\textrm{sgn}\,}}(y_i) = {{\,\textrm{sgn}\,}}(z_i)$ and $z_i \ne 0$ for all $i \in [1,m]$. As the intervals in $\mathcal {C}$ are ordered, there are $\iota$ and $\tau$ such that $C_i(u)$ consists of all indices from $\iota$ to $\tau$. In case $y_i > 0$ we have

$$\begin{aligned} z_i&= y_i - \sum _{j \in C_i(u)} d_j\\&= y_i - \sum _{j = \iota }^\tau d_j\\&= y_i - \sum _{j = \iota }^\tau (r_j - l_j + 1)\\&\ge y_i - (r_{\tau } - l_{\iota } + 1)\qquad \qquad \qquad {(\text {because} r_j < l_{j+1})}\\&\ge y_i - \bigl ((\eta _p^i(u) - 1) - (\eta _p^{i-1}(u) + 1) + 1\bigr )\\&= y_i - y_i + 1\\&= 1 . \end{aligned}$$

The case $y_i < 0$ follows by symmetry. $\square$

Definition 58

We define the distance between some u and the closest interval from $\mathcal {C}$ as

$$\begin{aligned} {{\,\textrm{dist}\,}}_p(u, \mathcal {C}) = \min \big \{ | \eta _p^i(u) - x | \; \big \vert ~i \in [0,m],\, x \in [l, r] \in \mathcal {C} \big \}. \end{aligned}$$

From that definition the following statement follows immediately.

Lemma 59

${{\,\textrm{dist}\,}}_p(u, \mathcal {C}) > 0$ if and only if u is compatible with $\mathcal {C}$.

We want to show that under certain conditions, any rewriting step that is possible on u is also possible on $\mathcal {S}_{\mathcal {C}}(u)$.

Lemma 60

If ${{\,\textrm{dist}\,}}_p(u, \mathcal {C}) > 5\sigma \mu (u)$ and $u \underset{R}{\Longrightarrow }\ v$, then $\mathcal {S}_{\mathcal {C}}(u) \underset{R}{\Longrightarrow }\ \mathcal {S}_{\mathcal {C}}(v)$.

Proof

Observe that u is compatible with $\mathcal {C}$. By Lemma 54 we have ${{\,\textrm{dist}\,}}_p(v, \mathcal {C}) > 0$ and thus v is compatible with $\mathcal {C}$. It follows that $\mathcal {S}_{\mathcal {C}}(u)$ and $\mathcal {S}_{\mathcal {C}}(v)$ are defined.

To prove the lemma, we compare the shortened version of u and v and show that a rule from $R$ can be applied. We distinguish which rule from $R$ has been applied in the rewrite step $u \underset{R}{\Longrightarrow }\ v$.

Rule (2), (3), (5), (6) or (7): If one of these rules has been applied, the shortening process has the same effect on u and v, i. e., $C_i(u) = C_i(v)$ for all i (this is because by Lemma 54 we have $|\eta _p^i(u) - \eta _p^i(v)| \le 5\sigma \mu (u)$ and the assumption ${{\,\textrm{dist}\,}}_p(u, \mathcal {C}) > 5\sigma \mu (u)$). The same rule that has been applied in $u \underset{R}{\Longrightarrow }\ v$ can also be used to get $\mathcal {S}_{\mathcal {C}}(u) \underset{R}{\Longrightarrow }\ \mathcal {S}_{\mathcal {C}}(v)$: Consider a letter $(\beta ,p^{y_i},\alpha )$ in u that by the shortening process is changed to $(\beta ,p^{z_i},\alpha )$ with $z_i\ne y_i$. Then $C_i(u) \ne \emptyset$ and we have

$$\begin{aligned} \left| z_i \right| = \left| y_i \right| - \sum _{j\in C_i(u)} d_j \ge 2{{\,\textrm{dist}\,}}_p(u, \mathcal {C}) \ge 5\sigma \mu (u). \end{aligned}$$

Thus, by Lemma 51 the exponents in $\mathcal {S}_{\mathcal {C}}(u)$ are large enough to apply a rule of the same type as in $u \underset{R}{\Longrightarrow }\ v$.

Rule (4): If rule (4) is applied, then $C_\ell (v) = C_\ell (u)$ for $\ell < i$ and $C_\ell (v) = C_{\ell + 1}(u)$ for $\ell \ge i$. We also know $y_i = 0$, which is not altered by the shortening process, i. e., $C_i(u) = \emptyset$. Thus, rule (4) can be applied to $\mathcal {S}_{\mathcal {C}}(u)$ to obtain $\mathcal {S}_{\mathcal {C}}(v)$.

Rule (1): Finally, consider the case that rule (1) has been applied. Let

$$\begin{aligned} u = u_0 (\beta _1,p^{y_1},\alpha _1) u_1 \cdots (\beta _i,p^{y_i},\alpha _i)\, u_i \,(\beta _{i+1},p^{y_{i+1}},\alpha _{i+1})\, u_{i+1} \cdots (\beta _m,p^{y_m},\alpha _m) u_m. \end{aligned}$$

The result of applying the rule is

$$\begin{aligned} v = u_0 (\beta _1,p^{y_1},\alpha _1) u_1 \cdots (\beta _i,p^{y_i + y_{i+1} + f}, \alpha _{i+1}) \, u_i u_{i+1} \cdots (\beta _m,p^{y_m},\alpha _m) u_m \end{aligned}$$

where $\alpha _i\beta _{i+1} =_G p^f$ (notice that $(u_i,p) \in I_\Delta$, for otherwise rule (1) cannot be applied). On powers not modified by the rule the shortening process behaves the same on u and v, i. e., $C_\ell (v) = C_\ell (u)$ for $\ell < i$ and $C_\ell (v) = C_{\ell + 1}(u)$ for $\ell > i$ (because by Lemma 51, $|f| \le 2\sigma < {{\,\textrm{dist}\,}}_p(u, \mathcal {C})$). The result of the shortening process on v is

$$\begin{aligned} \mathcal {S}_{\mathcal {C}}(v) = u_0 (\beta _1,p^{z_1},\alpha _1) u_1 \cdots (\beta _i,p^{\tilde{z}_i},\alpha _{i+1}) u_i u_{i+1} \cdots (\beta _m,p^{z_{m}},\alpha _m) u_m\text {,} \end{aligned}$$

where $\tilde{z}_i = y_i + y_{i+1} + f- {{\,\textrm{sgn}\,}}(y_i + y_{i+1} + f) \cdot \sum _{\ell \in C_i(v)} d_\ell$. Rule (1) can be also applied to $\mathcal {S}_{\mathcal {C}}(u)$ (only $\alpha _i\beta _{i+1} =_G p^f$ is needed for this) and yields

$$\begin{aligned} \hat{v} = u_0 (\beta _1,p^{z_1},\alpha _1) u_1 \cdots (\beta _i,p^{z_i + z_{i+1} + f},\alpha _{i+1}) u_i u_{i+1} \cdots (\beta _m,p^{z_{m}},\alpha _m) u_m. \end{aligned}$$

We need to show that $\tilde{z}_i = z_i + z_{i+1} + f$, i. e.,

$$z_i + z_{i+1} = y_i + y_{i+1} - {{\,\textrm{sgn}\,}}(y_i + y_{i+1} + f) \cdot \sum _{\ell \in C_i(v)} d_\ell .$$

We start by showing that, if $C_i(v) \ne \emptyset$, then ${{\,\textrm{sgn}\,}}(y_i + y_{i+1} + f) = {{\,\textrm{sgn}\,}}(y_i + y_{i+1})$. Indeed, if $j\in C_i(v)$, then for all $x \in [l_j,r_j]$ we have

$$\left| y_i + y_{i+1} + f \right| \ge \big |\eta _p^{i-1}(v)-x\big | = \big |\eta _p^{i-1}(u)-x\big | \ge {{\,\textrm{dist}\,}}_p(u, \mathcal {C}) .$$

The last inequality follows from $[l_j,r_j ] \in \mathcal {C}$. Since, by Lemma 51, $|f| \le 2\sigma < {{\,\textrm{dist}\,}}_p(u, \mathcal {C})$, it follows that ${{\,\textrm{sgn}\,}}(y_i + y_{i+1} + f) = {{\,\textrm{sgn}\,}}(y_i + y_{i+1})$.

Therefore, in any case we have

$${{\,\textrm{sgn}\,}}(y_i + y_{i+1}) \cdot \!\sum _{\ell \in C_i(v)} d_\ell = {{\,\textrm{sgn}\,}}(y_i + y_{i+1} + f) \cdot \!\sum _{\ell \in C_i(v)} d_\ell $$

and it remains to show $z_i + z_{i+1} = y_i + y_{i+1} - {{\,\textrm{sgn}\,}}(y_i + y_{i+1}) \cdot \sum _{\ell \in C_i(v)} d_\ell$.

Now let us distinguish two cases: First, consider the case that $y_i$ and $y_{i+1}$ have the same sign. In that case we have $C_i(u) \cap C_{i+1}(u) = \emptyset$ and (again, because by Lemma 51, $|f| \le 2\sigma < {{\,\textrm{dist}\,}}_p(u, \mathcal {C})$) it follows that $C_i(v) = C_i(u) \cup C_{i+1}(u)$. Thus, we obtain

$$\begin{aligned} z_i + z_{i+1}&= y_i - {{\,\textrm{sgn}\,}}(y_i) \cdot \!\sum _{\ell \in C_i(u)} d_\ell + y_{i+1} - {{\,\textrm{sgn}\,}}(y_{i+1}) \cdot \!\!\sum _{\ell \in C_{i+1}(u)} d_\ell \\&= y_i + y_{i+1} - {{\,\textrm{sgn}\,}}(y_i + y_{i+1}) \cdot \!\sum _{\ell \in C_i(v)} d_\ell . \end{aligned}$$

Second, we look at the case where $y_i$ and $y_{i+1}$ have opposite sign. We assume $|y_i| \ge |y_{i+1}|$. The other case is symmetric. We have $C_{i+1}(u) \subseteq C_i(u)$ and $C_i(v) = C_i(u) \setminus C_{i+1}(u)$. This implies

$$\begin{aligned} z_i + z_{i+1}&= y_i - {{\,\textrm{sgn}\,}}(y_i) \cdot \sum _{\ell \in C_i(u)} d_\ell + y_{i+1} - {{\,\textrm{sgn}\,}}(y_{i+1}) \cdot \sum _{\ell \in C_{i+1}(u)} d_\ell \\&= y_i + y_{i+1} - {{\,\textrm{sgn}\,}}(y_i) \cdot \left( \sum _{\ell \in C_i(u)} d_\ell - \sum _{\ell \in C_{i+1}(u)} d_\ell \right) \\&= y_i + y_{i+1} - {{\,\textrm{sgn}\,}}(y_i + y_{i+1}) \cdot \sum _{\ell \in C_i(v)} d_\ell .\end{aligned}$$

Note that in the case that $y_i = -y_{i+1}$ we have $C_i(u) = C_{i+1}(u)$ and $C_i(v)= \emptyset$, so the last equality also holds in this case. This concludes the proof of the lemma. $\square$

Lemma 61

If ${{\,\textrm{dist}\,}}_p(u, \mathcal {C}) > 5k\sigma \mu (u)$ and $u \overset{k}{\underset{R}{\Longrightarrow }} v$, then $\mathcal {S}_{\mathcal {C}}(u) \overset{k}{\underset{R}{\Longrightarrow }} \mathcal {S}_{\mathcal {C}}(v)$.

Proof

We prove the lemma by induction on k. If $k=1$, then the statement follows from Lemma 60. If $k>1$, then there is a $u' \in M(\Delta , I_\Delta )$ such that

$$\begin{aligned} u \underset{R}{\Longrightarrow }\ u' \overset{k-1}{\underset{R}{\Longrightarrow }} v. \end{aligned}$$

By Lemma 54 we have ${{\,\textrm{dist}\,}}_p(u', \mathcal {C}) > 5(k - 1)\sigma \mu (u)$. As none of the rules of $R$ increases $\mu (\cdot )$, it follows that ${{\,\textrm{dist}\,}}_p(u', \mathcal {C}) > 5(k - 1)\sigma \mu (u')$. Therefore, $\mathcal {S}_{\mathcal {C}}(u') \overset{k-1}{\underset{R}{\Longrightarrow }} \mathcal {S}_{\mathcal {C}}(v)$ by induction. By Lemma 60 we have $\mathcal {S}_{\mathcal {C}}(u) \underset{R}{\Longrightarrow }\ \mathcal {S}_{\mathcal {C}}(u')$. Combining those statements we conclude $\mathcal {S}_{\mathcal {C}}(u) \overset{k}{\underset{R}{\Longrightarrow }} \mathcal {S}_{\mathcal {C}}(v)$.

We continue by defining a concrete set of intervals $\mathcal {C}_{u,p}^K$ based on the following intuitive idea. From Lemma 50 and Corollary 53 we know that $\pi (u) =_G 1$ if and only if $u \overset{\le k}{\underset{R}{\Longrightarrow }} 1$ with $k = 10\sigma ^2|u|_\Delta ^2\mu (u)$. By Lemma 54, each application of a rule changes $\eta _p(\cdot )$ by at most $5\sigma \mu (u)$. Thus, the partial sums of the exponents change by less than

$$\begin{aligned} K = 50\sigma ^3|u|_\Delta ^2\mu (u)^2 + 1{.} \end{aligned}$$

Let $\left\{ c_1, \dots c_\ell \right\} = \left\{ \eta _p^i(u) \mid i \in [0, m] \right\}$ be the ordered set of the $\eta _p^i(u)$, i.e., $c_1< \dots < c_\ell$. We define the set of intervals

$$\begin{aligned} \mathcal {C}_{u,p}^K = \left\{ [c_i + K, c_{i+1} - K] \mid i \in [1, \ell -1], c_{i+1} - c_i \ge 2K \right\} . \end{aligned}$$

(9)

Let us write $\mathcal {C}$ for $\mathcal {C}_{u, p}^K$ in the following. Note that $\left| \mathcal {C}\right| \le m$. The next lemma shows that the shortened word computed with the set $\mathcal {C}$ is the identity if and only if the original word is the identity.

Lemma 62

$\pi (u) =_G 1$ if and only if $\pi (\mathcal {S}_{\mathcal {C}}(u)) =_G 1$.

Proof

Let $k = 10\sigma ^2|u|_\Delta ^2\mu (u)$. From the definition of $\mathcal {C}$ we obtain ${{\,\textrm{dist}\,}}_p(u, \mathcal {C}) > 5k\sigma \mu (u)$.

First, let $\pi (u) =_G 1$. By Lemma 50 (point 4) this is equivalent to $u \overset{*}{\underset{R}{\Longrightarrow }} 1$, which by Corollary 53 is equivalent to $u \overset{\le k}{\underset{R}{\Longrightarrow }} 1$. By Lemma 61 we have $\mathcal {S}_{\mathcal {C}}(u) \overset{*}{\underset{R}{\Longrightarrow }} \mathcal {S}_{\mathcal {C}}(1) = 1$. Applying Lemma 50 (point 2) we obtain $\pi (\mathcal {S}_{\mathcal {C}}(u)) \overset{*}{\underset{T}{\Longrightarrow }} 1$ and, hence, $\pi (\mathcal {S}_{\mathcal {C}}(u)) =_G 1$.

Second, assume that $\pi (u) \ne _G 1$. Since $R$ is terminating, there is some $v \in {{\,\textrm{IRR}\,}}(R)$ with $u \overset{*}{\underset{R}{\Longrightarrow }} {v}$. We cannot have $v = 1$ as this, by Lemma 50 (point 2), would yield $\pi (u) =_G 1$. Hence, we have $v \ne 1$. Moreover, Corollary 53 implies $u \overset{\le k}{\underset{R}{\Longrightarrow }} {v}$ and with Lemma 61 we get $\mathcal {S}_{\mathcal {C}}(u) \overset{*}{\underset{R}{\Longrightarrow }} \mathcal {S}_{\mathcal {C}}(v)$. By Lemma 57 we have $\mathcal {S}_{\mathcal {C}}(v) \in {{\,\textrm{IRR}\,}}(R)$. As the shortening process does not remove any letters but only replaces them, we have $\mathcal {S}_{\mathcal {C}}({v}) \ne _{M(\Delta ,I_\Delta )} 1$. It follows that $\pi (\mathcal {S}_{\mathcal {C}}({v})) \ne _G 1$ (otherwise, Lemma 50 (point 4) implies $\mathcal {S}_{\mathcal {C}}(v)\notin {{\,\textrm{IRR}\,}}(R)$). Finally, with 50 (point 2) we get $\pi (\mathcal {S}_{\mathcal {C}}(u)) =_G \pi (\mathcal {S}_{\mathcal {C}}({v})) \ne _G 1$. $\square$

The next lemma shows that when using the set $\mathcal {C}$ from (9), the exponents of the shortened word are bounded by a polynomial.

Lemma 63

Let $\mathcal {S}_{\mathcal {C}}(u) = u_0 (\beta _1,p^{z_1},\alpha _1) u_1 \cdots (\beta _m,p^{z_m},\alpha _m) u_m$ for some $u \in M(\Delta , I_\Delta )$. Then $|z_i| \le 101m\sigma ^3|u|_\Delta ^2\mu (u)^2$ for all $i \in [1, m]$.

Proof

We have

$$\begin{aligned} |z_i|&= \Bigl |y_i - {{\,\textrm{sgn}\,}}(y_i)\cdot \sum _{j \in C_i} d_j \Bigr |\\&= \left|y_i \right|- \sum _{j \in C_i} d_j \\&\overset{\text {(A)}}{=} \left|y_i \right|- \sum _{j \in C_i} \max \{0, c_{j+1} - c_{j} - 2K + 1\} \\&\le \left|y_i \right|- \sum _{j \in C_i} (c_{j+1} - c_{j} - 2K + 1)\\&= \left|y_i \right|- \sum _{j \in C_i} (c_{j+1} - c_{j}) + \sum _{j \in C_i} (2K - 1)\\&= \sum _{j \in C_i} (2K - 1) \\&\overset{\text {(B)}}{\le } m(2K - 1) \le 2mK, \end{aligned}$$

where we used the following facts:

(A):

Definition of $\mathcal {C}$ in (9).

(B):

$|C_i| \le |\mathcal {C}| \le m$.

The lemma follows by plugging in $K = 50\sigma ^3|u|_\Delta ^2\mu (u)^2 + 1$. $\square$

5.3.4 Solving the power word problem

Now we are ready for the proofs of our main results for graph products.

Theorem 64

Let $G = {{\,\textrm{GP}\,}}(\mathcal {L}, I, \left( G_\zeta \right) _{\zeta \in \mathcal {L}})$ be a graph product of f.g. groups such that no $G_\zeta$ contains any element a with $a^2=_{G_\zeta } 1$ and $a\ne _{G_\zeta } 1$. Then the power word problem in G can be decided in $\textsf{uAC} ^0$ with oracle gates for the word problem in $F_2$ and for the power word problems in the base groups $G_\zeta$.

Proof

By Lemma 45 the preprocessing can be done in $\textsf{uAC} ^0$ with oracles for the word problems in G and $F_2$ (thus, by [33, Theorem 5.6.5, Theorem 5.6.14] in $\textsf{uAC} ^0(\text {WP}(F_2), (\text {WP}(G_\zeta ))_{\zeta \in \mathcal {L}}) \subseteq \textsf{uAC} ^0(\text {WP}(F_2), ({{\,\textrm{PowWP}\,}}(G_\zeta ))_{\zeta \in \mathcal {L}})$). Let (6) be the power word obtained after the preprocessing. The shortening procedure can be computed in parallel for each $p \in \{p_i \mid i \in [1, n]\}$. It requires iterated additions, which is in $\textsf{uTC} ^0 \subseteq \textsf{uAC} ^0(\text {WP}(F_2))$. By Lemma 63 the exponents of the shortened word are bounded by a polynomial in the input length. We write the shortened word as a simple power word of polynomial length and solve the simple power word problem, which by Lemma 18, is in $\textsf{uAC} ^0(\text {WP}(F_2), ({{\,\textrm{PowWP}\,}}(G_\zeta ))_{\zeta \in \mathcal {L}})$. $\square$

Corollary 65

Let G be a RAAG. The power word problem in G is $\textsf{uAC} ^0$-Turing reducible to the word problem in the free group $F_2$ and, thus, in $\textsf{L}$.

The proof of the following result is analogous to the proof of Theorem 64 using the respective statements of the lemmas for the uniform case.

Theorem 66

Let $\mathcal {C}$ be a non-trivial class of f.g. groups such that for all $G \in \mathcal {C}$ and all $a \in G \setminus \{1\}$ we have $a^2\ne _{G} 1$. Then ${{\,\textrm{UPowWP}\,}}({{\,\textrm{GP}\,}}(\mathcal {C}))$ belongs to $\textsf{uAC} ^0\big [\textsf{C}_=\textsf{L} ^{{{\,\textrm{UPowWP}\,}}(\mathcal {C})}\big ]$.

Corollary 67

Let $\textrm{RAAG}$ denote the class of finitely generated RAAGs given by an alphabet X and an independence relation $I \subseteq X \times X$. Then ${{\,\textrm{UPowWP}\,}}(\textrm{RAAG})$ is in $\textsf{uAC} ^0\big [\textsf{C}_=\textsf{L} \big ] \subseteq \textsf{uNC} ^{2}$.

Remark 68

One can consider variants of the power word problem, where the exponents are not given in binary representation but in even more compact forms. Power circuits as defined in [53] are such a representation that allow non-elementary compression for some integers. Our logspace algorithm for the power word problem in a RAAG involves iterated addition and comparison (for equality) of exponents. For arbitrary power circuits, unfortunately, comparison for less than is P-complete and the complexity for equality checking is unknown. However, if we restrict to certain normal forms, called reduced power circuits, both iterated addition and comparison (for equality and for less than) are in $\textsf{uTC}^0$ [48]. Therefore, our techniques show that the power word problem for RAAGs with exponents given by reduced power circuits is also $\textsf{uAC}^0$-Turing-reducible to the word problem for the free group $F_2$.

6 Consequences for the Knapsack Problem in Right-angled Artin Groups

Recall that the knapsack problem for a finitely generated group G asks, whether for given group elements $g_1, \ldots , g_n,g \in G$ (represented by words over generators) there exist $x_1, \ldots , x_n \in \mathbb {N}$ such that $g_1^{x_1} \cdots g_n^{x_n} =_G g$ holds. Using our results on the power word problem, we can show the following result, which solves an open problem from [44].

Corollary 69

The uniform knapsack problem for RAAGs is $\textsf{NP}$-complete: On input of a RAAG $G = G(X,I)$, given by the graph (X, I), and $u_1, \dots , u_n, u \in (X \cup \overline{X})^*$, it can be decided in $\textsf{NP}$ whether there are $x_1, \dots , x_n \in \mathbb {N}$ with $u_1^{x_1} \cdots u_n^{x_n} =_G u$.

Proof

Let $N = |X| + |u| + \sum _{i=1}^n |u_i|$ (this is roughly the input size). By [44, Theorem 3.11], there is a polynomial p(N) such that if there is a solution, then there is a solution $x_1, \dots , x_n$ with $x_i \le 2^{p(N)}$. Therefore, we can guess a potential solution in polynomial time. From Corollary 67 it follows that the uniform power word problem in RAAGs belongs to $\textsf {P}$. Hence, the uniform knapsack problem can be decided in $\textsf{NP}$. Finally, $\textsf{NP}$-completeness follows immediately from the $\textsf{NP}$-completeness of the knapsack problem for a certain fixed RAAG, which has been shown in [44]. $\square$

Note that this proof even shows $\textsf{NP}$-completeness of the slightly more general problem of uniformly solving exponent equations for RAAGs as defined in [44].

7 Open Problems

We strongly conjecture that the requirement $a^2 \ne 1$ can be dropped in all our results (as falsely claimed in [58, 59]). Indeed, we believe that our methods can be extended to cope with that case. Still, this is a highly non-trivial question for further research.

Furthermore, we conjecture that the method of Section 5.3 can similarly be applied to hyperbolic groups, and hence that the power word problem for a hyperbolic group G is $\textsf{uAC}^{0}$-Turing-reducible to the word problem for G. One may also try to prove transfer results for the power word problem with respect to group theoretical constructions other than graph products, e.g., HNN extensions and amalgamated products over finite subgroups. For a transfer result with respect to wreath products, see [19, Proposition 19]. However, many cases are still open.

For finitely generated linear groups, the power word problem leads to the problem of computing matrix powers with binary encoded exponents. The complexity of this problem is open; variants of this problem have been studied in [3, 21].

Another open question is what happens if we allow nested exponents. We conjecture that in the free group for any nesting depth bounded by a constant the problem is still in $\textsf{uAC}^0 (\text {WP}(F_2))$. However, for unbounded nesting depth it is not clear what happens: we only know that it is in P since it is a special case of the compressed word problem; but it still could be in $\textsf{uAC}^0 (\text {WP}(F_2))$ or it could be P-complete or somewhere in between.