Skip to main content
SpringerLink
Log in

Monodromy and vanishing cycles in toric surfaces

  • Published:
Inventiones mathematicae Aims and scope

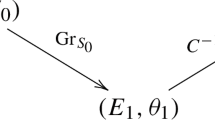
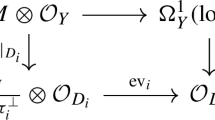Abstract

Given an ample line bundle on a toric surface, a question of Donaldson asks which simple closed curves can be vanishing cycles for nodal degenerations of smooth curves in the complete linear system. This paper provides a complete answer. This is accomplished by reformulating the problem in terms of the mapping class group-valued monodromy of the linear system, and giving a precise determination of this monodromy group.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Chillingworth, D.: Winding numbers on surfaces. I. Math. Ann. 196, 218–249 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  2. Chillingworth, D.: Winding numbers on surfaces. II. Math. Ann. 199, 131–153 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  3. Crétois, R., Lang, L.: The Vanishing Cycles of Curves in Toric Surfaces I. Preprint. arXiv:1701.00608v2.pdf (2017)

  4. Crétois, R., Lang, L.: The Vanishing Cycles of Curves in Toric Surfaces II. Preprint. arXiv:1706.07252.pdf (2017)

  5. Dieudonné, J.: Sur les groupes classiques. Hermann, Paris (1973). Troisième édition revue et corrigée, Publications de l’Institut de Mathématique de l’Université de Strasbourg, VI, Actualités Scientifiques et Industrielles, No. 1040

  6. Donaldson, S.: Polynomials, vanishing cycles and Floer homology. In: Mathematics: Frontiers and Perspectives, pp. 55–64. American Mathematical Society, Providence (2000)

  7. Farb, B., Margalit, D.: A Primer on Mapping Class Groups, Volume 49 of Princeton Mathematical Series. Princeton University Press, Princeton, NJ (2012)

  8. Grove, L.C.: Classical Groups and Geometric Algebra, Volume 39 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI (2002)

  9. Humphries, S., Johnson, D.: A generalization of winding number functions on surfaces. Proc. Lond. Math. Soc. (3) 58(2), 366–386 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  10. Johnson, D.: An abelian quotient of the mapping class group \({\cal{I}}_{g}\). Math. Ann. 249(3), 225–242 (1980)

    Article  MathSciNet  Google Scholar 

  11. Johnson, D.: Spin structures and quadratic forms on surfaces. J. Lond. Math. Soc. (2) 22(2), 365–373 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  12. Johnson, D.: A survey of the Torelli group. In: Low-Dimensional Topology (San Francisco, Calif., 1981), Volume 20 of Contemporary Mathematics, pp. 165–179. American Mathematical Society, Providence (1983)

  13. Johnson, D.: The structure of the Torelli group. II. A characterization of the group generated by twists on bounding curves. Topology 24(2), 113–126 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  14. Johnson, D.: The structure of the Torelli group. III. The abelianization of \(\mathscr {T}\). Topology 24(2), 127–144 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  15. Matsumoto, M.: A presentation of mapping class groups in terms of Artin groups and geometric monodromy of singularities. Math. Ann. 316(3), 401–418 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  16. Putman, A.: A note on the connectivity of certain complexes associated to surfaces. Enseign. Math. (2) 54(3–4), 287–301 (2008)

    MathSciNet  MATH  Google Scholar 

  17. Salter, N.: On the Monodromy Group of the Family of Smooth Plane Curves. Preprint. arXiv:1610.04920.pdf (2016)

Download references

Acknowledgements

The author would like to extend his warmest thanks to R. Crétois and L. Lang for helpful discussions of their work. He would also like to acknowledge C. McMullen for some insightful comments on a preliminary draft, and M. Nichols for a productive conversation. A special thanks is due to an anonymous referee for a very careful reading of the preprint and for many useful suggestions, both mathematical and expository.

Author information

Authors and Affiliations

  1. Department of Mathematics, Columbia University, 2990 Broadway, New York, NY, 10027, USA

    Nick Salter

Authors
  1. Nick Salter
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nick Salter.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This material is based upon work supported by the National Science Foundation under Award No. DMS-1703181.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Salter, N. Monodromy and vanishing cycles in toric surfaces. Invent. math. 216, 153–213 (2019). https://doi.org/10.1007/s00222-018-0845-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00222-018-0845-6

Search

Navigation