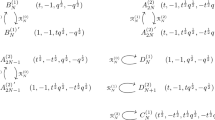Unitary Representations of Uq(??}(2,ℝ)),¶the Modular Double and the Multiparticle q-Deformed¶Toda Chain

Abstract:

The paper deals with the analytic theory of the quantum q-deformed Toda chains; the technique used combines the methods of representation theory and the Quantum Inverse Scattering Method. The key phenomenon which is under scrutiny is the role of the modular duality concept (first discovered by L. Faddeev) in the representation theory of noncompact semisimple quantum groups. Explicit formulae for the Whittaker vectors are presented in terms of the double sine functions and the wave functions of the N-particle q-deformed open Toda chain are given as a multiple integral of the Mellin–Barnes type. For the periodic chain the two dual Baxter equations are derived.