A Proof of Friedman’s Ergosphere Instability for Scalar Waves

Abstract

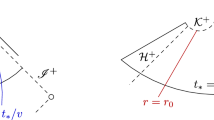
Let ${(\mathcal{M}^{3+1},g)}$ be a real analytic, stationary and asymptotically flat spacetime with a non-empty ergoregion ${\mathscr{E}}$ and no future event horizon ${\mathcal{H}^{+}}$. In Friedman (Commun Math Phys 63(3):243–255, 1978), Friedman observed that, on such spacetimes, there exist solutions ${\varphi}$ to the wave equation ${\square_{g}\varphi=0}$ such that their local energy does not decay to 0 as time increases. In addition, Friedman provided a heuristic argument that the energy of such solutions actually grows to ${+\infty}$. In this paper, we provide a rigorous proof of Friedman’s instability. Our setting is, in fact, more general. We consider smooth spacetimes ${(\mathcal{M}^{d+1},g)}$, for any ${d\ge2}$, not necessarily globally real analytic. We impose only a unique continuation condition for the wave equation across the boundary ${\partial\mathscr{E}}$ of ${\mathscr{E}}$ on a small neighborhood of a point ${p\in\partial\mathscr{E}}$. This condition always holds if ${(\mathcal{M},g)}$ is analytic in that neighborhood of p, but it can also be inferred in the case when ${(\mathcal{M},g)}$ possesses a second Killing field ${\Phi}$ such that the span of ${\Phi}$ and the stationary Killing field T is timelike on ${\partial\mathscr{E}}$. We also allow the spacetimes ${(\mathcal{M},g)}$ under consideration to possess a (possibly empty) future event horizon ${\mathcal{H}^{+}}$, such that, however, ${\mathcal{H}^{+}\cap\,\,\mathscr{E}=\emptyset}$ (excluding, thus, the Kerr exterior family). As an application of our theorem, we infer an instability result for the acoustical wave equation on the hydrodynamic vortex, a phenomenon first investigated numerically by Oliveira et al. in (Phys Rev D 89(12):124008, 2014). Furthermore, as a side benefit of our proof, we provide a derivation, based entirely on the vector field method, of a Carleman-type estimate on the exterior of the ergoregion for a general class of stationary and asymptotically flat spacetimes. Applications of this estimate include a Morawetz-type bound for solutions ${\varphi}$ of ${\square_{g}\varphi=0}$ with frequency support bounded away from ${{\omega}=0}$ and ${{\omega}=\pm\infty}$.