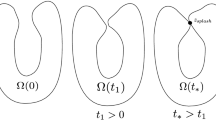Skip to main content
SpringerLink
Log in

On the Finite-Time Splash and Splat Singularities for the 3-D Free-Surface Euler Equations

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

We prove that the 3-D free-surface incompressible Euler equations with regular initial geometries and velocity fields have solutions which can form a finite-time “splash” (or “splat”) singularity first introduced in Castro et al. (Splash singularity for water waves, http://arxiv.org/abs/1106.2120v2, 2011), wherein the evolving 2-D hypersurface, the moving boundary of the fluid domain, self-intersects at a point (or on surface). Such singularities can occur when the crest of a breaking wave falls unto its trough, or in the study of drop impact upon liquid surfaces. Our approach is founded upon the Lagrangian description of the free-boundary problem, combined with a novel approximation scheme of a finite collection of local coordinate charts; as such we are able to analyze a rather general set of geometries for the evolving 2-D free-surface of the fluid. We do not assume the fluid is irrotational, and as such, our method can be used for a number of other fluid interface problems, including compressible flows, plasmas, as well as the inclusion of surface tension effects.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Adams R.A.: Sobolev Spaces. Academic Press, London-New York (1978)

    Google Scholar 

  2. Alazard, T., Burq, N., Zuily, C.: On the Cauchy problem for gravity water waves. http://arxiv.org/abs/1212.0626v1 [math.AP], 2012

  3. Alvarez-Samaniego B., Lannes D.: Large time existence for 3D water-waves and asymptotics. Invent. Math. 171, 485–541 (2008)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  4. Ambrose D.M., Masmoudi N.: The zero surface tension limit of two-dimensional water waves. Commun. Pure Appl. Math. 58, 1287–1315 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  5. Ambrose D., Masmoudi N.: The zero surface tension limit of three-dimensional water waves. Indiana Univ. Math. J. 58, 479–521 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  6. Beale J.T., Hou T., Lowengrub J.: Growth rates for the linearized motion of fluid interfaces away from equilibrium. Commun. Pure Appl. Math. 46, 1269–1301 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  7. Castro A., Córdoba D., Fefferman C., Gancedo F., López-Fernández M.: Rayleigh–Taylor breakdown for the Muskat problem with applications to water waves. Ann. Math. 175, 909–948 (2012)

    Article  MATH  Google Scholar 

  8. Castro A., Córdoba D., Fefferman C., Gancedo F., López-Fernández M.: Turning waves and breakdown for incompressible flows. Proc. Natl. Acad. Sci. 108, 4754–4759 (2011)

    Article  ADS  MATH  Google Scholar 

  9. Castro, A., Córdoba, D., Fefferman, C., Gancedo, F., Gómez-Serrano, M.: Splash singularity for water waves. http://arxiv.org/abs/1106.2120v2 [math.AP], 2011

  10. Castro, A., Córdoba, D., Fefferman, C., Gancedo, F., Gómez-Serrano, M.: Finite time singularities for the free boundary incompressible Euler equations. Ann. Math. (2013) (to appear). http://arxiv.org/abs/1112.2170v3 [math.AP]

  11. Craig W.: An existence theory for water waves and the Boussinesq and Korteweg-de Vries scaling limits. Commun. Part. Differ. Eqs. 10(8), 787–1003 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  12. Christodoulou D., Lindblad H.: On the motion of the free surface of a liquid. Commun. Pure Appl. Math. 53, 1536–1602 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  13. Cheng A., Coutand D., Shkoller S.: On the motion of vortex sheets with surface tension in the 3D euler equations with vorticity. Commun. Pure Appl. Math. 61, 1715–1752 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  14. Coutand D., Shkoller S.: Well-posedness of the free-surface incompressible Euler equations with or without surface tension. J. Am. Math. Soc. 20, 829–930 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  15. Coutand D., Shkoller S.: A simple proof of well-posedness for the free-surface incompressible Euler equations. Disc. Cont. Dyn. Syst. Ser. S 3, 429–449 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  16. Coutand D., Shkoller S.: Well-posedness in smooth function spaces for the moving-boundary 3-D compressible Euler equations in physical vacuum. Arch. Rational Mech. Anal. 206, 515–616 (2012)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  17. Ebin D.: The equations of motion of a perfect fluid with free boundary are not well posed. Comm. Partial Differ. Equ. 10, 1175–1201 (1987)

    Article  MathSciNet  Google Scholar 

  18. Germain P., Masmoudi N., Shatah J.: Global solutions for the gravity water waves equation in dimension 3. C. R. Math. Acad. Sci. Paris 347, 897–902 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  19. Howison S.D., Ockendon J.R., Oliver J.M., Purvis R., Smith F.T.: Droplet impact on a thin fluid layer. J. Fluid Mech. 542, 1–23 (2005)

    Article  ADS  MathSciNet  Google Scholar 

  20. Lannes D.: Well-posedness of the water-waves equations. J. Am. Math. Soc. 18, 605–654 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  21. Lindblad H.: Well-posedness for the motion of an incompressible liquid with free surface boundary. Ann. Math. 162, 109–194 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  22. Nalimov V.I.: The Cauchy–Poisson problem (in Russian), Dynamika Splosh. Sredy 18, 104–210 (1974)

    MathSciNet  Google Scholar 

  23. Og̃uz N.H., Prosperetti A.: Bubble entrainment by the impact of drops on liquid surfaces. J. Fluid Mech. 219, 143–179 (1990)

    Article  ADS  MathSciNet  Google Scholar 

  24. Rayleigh L.: On the instability of jets. Proc. Lond. Math. Soc. s1-10(1), 4–13 (1878)

    Article  Google Scholar 

  25. Temam, R.: Navier–Stokes equations. Theory and numerical analysis. 3rd edn. In: Studies in Mathematics and its Applications, Vol. 2. Amsterdam: North-Holland Publishing Co., 1984

  26. Shatah J., Zeng C.: Geometry and a priori estimates for free boundary problems of the Euler equation. Commun. Pure Appl. Math. 61, 698–744 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  27. Taylor G.: The instability of liquid surfaces when accelerated in a direction perpendicular to their planes I. Proc. R. Soc. Lond. Ser. A. 201, 192–196 (1950)

    Article  ADS  MATH  Google Scholar 

  28. Worthington, M.: The splash of a drop and allied phenomena. Washington, DC: US Govt.Printing Office, Smithsonian Report, 1894. (Reprinted with additions: A Study of Splashes. London: Macmillan, 1963)

  29. Wu S.: Well-posedness in Sobolev spaces of the full water wave problem in 2-D. Invent. Math. 130, 39–72 (1997)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  30. Wu S.: Well-posedness in Sobolev spaces of the full water wave problem in 3-D. J. Am. Math. Soc. 12, 445–495 (1999)

    Article  MATH  Google Scholar 

  31. Wu S.: Almost global wellposedness of the 2-D full water wave problem. Invent. Math. 177, 45–135 (2009)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  32. Wu S.: Global wellposedness of the 3-D full water wave problem. Invent. Math. 184, 125–220 (2011)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  33. Yosihara H.: Gravity waves on the free surface of an incompressible perfect fluid. Publ. RIMS Kyoto Univ. 18, 49–96 (1982)

    Article  MATH  MathSciNet  Google Scholar 

  34. Zhang P., Zhang Z.: On the free boundary problem of three-dimensional incompressible Euler equations. Commun. Pure Appl. Math. 61, 877–940 (2008)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematical and Computer Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, UK

    Daniel Coutand

  2. Department of Mathematics, University of California, Davis, CA, 95616, USA

    Steve Shkoller

Authors
  1. Daniel Coutand
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Steve Shkoller
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Steve Shkoller.

Additional information

Communicated by P. Constantin

Rights and permissions

Reprints and permissions

About this article

Cite this article

Coutand, D., Shkoller, S. On the Finite-Time Splash and Splat Singularities for the 3-D Free-Surface Euler Equations. Commun. Math. Phys. 325, 143–183 (2014). https://doi.org/10.1007/s00220-013-1855-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-013-1855-2

Keywords

Search

Navigation