Skip to main content
SpringerLink
Log in

The Periodic Oscillation of an Adiabatic Piston in Two or Three Dimensions

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

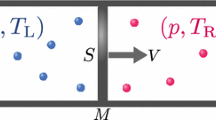
We study a heavy piston of mass M that separates finitely many ideal, unit mass gas particles moving in two or three dimensions. Neishtadt and Sinai previously determined a method for finding this system’s averaged equation and showed that its solutions oscillate periodically. Using averaging techniques, we prove that the actual motions of the piston converge in probability to the predicted averaged behavior on the time scale M 1/2 when M tends to infinity while the total energy of the system is bounded and the number of gas particles is fixed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Anosov D.V. (1960). Averaging in systems of ordinary differential equations with rapidly oscillating solutions. Izv. Akad. Nauk SSSR Ser. Mat. 24: 721–742

    MATH  Google Scholar 

  2. Bálint P., Chernov N., Szász D. and Tóth I.P. (2003). Geometry of multi-dimensional dispersing billiards. Astérisque 286(xviii): 119–150

    Google Scholar 

  3. Bunimovich L.A. and Rehacek J. (1998). On the ergodicity of many-dimensional focusing billiards. Ann. Inst. H. Poincaré Phys. Théor. 68(4): 421–448

    MATH  Google Scholar 

  4. Bunimovich L.A. (1979). On the ergodic properties of nowhere dispersing billiards. Commun. Math. Phys. 65(3): 295–312

    Article  MATH  ADS  Google Scholar 

  5. Callen H.B. (1963). Thermodynamics. Wiley, New York

    Google Scholar 

  6. Chernov, N., Dolgopyat, D.: Brownian brownian motion - I. Memoirs of the American Mathematical Society, to appear, 2006

  7. Chernov, N., Dolgopyat, D.: Hyperbolic billiards and statistical physics. In: Proceedings of the International Congress of Mathematicians, (Madrid, Spain, 2006), Vol. II, Berlin: European Math. Soc., 2007, pp. 1679–1704

  8. Crosignani B., Di Porto P. and Segev M. (1996). Approach to thermal equilibrium in a system with adiabatic constraints. Am. J. Phys. 64(5): 610–613

    Article  ADS  Google Scholar 

  9. Chernov N. (1997). Entropy, Lyapunov exponents and mean free path for billiards. J. Stat. Phys. 88(1-2): 1–29

    Article  MATH  Google Scholar 

  10. Chernov, N.: On a slow drift of a massive piston in an ideal gas that remains at mechanical equilibrium. Math. Phys. Electron. J. 10, Paper 2, 18 pp. (electronic), (2004)

  11. Chernov N. and Lebowitz J.L. (2002). Dynamics of a massive piston in an ideal gas: oscillatory motion and approach to equilibrium. J. Stat. Phys. 109(3–4): 507–527

    Article  MATH  Google Scholar 

  12. Chernov N., Lebowitz J.L. and Sinai Ya. (2002). Scaling dynamics of a massive piston in a cube filled with ideal gas: exact results. J. Stat. Phys. 109(3–4): 529–548

    Article  MATH  Google Scholar 

  13. Chernov, N., Markarian, R.: Chaotic Billiards. Number 127 in Mathematical Surveys and Monographs. Providence, RI: Amer. Math. Soc. 2006

  14. Chernov N. and Markarian R. (2006). Dispersing billiards with cusps: slow decay of correlations. Commun. Math. Phys. 270(3): 727–758

    Article  ADS  Google Scholar 

  15. Dolgopyat, D.: Introduction to averaging. Available online at http://www.math.umd.edu/~dmitry/IANotes.pdf, 2005

  16. Gorelyshev, I.V., Neishtadt, A.I.: On the adiabatic perturbation theory for systems with impacts. Prikl. Mat. Mekh. 70(1), 6–19 (2006); English trans. in J. Appl. Math. and Mech. 70, 4–17 (2006)

  17. Gruber Ch., Pache S. and Lesne A. (2003). Two-time-scale relaxation towards thermal equilibrium of the enigmatic piston. J. Stat. Phys. 112(5–6): 1177–1206

    Article  MATH  Google Scholar 

  18. Gruber Ch. (1999). Thermodynamics of systems with internal adiabatic constraints: time evolution of the adiabatic piston. Eur. J. Phys. 20: 259–266

    Article  MATH  Google Scholar 

  19. Lochak P. and Meunier C. (1988). Multiphase Averaging for Classical Systems. Springer-Verlag, New York

    MATH  Google Scholar 

  20. Lebowitz, J., Sinai, Ya.G., Chernov, N.: Dynamics of a massive piston immersed in an ideal gas. Usp. Mat. Nauk., 57(6(348)), 3–86 (2002); English trans. in Russ. Math. Surv. 57(6) 1045–1125 (2002)

  21. Neishtadt A.I. and Sinai Ya.G. (2004). Adiabatic piston as a dynamical system. J. Stat. Phys. 116(1–4): 815–820

    Article  Google Scholar 

  22. Petersen K. (1983). Ergodic Theory. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  23. Santaló L.A. (1976). Integral Geometry and Geometric Probability. Addison Wesley, Reading, MA

    MATH  Google Scholar 

  24. Sinai, Ya.G.: Dynamics of a massive particle surrounded by a finite number of light particles. Teoret. Mat. Fiz. 121(1), 110–116 (1999); English trans. in Theoret. and Math. Phys. 121(1) 1351–1357 (1999)

  25. Sanders J.A. and Verhulst F. (1985). Averaging Methods in Nonlinear Dynamical Systems. Springer-Verlag, New York

    MATH  Google Scholar 

  26. Vorobets Ya.B. (1997). Ergodicity of billiards in polygons. Mat. Sb. 188(3): 65–112

    Google Scholar 

  27. Wright P. (2006). A simple piston problem in one dimension. Nonlinearity 19: 2365–2389

    Article  MATH  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Courant Institute of Mathematical Sciences, New York University, 251 Mercer St., New York, NY, 10012, USA

    Paul Wright

Authors
  1. Paul Wright
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Paul Wright.

Additional information

Communicated by G. Gallavotti

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wright, P. The Periodic Oscillation of an Adiabatic Piston in Two or Three Dimensions. Commun. Math. Phys. 275, 553–580 (2007). https://doi.org/10.1007/s00220-007-0317-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-007-0317-0

Keywords

Search

Navigation