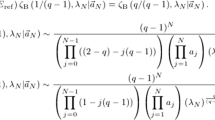Skip to main content
SpringerLink
Log in

Towards a Derivation of Fourier’s Law for Coupled Anharmonic Oscillators

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

We consider a Hamiltonian system made of weakly coupled anharmonic oscillators arranged on a three dimensional lattice \({\mathbb{Z}}_{2N} \times \mathbb{Z}^2\), and subjected to stochastic forcing mimicking heat baths of temperatures T 1 and T 2 on the hyperplanes at 0 and N. We introduce a truncation of the Hopf equations describing the stationary state of the system which leads to a nonlinear equation for the two-point stationary correlation functions. We prove that these equations have a unique solution which, for N large, is approximately a local equilibrium state satisfying Fourier law that relates the heat current to a local temperature gradient. The temperature exhibits a nonlinear profile.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. Aoki K., Kusnezov D. (2002). Nonequilibrium statistical mechanics of classical lattice φ 4 field theory. Ann. Phys. 295: 50–80

    Article  MATH  ADS  MathSciNet  Google Scholar 

  2. Aoki K., Lukkarinen J., Spohn H. (2006). Energy Transport in Weakly Anharmonic Chains. J. Stat. Phys. 124: 1105–1129

    Article  MATH  MathSciNet  ADS  Google Scholar 

  3. Bernardin C., Olla S. (2005). Fourier’s law for a microscopic model of heat conduction. J. Stat. Phys. 121: 271–289

    Article  MATH  MathSciNet  ADS  Google Scholar 

  4. Basile G., Bernardin C., Olla S. (2006). A momentum conserving model with anomalous thermal conductivity in low dimension. Phys. Rev. Lett. 96: 204303

    Article  ADS  Google Scholar 

  5. Basile, G., Bernardin, C., Olla, S.: Thermal conductivity for a momentum conserving model. http://arxiv.org/abs/cond-mat/0601544, 2006

  6. Bonetto, F., Lebowitz, J.L., Rey-Bellet, L.: Fourier Law: A challenge to Theorists. In: Mathematical Physics 2000, London: Imp. Coll. Press, 2000, pp. 128–150

  7. Bonetto F., Lebowitz J.L., Lukkarinen J. (2004). Fourier’s Law for a Harmonic Crystal with Self-consistent Stochastic Reservoirs. J. Stat. Phys. 116: 783–813

    Article  MATH  MathSciNet  ADS  Google Scholar 

  8. Cercignani C., Kremer G.M. (1999). On relativistic collisional invariants. J. Stat. Phys. 96: 439–445

    Article  MATH  MathSciNet  Google Scholar 

  9. Eckmann J.-P., Pillet C.-A., Rey-Bellet L. (1999). Non-equilibrium statistical mechanics of anharmonic chains coupled to two heat baths at different temperatures. Commun. Math. Phys. 201: 657–697

    Article  MATH  ADS  MathSciNet  Google Scholar 

  10. Eckmann J.-P., Pillet C.-A., Rey-Bellet L. (1999). Entropy production in non-linear, thermally driven Hamiltonian systems. J. Stat. Phys. 95: 305–331

    Article  MATH  MathSciNet  Google Scholar 

  11. Eckmann J.-P., Hairer M. (2000). Non-equilibrium statistical mechanics of strongly anharmonic chains of oscillators. Commun. Math. Phys. 212: 105–164

    Article  MATH  ADS  MathSciNet  Google Scholar 

  12. Eckmann J.-P., Hairer M. (2003). Spectral properties of hypoelliptic operators. Commun. Math. Phys. 235: 233–253

    Article  MATH  ADS  MathSciNet  Google Scholar 

  13. Eckmann, J.-P.: Non-equilibrium steady states. In: Proceedings of the International Congress of Mathematicians, Beijing, Vol. III, Beijing: Higher Education Press, 2002, pp. 409–418

  14. Eckmann J.-P., Young L.-S. (2004). Temperature profiles in Hamiltonian heat conduction. Europhys. Lett. 68: 790–796

    Article  ADS  MATH  MathSciNet  Google Scholar 

  15. Eckmann, J.-P., Young, L.-S.: Nonequilibrium energy profiles for a class of 1-D models. To appear in Commun. Math Phys

  16. Esposito, R., Pulvirenti, M.: From particles to fluids. In: Friedlander S., Serre D. (eds) Handbook of Mathematical Fluid Dynamics, Vol. III, Amsterdam: Elsevier Science, 2004

  17. Galves A., Kipnis C., Marchioro C., Presutti E. (1981). Nonequilibrium measures which exhibit a temperature gradient; study of a model. Commun. Math. Phys. 81: 127–147

    Article  MATH  ADS  MathSciNet  Google Scholar 

  18. Golse F., Sant-Raymond L. (2004). The Navier-Stokes limit of the Boltzmann equation for bounded collision kernels. Invent. Math. 155: 81–161

    Article  MATH  MathSciNet  Google Scholar 

  19. Hérau, F., Nier, F.: Isotropic hypoellipticity and trend to equilibrium for the Fokker-Planck equation with high degree potential. Arch. Rat. Mech. Anal. 171, 151, 218 (2004)

    Google Scholar 

  20. Kipnis C., Marchioro C., Presutti E. (1982). Heat flow in an exactly solvable model. J. Stat. Phys. 27: 65–74

    Article  MathSciNet  ADS  Google Scholar 

  21. Lefevere, R., Schenkel, A.: Normal heat conductivity in a strongly pinned chain of anharmonic oscillators. J. Stat. Mech., L02001 (2006), available on: http://www.iop.org/EJ/toc/1742-5468/2006/02, 2006

  22. Lepri S., Livi R., Politi A. (2003). Thermal conductivity in classical low-dimensional lattices. Phys. Reports 377: 1–80

    Article  ADS  MathSciNet  Google Scholar 

  23. Lepri S., Livi R., Politi A. (1998). On the anomalous thermal conductivity of one-dimensional lattices. Europhys. Lett. 43: 271

    Article  ADS  Google Scholar 

  24. Narayan O., Ramaswamy S. (2002). Anomalous heat conduction in one-dimensional momentum-conserving systems. Phys. Rev. Lett. 89: 200601

    Article  ADS  Google Scholar 

  25. Pereverzev A. (2003). Fermi-Pasta-Ulam β lattice: Peierls equation and anomalous heat conductivity. Phys. Rev. E. 68: 056124

    Article  ADS  MathSciNet  Google Scholar 

  26. Rey-Bellet L., Thomas L.E. (2000). Asymptotic behavior of thermal non-equilibrium steady states for a driven chain of anharmonic oscillators. Commun. Math. Phys. 215: 1–24

    Article  MATH  ADS  MathSciNet  Google Scholar 

  27. Rey-Bellet L., Thomas L.E. (2002). Exponential convergence to non-equilibrium stationary states in classical statistical mechanics. Commun. Math. Phys. 225: 305–329

    Article  MATH  ADS  MathSciNet  Google Scholar 

  28. Rey-Bellet, L.: Nonequilibrium statistical mechanics of open classical systems. In: XIVTH International Congress on Mathematical Physics, edited by Jean-Claude Zambrini, Singapore: World Scientific, 2006

  29. Rieder Z., Lebowitz J.L., Lieb E. (1967). Properties of a harmonic crystal in a stationary non-equilibrium state. J. Math. Phys. 8: 1073–1085

    Article  ADS  Google Scholar 

  30. Spohn H., Lebowitz J.L. (1977). Stationary non-equilibrium states of infinite harmonic systems. Commun. Math. Phys. 54: 97–120

    Article  ADS  MathSciNet  Google Scholar 

  31. Spohn H. (2006). The phonon Boltzmann equation, properties and link to weakly anharmonic lattice dynamics. J. Stat. Phys. 124: 1041–1104

    Article  MATH  MathSciNet  ADS  Google Scholar 

  32. Spohn H. (2006). Collisional invariants for the phonon Boltzmann equation. J. Stat. Phys. 124: 1131–1135

    Article  MATH  MathSciNet  ADS  Google Scholar 

  33. Titchmarsh, E.C.: Introduction to the Theory of Fourier Integrals. Oxford: Clarendon Press, 1948

  34. Villani, C.: A review of mathematical topics in collisional kinetic theory. In: Friedlander, S., Serre, D., (eds.) Handbook of Mathematical Fluid Dynamics, Vol. I. Amsterdam: Elsevier Science, 2002

Download references

Author information

Authors and Affiliations

  1. UCL, FYMA, chemin du Cyclotron 2, B-1348, Louvain-la-Neuve, Belgium

    Jean Bricmont

  2. Department of Mathematics, Helsinki University, P.O. Box 4, 00014, Helsinki, Finland

    Antti Kupiainen

Authors
  1. Jean Bricmont
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Antti Kupiainen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Antti Kupiainen.

Additional information

Communicated by H. Spohn.

Partially supported by the Academy of Finland.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bricmont, J., Kupiainen, A. Towards a Derivation of Fourier’s Law for Coupled Anharmonic Oscillators. Commun. Math. Phys. 274, 555–626 (2007). https://doi.org/10.1007/s00220-007-0284-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-007-0284-5

Keywords

Search

Navigation