Abstract
We study the family of Landau Hamiltonians on a Riemann surface S by means of a Nahm transform and an integral functor related to the Fourier-Mukai transform associated to its jacobian variety J(S). This approach allows us to explicitly determine the spectral bundles  associated to the holomorphic Landau levels. As a first main result we prove that these spectral bundles are holomorphic stable bundles with respect to the canonical polarization of J(S) determined by the theta divisor
associated to the holomorphic Landau levels. As a first main result we prove that these spectral bundles are holomorphic stable bundles with respect to the canonical polarization of J(S) determined by the theta divisor  .
.
The spectral bundles  are endowed with a natural connection
are endowed with a natural connection  and the adiabatic charge transport properties of the corresponding Landau levels are determined by the adiabatic curvature of
and the adiabatic charge transport properties of the corresponding Landau levels are determined by the adiabatic curvature of  , which coincides with the curvature of the determinant bundle det
, which coincides with the curvature of the determinant bundle det  . By means of the theory of analytic torsion and determinant bundles developed by Bismut, Gillet and Soulé we compute the adiabatic curvature of the spectral bundles on an arbitrary Riemann surface. We prove that all the holomorphic Landau levels have the same charge transport coefficients but their adiabatic curvatures differ by a term which involves the relative analytic torsion of different powers of the canonical bundle of S twisted by a fixed line bundle.
. By means of the theory of analytic torsion and determinant bundles developed by Bismut, Gillet and Soulé we compute the adiabatic curvature of the spectral bundles on an arbitrary Riemann surface. We prove that all the holomorphic Landau levels have the same charge transport coefficients but their adiabatic curvatures differ by a term which involves the relative analytic torsion of different powers of the canonical bundle of S twisted by a fixed line bundle.
Similar content being viewed by others
References
Avron, J.E., Seiler, R.: Quantization of the Hall Conductance for general, multiparticle Schrödinger Hamiltonians. Phys. Rev. Lett. 54 (4) 259–262 (1985)
Avron, J.E., Seiler, R., Yaffe, L.G.: Adiabatic theorems and applications to the quantum Hall effect. Commun. Math. Phys. 110, 33–49 (1987)
Avron, J.E., Raveh, A., Zur, B.: Adiabatic quantum transport in multiply connected systems. Rev. Mod. Phys. 60 (4), 873–915 (1988)
Avron, J.E.: Adiabatic quantum transport. In: Bregola, M., Marmo, G., Morandi, G. (eds.), Anomalies, phases, defects . . . . Lect. Int. Sch. Ferrara 1989, Napoli: Bibliopolis, 1990, pp. 9–82
Avron, J.E., Seiler, R., Zograf, P.G.: Adiabatic quantum transport: Quantization and fluctuations. Phys. Rev. Lett. 73 (24), 3255–3257 (1994)
Avron, J.E.: Adiabatic quantum transport. In: Akkermans, E., Montambaux, G., Pichard, J.L., Zinn-Justin, J. Mesoscopic quantum physics. Proceedings, Les Houches 1994. Amsterdam: Elsevier, 1995, pp. 741–791
Bartocci, C., Bruzzo, U., Hernández Ruipérez, D.: Fourier-Mukai transform and index theory. Manuscr. Math. 85, 141–163 (1994)
Birkenhake, C., Lange, H.: Complex tori, PM 177. Boston: Birkhäuser, 1999
Bismut, J.M.: The Atiyah-Singer index theorem for families of Dirac operators: two heat equation proofs. Invent. Math. 83, 91–151 (1986)
Bismut, J.M., Gillet, H., Soulé, C.: Analytic torsion and holomorphic determinant bundles I. Bott-Chern forms and analytic torsion. Commun. Math. Phys. 115, 49–78 (1988)
Bismut, J.M., Gillet, H., Soulé, C.: Analytic torsion and holomorphic determinant bundles II. Direct images and Bott-Chern forms. Commun. Math. Phys. 115, 79–126 (1988)
Bismut, J.M., Gillet, H., Soulé, C.: Analytic torsion and holomorphic determinant bundles III. Quillen metrics and holomorphic determinants. Commun. Math. Phys. 115, 301–351 (1988)
Bost, J.B.: Fibrés déterminants, déterminants régularisés et mesures sur les espaces de modules des courbes complexes. Séminaire Bourbaki 1986–87, Astérisque 152–153, 113–149 (1988)
Donaldson, S.K., Kronheimer, P.B.: The geometry of four manifolds. Oxford: Clarendon Press, 1991
Ein, L., Lazarsfeld, R.: Stability and restrictions of Picard bundles, with an application to the normal bundles of elliptic curves. In: Ellingsrud, G., Peskine, C., Sacchiero, G., Strømme, S. A. (eds.), Complex Projective Geometry (Trieste, 1989 / Bergen, 1989). Cambridge: London Math. Soc. Lecture Note Ser. 179, Cambridge: Cambridge University Press, 1992, pp. 149–156
Fay, J.: Kernel functions, analytic torsion, and moduli spaces. Mem. Amer. Math. Soc. 96, no. 464, Providence, RI: AMS 1992
García-Prada, O., Hernández Ruipérez, D., Pioli, F., Tejero Prieto, C.: Fourier-Mukai and Nahm transforms for holomorphic triples on elliptic curves. J. Geom. Phys., 55, 353–384 (2005)
Griffiths, P., Harris, J.: Principles of algebraic geometry. New York: John Wiley & Sons, 1978
Hartshorne, R.: Residues and duality. Berlin: Lecture Notes in Mathematics 20, Berlin-Heidelberg-New York: Springer-Verlag, 1966
Hartshorne, R.: Algebraic geometry. GTM 52: New York-Heidelberg, Springer-Verlag, 1977
Jardim, M.: A survey on Nahm transform. J. Geom Phys. 52, 313–327 (2004)
Kato, T.: On the adiabatic theorem of quantum mechanics. J. Phys. Soc. Japan 5, 435–439 (1950)
Kempf, G.R.: A problem of Narasimhan. Contemp. Math. 136, 283–286 (1992)
Klein, M., Seiler, R.: Power-law corrections to the Kubo formula vanish in quantum Hall systems. Commun. Math. Phys. 128, 141–160 (1990)
Knudsen, F.F., Mumford, D.: The projectivity of the moduli space of stable curves I. Preliminaries on ``det'' and ``Div''. Math. Scand. 39, 19–55 (1976)
Kobayashi, S.: Differential geometry of complex vector bundles. Princeton: Princeton University Press, 1987
Kohmoto, M.: Topological invariants and the quantization of the Hall conductance. Ann. Phys. 160, 343–354 (1985)
Lange, H., Birkenhake, C.: Complex Abelian varieties. Berlin: Springer-Verlag, 1992
Mateos Guilarte, J., Porras, J.M., de la Torre Mayado, M.: Elliptic theta functions and the fractional quantum Hall effect. J. Geom. Phys. 27, 297–332 (1997)
Mukai, S.: Duality between D(X) and
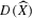 with its application to Picard sheaves. Nagoya Math. J. 81, 153–175 (1981)
with its application to Picard sheaves. Nagoya Math. J. 81, 153–175 (1981)Mukai, S.: Fourier functor and its application to the moduli of bundles on an abelian variety. Adv. Pure Math. 10, 515–550 (1987)
Niu, Q., Thouless, D.J.: Nonlinear corrections to the quantization of Hall conductance. Phys. Rev. B 30, 3561–3562 (1984)
Niu, Q., Thouless, D.J., Wu, Y-S.: Quantized Hall conductance as a topological invariant. Phys. Rev. B 31, 3372–3377, (1985)
Pioli, F.: Funtori integrali e fasci di Picard su varietà jacobiane e di Prym. Tesi di Dottorato, consorzio Genova-Torino, Ciclo IX, 1999
Quillen, D.: Determinants of Cauchy-Riemann operators on Riemann surfaces. Funct. Anal. Appl. 19, 31–34 (1986)
Ray, D.B., Singer, I.M.: R-Torsion and the Laplacian on Riemannian manifolds. Adv. Math. 7, 145–210 (1971)
Ray, D.B., Singer, I.M.: Analytic torsion for complex manifolds. Ann. Math. 98, 154–177 (1973)
Richter, T., Seiler, R.: Geometric properties of transport in quantum Hall systems. In: Gausterer, H., Grosse, H., Pittner, L. (eds.), Geometry and quantum physics. Proceedings, Schladming, 1999. Lecture Notes in Phys. 543, Berlin: Springer-Verlag, 2000, pp. 275–310
Śniatycki, J.: Geometric quantization and quantum mechanics. New York-Berlin: Springer-Verlag, 1980
Tejero Prieto, C.: Quantization of a rigid body in a magnetic monopole. Diff. Geom. and Appl. 14, 157–179 (2001)
Tejero Prieto, C.: Holomorphic spectral geometry of magnetic Schrödinger operators on Riemann surfaces. Diff. Geom. and Appl. in press
Thouless, D.J., Kohmoto, M., Nightingale, M.P., den Nijs, M.: Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49 (6), 405–408 (1982)
Varnhagen, R.: Topology and fractional quantum Hall effect. Nucl. Phys. B 443, 501–515 (1995)
Woodhouse, N.: Geometric quantization. Oxford: Clarendon Press, 1992
Wu, Y.: Quantization of a particle in a background Yang-Mills field. J. Math. Phys. 39, 867–875 (1998)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by B. Simon
Rights and permissions
About this article
Cite this article
Prieto, C. Fourier-Mukai Transform and Adiabatic Curvature of Spectral Bundles for Landau Hamiltonians on Riemann Surfaces. Commun. Math. Phys. 265, 373–396 (2006). https://doi.org/10.1007/s00220-006-1548-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-006-1548-1



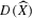 with its application to Picard sheaves. Nagoya Math. J. 81, 153–175 (1981)
with its application to Picard sheaves. Nagoya Math. J. 81, 153–175 (1981)