Abstract
We prove that for any non-trivial product-type action α of SU
q
(n) (0<q<1) on an ITPFI factor N, the relative commutant  is isomorphic to the algebra L
∞(
is isomorphic to the algebra L
∞( ) of bounded measurable functions on the quantum flag manifold
) of bounded measurable functions on the quantum flag manifold  . This is equivalent to the computation of the Poisson boundary of the dual discrete quantum group
. This is equivalent to the computation of the Poisson boundary of the dual discrete quantum group  . The proof relies on a connection between the Poisson integral and the Berezin transform. Our main technical result says that a sequence of Berezin transforms defined by a random walk on the dominant weights of SU(n) converges to the identity on the quantum flag manifold.
. The proof relies on a connection between the Poisson integral and the Berezin transform. Our main technical result says that a sequence of Berezin transforms defined by a random walk on the dominant weights of SU(n) converges to the identity on the quantum flag manifold.
Similar content being viewed by others
References
Accardi, L., Cecchini, C.: Conditional expectations in von Neumann algebras and a theorem of Takesaki. J. Funct. Anal. 45, 245–273 (1982)
Berezin, F.A.: General concept of quantization. Commun. Math. Phys. 40, 153–174 (1975)
Biane, Ph.: Marches de Bernoulli quantiques. In: Séminaire de Probabilités, XXIV, 1988/89, Lecture Notes in Math. 1426, Berlin: Springer, 1990, pp. 329–344
Biane, Ph.: Équation de Choquet-Deny sur le dual d'un groupe compact. Probab. Theory Related Fields 94, 39–51 (1992)
Biane, Ph.: Théorème de Ney-Spitzer sur le dual de SU(2). Trans. Amer. Math. Soc. 345, 179–194 (1994)
Boca, F.P.: Ergodic actions of compact matrix pseudogroups on C*-algebras. In: Recent advances in operator algebras (Orléans, 1992). Astérisque No. 232, 93–109 (1995)
Collins, B.: Martin boundary theory of some quantum random walks. Ann. Inst. H. Poincaré Probab. Statist. 40, 367–384 (2004)
Dijkhuizen, M.S., Stokman, J.V.: Quantized flag manifolds and irreducible *-representations. Commun. Math. Phys. 203, 297–324 (1999)
Duffield, N.G.: Classical and thermodynamic limits for generalized quantum spin systems. Commun. Math. Phys. 127, 27–39 (1990)
Hayashi, T.: Harmonic function spaces of probability measures on fusion algebras. Publ. Res. Inst. Math. Sci. 36, 231–252 (2000)
Helgason, S.: Differential geometry, Lie groups, and symmetric spaces. Graduate Studies in Mathematics 34, Providence, RI: Amer. Math. Soc., 2001. xxvi+641 pp.
Hiai, F., Izumi, M.: Amenability and strong amenability for fusion algebras with applications to subfactor theory. Internat. J. Math. 9, 669–722 (1998)
Høegh-Krohn, R., Landstad, M.B., Størmer, E.: Compact ergodic groups of automorphisms. Ann. of Math. (2) 114, 75–86 (1981)
Izumi, M.: Non-commutative Poisson boundaries and compact quantum group actions. Adv. Math. 169, 1–57 (2002)
Izumi, M.: Non-commutative Poisson boundaries. In: Discrete geometric analysis, Contemp. Math. 347, Providence, RI: Amer. Math. Soc., 2004, pp. 69–81
Kemeny, J.G., Snell, J.L., Knapp, A.W.: Denumerable Markov chains. Princeton, NJ-Toronto-London: D. Van Nostrand Co., Inc., 1966. xi+439 pp.
Kaimanovich, V.A.: Bi-harmonic functions on groups. C. R. Acad. Sci. Paris Sér. I Math. 314, 259–264 (1992)
Klimyk, A., Schmüdgen, K.: Quantum groups and their representations. Texts and Monographs in Physics. Berlin: Springer-Verlag, 1997. xx+552 pp.
Korogodski, L.I., Soibelman, Y.S.: Algebras of functions on quantum groups. Part I. Mathematical Surveys and Monographs 56. Providence, RI: Amer. Math. Soc. 1998. x+150 pp.
Landsman, N.P.: Strict quantization of coadjoint orbits. J. Math. Phys. 39, 6372–6383 (1998)
Neshveyev, S., Tuset, L.: The Martin boundary of a discrete quantum group. J. Reine Angew. Math. 568, 23–70 (2004)
Neshveyev, S., Tuset, L.: Quantum random walks and their boundaries. In: Analysis of (Quantum) Group Actions on Operator Algebras (Kyoto, 2003),
 1332, 57–70 (2003)
1332, 57–70 (2003)Noumi, M., Yamada, H., Mimachi, K.: Finite-dimensional representations of the quantum group
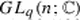 and the zonal spherical functions on U
q
(n-1)\U
q
(n). Japan. J. Math. (N.S.) 19, 31–80 (1993)
and the zonal spherical functions on U
q
(n-1)\U
q
(n). Japan. J. Math. (N.S.) 19, 31–80 (1993)Perelomov, A.: Generalized coherent states and their applications. Texts and Monographs in Physics. Berlin: Springer-Verlag, 1986. xii+320 pp.
Petz, D.: Sufficiency of channels over von Neumann algebras. Quart. J. Math. Oxford Ser. 39(2), 97–108 (1988)
Pimsner, M., Popa, S.: Entropy and index for subfactors. Ann. Sci. École Norm. Sup. 19(4), 57–106 (1986)
Podkolzin, G.B., Vainerman, L.I.: Quantum Stiefel manifold and double cosets of quantum unitary group. Pacific J. Math. 188, 179–199 (1999)
Revuz, D.: Markov chains. North-Holland Mathematical Library, Vol. 11. Amsterdam-Oxford: North-Holland Publishing Co. New York: American Elsevier Publishing Co., Inc., 1975. x+336 pp.
Rieffel, M.A.: Matrix algebras converge to the sphere for quantum Gromov–Hausdorff distance. Mem. Amer. Math. Soc. 168(796), 67–91 (2004)
Sawin, S.: Relative commutants of Hecke algebra subfactors. Amer. J. Math. 116, 591–604 (1994)
Sawin, S.: Subfactors constructed from quantum groups. Amer. J. Math. 117, 1349–1369 (1995)
Vaes, S.: Strictly outer actions of groups and quantum groups. J. Reine Angew. Math. 578, 147–184 (2005)
Woronowicz, S.L.: Compact quantum groups. In: Symétries quantiques (Les Houches, 1995), Amsterdam: North-Holland, 1998, pp. 845–884
Želobenko, D.P.: Compact Lie groups and their representations. Translations of Mathematical Monographs, Vol. 40. Providence, R.I.: Amer. Math. Soc. 1973. viii+448 pp.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Y. Kawahigashi
Supported by JSPS.
Partially supported by the Norwegian Research Council.
Supported by the SUP-program of the Norwegian Research Council.
Rights and permissions
About this article
Cite this article
Izumi, M., Neshveyev, S. & Tuset, L. Poisson Boundary of the Dual of SU q (n). Commun. Math. Phys. 262, 505–531 (2006). https://doi.org/10.1007/s00220-005-1439-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-005-1439-x




 1332, 57–70 (2003)
1332, 57–70 (2003)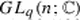 and the zonal spherical functions on U
q
(n-1)\U
q
(n). Japan. J. Math. (N.S.) 19, 31–80 (1993)
and the zonal spherical functions on U
q
(n-1)\U
q
(n). Japan. J. Math. (N.S.) 19, 31–80 (1993)