Abstract
Let A ∈ SL(n,ℝ). We show that for all n>2 there exist dimensional strictly positive constants C n such that

where ||A|| denotes the operator norm of A (which equals the largest singular value of A), ρ denotes the spectral radius, and the integral is with respect to the Haar measure on O n , normalized to be a probability measure. The same result (with essentially the same proof) holds for the unitary group U n in place of the orthogonal group. The result does not hold in dimension 2. This answers questions asked in [3, 5, 4]. We also discuss what happens when the integral above is taken with respect to measure other than the Haar measure.
Similar content being viewed by others
References
Avila, A., Bochi, J.: A formula with some applications to the theory of Lyapunov exponents. Israel J. Math. 131, 125–137 (2002)
Brualdi, R., Mellendorf, S.: Regions in the complex plane containing the eigenvalues of a matrix. Am. Math. Monthly 10, 975–985 (1994)
Burns, K., Pugh, C., Shub, M., Wilkinson, A.: Recent results about stable ergodicity. Proc. Symposia AMS 69, 327–366 (2001)
Dedieu, J-P., Shub, M.: On random and mean exponents for unitarily invariant and probability measures on
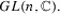 Technical report, IBM, 2001. http://www.research.ibm.com/people/s/shub/Dedieu-Shub.pdf, 2001
Technical report, IBM, 2001. http://www.research.ibm.com/people/s/shub/Dedieu-Shub.pdf, 2001Ledrappier, F., Simo, C., Shub, M., Wilkinson, A.: Random versus deterministic exponents in a rich family of diffeomorphisms. J. Stat. Phys. to appear
Hardy, H.G., Littlewood, J., Polya, G.: Inequalities. 2nd Edition, Cambridge: Cambridge University Press, 1988
Horn, R., Johnson, C.R.: Matrix Analysis. Corrected reprint, Cambridge: Cambridge University Press, England, 1990
Kato, T.: Perturbation Theory for Linear Operators. Reprint of the 1980 edition, Berlin Heidelberg-New York: Springer, 1995
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by P. Sarnak
The author is supported by the NSF DMS.
Acknowledgement The author would like to thank Amie Wilkinson for bringing the question to his attention.
Rights and permissions
About this article
Cite this article
Rivin, I. On Some Mean Matrix Inequalites of Dynamical Interest. Commun. Math. Phys. 254, 651–658 (2005). https://doi.org/10.1007/s00220-004-1282-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-004-1282-5



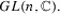 Technical report, IBM, 2001.
Technical report, IBM, 2001.