Natural orbitals of the ground state of the two-electron harmonium atom

Abstract

The radial components of the natural orbitals (NOs) pertaining to the $^1S_+$ ground state of the two-electron harmonium atom are found to satisfy homogeneous differential equations at the values of the confinement strength $\omega$ at which the respective correlation factors are given by polynomials. Together with the angular momentum l of the NOs, the degrees of these polynomials determine the orders of the differential equations, eigenvalues of which (arising from well-defined boundary conditions) yield the natural amplitudes. In the case of $l=0$, analysis of these equations uncovers certain properties of the NOs whereas application of a WKB-like approximation produces asymptotic expressions for both the NOs and the corresponding natural amplitudes that hold when the latter are small negative numbers. Extensive numerical calculations reveal that these expressions remain valid for arbitrary values of $\omega$. The approximate s-type NOs, which are remarkably accurate at sufficiently small radial distances and exhibit universal scaling, differ qualitatively from the eigenfunctions of the core Hamiltonian even at the $\omega \rightarrow \infty$ limit of vanishing electron correlation.

1 Introduction

The time-independent Schrödinger equation with the Hamiltonian

$$ \hat{H} =-\frac{1}{2} \left( \hat{\nabla }_1^2+\hat{\nabla }_2^2\right) +\frac{1}{2} \, \omega ^2 \, \left( r_1^2+r_2^2\right) +\frac{1}{r_{12}} $$

(1)

possesses closed-form solutions for infinitely many values of the confinement strength $\omega$ [1]. For this reason, the nonrelativistic system it describes, known as the two-electron harmonium atom, is often employed as a benchmarking tool in testing of approximate electronic structure methods, including those based on the density functional theory [2,3,4,5,6,7,8,9,10,11,12] and other formalisms [13,14,15,16]. Thanks to realistic electron densities involved, such tests are more suitable for calibration of density functionals and assessment of their accuracy than those relying on the homogeneous electron gas.

Electronic properties of the two-electron harmonium atom are readily elucidated not only at select values of $\omega$ but also at the weak- and strong-correlation limits. Within the former regime, which corresponds to strong confinement, the Hamiltonian (1) describes a system of two weakly coupled three-dimensional harmonic oscillators that is amenable to perturbative treatment [17,18,19,20,21,22]. On the other hand, the strongly correlated species that ensues at small values of $\omega$ can be regarded as a classical Wigner molecule subject to minor quantum corrections [17, 23].

In this paper, some recently derived properties of natural orbitals (NOs) and their occupation numbers pertaining to the $^1S_+$ ground state of the two-electron harmonium atom are reported. Although this state has been the subject of numerous studies involving both rigorous mathematical analysis [1, 17,18,19,20,21,22,23,24,25,26,27,28,29,30] and numerical approaches [17, 28], the attention devoted to the corresponding NOs has been limited to investigations of their asymptotic behavior at the $\omega \rightarrow 0$ limit [23] and of their collective occupancies at various values of $\omega$ [24,25,26], formulation of accurate approximations to the strongly occupied NOs at $\omega = \frac{1}{2}$ and $\omega = \frac{1}{10}$ [27], and finding definitive answers [28] to the questions concerning the existence of NOs with vanishing occupation numbers [17, 29, 30]. With amelioration of this unsatisfactory state of knowledge as its objective, the present work aims at uncovering universalities in NOs and their occupation numbers that persist throughout the entire range of confinement strengths.

2 Theory

The spatial part $\Psi (\vec {r_1},\vec {r_2}) \equiv \Psi (\omega ;\vec {r_1},\vec {r_2})$ of the $^1S_+$ ground-state wavefunction of the two-electron harmonium atom reads [1, 17]

$$ \Psi \left(\vec {r_1},\vec {r_2}\right)=\exp \left[ -\frac{\omega }{2}\,\left(r_1^2+r_2^2\right) \right] g(r_{12}), $$

(2)

where the correlation factor $g(r_{12}) \equiv g(\omega ;r_{12})$ (inclusive of the normalization constant) is given by the polynomials

$$ g(\omega _k;r)=\sum _{j=0}^{k} C_{j}(\omega _k) \, r^j $$

(3)

for certain values of $\omega \in \{\omega _k\}$ ($k \ge 1$), the first four elements of the set $\{\omega _k\}$ being $\omega _1 = \frac{1}{2}$, $\omega _2 = \frac{1}{10}$, $\omega _3 = \frac{5-\sqrt{17}}{24}$, and $\omega _4 = \frac{35-3\sqrt{57}}{712}$ [1, 17]. It is worth noting that, since the ratio $C_{1}(\omega )/C_{0}(\omega )$ is fixed at $\frac{1}{2}$ by the electron-coalescence cusp condition, setting $\vec {r_1} = \vec {r_2} = 0$ in Eq. (2) yields $C_{0}(\omega _k) = \Psi (\omega _k;\vec {0},\vec {0})$ and $C_{1}(\omega _k) = \frac{1}{2} \Psi (\omega _k;\vec {0},\vec {0})$. Throughout the text, the $\{{{\mathrm{Re}}}(\Psi (\vec {0},\vec {0})) > 0, \, {{\mathrm{Im}}}(\Psi (\vec {0},\vec {0})) = 0 \}$ phase convention is employed for the wavefunction, which is assumed to be square-normalized to one.

The spatial parts $\{\psi _{nlm}(\vec {r})\} \equiv \{ \psi _{nlm}(\omega ;\vec {r})\}$ of the NOs pertaining to $\Psi (\vec {r_1},\vec {r_2})$ are eigenfunctions of a homogeneous Fredholm equation of the second kind [31]

$$ \int \Psi (\vec {r_1},\vec {r_2}) \, \psi _{nlm}( \vec {r_2}) \, \mathrm{d}\vec {r_2} = \lambda _{nl} \, \psi _{nlm} (\vec {r_1}). $$

(4)

Squares of absolute values of the respective natural amplitudes $\{\lambda _{nl}\} \equiv \{\lambda _{nl}(\omega )\}$ equal the occupation numbers $\{\nu _{nl}\} \equiv \{\nu _{nl}(\omega )\}$. Thanks to the spherical symmetry of the underlying wavefunction, the angular degrees of freedom can be integrated out from Eq. (4), yielding [compare Eq. (2)]

$$\begin{aligned}&\frac{4 \, \pi }{2\,l+1} \, \int _{0}^{\infty } \exp \left[ -\frac{\omega }{2}\,\left(r_1^2+r_2^2\right) \right] g_l(r_{1},r_{2}) \, \phi _{nl}(r_2) \, r_{2}^{2} \; \mathrm{d}r_2 \nonumber \\&\quad = \lambda _{nl} \, \phi _{nl} (r_1) \end{aligned}$$

(5)

for the NOs with the angular momenta of l [27, 30]. In Eq. (5), $\{\phi _{nl}(r)\} \equiv \{ \phi _{nl}(\omega ;r)\}$ (normalized according to $\int ^{\infty }_0 [\phi _{nl}(r)]^2 \, r^2 \; \mathrm{d}r = 1$) are the real-valued radial parts of $\{\psi _{nlm}( \vec {r})\}$,

$$ \psi _{nlm}( \vec {r}) = \phi _{nl}(r) \; Y_{l}^{m}(\theta ,\varphi), $$

(6)

and the angularly averaged correlation factor $g_l(r_1,r_2) \equiv g_l(\omega ;r_1,r_2)$ reads

$$\begin{aligned} g_l(r_1,r_2)=\, & {} \frac{2\,l+1}{2\,r_1\,r_2} \nonumber \\ &\quad \times \int _{|r_1-r_2|}^{r_1+r_2} \, P_{l}\left( \frac{r_{1}^{2}+r_{2}^{2}-r_{12}^{2}}{2\,r_{1}\,r_{2}} \right) \; g(r_{12}) \, r_{12} \; \mathrm{d}r_{12}, \end{aligned}$$

(7)

where the standard notation of $Y_{l}^{m}(\theta ,\varphi )$ and $P_{l}(t)$ is used for the respective spherical harmonic and Legendre polynomial.

2.1 A differential equation for NOs

Combining Eqs. (3), (5), and (7) affords

$$\begin{aligned}&2 \, \pi \, \int _{0}^{r_1} \exp \left( -\omega _k \, r_2^2 \right) \left[ \; \sum _{j=0}^{k} C_{kj} \, U_{lj}(r_1,r_2) \, \right] \chi _{knl}(r_2) \; \mathrm{d}r_2 \nonumber \\&\quad +\, 2 \, \pi \, \int _{0}^{\infty } \exp \left( -\omega _k \, r_2^2 \right) \left[ \; \sum _{j=0}^{k} C_{kj} \, W_{lj}(r_1,r_2) \, \right] \chi _{knl}(r_2) \; \mathrm{d}r_2 \nonumber \\&\quad \quad =\lambda _{knl} \; r_{1}^{2l} \, \chi _{knl} (r_1), \end{aligned}$$

(8)

where the eigenfunctions $\{ \chi _{knl}(r) \} \equiv \{ \chi _{nl}(\omega _k;r) \}$ are related to the spatial parts of NOs through the equation

$$ \chi _{knl}(r)=\exp \left( \frac{\omega _k}{2} \, r^2\right) r^{1-l} \; \phi _{nl}(\omega _k;r). $$

(9)

Here and in the following, the notation $C_{kj} \equiv C_{j}(\omega _k)$ and $\lambda _{knl} \equiv \lambda _{nl}(\omega _{k})$ is employed for the sake of convenience, whereas the standard notation of $P_{l}^{(q)}(t)$ is used for the qth derivative of the respective Legendre polynomial in the definitions

$$\begin{aligned}&U_{lj}(r_1,r_2)=\,\left[ (-1)^{j}-1 \right] \; \sum _{q=0}^{l} \frac{(-\frac{1}{2})^q \; (r_1 \, r_2)^{l-q}}{(j+2q+2) \, q!}\nonumber \\ &\quad \times P_{l}^{(q)} \Big (\frac{r_{1}^{2}+r_{2}^{2}}{2\,r_{1}\,r_{2}} \Big ) (r_1-r_2)^{j+2q+2} \end{aligned}$$

(10)

and

$$\begin{aligned}&W_{lj}(r_1,r_2)= \sum _{q=0}^{l} \frac{(-\frac{1}{2})^q \; (r_1 \, r_2)^{l-q}}{(j+2q+2) \, q!}\nonumber \\ &\quad \times P_{l}^{(q)} \Big (\frac{r_{1}^{2}+r_{2}^{2}}{2\,r_{1}\,r_{2}} \Big ) \left[ \, (r_1+r_2)^{j+2q+2}-(r_2-r_1)^{j+2q+2} \, \right] \; . \end{aligned}$$

(11)

As the sums over j in the l.h.s. of Eq. (8) are polynomials of degree$2l+2 \, [\frac{k+1}{2}]+1$ in $r_1$ (here and in the following, [t] denotes the integer part of t), differentiating both sides of this equation $2l+2 \, [\frac{k+1}{2}]+2$ times with respect to $r_1$ produces a homogeneous differential equation for $\chi _{knl} (r)$ that reads

$$\begin{aligned}&2 \, \pi \, \left( \frac{\partial }{\partial r_1} \right) ^{2l+2 \, [\frac{k+1}{2}]+2} \int _{0}^{r_1} \exp \left( -\omega _{k} \, r_2^2 \right) \left[ \; \sum _{j=0}^{k} C_{kj} \, U_{lj}(r_1,r_2) \, \right] \chi _{knl}(r_2) \; \mathrm{d}r_2 = \lambda _{knl} \; \left( \frac{\partial }{\partial r_1} \right) ^{2l+2 \, [\frac{k+1}{2}]+2} \left[ r_{1}^{2l} \, \chi _{knl} (r_1) \right]. \end{aligned}$$

(12)

Together with $2l+2 \, [\frac{k+1}{2}]+2$ boundary conditions

$$\begin{aligned}&2 \, \pi \, \left( \frac{\partial }{\partial r_1} \right) ^p \; \Bigg ( r_{1}^{-2l} \, \int _{0}^{r_1} \exp \left( -\omega _{k} \, r_2^2 \right) \left[ \; \sum _{j=0}^{k} C_{kj} \, U_{lj}(r_1,r_2) \, \right] \chi _{knl}(r_2) \; \mathrm{d}r_2 \nonumber\\ &\qquad+ \, r_{1}^{-2l} \, \int _{0}^{\infty } \exp \left( -\omega _{k} \, r_2^2 \right) \left[ \; \sum _{j=0}^{k} C_{kj} \, W_{lj}(r_1,r_2) \, \right] \chi _{knl}(r_2) \; \mathrm{d}r_2 \Bigg ) \; \Bigg |_{r_{1}=0} \nonumber\\ &\quad= \lambda _{knl} \; \chi _{knl}^{(p)} (0), \quad p =0, \, \dots , 2l+2 \, \left[ \frac{k+1}{2}\right] +1, \end{aligned}$$

(13)

this eigenequation is fully equivalent to Eq. (8).

There are $l+ \, [\frac{k+1}{2}]+1$ conditions (13) corresponding to even p that simply imply vanishing of $\chi _{knl} (r)$ and all its even-order derivatives at $r=0$. The remaining $l+ \, [\frac{k+1}{2}]+1$ conditions that ensue for odd p are rather cumbersome. However, satisfying them is equivalent to enforcing the large-r asymptotics of $\chi _{knl}(r) \xrightarrow [r \rightarrow \infty ] \, \chi _{knl}^{>}(r)+o(1)$, where the rational function

$$\begin{aligned}&\chi _{knl}^{>} (r_1) = \frac{2 \, \pi }{ \lambda _{knl}} \; r_{1}^{-2l} \, \int _{0}^{\infty } \exp \left( -\omega _k \, r_2^2 \right) \nonumber \\ &\quad\qquad\quad\times \sum _{j=0}^{k} C_{kj} \, \left[ U_{lj}(r_1,r_2) \right. \nonumber \\ &\qquad\quad\quad \left. +\,W_{lj}(r_1,r_2) \right] \, \chi _{knl}(r_2) \; \mathrm{d}r_2 \end{aligned}$$

(14)

is the first member of the sequence of large-r asymptotic approximants $\{ \chi _{knl}^{>\,[q]} (r_1) \}$ defined recursively as [compare Eq. (8)]

$$\begin{aligned}&\chi _{knl}^{>\,[q+1]}(r_1) = \chi _{knl}^{>}(r_1) - \frac{2 \, \pi }{ \lambda _{knl}} \; r_{1}^{-2l} \, \int _{r_1}^{\infty } \exp \left( -\omega _k \, r_2^2 \right) \;\nonumber \\&\quad \times \sum _{j=0}^{k} C_{kj} \, U_{lj}(r_1,r_2) \, \chi _{knl}^{>\,[q]}(r_2) \; \mathrm{d}r_2. \end{aligned}$$

(15)

2.2 The case of $l=0$

For $l=0$, the differential Eq. (12) and the boundary conditions (13) assume particularly simple forms, namely

$$\begin{aligned}&-4 \, \pi \, \sum _{j=0}^{\left[ \frac{k-1}{2} \right] } \, (2j+2)! \; C_{k,2j+1} \left( \frac{\partial }{\partial r_1} \right) ^{ 2 \left[ \frac{k-1}{2} \right] - 2j } \left[ \exp \left( -\omega _{k} \, r_1^2 \right) \chi _{kn0} (r_1) \right] \; = \lambda _{kn0} \left( \frac{\partial }{\partial r_1} \right) ^{ 2 \left[ \frac{k+3}{2} \right] } \chi _{kn0} (r_1), \end{aligned}$$

(16)

together with

$$ \chi _{kn0}^{(p)} (0)=0, \quad p =0, \, 2, \, \dots , 2 \, \left[\frac{k+1}{2}\right] $$

(17)

and

$$\begin{aligned}&-4 \, \pi \, \sum _{j=0}^{\min \left( \left[ \frac{k-1}{2} \right] ,\frac{p-5}{2} \right) } \, (2j+2)! \; C_{k,2j+1} \left( \frac{\partial }{\partial r_1} \right) ^{p - 2j -4} \left[ \exp \left( -\omega _{k} \, r_1^2 \right) \chi _{kn0} (r_1) \right] \; \Bigg |_{r_{1}=0} + \, \sum _{j=\max (0,p-2)}^{k} \frac{(j+1)!}{(j+2-p)!} \; C_{kj} \; \mu _{kn0,j+2-p} = \lambda _{kn0} \, \chi _{kn0}^{(p)} (0), \quad p =1, \, 3, \, \dots , 2 \, [\frac{k+1}{2}]+1, \end{aligned}$$

(18)

where

$$ \mu _{knl,j}=4 \, \pi \int _{0}^{\infty } \exp \left( -\omega _{k} \, r^2 \right) r^{j} \; \chi _{knl} (r) \, \mathrm{d}r. $$

(19)

The large-r asymptotics becomes a polynomial (note the linear dependences among its coefficients)

$$\begin{aligned}&\chi _{kn0}^{>}(r) = \lambda _{kn0}^{-1} \, \Bigg ( \, \sum _{j=1}^{\left[ \frac{k+1}{2} \right] } \frac{1}{2j+1} \; C_{k,2j-1} \; \mu _{kn0,2j+1} \nonumber \\&\quad + \, \sum _{p=1}^{k+1} \, \frac{r^p}{p!} \, \sum _{j=0}^{\left[ \frac{k+1-p}{2} \right] } \frac{(2j+p)!}{(2j+1)!} \; C_{k,2j+p-1} \; \mu _{kn0,2j+1} \, \Bigg ) \quad \end{aligned}$$

(20)

and the approximants (15) are given by

$$\begin{aligned}&\chi _{kn0}^{>\,[q+1]}(r_1) = \chi _{kn0}^{>}(r_1) + \frac{4 \, \pi }{ \lambda _{kn0}} \, \int _{r_1}^{\infty } \exp \left( -\omega _k \, r_2^2 \right) \;\nonumber \\&\quad \times\sum _{j=0}^{\left[ \frac{k-1}{2} \right] } \frac{C_{k,2j+1}}{2j+3} \;(r_1-r_2)^{2j+3} \, \chi _{kn0}^{>\,[q]}(r_2) \; \mathrm{d}r_2. \end{aligned}$$

(21)

2.3 The s-type NOs pertaining to $\omega =\omega _1$ and $\omega =\omega _2$

For the first two instances of the explicitly known eigenfunctions of the Hamiltonian (1), the sum in the l.h.s. of Eq. (16) reduces to a single term, yielding

$$\begin{aligned}&-8 \, \pi \, C_{k1} \, \exp (-\omega _k \, r^{2}) \, \chi _{kn0}(r) = \lambda _{kn0} \, \chi ^{(4)}_{kn0}(r) ,\nonumber \\ &\quad k=1, \, 2 . \end{aligned}$$

(22)

Despite arising from the same eigenequation, the eigenfunctions $\chi _{1n0}(r)$ and $\chi _{2n0}(r)$ are not related through an argument/value scaling because of their different large-r asymptotics, namely [compare Eq. (20)]

$$ \chi _{1n0}^{>}(r) = \lambda _{1n0}^{-1} \, \Bigg ( \frac{1}{3} \; C_{11} \; \mu _{1n0,3} +C_{10} \; \mu _{1n0,1}\, r +C_{11} \; \mu _{1n0,1}\, r^2 \Bigg) $$

(23)

versus

$$\begin{aligned} \chi _{2n0}^{>}(r)=\, & {} \lambda _{2n0}^{-1} \, \Bigg ( \frac{1}{3} \; C_{21} \; \mu _{2n0,3} + (C_{20} \; \mu _{2n0,1} +C_{22} \; \mu _{2n0,3} )\, r \nonumber \\&\quad +C_{21} \; \mu _{2n0,1}\, r^2 +\, C_{22} \; \mu _{2n0,1}\, r^3 \Bigg). \end{aligned}$$

(24)

It should be emphasized that none of the NOs can be unoccupied as setting $\lambda _{kn0} =0$ in Eq. (22) would imply vanishing of $\chi _{kn0}(r)$ for all r. On the other hand, integration of this eigenequation subject to the boundary conditions (17) produces

$$\begin{aligned} \chi ^{(2)}_{kn0}(r)=\, & {} \chi ^{(3)}_{kn0}(0) \, r-8 \, \pi \, \lambda _{kn0}^{-1} \,C_{k1} \nonumber\\ &\quad\times \int _0^r \, \chi _{kn0}(r')\nonumber \\&\quad \,\exp (-\omega _k \, r'^{2}) \, (r-r') \; \mathrm{d}r' \; , \end{aligned}$$

(25)

allowing for elucidation of some properties of the NOs. To achieve this goal, one conveniently assumes without any loss of generality that $\chi ^{(1)}_{kn0}(0)>0$ (i.e., the respective NO is positive-valued at $r =0$) and notes that $C_{k1} > 0$. Inspection of Eq. (25) leads to the conclusion that the combination of $\chi ^{(3)}_{kn0}(0)>0$ and $\lambda _{kn0} < 0$ assures $\chi ^{(2)}_{kn0}(r)$ being positive-valued for $r > 0$ and thus $\chi ^{(1)}_{kn0}(r)$ being both positive-valued and strictly increasing with r as long as $\chi _{kn0}(r) \ge 0$. As vanishing of $\chi _{kn0}(r_0)$ at some $r_0 > 0$ [note that $\chi _{kn0}(0)=0$ per the boundary conditions (17)] would contradict these findings, the corresponding NO must be nodeless and the moments $\{ \mu _{kn0,j} \}$ must be positive-valued for all j.

For $\omega =\omega _1$, the boundary conditions (18) become

$$ \chi ^{(1)}_{1n0}(0)=\lambda _{1n0}^{-1} \left( C_{10} \, \mu _{1n0,1}+C_{11} \, \mu _{1n0,2} \right) $$

(26)

and

$$ \chi ^{(3)}_{1n0}(0)=2 \, \lambda _{1n0}^{-1} \, C_{11} \, \mu _{1n0,0}. $$

(27)

Since both the coefficients $C_{10}$ and $C_{11}$ are positive-valued, one infers from Eq. (26) that at least one of the moments that enters its r.h.s. has to have the same sign as $\lambda _{1n0}$. Consequently, all the NOs pertaining to negative-valued natural amplitudes must possess nodes and thus, per the considerations of the preceding paragraph and the boundary condition (27), the corresponding third-order derivatives $\{ \chi ^{(3)}_{kn0}(0) \}$ must be negative-valued and the moments $\{ \mu _{1n0,0} \}$ must be greater than zero. On the other hand, nothing precludes the existence of a nodeless NO pertaining to a positive-valued natural amplitude. However, due to the orthonormality of the NOs, only one such natural orbital [characterized by $\chi ^{(3)}_{kn0}(0) >0$] is possible.

All of those inferences carry over to the case of $\omega =\omega _2$, where the boundary conditions (26) and (27) are replaced with

$$ \chi ^{(1)}_{2n0}(0)=\lambda _{2n0}^{-1} \left( C_{20} \, \mu _{2n0,1}+C_{21} \, \mu _{2n0,2}+C_{22} \, \mu _{2n0,3} \right) $$

(28)

and

$$ \chi ^{(3)}_{2n0}(0)=2 \, \lambda _{2n0}^{-1} \left( C_{21} \, \mu _{2n0,0}+3 \, C_{22} \, \mu _{2n0,1} \right), $$

(29)

the coefficients $C_{20}$, $C_{21}$, and $C_{22}$ again being all positive-valued.

2.4 Approximate solutions of Eq. (16)

For negative-valued natural amplitudes, applying a WKB-like approximation [32] to Eq. (16) yields the (unnormalized) eigenfunctions

$$\begin{aligned} \chi _{kn0}(r)\approx & {} \left( \frac{4 \,\omega _k}{\pi } \right) ^{1/4} \exp \left( \frac{3 \, \omega _k}{8} \, r^{2} \right) \nonumber \\&\quad \Bigg \{ \sin \left[ \pi \, \beta _{kn0} \; {{\mathrm{erf}}}\left( \frac{\sqrt{\omega _k}}{2} \; r \right) \right] \nonumber \\&\quad +\, A_{kn0} \, \sinh \left[ \pi \, \beta _{kn0} \; {{\mathrm{erf}}}\left( \frac{\sqrt{\omega _k}}{2} \; r \right) \right] \Bigg \}, \end{aligned}$$

(30)

where

$$ \beta _{kn0}= \left( -\,\frac{8 \, C_{k1}}{\pi \, \omega _{k}^{2} \, \lambda _{kn0}} \right) ^{1/4} $$

(31)

[note that the other two linearly independent approximate solutions that involve the cos and cosh functions do not enter Eq. (30) because of the vanishing of $\chi _{kn0}(0)$ and $\chi _{kn0}^{(2)}(0)$ required by the boundary conditions (17)]. The small-r approximation (30) is asymptotically exact at the $\lambda _{kn0} \rightarrow 0$ limit and is expected to be accurate for r satisfying the inequality $\exp (\omega _k \, r^2) \ll \beta _{kn0}^4$.

In principle, an approximation valid throughout the entire range of radial distances could be obtained by stitching the above result with the large-r asymptotics given by Eq. (20). However, the resulting quantization of the natural amplitudes turns out to be unduly sensitive to the choice of the stitching point, rendering such an approach impractical. Instead, one can either set $A_{kn0}$ to zero or determine it by matching the radial location of the outermost node of the approximant (30) with that of its exact counterpart. When employed in conjunction with exact natural amplitudes, either of those choices produced NOs of remarkable accuracy (see the next section of this paper).

The large-r asymptotics of the approximant (30) is not compatible with the polynomial (20) unless the latter is set to zero. In that case, one obtains

$$ A_{kn0} = - \frac{\sin \pi \beta _{kn0}}{\sinh \pi \beta _{kn0}} $$

(32)

and

$$ \frac{\tan \pi \beta _{kn0}}{\tanh \pi \beta _{kn0}}=1, $$

(33)

i.e., an approximate quantization of the negative-valued natural amplitudes $\{ \lambda _{kn0} \}$. Equation (33) admits infinitely many positive-valued solutions, all of which are very close to $n+\frac{1}{4} \, (n=1,2, \dots )$. When substituted into Eq. (32), these solutions produce the coefficients $\{A_{kn0} \}$ whose rapid decay with n follows the asymptotics of $(-1)^{n+1} \, \sqrt{2} \, \exp [-\pi (n+\frac{1}{4})]$. In light of these facts, one expects the quantity $\Delta _{kn0}$ in the expression

$$\begin{aligned} \lambda _{kn0}=\, & {} - \frac{8 \, C_{k1}}{\pi \, \omega _{k}^2} \; (n+\Delta _{kn0})^{-4} \nonumber \\=\, & {} - \frac{4 \, \Psi (\omega _k;\vec {0},\vec {0})}{\pi \, \omega _{k}^2} \; (n+\Delta _{kn0})^{-4} \quad \end{aligned}$$

(34)

to be small and dependent on n only weakly.

Setting $A_{kn0}=0$ in Eq. (30), which implies setting $\Delta _{kn0}=1$ in Eq. (34) [required by suppression of the leading divergence of $\chi _{n0}(\omega _k;r)$ at $r \rightarrow \infty$], affords a primitive approximation,

$$\begin{aligned} \phi _{n0}(\omega _k;r)\approx & {} \left( \frac{4 \,\omega _k}{\pi } \right) ^{1/4} \exp \left( - \frac{\omega _k}{8} \, r^{2} \right) \, r^{-1} \nonumber \\&\quad \times \sin \left[ \pi \, (n+1) \, {{\mathrm{erf}}}\left( \frac{\sqrt{\omega _{k}}}{2} \, r \right) \right] \, , \end{aligned}$$

(35)

to the radial part $\phi _{n0}(\omega _k;r)$ of the natural orbital pertaining to the natural amplitude $\lambda _{kn0}$ (note the presence of n radial nodes). Although the approximants (35) are rather inaccurate, for a given $\omega _k$ they form a set of orthonormal functions whose simplicity facilitates evaluation of asymptotic expressions for matrix elements of one-electron operators. In particular, one obtains

$$\begin{aligned} t_{kn0} &\equiv t_{n0}(\omega _k) \nonumber \\ &= {} \Big \langle \psi _{n00}(\omega _k;\vec r) \Big |\nonumber \\ &\quad \quad -\frac{1}{2} \, \hat{\nabla }^2\, \Big |\psi _{n00}(\omega _k;\vec r) \Big \rangle \xrightarrow [n \rightarrow \infty ]{} \frac{\sqrt{3}}{6} \, \pi \, \omega _k \, n^2 \quad \end{aligned}$$

(36)

and

$$\begin{aligned} v_{kn0}\equiv \, & {} v_{n0}(\omega _k) \nonumber \\=\, & {} \Big \langle \psi _{n00}(\omega _k;\vec r) \Big |\,\frac{1}{2} \, \omega _k^2 \, r^2 \,\Big |\psi _{n00}(\omega _k;\vec r) \Big \rangle \xrightarrow [n \rightarrow \infty ]{} \omega _k. \end{aligned}$$

(37)

In turn, combining Eqs. (34), (36), and (37) with the alternative expression for the natural amplitudes, which reads [28]

$$ \lambda _{kn0} = \frac{\eta _{kn0}}{E_k - 2 \, h_{kn0}}, $$

(38)

where

$$ \eta _{kn0} \equiv \eta _{n0}(\omega _k) = \Big \langle \psi _{n00}(\omega _k;\vec r_1) \Big |\,\frac{ \Psi (\omega _k;\vec {r_1},\vec {r_2})}{r_{12}} \, \Big |\psi _{n00}(\omega _k;\vec r_2) \Big \rangle, $$

(39)

$E_k \equiv E(\omega _k) =\langle \Psi (\omega _k;\vec {r_1},\vec {r_2})|\hat{H}|\Psi (\omega _k;\vec {r_1},\vec {r_2})\rangle$, and $h_{kn0} \equiv h_{n0}(\omega _k) = t_{n0}(\omega _k) + v_{n0}(\omega _k)$, produces the asymptotics

$$ \eta _{kn0} \xrightarrow [n \rightarrow \infty ]{} \frac{8 \, C_{k1}}{\sqrt{3} \, \omega _{k}} \; n^{-2}. $$

(40)

3 Numerical verification of theoretical predictions

Numerical algorithms for computation of highly accurate energies $E(\omega )$ and wavefunctions $\Psi (\omega ;\vec {r_1},\vec {r_2})$ together with the corresponding natural amplitudes $\{ \lambda _{nl}(\omega ) \}$ and the spatial parts $\{ \psi _{nlm}(\omega ;\vec {r}) \}$ of the natural orbitals for arbitrary finite values of the confinement strength $\omega$ have been described in detail elsewhere [28]. At the $\omega \rightarrow \infty$ limit, these algorithms are superseded by a simplified treatment based upon perturbation theory [25] that involves evaluation of the elements

$$\begin{aligned}&G_{l,pq}=-\left( \frac{2}{\pi } \right) ^{1/2} \; 2^{4-(2p+2q+l)} \, \frac{(2p+2q+2l-5)!}{(p+q+l-2)!} \, \nonumber \\&\quad \times \left[ \frac{(p+l-1)! \, (q+l-1)!}{(p-1)! \,(2p+2l-1)! \, (q-1)! \, (2q+2l-1)!} \right] ^{1/2} \quad \end{aligned}$$

(41)

of the matrices $\{ \varvec{G}_{l} \} \equiv \{ \{ G_{l,pq} \}_{p,q=1+\delta _{l0}}^{M} \}$ whose eigenvalues approximate the negative-valued reduced natural amplitudes $\{ \bar{\lambda }_{nl} \}$,

$$ \bar{\lambda }_{nl} =\lim _{\omega \rightarrow \infty } \omega ^{1/2} \, \lambda _{nl}(\omega), $$

(42)

and the respective eigenvectors $\{ \varvec{D}_{nl} \} \equiv \{ \{ D_{nl,q} \}_{q=1+\delta _{l0}}^{M} \}$ enter the approximants [where $L_{q-1}^{l+1/2} (t)$ is the pertinent associated Laguerre polynomial]

$$\begin{aligned}&\bar{\psi }_{nlm}(\vec {r}) \approx \, 2 \, \pi ^{-1/4} \; \sum _{q=1+\delta _{l0}}^{M} \left[ \frac{(2q-2)!!}{(2q+2l-1)!!} \right] ^{1/2} \, D_{nl,q} \nonumber \\&\quad \times \, L_{q-1}^{l+1/2} \left( r^2 \right) \, \left( 2 \, r^{2} \right) ^{l/2} \, \exp \left( -\frac{1}{2} \, r^2 \right) \; Y_{l}^{m}(\theta ,\varphi ) \quad \end{aligned}$$

(43)

for the reduced spatial parts $\{ \bar{\psi }_{nlm}(\vec {r}) \}$ of the natural orbitals defined as

$$ \bar{\psi }_{nlm}(\vec {r}) =\lim _{\omega \rightarrow \infty } \omega ^{-3/4} \, \psi _{nlm}(\omega ;\omega ^{-1/2} \, \vec {r}). $$

(44)

Computations of $\mathrm {Tr} \, \left[ \varvec{G}_{1}(\omega ) \right] ^{2}$ and $\mathrm {Tr} \, \left[ \varvec{G}_{2}(\omega ) \right] ^{2}$ by infinite algebraic summations yield the large-$\omega$ asymptotics of the collective occupancies per spin and single value of m that read, respectively, $\frac{127-48 \pi +36 \ln 2}{72 \, \pi } \; \omega ^{-1} \approx 5.11440 \cdot 10^{-3} \; \, \omega ^{-1}$ and $\frac{-2053+720 \pi -300 \ln 2}{1800 \, \pi } \; \omega ^{-1} \approx 1.77291 \cdot 10^{-4} \; \omega ^{-1}$, in agreement with the previously published estimates [17]. The numerical data of the present study that are quoted below have been calculated with 2000-digit arithmetic available within the algebraic manipulation software [33] from matrices truncated at M = 1000.

Fig. 1

The exact (black) reduced radial parts $\exp (-\frac{3 \,\omega _k}{8} \, r^2) \, \chi _{n0}(\omega _k;r)$ of the s-type NOs for $k=1$ together with the respective large-r asymptotics (20) (red) and the WKB approximants (30) with $A_{kn0}$ either set to zero (green) or obtained by matching the radial position of the outermost node (blue): (a) $n=10$, (b) $n=20$, and (c) $n=30$

Fig. 2

The exact (black) reduced radial parts $\exp (-\frac{3 \,\omega _k}{8} \, r^2) \, \chi _{n0}(\omega _k;r)$ of the s-type NOs for $k=2$ together with the respective large-r asymptotics (20) (red) and the WKB approximants (30) with $A_{kn0}$ either set to zero (green) or obtained by matching the radial position of the outermost node (blue): (a) $n=10$, (b) $n=20$, and (c) $n=30$

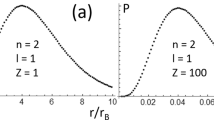
Numerical verification of the theoretical predictions formulated in the previous section of this paper commences with comparisons between the exact and approximate natural orbitals (here and in the following, the s-type NOs are ordered according to decreasing absolute magnitudes of the corresponding negative-valued natural amplitudes, with $n=1$ assigned to first such NO, etc.). Inspection of Figs. 1 and 2 reveals remarkable accuracy of the reduced radial parts [given by $\exp (-\frac{3\,\omega }{8} \, r^2) \, \chi _{n0}(\omega ;r)$ or, equivalently, $\exp (\frac{\omega }{8} \, r^2) \, r \, \phi _{n0}(\omega ;r)$] of the 10th, 20th, and 30th NOs computed from the approximants (30) at both $\omega =\frac{1}{2}$ and $\omega =\frac{1}{10}$. The excellent agreement at sufficiently small radial distances is unaffected by the choice of $A_{kn0}$ being either set to zero or determined by matching the radial location of the outermost node of the approximant with that of its exact counterpart. On the other hand, as expected, neither choice gives rise to correct asymptotics at $r \rightarrow \infty$ [which is, however, faithfully reproduced by $\exp (-\frac{3\,\omega }{8} \, r^2) \, \chi ^{>}_{kn0}(r)$]. These features of the approximants are found to carry over not only to other values of k, such as in the case of $\omega =\omega _3$ (Fig. 3a), but also to arbitrary magnitudes of the confinement strength such as $\omega =1$ (Fig. 3b) and even the $\omega \rightarrow \infty$ limit of vanishing correlation [Fig. 3c, note that $\bar{\chi }_{n0}(\bar{r}) = \lim \limits _{\omega \rightarrow \infty } \, \omega ^{-1/4} \, \chi _{n0}(\omega ;\omega ^{-1/2} \, \bar{r})$], uncovering approximate universal scaling of the s-type NOs.

Fig. 3

The exact (black) reduced radial parts $\exp (-\frac{3 \,\omega }{8} \, r^2) \, \chi _{n0}(\omega ;r)$ of the s-type NOs for $n=20$ together with the respective WKB approximants (30) with $A_{kn0}$ either set to zero (green) or obtained by matching the radial position of the outermost node (blue): (a) $\omega =\omega _3$, (b) $\omega =1$, and (c) $\omega \rightarrow \infty$ (see the text for explanation)

Two remarks are in order at this point. First of all, due to the presence of the factor of $\exp (\frac{\omega }{8}\, r^2)$, the absolute errors exhibited at larger values of r by the approximate reduced radial parts of the NOs displayed in Figs. 1, 2, and 3 are much larger than those of the actual natural orbitals. Second, as the number of nodes increases with n, the spacing between them becomes proportionally reduced, leaving the radial extents of the NOs barely changed. This observation explains the large-n asymptotic behavior of the expectation values of both the kinetic energy operator [Eq. (36)] and the operator describing the interaction with the confining potential [Eq. (37)]. The asymptotic constancy of $v_{n0}(\omega )$ with respect to n, which reflects the almost constant radial extents of the NOs, is consistent with the quadratic dependence of $t_{n0}(\omega )$ on n that is reminiscent of that known for a particle in one-dimensional box. These asymptotics are expected to persist for all values of $\omega$, including the limit of $\omega \rightarrow \infty$ at which the interelectron interaction becomes vanishingly small in comparison with the other components of the Hamiltonian (1). When juxtaposed against the linear dependences on n exhibited by the kinetic and potential energy components pertaining to the s-type wavefunctions of the three-dimensional harmonic oscillator (which become more and more diffuse upon successive excitations), these asymptotics vividly illustrate the fundamental difference between the natural orbitals and the eigenfunctions of the one-electron Hamiltonians that are left in $\hat{H}$ upon removal of the interelectron interaction term.

Fig. 4

Deviations from the large-n asymptotics of the natural amplitudes: (a) $\lambda _{kn0}$ for $k=1$ (green), $k=2$ (blue), $k=3$ (red), and $k=4$ (orange); (b) $\lambda _{nl}(\omega )$ for $\omega =1, \, l=0$ (green), $\omega \rightarrow \infty , \, l=0$ (purple), $\omega \rightarrow \infty , \, l=1$ (red), and $\omega \rightarrow \infty , \, l=2$ (orange)

Fig. 5

Deviations from the large-n asymptotics of: (a) the denominators $E_k-2 \, h_{kn0}$ and (b) the numerators $\eta _{kn0}$ for $k=1$ (green), $k=2$ (blue), $k=3$ (red), and $k=4$ (orange)

The natural amplitudes $\{ \lambda _{kn0} \}$ computed for $k=1$, $k=2$, $k=3$, and $k=4$ are found to follow the asymptotics (34) as attested by both the smallness and the weak dependence on n of the expression $\big ( -\frac{\pi \, \omega _k^2 \, \lambda _{kn0}}{8 \, C_{k1}} \big )^{-1/4}-n$ (Fig. 4a). In general, the rate at which this asymptotics is approached appears to diminish with increasing k. Quite unexpectedly, the natural amplitudes $\{ \lambda _{nl}(\omega ) \}$ computed at arbitrary values of $\omega$ and even for $l \ne 0$ turn out to exhibit the same large-n behavior (which is reflected in the values of $\big [ -\frac{\pi \, \omega ^2 \, \lambda _{nl}(\omega )}{4 \, \Psi (\omega ;\vec 0,\vec 0)} \big ]^{-1/4}-n$ plotted against n in Fig. 4b). The analogous plots of the quantities $\big [ -\frac{\sqrt{3} \; (E_k-2\;h_{kn0})}{\pi \, \omega _k} \big ]^{1/2} -n$ (Fig. 5a) and $\big ( \frac{\sqrt{3} \; \omega _k \, \eta _{kn0}}{8 \, C_{k1}} \big )^{-1/2}-n$ (Fig. 5b) confirm the predicted asymptotics (36), (37), and (40).

4 Conclusions

The radial components of the natural orbitals (NOs) pertaining to the $^1S_+$ ground state of the two-electron harmonium atom are found to satisfy homogeneous differential equations at the values of the confinement strength $\omega$ at which the respective correlation factors are given by polynomials. Together with the angular momentum l of the NOs, the degrees of these polynomials determine the orders of the differential equations, eigenvalues of which (arising from well-defined boundary conditions) yield the natural amplitudes. In the case of $l=0$, analysis of these equations uncovers certain properties of the NOs whereas application of a WKB-like approximation produces asymptotic expressions for both the NOs and the corresponding natural amplitudes that hold when the latter are small negative numbers. Extensive numerical calculations reveal that these expressions remain valid for arbitrary values of $\omega$. The approximate s-type NOs, which are remarkably accurate at sufficiently small radial distances and exhibit universal scaling, differ qualitatively from the eigenfunctions of the core Hamiltonian even at the $\omega \rightarrow \infty$ limit of vanishing electron correlation.

The prediction that the product of the nth negative-valued natural amplitude and $n^{4}$ tends to a constant at the $n \rightarrow \infty$ limit implies the asymptotic $n^{-8}$ decay of the occupation numbers $\{\nu _{nl}(\omega ) \}$ of the NOs. In fact, the expression

$$ \nu _{nl}(\omega ) = \frac{16 \, |\Psi (\omega ;\vec {0},\vec {0})|^2}{\pi ^2 \, \omega ^4} \; [n+\Delta _{nl}(\omega )]^{-8}, $$

(45)

where $\{ \Delta _{nl}(\omega ) \}$ are small numbers weakly dependent on n, appears to be universal, i.e., to hold for arbitrary $\omega$ and l. Interestingly, naive summation of this expression over n yields collective occupancies that exhibit the same proportionality constant of $\frac{|\Psi (\omega ;\vec {0},\vec {0})|^2}{\omega ^4}$ as those that follow from the large-l asymptotics of Hill [34].