Abstract
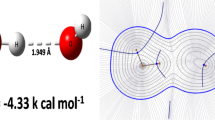
Ground-state energies for confined H2 molecule are computed using the variational method. The approach proposed here uses a molecular wave function of the valence bond type, written as the sum of the covalent term and the ionic term. The molecule is confined in an impenetrable prolate spheroidal box. The atomic orbitals are built from a previous suggestion inspired by the factorization of the Schrödinger equation. The aim of this work is to propose a new wave function to be used for the confined hydrogen molecule. The polarizability and quadrupole moment are also calculated. The results obtained are in agreement with other results present in the literature, and they lead to a discussion about the relevance of the ionic term in the wave function.


Similar content being viewed by others
References
Sabin JR, Brandas EJ (2009) Advances in quantum chemistry: theory of confined quantum systems-part one, vol 57. Academic Press, New York
Sabin JR, Brandas EJ (2009) Advances in quantum chemistry: theory of confined quantum systems-part two, vol 58. Academic Press, New York
Saha B, Mukherjee T, Mukherjee P et al (2002) Theor Chem Acc 108:305–310
Montgomery HE, Pupyshev VI (2015) Theor Chem Acc 134:1598
Mateos-Cortés S, Ley-Koo E, Cruz SA (2002) Int J Quantum Chem 86:376–389
LeSar R, Herschbach DR (1983) J Chem Phys 87:5202–5206
Connerade JP, Dolmatov VK, Lakshmi PA (2000) J Phys B At Mol Opt Phys 33:251–264
Lv H, Yao M, Li Q, Liu R, Liu B, Yao Z, Liu D, Liu Z, Liu J, Chen Z, Zou B, Cui T, Liu B (2015) Sci Rep 5:13234
Trzaskowsk B, Adamowicz L (2009) Theor Chem Acc 124:95–103
Cottrell TL (1951) Trans Faraday Soc 47:337–342
Singh KK (1964) Physica 30:211–222
Ley-Koo E, Cruz SA (1981) J Chem Phys 74:4603–4610
Sarsa A, Le Sech C (2012) J Phys B At Mol Opt Phys 45:205101
Micca Longo G, Longo S, Giordano D (2015) Phys Scr 90:025403
da Silva JF, Silva FR, Drigo Filho E (2016) Int J Quantum Chem 116:497–503
LeSar R, Herschbach DR (1981) J Phys Chem 85:2084–2798
Pang T (1994) Phys Rev A 49:1709–1713
Cruz SA, Soullard J, Gamaly E (1999) Phys Rev A 60:2207
Colín-Rodríguez R, Cruz SA (2010) J Phys B At Mol Opt Phys 43:235102
Powers A, Marsalek O, Xu M, Ulivi L, Colognesi D, Tuckerman ME, Bacic Z (2016) J Phys Chem Lett 7:308
Cruz SA, Soullard J (2004) J Chem Phys Lett 391:138–142
Jena NK, Tripathy MK, Samanta AK et al (2012) Theor Chem Acc 131:1205
Kozłoxwska J, Roztoczyńska A, Bartkowiak W (2015) Chem Phys 456:98–105
Silva FR (2014) Confinamento das moléculas H2 e O2 como modelo para o estudo da ligação ligante-sítio ativo em macromoléculas biológicas. Ph.D Thesis, São Jóse do Rio Preto, SP, Universidade Estadual Paulista (UNESP), Available from: Repositório Institucional UNESP. (in portuguese)
Levine IN (1991) Quantum chemistry. Prentice Hall, New York
Drigo Filho E, Ricotta RM (2002) Phys Lett A 299:137–143
Schiff LI (1968) Quantum mechanics. McGraw-Hill, New York
Silva FR, Drigo Filho E (2010) Mod Phys Lett A 25:641
Slater JC (1963) Quantum theory of molecules and solids: electronic structure of molecules. McGraw-Hill, New York
Kolos W, Roothaan CCJ (1960) Rev Mod Phys 32:219–232
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Batael, H.d., Drigo Filho, E. Ground-state energy for confined H2: a variational approach. Theor Chem Acc 137, 65 (2018). https://doi.org/10.1007/s00214-018-2243-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00214-018-2243-y