Abstract
We show by elementary means that every Kan fibration in simplicial sets can be embedded in a univalent Kan fibration.
Similar content being viewed by others
1 Introduction
A Kan fibration \(E \rightarrow U\) in the category of simplicial sets is universal in case every Kan fibration \(Y \rightarrow X\) satisfying certain size restrictions is a homotopy pullback of it. In this context, a typical such size restriction is to require \(Y \rightarrow X\) to have fibers of cardinality strictly less than a fixed regular cardinal. It was Voevodsky who first constructed such universal Kan fibrations and observed that the ones he constructed satisfied an additional property he dubbed univalence. Roughly, a Kan fibration \(E \rightarrow U\) in the category of simplicial sets is univalent if the path space of U is equivalent to the space of equivalences between fibers of \(E \rightarrow U\); see Sect. 4 below for a precise formulation. On the type-theoretic side this corresponds to a novel axiom (“the univalence axiom”), whose consequences are now being explored by many type theorists (see [12]). Following the work by Voevodsky, others have managed to construct, sometimes with considerable effort, fibrations which are both univalent and universal in other model categories (see, for example, [2, 4, 6, 7, 10, 11]).
In this paper we focus on the construction of univalent fibrations, whether universal or not. Indeed, we show that any fibration can be embedded, via a homotopy pullback, into a univalent one living in the same set-theoretic universe. The latter will then be universal whenever the former is. We give an elementary and detailed proof for the case of simplicial sets and explain in Remark 6 below how our methods can be extended to other model categories.
It should be pointed out that in the literature related to type theory, one also considers a stronger notion of universality, where every small fibration is isomorphic (rather than homotopy equivalent) to a pullback of the universal one. We will comment on the difference in Remark 2 below.
Although we were partially motivated by work on homotopy theoretic models of type theory, we wish to emphasize that our paper uses only basic definitions and results of the homotopy theory of simplicial sets, and is otherwise entirely self-contained.
2 Notation and background on groupoids
In this section we fix some notation and terminology concerning groupoids, actions by groupoids on other objects (i.e., representations), nerves, etc.
2.1 Actions
For a groupoid \(\mathbb {G}\), we write

for the sets of arrows and objects of \(\mathbb {G}\), and the source and target maps between them. Composition is denoted \(m: \mathrm{ar}(\mathbb {G}) \times _{\mathrm{ob}(\mathbb {G})} \mathrm{ar}(\mathbb {G}) \rightarrow \mathrm{ar}(\mathbb {G})\). A (left) action of \(\mathbb {G}\) on a set X consists of maps \(\pi : X \rightarrow \mathrm{ob}(\mathbb {G})\) and \(\alpha : \mathrm{ar}(\mathbb {G}) \times _{\mathrm{ob}(\mathbb {G})} X \rightarrow X\) satisfying the usual identities. We usually write \(g \cdot x\) for \(\alpha (g, x)\) where \(g: c \rightarrow d\) is an arrow in \(\mathbb {G}\) and x is an element of X with \(\pi (x) = c\). This action gives rise to a new groupoid denoted \(X_\mathbb {G}\), with \(\mathrm{ob}(X_\mathbb {G}) = X\) and \(\mathrm{ar}(X_\mathbb {G}) = \mathrm{ar}(\mathbb {G}) \times _{\mathrm{ob}(\mathbb {G})} X\). In fact, the arrows \(x \rightarrow y\) in \(X_\mathbb {G}\) are the arrows \(g: \pi x \rightarrow \pi y\) in \(\mathbb {G}\) with \(g \cdot x = y\). This groupoid is known as the action groupoid for the action of \(\mathbb {G}\) on X. It comes equipped with a functor (again) denoted \(\pi : X_\mathbb {G} \rightarrow \mathbb {G}\). Note that for each object c in \(\mathbb {G}\), there is a pullback of groupoids

where \(X_c = \pi ^{-1}(c) \subseteq X\) is viewed as a discrete groupoid (having identity arrows only).
2.2 Nerves
For a groupoid \(\mathbb {G}\), we write \(N(\mathbb {G})\) for its nerve. It is the simplicial set whose n-simplices are strings of composable arrows

in \(\mathbb {G}\). This definition of the nerve makes sense for any category, not just for groupoids. But for us, it will be convenient to observe that for a groupoid \(\mathbb {G}\), the data (1) can equivalently be represented in the form

where \(h_i: c_k \rightarrow c_i\) is the appropriate composition of \(g_i\)’s and their inverses. This representation has the advantage that all the faces \(d_i: N(\mathbb {G})_n \rightarrow N(\mathbb {G})_{n-1}\) other than \(d_k\) are simply given by deleting the arrow \(c_k \rightarrow c_i\). (This observation is related to the fact that \(N(\mathbb {G})\) is in fact a symmetric simplicial set, see, for instance, [5].)
If \(\mathbb {G}\) acts on X, then \(N(X_\mathbb {G})_n = X \times _{\mathrm{ob}(\mathbb {G})} N(\mathbb {G})_n\). This holds for both presentations (1) and (2). Thus, an n-simplex in \(N(X_\mathbb {G})\) can be represented as a pair
with \(\pi (x) = c_0\), similar to (1), or as a pair

with \(\pi (x) = c_k\), as in (2).
2.3 Simplicial groupoids
The definitions above make sense in any ambient category \(\mathcal {E}\) with pullbacks, giving rise to groupoid objects in \(\mathcal {E}\), actions on maps \(X \rightarrow \mathrm{ob}(\mathbb {G})\) in \(\mathcal {E}\), and simplicial objects \(N(\mathbb {G})\) and \(N(X_\mathbb {G})\) in \(\mathcal {E}\). If \(C^\bullet \) is a cosimplicial object in \(\mathcal {E}\) and \(\mathcal {E}\) has the necessary colimits, one can next take the “geometric realization”
to get back to \(\mathcal {E}\).
We will only be interested in the case where \(\mathcal {E}\) is the category \({s\mathcal {S}ets}\) of simplicial sets itself and \(C^\bullet \) is the cosimplicial object of standard simplices, \(C^n = \varDelta [n]\). In this case, \({\mathcal {E}}^{\mathbb {\varDelta }^{op}}\) is the category \({bis\mathcal {S}ets}\) of bisimplicial sets and the geometric realization is (isomorphic to) the diagonal, which we write as
It sends a bisimplicial set \(Y = \{ Y_{p, q} \}\) to its diagonal \(\delta ^*(Y)\) given by \(\delta ^*(Y)_n = Y_{n, n}\). We shall have occasion to use the left adjoint to \(\delta ^*\),
which is completely determined by its effect on representables,
If \(\mathbb {G}\) is a simplicial groupoid (a groupoid object in \({s\mathcal {S}ets}\)) its nerve is a bisimplicial set, and the diagonal thereof is denoted
and referred to as the classifying space of \(\mathbb {G}\) (using “space” as synonymous for simplicial set). In particular, if \(\mathbb {G}\) acts on a map \(\pi : X \rightarrow \mathrm{ob}(\mathbb {G})\) of simplicial sets, one obtains a map
of classifying spaces. Since both nerve and diagonal preserve pullbacks, one obtains for each object c in \(\mathbb {G}\) a pullback of simplicial sets

where \(1 = \varDelta [0]\) is the one-point simplicial set and \(X_c = \pi ^{-1}(c) \subseteq X\).
3 Fibration properties of simplicial groupoids
We will now list some conditions under which simplicial groupoids and their actions give rise to Kan complexes and Kan fibrations. These statements are all rather elementary and will be proved in detail.
Theorem 1
Let \(\mathbb {G}\) be a groupoid in \({s\mathcal {S}ets}\), and (for part (ii)) let \(\mathbb {G}\) act from the left on \(X \rightarrow \mathrm{ob}(\mathbb {G})\).
-
(i)
If \(\mathrm{ob}(\mathbb {G})\) is a Kan complex and \(s: \mathrm{ar}(\mathbb {G}) \rightarrow \mathrm{ob}(\mathbb {G})\) is a Kan fibration then \(B\mathbb {G}\) is a Kan complex.
-
(ii)
If \(\pi : X \rightarrow \mathrm{ob}(\mathbb {G})\) is a Kan fibration then so is \(B(X_\mathbb {G}) \rightarrow B\mathbb {G}\).
-
(iii)
If \(\mathbb {G}\) is transitive, i.e., if \((s, t): \mathrm{ar}(\mathbb {G}) \rightarrow \mathrm{ob}(\mathbb {G}) \times \mathrm{ob}(\mathbb {G})\) is surjective, then this map \((s, t): \mathrm{ar}(\mathbb {G}) \rightarrow \mathrm{ob}(\mathbb {G}) \times \mathrm{ob}(\mathbb {G})\) is a Kan fibration.
-
(iv)
If \((s, t): \mathrm{ar}(\mathbb {G}) \rightarrow \mathrm{ob}(\mathbb {G}) \times \mathrm{ob}(\mathbb {G})\) is a Kan fibration, then for any object c of \(\mathbb {G}\), i.e., any vertex c in \(\mathrm{ob}(\mathbb {G})\), there is a natural weak equivalence \(\mathbb {G}(c, c) \rightarrow \varOmega (B \mathbb {G}, c)\).
Remark 1
Part (iii) is what remains for groupoids of the classical fact that simplicial groups are Kan complexes [3, 8]. In part (iv), \(\varOmega (B \mathbb {G}, c)\) denotes the loop space of \(B \mathbb {G}\) at the base point c. It can be calculated inside simplicial sets as the evident subspace of \(B\mathbb {G}^{\varDelta [1]}\) in case \(B \mathbb {G}\) is Kan, cf. (i). Part (iv) is well known for simplicial groups, of course. As to the proofs, we will see that (i) and (ii) can be verified by direct inspection, while (iv) is an immediate consequence of (ii). The proof of (iii) is slightly more involved.
Proof of Theorem 1, part (i)
The case \(n = 1\) being trivial (since \(\varDelta [0] \subseteq \varDelta [1]\) is a retract), choose \(n \>1\) and \(0 \le k \le n\), and consider an extension problem of the form

By adjointness of \(\delta _!\) and \(\delta ^*\), this is equivalent to an extension problem of the form

in the category of bisimplicial sets. Also, by symmetry of the nerve of a groupoid [cf. (1) and (2) in Sect. 2 above] it suffices to consider the case \(k = 0\), and represent n-simplices in the nerve conveniently in the form

Thus, the data provided by \(\psi \) in (6) are matching faces which are diagrams in \(\mathbb {G}_{n-1}\) of the form

for all  , and the problem is to extend this to a diagram (7). (The notation in (8) is suggestive and should not lead to confusion: we are given these \(d_ic_j\) and \(d_ig_j\), but not the \(c_j\) and \(g_j\) themselves.) Since \(\mathrm{ob}(\mathbb {G})\) is assumed to be Kan, we can first extend the \(d_ic_0\),
, and the problem is to extend this to a diagram (7). (The notation in (8) is suggestive and should not lead to confusion: we are given these \(d_ic_j\) and \(d_ig_j\), but not the \(c_j\) and \(g_j\) themselves.) Since \(\mathrm{ob}(\mathbb {G})\) is assumed to be Kan, we can first extend the \(d_ic_0\),  , to an object \(c_0\) in \(\mathbb {G}_n\),
, to an object \(c_0\) in \(\mathbb {G}_n\),

where \(f = {\{d_ic_0\}_{i \>0}}\) is the map sending for each \(i \>0\) the face opposite the ith vertex to \(d_i c_0\). Next, for a fixed \(j \>0\), we are given \(d_ig_j :d_ic_0 \rightarrow d_ic_j\) for all \(i \not =0, j\). Let \(\varLambda ^{0, j}[n] \rightarrow \varDelta [n]\) be the union of all the faces except the ones opposite the 0th and jth vertex (i.e., the union of all the faces containing these two vertices). Then \(\varLambda ^{0, j}[n] \rightarrow \varDelta [n]\) is an anodyne extension. Since \(s: \mathrm{ar}(\mathbb {G}) \rightarrow \mathrm{ob}(\mathbb {G})\) is assumed to be a fibration, we can complete the diagram

where j is fixed and i ranges over all \(1, \ldots , { \hat{\jmath }}, \ldots , n\), to get a map \(g_j: \varDelta [n] \rightarrow \mathrm{ar}(\mathbb {G})\) as indicated. Doing this for each \(j \>0\) completes the family (8) into a diagram of the form (7). This proves part (i) of the theorem.
Proof of Theorem 1, part (ii)
We have to solve a lifting problem of the form

for each \(n \ge 0\) and each \(0 \le k \le n\). Again by symmetry, it suffices to prove this for \(k = 0\), and we can conveniently represent simplices in the nerves of the form (1) and (3) of Sect. 2. So the data provided by diagram (9) are an n-simplex  in \(N(\mathbb {G})_n\) and for each \(i \>0\) an element \(x_i \in X_{n-1}\) with \(\pi (x_i) = d_i c_0\), agreeing on overlapping faces. In particular, diagram (9) provides us with a commutative square
in \(N(\mathbb {G})_n\) and for each \(i \>0\) an element \(x_i \in X_{n-1}\) with \(\pi (x_i) = d_i c_0\), agreeing on overlapping faces. In particular, diagram (9) provides us with a commutative square

Since \(\pi \) is assumed to be a fibration, there exists a diagonal \(x: \varDelta [n] \rightarrow X\) in (10), which defines an n-simplex \((x, c_0 \rightarrow \cdots \rightarrow c_n)\) in \(N(X_\mathbb {G})\) and hence a diagonal in (9).
Before proving Part (iii), we observe the following elementary properties of Kan fibrations.
Lemma 1
(“Descent”) Consider a pullback diagram of simplicial sets

in which f is surjective. If \(p'\) is a Kan fibration, then so is p.
Proof
Immediate from the definitions.
Lemma 2
(“Quotients”) In a diagram

if \(g = f \circ p\) is a Kan fibration and p is a surjective Kan fibration, then f is a Kan fibration.
Proof
(See also [1, Proposition 4.1]) Consider a lifting problem as on the left

Let \(k: \varDelta [0] \rightarrow \varLambda ^k[n]\) be the k-th vertex. Then by assumption, \(b \circ k\) lifts to Z and we can next fill the square on the right. Since g is a Kan fibration and \(gc = ai\), there exists a map \(h: \varDelta [n] \rightarrow Z\) with \(gh = a\) and \(hi = c\). Then \(ph: \varDelta [n] \rightarrow Y\) is the required lift in the square on the left above.
Lemma 3
Let H be a simplicial group acting freely on a simplicial set E. Then \(E \rightarrow E/H\) is a Kan fibration.
Proof
Let us write \(X = E/H\) and \(q: E \rightarrow X\) for the quotient map. Then the lemma simply states that the principal H-bundle \(E \rightarrow X\) is a Kan fibration. This is well known, but here is an elementary proof. Consider the diagram

where \(\theta \) is the isomorphism \(\theta (h, e) = (h \cdot e, e)\). Since simplicial groups are Kan, \(H \rightarrow \varDelta [0]\) is a fibration, and hence so are its pullback \(H \times E \rightarrow E\) and the isomorphic map \(\pi _2: E \times _X E \rightarrow E\). By Lemma 1, \(q: E \rightarrow X\) is a Kan fibration.
Proof of Theorem 1, part iii)
Fix a vertex c in \(\mathrm{ob}(\mathbb {G})\), and write H for the simplicial group \(\mathbb {G}(c,c)\). Consider the pullback

So \(E = \mathbb {G}(-, c)\) is the simplicial set of arrows into c. The group H acts on E by composition, and this defines a principal H-bundle. Indeed, as for any groupoid, this action is free and transitive on the fibres of s. Moreover, these fibres are non-empty by the assumption that (s, t) is surjective. In particular, \(s: E \rightarrow \mathrm{ob}(\mathbb {G})\) is a Kan fibration by Lemma 3.
The group H also acts freely on the product \(E \times E\) by the diagonal action, so by the same lemma, \(E \times E \rightarrow (E \times E)/H\) is also a Kan fibration. But \((E \times E)/H\) is isomorphic to \(\mathrm{ar}(\mathbb {G})\) by an isomorphism that fits into

The diagonal is a Kan fibration by Lemma 2, and hence so is the map on the right.
Proof of Theorem 1, part (iv)
Again fix an object c in \(\mathbb {G}\), and now consider the pullback

So \(D = \mathbb {G}(c, -)\) is the simplicial set of arrows out of c. Then \(t: D \rightarrow \mathrm{ob}(\mathbb {G})\) is a Kan fibration since (s, t) is assumed to be. Composition of \(\mathbb {G}\) defines a left action by \(\mathbb {G}\) on D, so by Part (ii) of the theorem we obtain a Kan fibration \(B(D_\mathbb {G}) \rightarrow B(\mathbb {G})\) with fibre \(D_c = \mathbb {G}(c, c)\) [cf. the pullback square (5) in Sect. 2]. But \(D_\mathbb {G}\) is the simplicial groupoid \(c/\mathbb {G}\) which has an initial object. So \(B(D_\mathbb {G})\) is contractible, and the fibre of \(B(D_\mathbb {G}) \rightarrow B(\mathbb {G})\) is the loop space.
4 Universal Kan fibrations and univalence
Let us call a simplicial set small if it is countable, and a map small if it has countable fibres. (Countability is irrelevant here, in the sense that it could be replaced by any other bound by an infinite regular cardinal.)
Note that if \(f: Y \rightarrow X\) is small, then Quillen’s small object argument [3] gives a factorisation of f into an anodyne extension \(Y \rightarrow Y'\) and a small fibration \(Y' \rightarrow X\). More generally, any small f fits into a square

with horizontal anodyne extensions and a small fibration \(Y' \rightarrow X'\) into a Kan complex.
Definition 1
A small fibration \(\pi : E \rightarrow U\) is called universal if every small fibration \(Y \rightarrow X\) fits into a homotopy pullback

(That is, the map from Y to the pullback is a (weak) homotopy equivalence.)
Remark 2
As mentioned in the introduction, type theorists also consider a stronger notion of universality where every small fibration is isomorphic (rather than homotopy equivalent) to a pullback of the universal \(E \rightarrow U\). Let us call an \(E \rightarrow U\) with this property strictly universal. Obviously every strictly universal fibration is universal. But strictly universal maps are not very well behaved from the point of view of homotopy theory [(cf. Proposition 1. (iv) below]. Moreover, since weakly equivalent objects become isomorphic types in type theory, the weaker notion defined above suffices for most type-theoretic applications. This applies, for example, to the construction of models of CZF, or to the fact that univalence implies function extensionality.
We now state some elementary properties of universal fibrations. We omit the proofs, which are all obvious.
Proposition 1
-
(i)
If
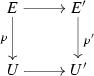
is a homotopy pullback where p and \(p'\) are small fibrations, then \(p'\) is universal whenever p is.
-
(ii)
In particular, any small universal fibration \(E \rightarrow U\) can be “completed” into another one \(E' \rightarrow U'\) with a Kan complex \(U'\) as base, as in
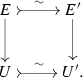
-
(iii)
In a homotopy pullback square as in (i), if
 is a weak equivalence and U is Kan then p is universal whenever \(p'\) is.
is a weak equivalence and U is Kan then p is universal whenever \(p'\) is. -
(iv)
In particular, as a property of small fibrations with a Kan complex as a base, being universal is invariant under (weak) homotopy equivalence.
Let \(E \rightarrow U\) be any fibration. We write \(\mathrm{End}(E) \rightarrow U \times U\) for the fibration constructed as the exponential \(\pi _2^*(E)^{\pi _1^*(E)} \rightarrow U \times U\) in \({s\mathcal {S}ets}/ U \times U\). Thus, the fibre over a pair (x, y) of vertices of U is \(E_y^{E_x} = \mathrm{Hom}(E_x, E_y)\). This fibration contains a subfibration \(\mathrm{Eq}(E) \rightarrow U \times U\) of weak equivalences between fibres. More explicitly, an n-simplex of \(\mathrm{Eq}(E)\) over \((x, y): \varDelta [n] \rightarrow U \times U \) is a weak equivalence \(x^* E \rightarrow y^* E\) over \(\varDelta [n]\). (The map \(\mathrm{Eq}(E) \rightarrow U \times U\) is again a fibration, since a map \(x^* E \rightarrow y^* E\) as above is a weak equivalence iff it is one over one or all vertices of \(\varDelta [n]\).)
Next, consider the “constant path” inclusion \(U \rightarrow U^{\varDelta [1]}\) and its pullback along \(U^{\varDelta [1]} \times _U E \rightarrow U^{\varDelta [1]}\). Both these maps are strong deformation retracts, hence trivial cofibrations, so the diagonal filling in the diagram below

gives a “connection” \(\nabla : U^{\varDelta [1]} \times _U E \rightarrow E\) over U, or \(U^{\varDelta [1]} \rightarrow \mathrm{End}(E)\) over \(U \times U\), which is easily seen to factor through \(\mathrm{Eq}(E) \subseteq \mathrm{End}(E)\). The fibration \(E \rightarrow U\) is said to be univalent [7] if this map \(U^{\varDelta [1]} \rightarrow \mathrm{Eq}(E)\) is a weak equivalence.
Remark 3
If \(x, y \in U\) are two vertices in the same component of U then \(\nabla \) provides a (zigzag of) weak equivalence(s) \(E_x \rightarrow E_y\). Suppose, conversely, that there is no weak equivalence \(E_x \rightarrow E_y\) if x and y belong to different components of U. Then by the long exact sequence of a fibration, univalence is equivalent to the statement that \(\nabla \) induces for each base point \(x_0 \in U\) a weak equivalence
where \(\varOmega (U, x_0)\) is the loop space of U at \(x_0\) (constructed as the homotopy fibre of \(U^{\varDelta [1]} \rightarrow U \times U\), or simply as the fibre if U is Kan) and \(\mathrm{Eq}(E_{x_0})\) is the simplicial set of self-equivalences of \(E_{x_0}\). Indeed, in order to compare the (homotopy) fibres of

we can restrict ourselves to diagonal base points, because the (homotopy) fibre of either map over (x, y) is non-empty iff x and y belong to the same connected component.
Remark 4
Univalence is invariant under (weak) homotopy equivalence, in the sense that if

is a weak equivalence between two fibrations p and \(p'\), then p is univalent iff \(p'\) is. Vice versa, if \(E \rightarrow U\) and \(E' \rightarrow U'\) are two univalent universal fibrations then they fit into such a square. In this sense, “the” universal univalent fibration is unique up to homotopy.
5 Univalent completion
In this section, we will show that any fibration can be embedded into a univalent one, in the following sense.
Theorem 2
Let \(E \rightarrow U\) be a fibration. Then there exists a homotopy pullback square

where \(p'\) is univalent and \(U \rightarrow U'\) is mono. Moreover, if p is small then so is \(p'\), and if p is universal then so is \(p'\).
Remark 5
It will be obvious from the construction that \(p'\) is small whenever p is. Moreover, universality of \(p'\) follows from that of p by Proposition 1. Note that, in contrast, any universal fibration \(E \rightarrow U\) can be trivially embedded into a universal fibration which is not univalent, such as \(E + Y \rightarrow U + X\) where \(Y \rightarrow X\) is an arbitrary fibration satisfying the size restrictions.
Proof of Theorem 2
Fix \(p: E \rightarrow U\), and choose a minimal fibration inside E [3, 8]:

Thus, M is a fibrewise deformation retract of E. Moreover, by minimality, any weak equivalence \(M_x \rightarrow M_y\) between fibres of M is an isomorphism. Thus, we obtain maps

and \(M \rightarrow U\) is homotopy equivalent to \(E \rightarrow U\) hence universal whenever \(E \rightarrow U\) is. Thus, to prove the theorem, we might as well assume that \(E \rightarrow U\) is a minimal fibration, as we will now do.
Let \(\mathbb {G}\) be the simplicial groupoid with \(\mathrm{ob}(\mathbb {G}) = U\) and \(\mathrm{ar}(\mathbb {G}) = \mathrm{Iso}(E)\). In other words, an n-simplex in \(\mathrm{ar}(\mathbb {G})\) is a triple \((x, y, \alpha )\) where \(x, y: \varDelta [n] \rightarrow U\) and \(\alpha : x^* E \rightarrow y^* E\) is an isomorphism over \(\varDelta [n]\). Then \(\mathbb {G}\) acts on \(E \rightarrow U\) in the obvious way, so we obtain a pullback square of simplicial sets

The map \(p'\) on the right is a Kan fibration by Theorem 1.(ii). Moreover, since \(\mathrm{ar}(\mathbb {G}) \rightarrow \mathrm{ob}(\mathbb {G}) \times \mathrm{ob}(\mathbb {G})\) is the Kan fibration \(\mathrm{Iso}(E) = \mathrm{Eq}(E) \rightarrow U \times U\), it follows from Theorem 1.(iv) that there is a weak equivalence \(\mathbb {G}(x_0, x_0) \rightarrow \varOmega (B\mathbb {G}, x_0)\) for any vertex \(x_0\) in U. But \(\mathbb {G}(x_0, x_0) = \mathrm{Iso}(E_{x_0}) = \mathrm{Eq}(E_{x_0})\), so this proves that \(p'\) is univalent provided the condition on connected components is satisfied (cf. Remark 3 above). We conclude the proof by checking this condition: The map \(i: U \rightarrow B\mathbb {G}\) is an isomorphism on vertices, and the fibre of \(p'\) over a vertex i(x) is \(E_x\). If x and y are in the same connected component of \(B\mathbb {G}\) then they are related by a weak equivalence provided by a “connection” \(\nabla \) for \(p'\). And conversely, if \(E_x\) and \(E_y\) are related by a weak equivalence, then by construction there is an arrow in \(\mathbb {G}\) from x to y, hence x and y are in the same connected component of \(B\mathbb {G}\). This completes the proof.
Remark 6
It is perhaps of interest to remark that it is possible to avoid the use of minimal fibrations in the proof of Theorem 2. Instead, one can use the following version of the “group completion theorem” from [9], concerning a category object \(\mathbb {C}\) in \({s\mathcal {S}ets}\) (rather than a groupoid object \(\mathbb {G}\) considered before) and an action by \(\mathbb {C}\) on a Kan fibration \(X \rightarrow \mathrm{Ob}(\mathbb {C})\).
Theorem 3
If \(\mathbb {C}\) acts on X by weak equivalences, then each pullback square

is a homotopy pullback.
This is stated in [9, Theorem 2.1] for a category object \(\mathbb {C}\) with \(\mathrm{ob}(\mathbb {C})\) discrete, but this plays no rôle in the proof given there. To say that \(\mathbb {C}\) acts by weak equivalences simply means that for each arrow \(\alpha : c \rightarrow d\) in \(\mathbb {C}_0\), the induced map \(X_c \rightarrow X_d\) is a weak equivalence. Theorem 2 can now be proved by applying Theorem 3 to the category \(\mathbb {C}\) defined by \(\mathrm{ob}(\mathbb {C}) = U\) and \(\mathrm{ar}(\mathbb {C}) = \mathrm{Eq}(E)\), the space of equivalences between fibres of \(E \rightarrow U\).
This line of proof also applies to versions of Theorem 2 in model categories such as categories of simplicial presheaves.
References
van den Berg, B., Moerdijk, I.: W-types in homotopy type theory. Math. Struct. Comput. Sci. 25(5), 1100–1115 (2015)
Cisinski, D.-C.: Univalent universes for elegant models of homotopy types (2014). arXiv:1406.0058
Gabriel, P., Zisman, M.: Calculus of Fractions and Homotopy Theory. Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 35. Springer-Verlag New York, Inc., New York (1967)
Gepner, D., Kock, J.: Univalence in locally cartesian closed \(\infty \)-categories. Forum Math. 29(3), 617–652 (2017)
Grandis, M.: Finite sets and symmetric simplicial sets. Theory Appl. Categ. 8, 244–252 (2001)
Hofmann, M., Streicher, T.: The groupoid interpretation of type theory. Twenty-Five Years of Constructive Type Theory (Venice, 1995). Oxford Logic Guides, vol. 36, pp. 83–111. Oxford University Press, New York (1998)
Kapulkin, K., Lumsdaine, P.L.: The simplicial model of univalent foundations (after Voevodsky) (2016). arXiv:1211.2851
May, J.P.: Simplicial Objects in Algebraic Topology. Van Nostrand Mathematical Studies, vol. 11. D. Van Nostrand Co., Inc., Princeton (1967)
Moerdijk, I.: Bisimplicial sets and the group-completion theorem. Algebraic \(K\)-Theory: Connections with Geometry and Topology (Lake Louise, AB, 1987). NATO Adv. Sci. Inst. Ser. C. Math. Phys. Sci., vol. 279, pp. 225–240. Kluwer Academic Publishers, Dordrecht (1989)
Shulman, M.: The univalence axiom for elegant Reedy presheaves. Homol. Homotopy Appl. 17(2), 81–106 (2015)
Shulman, M.: Univalence for inverse diagrams and homotopy canonicity. Math. Struct. Comput. Sci. 25(5), 1203–1277 (2015)
The Univalent Foundations Program. Homotopy type theory—univalent foundations of mathematics. The Univalent Foundations Program, Princeton, NJ. Institute for Advanced Study (IAS), Princeton (2013)
Acknowledgements
We are grateful to the referees for their careful reading of an earlier version of this paper. The results of this paper were presented by the second named author at workshops in Sheffield and at the Mittag-Leffler Institute in Stockholm in March and June 2015, respectively. We are especially grateful to the Institute: it was there that this paper acquired its present form.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Thomas Schick.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.



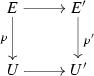

 is a weak equivalence and U is Kan then p is universal whenever
is a weak equivalence and U is Kan then p is universal whenever