Global Lipschitz continuity for minima of degenerate problems

Abstract

We consider the problem of minimizing the Lagrangian $\int [F(\nabla u)+f\,u]$ among functions on $\Omega \subset \mathbb {R}^N$ with given boundary datum $\varphi$. We prove Lipschitz regularity up to the boundary for solutions of this problem, provided $\Omega$ is convex and $\varphi$ satisfies the bounded slope condition. The convex function F is required to satisfy a qualified form of uniform convexity only outside a ball and no growth assumptions are made.

Appendix: Uniformly convex functions outside a ball

1.1 Basic properties

We first present a characterization of uniformly convex functions outside a ball in terms of second order derivatives.

Lemma 7.1

Let $F:\mathbb {R}^N\rightarrow \mathbb {R}$ be a convex function and $\{\rho _{\varepsilon }\}_{\varepsilon >0}\subset C^{\infty }_0(B_{\varepsilon })$ be a sequence of standard mollifiers.

• (i) Assume that F is $\Phi$-uniformly convex outside some ball $B_R$. Then for every $\varepsilon >0$, for every $R'>R+\varepsilon$, for every $\xi \in B_{R'}{\setminus } B_{R+\varepsilon }$ and $\eta \in \mathbb {R}^N$,

  $$\begin{aligned} \langle D^2 (F*\rho _{\varepsilon })(\xi )\,\eta , \eta \rangle \ge \left( \min _{t\in [2\,R,2\,(R'+\varepsilon )]}\Phi (t)\right) \, |\eta |^2. \end{aligned}$$

  (7.1)

• (ii) Assume that there exist $\mu >0$ and $R>0$ such that for every $\varepsilon >0$, for every $|x|\ge R+\varepsilon$, for every $\eta \in \mathbb {R}^N$,

  $$\begin{aligned} \langle D^2 (F*\rho _{\varepsilon })(x)\,\eta , \eta \rangle \ge \mu \, |\eta |^2. \end{aligned}$$

  (7.2)

  Then F is $\mu$-uniformly convex outside $B_R$.

Proof

Assume first that F is $\Phi$-uniformly convex outside $B_R$. For every $\xi \in B_{R'}{\setminus } B_{R+\varepsilon }$, for every $y\in B_{\varepsilon }, \eta \in \mathbb {R}^N$ and every $h>0$ sufficiently small, the segment $[\xi +h\,\eta -y, \xi -h\,\eta -y]$ does not intersect $B_R$. Hence

$$\begin{aligned} F(\xi -y)\le & {} \frac{1}{2}F(\xi +h\,\eta -y) + \frac{1}{2}F(\xi -h\,\eta -y)\\&-\frac{1}{2}\,h^2\,|\eta |^2\,\Phi (|\xi +h\,\eta -y|+|\xi -h\,\eta -y|)\\\le & {} \frac{1}{2}F(\xi +h\,\eta -y) + \frac{1}{2}F(\xi -h\,\eta -y)\\&-\frac{1}{2}\, h^2\,|\eta |^2 \left( \min _{t\in [2\,R, 2\,(R'+\varepsilon + h\,|\eta |)]}\Phi (t)\right) . \end{aligned}$$

By multiplying by $\rho _\varepsilon (y)$ and integrating, this gives

$$\begin{aligned}&F*\rho _{\varepsilon }(\xi )\le \frac{1}{2}F*\rho _{\varepsilon }(\xi +h\,\eta ) + \frac{1}{2}F*\rho _{\varepsilon }(\xi -h\,\eta ) \\&-\frac{1}{2}\,h^2\,|\eta |^2\,\left( \min _{t\in [2\,R, 2\,(R'+\varepsilon + h\,|\eta |)]}\Phi (t)\right) . \end{aligned}$$

Hence, we get

$$\begin{aligned} \langle D^2 (F*\rho _{\varepsilon })(\xi )\,\eta , \eta \rangle= & {} \lim _{h\rightarrow 0}\frac{F*\rho _{\varepsilon }(\xi +h\,\eta ) + F*\rho _{\varepsilon }(\xi -h\,\eta )-2\,F*\rho _{\varepsilon }(\xi )}{h^2}\\\ge & {} \left( \min _{t\in [2\,R, 2\,(R'+\varepsilon )]}\Phi (t)\right) \,|\eta |^2. \end{aligned}$$

This completes the proof of (7.1).

Assume now that (7.2) holds true. Let $\theta \in [0,1]$ and $\xi , \xi '\in \mathbb {R}^N$ be such that $[\xi ,\xi ']\cap B_{R} = \emptyset$. For every $\varepsilon >0$, we take $\xi _\varepsilon ,\xi _\varepsilon '\in \mathbb {R}^N$ such that $[\xi _\varepsilon ,\xi '_\varepsilon ]\cap B_{R+\varepsilon } = \emptyset$ and

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0} |\xi _\varepsilon -\xi |=0\quad \text{ and } \quad \lim _{\varepsilon \rightarrow 0} |\xi '_\varepsilon -\xi '|=0. \end{aligned}$$

We have

$$\begin{aligned} F*\rho _{\varepsilon }(\xi _\varepsilon )= & {} F*\rho _{\varepsilon }(\theta \,\xi _\varepsilon +(1-\theta )\,\xi '_\varepsilon )\\&+(1-\theta )\,\langle \nabla (F*\rho _{\varepsilon })(\theta \,\xi _\varepsilon +(1-\theta )\,\xi '_\varepsilon ), \xi _\varepsilon -\xi '_\varepsilon \rangle \\&+(1-\theta )^2\,\int _{0}^1(1-t)\,\langle D^2 (F*\rho _{\varepsilon })(t\,\xi _\varepsilon +(1-t)\,(\theta \,\xi _\varepsilon +(1-\theta )\,\xi '_\varepsilon ))\\&\times (\xi _\varepsilon -\xi '_\varepsilon ),\xi _\varepsilon -\xi '_\varepsilon \rangle \,dt. \end{aligned}$$

Since the segment $[\xi _\varepsilon , \theta \,\xi _\varepsilon +(1-\theta )\,\xi '_\varepsilon ]$ does not intersect $B_{R+\varepsilon }$, assumption (7.2) implies

$$\begin{aligned} F*\rho _{\varepsilon }(\xi _\varepsilon )\ge & {} F*\rho _{\varepsilon }(\theta \,\xi _\varepsilon +(1-\theta )\,\xi '_\varepsilon )\\&+(1-\theta )\,\langle \nabla (F*\rho _{\varepsilon })(\theta \,\xi _\varepsilon +(1-\theta )\,\xi '_\varepsilon ), \xi _\varepsilon -\xi '_\varepsilon \rangle \\&+ \frac{\mu }{2}\, (1-\theta )^2\,|\xi _\varepsilon -\xi '_\varepsilon |^2. \end{aligned}$$

Similarly, we get

$$\begin{aligned} F*\rho _{\varepsilon }(\xi _\varepsilon ')\ge & {} F*\rho _{\varepsilon }(\theta \,\xi _\varepsilon +(1-\theta )\,\xi '_\varepsilon )+\theta \,\langle \nabla (F*\rho _{\varepsilon })(\theta \,\xi _\varepsilon +(1-\theta )\,\xi '_\varepsilon ), \xi '_\varepsilon -\xi _\varepsilon \rangle \\&+ \frac{\mu }{2}\, \theta ^2\,|\xi _\varepsilon -\xi '_\varepsilon |^2. \end{aligned}$$

We multiply the first inequality by $\theta$ and the second one by $(1-\theta )$. By summing them, we get

$$\begin{aligned}&\theta \, F*\rho _{\varepsilon }(\xi _\varepsilon ) + (1-\theta )\,F*\rho _{\varepsilon }(\xi '_\varepsilon )\\&\quad \ge F*\rho _{\varepsilon }(\theta \,\xi _\varepsilon +(1-\theta )\,\xi '_\varepsilon ) +\frac{\mu }{2}\,\theta \,(1-\theta )\,|\xi _\varepsilon - \xi '_\varepsilon |^2. \end{aligned}$$

We then let $\varepsilon$ go to 0 to obtain (1.5). This completes the proof. $\square$

We will also need the following technical result. Here $\mathcal {H}^1$ denotes the 1-dimensional Hausdorff measure.

Lemma 7.2

Let F be a convex function which is $\mu$-uniformly convex outside $B_R\subset \mathbb {R}^N$. For every $\xi , \xi ' \in \mathbb {R}^N$ and every $\zeta \in \partial F(\xi )$, we have

$$\begin{aligned} F(\xi ')\ge F(\xi ) + \langle \zeta , \xi '-\xi \rangle + \frac{\mu }{4}\, \mathcal {H}^1([\xi , \xi ']{\setminus } B_R)^2. \end{aligned}$$

(7.3)

Proof

We can assume that $\xi \not =\xi '$. We have several possible cases:

Fig. 2

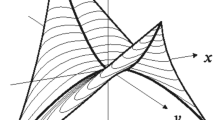
The two possibilities for Case C in the proof of Lemma 7.2

• Case A $\mathcal {H}^1([\xi ,\xi ']{\setminus } B_R)=\mathcal {H}^1([\xi ,\xi '])$. In this case, the segment $[\xi ,\xi ']$ does not intersect $B_R$ and thus (7.3) follows directly from (3.1) with $\Phi \equiv \mu$.

• Case B $\mathcal {H}^1([\xi ,\xi ']{\setminus } B_R)=0$. Then (7.3) follows from the convexity of F.

• Case C $0<\mathcal {H}^1([\xi ,\xi ']{\setminus } B_R)<\mathcal {H}^1([\xi ,\xi '])$. Without loss of generality, we may assume that $\xi \not \in \overline{B_R}$ and that the half-line $\{\xi +t(\xi '-\xi ) ; t\ge 0\}$ intersects the sphere $\partial B_R$ at two points $\xi _1, \xi _2$ such that $\xi _1\in [\xi _2, \xi ]$. We now in turn have to consider two cases:

  $$\begin{aligned} \xi ' \in [\xi _1, \xi _2]\quad \text{ or }\quad \xi _2\in [\xi ', \xi _1], \end{aligned}$$

  (see Fig. 2 above). When $\xi ' \in [\xi _1, \xi _2]$, we use the fact that the segment $[\xi _1, \xi ]$ lies outside the ball $B_R$. It follows from (3.1) with $\Phi \equiv \mu$ that for every $\zeta _1\in \partial F(\xi _1)$,

  $$\begin{aligned} F(\xi )\ge F(\xi _1)+\langle \zeta _1, \xi -\xi _1\rangle +\frac{\mu }{2}\,|\xi -\xi _1|^2. \end{aligned}$$

  (7.4)

  Let $\zeta '\in \partial F(\xi ')$. By convexity of F, we also have

  $$\begin{aligned} F(\xi _1)\ge F(\xi ')+\langle \zeta ', \xi _1-\xi '\rangle , \end{aligned}$$

  (7.5)

  and

  $$\begin{aligned} \langle \zeta _1-\zeta ', \xi _1-\xi '\rangle \ge 0, \end{aligned}$$

  since the subdifferential of F is a monotone map. The latter inequality implies that

  $$\begin{aligned} \langle \zeta _1-\zeta ', \xi -\xi _1\rangle \ge 0. \end{aligned}$$

  Together with (7.4) and (7.5), with some manipulations this yields

  $$\begin{aligned} F(\xi )\ge & {} F(\xi ') +\langle \zeta ', \xi -\xi '\rangle +\frac{\mu }{2}\,|\xi -\xi _1|^2\\= & {} F(\xi ')+\langle \zeta ', \xi -\xi ' \rangle +\frac{\mu }{2}\,\mathcal {H}^1([\xi ,\xi ']{\setminus } B_R)^2, \end{aligned}$$

  which settles the first case. In the second case, in addition to (7.4), we also use the fact that for every $\zeta _2 \in \partial F(\xi _2)$,

  $$\begin{aligned} F(\xi _1)\ge F(\xi _2) +\langle \zeta _2, \xi _1-\xi _2\rangle , \end{aligned}$$

  and for every $\zeta '\in \partial F(\xi ')$

  $$\begin{aligned} F(\xi _2) \ge F(\xi ') + \langle \zeta ', \xi _2- \xi '\rangle +\frac{\mu }{2}\,|\xi _2-\xi '|^2, \end{aligned}$$

  again by (3.1) with $\Phi \equiv \mu$. By using as in the first case that $\langle \zeta _1-\zeta ', \xi -\xi _1\rangle \ge 0$ and $\langle \zeta _2-\zeta ', \xi _1-\xi _2\rangle \ge 0$, we thus obtain

  $$\begin{aligned} F(\xi )\ge & {} F(\xi ') +\langle \zeta ', \xi -\xi '\rangle +\frac{\mu }{2}\,(|\xi -\xi _1|^2+|\xi '-\xi _2|^2)\\\ge & {} F(\xi ') +\langle \zeta ', \xi -\xi '\rangle +\frac{\mu }{4}\,\mathcal {H}^1([\xi , \xi ']{\setminus } B_R)^2. \end{aligned}$$

This completes the proof of (7.3). $\square$

Thanks to the previous result, we can detail some consequences of the uniform convexity that we used in the proof of the Main Theorem.

Lemma 7.3

Let F be a convex function which is $\mu$-uniformly convex outside $B_R\subset \mathbb {R}^N$. Then we have:

• (i) for every $\xi , \xi '\in \mathbb {R}^N$, and every $\zeta \in \partial F(\xi )$, if $|\xi |\ge 2R$ or $|\xi '|\ge 2R$, then there holds

  $$\begin{aligned} F(\xi ')\ge F(\xi ) +\langle \zeta , \xi '-\xi \rangle +\frac{\mu }{36}\,|\xi '-\xi |^2; \end{aligned}$$

  (7.6)

• (ii) for every $\xi , \xi '\in \mathbb {R}^N$, and every $\zeta \in \partial F(\xi ), \zeta '\in \partial F(\xi ')$, if $|\xi |\ge 2R$ or $|\xi '|\ge 2R$ we have

  $$\begin{aligned} \langle \zeta -\zeta ', \xi -\xi '\rangle \ge \frac{\mu }{18}\,|\xi -\xi '|^2; \end{aligned}$$

  (7.7)

• (iii) for every $\xi , \xi '\in \mathbb {R}^N{\setminus } B_{2\,R}$ and for every $\theta \in [0,1]$,

  $$\begin{aligned} F(\theta \, \xi + (1-\theta )\,\xi ')\le \theta \, F(\xi ) + (1-\theta )\,F(\xi ') -\frac{\mu }{36}\,\theta \,(1-\theta )\, |\xi -\xi '|^2;\nonumber \\ \end{aligned}$$

  (7.8)

• (iv) for every $\xi \in \mathbb {R}^N$, if $|\xi |\ge 2R$, then

  $$\begin{aligned} F(\xi )\ge \frac{\mu }{72}\,|\xi |^2 -\left( |F(0)|+\frac{18}{\mu }\,|\partial ^o F(0)|^2\right) , \end{aligned}$$

  (7.9)

  where $\partial ^o F(0)$ denotes the element of $\partial F(0)$ having minimal Euclidean norm.

Proof

We claim that for every $\xi \in \mathbb {R}^N$ and every $\xi '\in \mathbb {R}^N{\setminus } B_{2\,R}$,

$$\begin{aligned} \mathcal {H}^1([\xi , \xi ']{\setminus } B_R) \ge \frac{1}{3}\, |\xi -\xi '|. \end{aligned}$$

(7.10)

Let us fix $\xi '\in \mathbb {R}^N{\setminus } B_{2\,R}$ and let $\xi \in \mathbb {R}^N$. We set $r=|\xi '-\xi |>0$. Then we see that among all $\xi$ such that $|\xi -\xi '|=r$, the length of the set $[\xi , \xi ']{\setminus } B_R$ is minimal for the vector

$$\begin{aligned} \xi '':=t\,\xi ',\quad \text{ with } t<1 \text{ such } \text{ that } (1-t)=\frac{r}{|\xi '|}. \end{aligned}$$

Then we have

$$\begin{aligned} \mathcal {H}^1([\xi ',\xi '']{\setminus } B_R)=\left\{ \begin{array}{ll} r,&{}\quad \text{ if } r\le |\xi '|-R,\\ |\xi '|-R&{}\quad \text{ if } |\xi '|-R<r<|\xi '|+R,\\ r-2\,R, &{}\quad \text{ if } |\xi '|+R\le r. \end{array} \right. \end{aligned}$$

Observe that

$$\begin{aligned} \frac{|\xi '|}{2}\le |\xi '|-R, \end{aligned}$$

thus for $|\xi '|-R<r<|\xi '|+R$ we have

$$\begin{aligned} r<3\,\frac{|\xi '|}{2}\le 3\,(|\xi '|-R)=3\,\mathcal {H}^1([\xi ',\xi '']{\setminus } B_R). \end{aligned}$$

Similarly, for $|\xi '|+R\le r$, we have

$$\begin{aligned} \mathcal {H}^1([\xi ',\xi '']{\setminus } B_R)=r-2\,R=\frac{r}{3}+\left( \frac{2}{3}\,r-2\,R\right) \ge \frac{r}{3}+\left( \frac{2}{3}\,|\xi '|-\frac{4}{3}\,R\right) \ge \frac{r}{3}. \end{aligned}$$

By recalling that $r=|\xi -\xi '|$, the claim (7.10) follows. The inequality (7.6) can now be easily deduced from (7.3) and (7.10).

Inequality (7.7) can be easily obtained from (7.6). Indeed, by exchanging the role of $\xi$ and $\xi '$ in (7.6) we get

$$\begin{aligned} F(\xi ')-F(\xi )\ge \langle \zeta ,\xi '-\xi \rangle +\frac{\mu }{36}\, |\xi -\xi '|^2, \end{aligned}$$

and

$$\begin{aligned} F(\xi )-F(\xi ')\ge \langle \zeta ',\xi -\xi '\rangle +\frac{\mu }{36}\, |\xi -\xi '|^2. \end{aligned}$$

By combining these two inequalities we get (7.7).

Let us take $\xi , \xi '\in \mathbb {R}^N{\setminus } B_{2R}$. For every $\theta \in [0,1]$ and every $\zeta \in \partial F(\theta \, \xi +(1-\theta )\,\xi ')$ by (7.6) we get

$$\begin{aligned} F(\xi )\ge F(\theta \,\xi + (1-\theta )\,\xi ') +(1-\theta )\,\langle \zeta , \xi -\xi '\rangle +\frac{\mu }{36}\,(1-\theta )^2|\xi '-\xi |^2, \end{aligned}$$

and

$$\begin{aligned} F(\xi ')\ge F(\theta \,\xi + (1-\theta )\,\xi ') +\theta \, \langle \zeta , \xi '-\xi \rangle +\frac{\mu }{36}\, \theta ^2\,|\xi '-\xi |^2. \end{aligned}$$

Then (7.8) can be obtained by multipliying the first inequality by $\theta$, the second one by $(1-\theta )$ and then summing up.

Finally, we use (7.6) with $\xi '\in \mathbb {R}^N{\setminus } B_{2R}$, $\xi =0$ and $\zeta =\partial ^o F(0)$ as in the statement, then we obtain

$$\begin{aligned} F(\xi ') \ge F(0) + \langle \zeta , \xi '\rangle + \dfrac{\mu }{36}\,|\xi '|^2&\ge \dfrac{\mu }{72}\, |\xi '|^2-\left( |F(0)|+\dfrac{18}{\mu }\,\,|\zeta |^2\right) , \end{aligned}$$

where we used Young inequality in the last passage. This proves (7.9).

1.2 Approximation issues

This section is devoted to prove some approximation results we used in the proof of the Main Theorem.

Lemma 7.4

Let $F:\mathbb {R}^N\rightarrow \mathbb {R}$ be a convex function, which is $\mu$-uniformly convex outside the ball $B_R$ for some $\mu >0$ and $R>0$. Then there exists a nondecreasing sequence $\{F_k\}_{k\in \mathbb {N}}$ of smooth convex functions which converges to F uniformly on bounded sets. Moreover, $F_k$ is $(\mu /36)$-uniformly convex outside $B_{R+1}$.

Proof

Let us set for simplicity $\mu '=\mu /36$. For every $k\in \mathbb {N}$, we define at first

$$\begin{aligned} \widetilde{F}_k(x):=\sup _{\begin{array}{c} |y|\le k\\ \zeta \in \partial F(y) \end{array}} \left[ F(y)+\langle \zeta , x-y\rangle + \frac{\mu '}{2}\,|x-y|^2\, 1_{\mathbb {R}^N{\setminus } B_{2\,R}}(y)\right] ,\quad x\in \mathbb {R}^N. \end{aligned}$$

Of course, this is a nondecreasing sequence of convex functions. If $k\le 2\,R$, then by convexity of F for every $|y|\le k$, every $\zeta \in \partial F(y)$ and every $x\in \mathbb {R}^N$ we get

$$\begin{aligned} F(y)+\langle \zeta , x-y\rangle + \frac{\mu '}{2}\,|x-y|^2\, 1_{\mathbb {R}^N{\setminus } B_{2\,R}}(y)\le F(x). \end{aligned}$$

(7.11)

If $k>2\, R$ and $|y|\le k$, we have two possibilities: either $|y|\le 2\,R$ or $|y|>2\,R$. In the first case we still have (7.11) for every $\zeta \in \partial F(y)$ and $x\in \mathbb {R}^N$, simply by convexity of F. In the second case, we can appeal to inequality (7.6) of Lemma 7.3: indeed, for every $x \in \mathbb {R}^N$ and every $\zeta \in \partial F(y)$, we have

$$\begin{aligned} F(x)\ge F(y)+\langle \zeta , x-y\rangle + \mu '\,|x-y|^2. \end{aligned}$$

In any case, we obtain that for every $x\in \mathbb {R}^N$

$$\begin{aligned} \widetilde{F}_k(x)\le F(x), \end{aligned}$$

and the equality holds when $x\in \overline{B_k}$. In particular, for every $k\ge R$ the function $\widetilde{F}_k$ is $\mu$-uniformly convex on $\overline{B_k} {\setminus } B_R$.

When $k\ge 2\,R+1$ and $|x|\ge 2\,R$, we claim that

$$\begin{aligned} \widetilde{F}_k(x)=\sup _{\begin{array}{c} 2\,R\le |y|\le k\\ \zeta \in \partial F(y) \end{array}} \left[ F(y)+\langle \zeta , x-y\rangle + \frac{\mu '}{2}\,|x-y|^2\right] . \end{aligned}$$

(7.12)

This follows from the fact that for every $y_0 \in B_{2R}$ and $\zeta _0\in \partial F(y_0)$, there exists $y\in \overline{B_{k}}{\setminus } B_{2R}$ and $\zeta \in \partial F(y)$ such that

$$\begin{aligned} F(y)+\langle \zeta , x-y\rangle \ge F(y_0)+\langle \zeta _0, x-y_0\rangle . \end{aligned}$$

(7.13)

Indeed, take any $y\in [y_0,x]\cap (\overline{B_k}{\setminus } B_{2R})$ and any $\zeta \in \partial F(y)$. Then, by convexity of F,

$$\begin{aligned} F(y)\ge F(y_0) + \langle \zeta _0, y-y_0\rangle . \end{aligned}$$

Hence, by using this and the fact that $y-x=t\,(y_0-y)$ for some $t\ge 0$, we can infer

$$\begin{aligned} F(y)+\langle \zeta , x-y\rangle\ge & {} F(y_0)+\langle \zeta _0, y-y_0\rangle +\langle \zeta , x-y\rangle \\= & {} F(y_0)+\langle \zeta _0, x-y_0\rangle +\langle \zeta _0-\zeta , y-x\rangle \\= & {} F(y_0)+\langle \zeta _0, x-y_0\rangle +t\,\langle \zeta _0-\zeta , y_0-y\rangle \\\ge & {} F(y_0)+\langle \zeta _0, x-y_0\rangle . \end{aligned}$$

In the last line, we have used the monotonicity of the subdifferential. This proves (7.13) and thus (7.12).

It follows that $\widetilde{F}_k$ is $\mu '$-uniformly convex on $\mathbb {R}^N{\setminus } B_{2\,R}$ as the supremum of $\mu '$-uniformly convex functions on $\mathbb {R}^N{\setminus } B_{2\,R}$. Since $\mu '<\mu$, on the whole we get that $\widetilde{F}_k$ is $\mu '$-uniformly convex on $\mathbb {R}^N{\setminus } B_R$.

In the remaining part of the proof, we fix some $k\ge 2\,R+1$. We claim that for every $x\in \mathbb {R}^N$,

$$\begin{aligned} \widetilde{F}_{k+1}(x)\ge \widetilde{F}_{k}(x) + \mu '\,(|x|-k-1)_+. \end{aligned}$$

(7.14)

If $|x|\le k+1$ this is immediate (recall that $\widetilde{F}_k$ is nondecreasing), thus let us assume that $|x|>k+1$. Let $y_0\in \overline{B_k}{\setminus } B_{2\,R}$ and $\zeta _0\in \partial F(y_0)$ achieving the supremum in the definition of $\widetilde{F}_k(x)$, i.e.

$$\begin{aligned} \widetilde{F}_k(x) = F(y_0) + \langle \zeta _0, x-y_0 \rangle + \frac{\mu '}{2}|x-y_0|^2. \end{aligned}$$

(7.15)

Let $y\in \partial B_{k+1}\cap [x,y_0]$ and observe that $[y,x]\cap B_R = \emptyset$ (Fig. 3).

Fig. 3

The construction for the proof of (7.14)

By the equivalent definition (7.12) of $\widetilde{F}_{k+1}$, we get for every $\zeta \in \partial F(y)$

$$\begin{aligned} \widetilde{F}_{k+1}(x)\ge F(y)+\langle \zeta , x-y\rangle + \frac{\mu '}{2}|x-y|^2, \end{aligned}$$

while by (7.6) of Lemma 7.3

$$\begin{aligned} F(y)\ge F(y_0) + \langle \zeta _0, y-y_0\rangle +\mu '\,|y-y_0|^2. \end{aligned}$$

Combining these two inequalities, we get

$$\begin{aligned} \widetilde{F}_{k+1}(x)\ge F(y_0) + \langle \zeta _0, x-y_0\rangle + \frac{\mu '}{2}\,|x-y_0|^2 + A, \end{aligned}$$

(7.16)

where

$$\begin{aligned} A= \langle \zeta _0-\zeta , y-x\rangle + \frac{\mu '}{2}\,|x-y|^2 +\mu '\,|y-y_0|^2 - \frac{\mu '}{2}\,|x-y_0|^2. \end{aligned}$$

(7.17)

If we now use (7.7), we obtain

$$\begin{aligned} \langle \zeta _0-\zeta , y_0-y\rangle \ge 2\,\mu '\,|y_0-y|^2. \end{aligned}$$

Since $y-x=(y_0-y)\,|y-x|/|y_0-y|$, this implies

$$\begin{aligned} \langle \zeta _0-\zeta , y-x\rangle \ge 2\,\mu '\,|y_0-y|\,|y-x|. \end{aligned}$$

By inserting this into (7.17) and observing that $|x-y_0|=|x-y|+|y-y_0|$, we obtain

$$\begin{aligned} A\ge \mu '\,|y_0-y|\,|y-x|+\frac{\mu '}{2}\,|y-y_0|^2. \end{aligned}$$

In view of (7.16), (7.15) and also using the fact that

$$\begin{aligned} |y_0-y|\ge 1 \quad \text{ and }\quad |y-x|\ge |x|-|y|= |x|-(k+1), \end{aligned}$$

this finally implies

$$\begin{aligned} \widetilde{F}_{k+1}(x)\ge \widetilde{F}_k(x)+\mu '\,(|x|-k-1), \end{aligned}$$

and (7.14) is proved.

We now establish the following Lipschitz-type estimate for $\widetilde{F}_k$: for every $x, x'\in \mathbb {R}^N$,

$$\begin{aligned} \left| \widetilde{F}_k(x)-\widetilde{F}_k(x')\right| \le \left( L_k + \frac{\mu '}{2}(|x|+|x'|+2\,k)\right) |x-x'|, \end{aligned}$$

(7.18)

where $L_k$ is the Lipschitz constant of F on $B_k$. Indeed, for every $y\in \overline{B_k}$ and every $\zeta \in \partial F(y)$, we have⁷

$$\begin{aligned}&F(y) +\langle \zeta , x-y\rangle + \frac{\mu '}{2}\,|x-y|^2\, 1_{\mathbb {R}^N{\setminus } B_{2R}}(y) \\&\quad \le F(y) + \langle \zeta , x'-y\rangle + \frac{\mu '}{2}\,|x'-y|^2\, 1_{\mathbb {R}^N{\setminus } B_{2R}}(y) \\&\quad \quad + |\zeta |\,|x-x'| + \frac{\mu '}{2}\,|x-x'|\,(|x|+|x'|+2\,|y|)\\&\quad \le \widetilde{F}_k(x') + \left( L_k + \frac{\mu '}{2}(|x|+|x'|+2\,k)\right) |x-x'|. \end{aligned}$$

By exchanging the role of x and $x'$ we get (7.18).

Let us introduce a family $\{\rho _{\varepsilon }\}_{\varepsilon >0} \subset C^{\infty }_0(B_{\varepsilon })$ of standard smooth mollifiers. For some sequence $\{\varepsilon _k\}_{k\in \mathbb {N}}\subset (0,1/2)$ to be specified later, let us consider

$$\begin{aligned} F_k(x):=\widetilde{F}_k*\rho _{\varepsilon _k}-\frac{1}{k}. \end{aligned}$$

By Lemma 7.1, every $F_k$ is a smooth $\mu '$-uniformly convex function outside $B_{R+1}$ and the sequence $\{F_k\}_{k\in \mathbb {N}}$ uniformly converges on bounded sets to F. It remains to prove that $\{F_k\}_{k\in \mathbb {N}}$ is nondecreasing. By (7.18), for every $x\in \mathbb {R}^N$,

$$\begin{aligned} F_k(x)\le \widetilde{F}_k(x) + \left( L_k + \frac{\mu '}{2}(2\,|x|+\varepsilon _k+2\,k)\right) \varepsilon _k-\frac{1}{k}. \end{aligned}$$

Moreover, by (7.14) we have

$$\begin{aligned} \widetilde{F}_k(x)\le \widetilde{F}_{k+1}(x)-\mu '\,(|x|-k-1)_{+}. \end{aligned}$$

Since $\widetilde{F}_{k+1}$ is convex, by Jensen inequality we also have

$$\begin{aligned} \widetilde{F}_{k+1}(x)\le \widetilde{F}_{k+1}*\rho _{\varepsilon _{k+1}}(x)=F_{k+1}(x)+\frac{1}{k+1}. \end{aligned}$$

Hence in order to have $F_k(x)\le F_{k+1}(x)$ it is sufficient that for every $x\in \mathbb {R}^N$

$$\begin{aligned} \left( L_k + \frac{\mu '}{2}(2\,|x|+\varepsilon _k+2k)\right) \varepsilon _k\le \mu '\,(|x|-k-1)_{+}+\frac{1}{k}-\frac{1}{k+1}. \end{aligned}$$

(7.19)

When $|x|\le 2\,(k+1)$, by recalling that $\varepsilon _k<1/2$ we have

$$\begin{aligned} \left( L_k + \frac{\mu '}{2}(2\,|x|+\varepsilon _k+2\,k)\right) \le \left( L_k + \frac{\mu '}{2}(6\,k+5)\right) , \end{aligned}$$

while for the right-hand side of (7.19)

$$\begin{aligned} \mu '\,(|x|-k-1)_{+} +\frac{1}{k}-\frac{1}{k+1}\ge \frac{1}{k\,(k+1)}. \end{aligned}$$

Hence in this case (7.19) holds true provided

$$\begin{aligned} \varepsilon _k\le \Gamma ^-_k:=\frac{1}{k\,(k+1)}\,\frac{1}{L_k +(6\,k+5)\,\mu '/2}. \end{aligned}$$

(7.20)

When $|x|>2\,(k+1)$, the coefficient in front of $\varepsilon _k$ on the left-hand side of (7.19) can be estimated by

$$\begin{aligned} \left( L_k + \frac{\mu '}{2}(2\,|x|+\varepsilon _k+2\,k)\right) \le \mu '\,|x|+\left( L_k+\mu '\,(k+1)\right) \end{aligned}$$

while for the right-hand side we have

$$\begin{aligned} \mu '\,(|x|-k-1)_{+}+\frac{1}{k} -\frac{1}{k+1}\ge \frac{\mu '}{2}|x|+\frac{1}{k\,(k+1)}. \end{aligned}$$

In that case, by recalling that $\varepsilon _k<1/2$ we only need to take

$$\begin{aligned} \varepsilon _k\le \Gamma ^+_k:=\frac{1}{k\,(k+1)}\,\frac{1}{L_k +\mu '\,(k+1)}. \end{aligned}$$

(7.21)

Observe that both $\{\Gamma ^+_k\}_{k\in \mathbb {N}}$ and $\{\Gamma ^-_k\}_{k\in \mathbb {N}}$ monotonically converge to 0 as k goes to $\infty$. Hence, by choosing any decreasing sequence $\{\varepsilon _k\}_{k\in \mathbb {N}}$ such that

$$\begin{aligned} 0<\varepsilon _k<\min \left\{ \frac{1}{2},\,\Gamma ^-_k,\,\Gamma ^+_k\right\} ,\quad k\in \mathbb {N}, \end{aligned}$$

this satisfies both (7.20) and (7.21) and thus (7.19) is guaranteed. In conclusion, up to relabeling the sequence, $\{F_k\}_{k\in \mathbb {N}}$ satisfies all the required properties. $\square$

Lemma 7.5

Let $F:\mathbb {R}^N\rightarrow \mathbb {R}$ be a convex function, which is $\Phi$-uniformly convex outside the ball $B_R$ for some $R>0$. Then for every $Q>R$ there exists a convex function $F_Q:\mathbb {R}^N\rightarrow \mathbb {R}$ with the following properties:

• (i) $F_Q\equiv F$ in $B_Q$;

• (ii) $F_Q$ is $\mu _Q$-uniformly convex outside the ball $B_R$, with⁸

  $$\begin{aligned} \mu _Q=\min \left\{ 1,\min _{t\in [2\,R, 4\,Q]}\Phi (t)\right\} . \end{aligned}$$

Proof

For every $Q>R$, we define the function $F_Q:\mathbb {R}^N\rightarrow \mathbb {R}$ by

$$\begin{aligned} F_Q(x)=F(x)+\mu _Q\,J_Q(x),\quad \text{ where }\quad J_Q(x):=(|x|-Q)_+^2. \end{aligned}$$

Of course, this is a convex function such that $F_Q\equiv F$ in $B_Q$.

In order to verify property ii), we first observe that $\mu _Q\,J_Q$ is $\mu _Q$-uniformly convex outside $B_{2\,Q}$ (see Lemma 7.6 below). We consider again a sequence $\{\rho _{\varepsilon }\}_{\varepsilon >0}\subset C^{\infty }_0(B_{\varepsilon })$ of standard mollifiers. Then for every $\eta \in \mathbb {R}^N$ and every $\xi \in \mathbb {R}^{N}{\setminus } B_{R+\varepsilon }$, we have

$$\begin{aligned} \langle D^2(F_Q*\rho _{\varepsilon })(\xi )\,\eta , \eta \rangle = \langle D^2(F*\rho _{\varepsilon })(\xi )\,\eta , \eta \rangle + \mu _Q\,\langle D^2 (J_Q*\rho _{\varepsilon })(\xi )\,\eta , \eta \rangle . \end{aligned}$$

Since F is $\Phi$-uniformly convex outside $B_R$, the first part of Lemma 7.1 implies that when $\xi \in B_{2\,Q+\varepsilon }{\setminus } B_{R+\varepsilon }$,

$$\begin{aligned} \langle D^2(F*\rho _{\varepsilon })(\xi )\eta , \eta \rangle \ge \left( \min _{t\in [2\,R, 4(Q+\varepsilon )]}\Phi (t)\right) \,|\eta |^2. \end{aligned}$$

Since $\mu _Q\,J_Q$ is $\mu _Q$-uniformly convex outside $B_{2\,Q}$, we get similarly when $\xi \in \mathbb {R}^N{\setminus } B_{2\,Q+\varepsilon }$,

$$\begin{aligned} \mu _Q\,\langle D^2(J_Q*\rho _{\varepsilon })(\xi )\,\eta , \eta \rangle \ge \mu _Q\,|\eta |^2. \end{aligned}$$

In any case, we thus have for every $\xi \in \mathbb {R}^N{\setminus } B_{R+\varepsilon }$

$$\begin{aligned} \langle D^2(F_Q*\rho _{\varepsilon })(\xi )\,\eta , \eta \rangle \ge \left( \min \Big (\mu _Q, \min _{t\in [2\,R, 4(Q+\varepsilon )]}\Phi (t)\Big )\right) \,|\eta |^2. \end{aligned}$$

By the second part of Lemma 7.1, this proves that $F_Q$ is $\mu _Q$-uniformly convex outside $B_R$. $\square$

Lemma 7.6

(A useful function) The function

$$\begin{aligned} {J}_Q(x)=(|x|-Q)_+^2, \end{aligned}$$

is 1-uniformly convex outside the ball $B_{2\,Q}$.

Proof

We first observe that $J_Q$ is $C^2$ outside $B_{Q}$. Thus it is sufficient to compute the Hessian of $J_Q$ in $\mathbb {R}^N{\setminus } B_{2\,Q}$. Let $x\in \mathbb {R}^N{\setminus } B_{2\,Q}$, we have

$$\begin{aligned} D^2 J_Q(x)=2\,\frac{|x|-Q}{|x|}\, \mathrm {Id}_N+2\,\frac{x\otimes x}{|x|^2}-2\,(|x|-Q)\,\frac{x\otimes x}{|x|^3}. \end{aligned}$$

For every $\eta \in \mathbb {R}^N$ we get

$$\begin{aligned}&\langle D^2 J_Q(x)\,\eta ,\eta \rangle =2\,\frac{|x|-Q}{|x|}\,|\eta |^2\\&\quad +2\,\left[ 1-\frac{|x|-Q}{|x|}\right] \,\left( \frac{\langle x,\eta \rangle }{|x|}\right) ^2\ge 2\,\left( 1-\frac{Q}{|x|}\right) \, |\eta |^2, \end{aligned}$$

and thus the conclusion follows, by using that $|x|\ge 2\,Q$. $\square$