Abstract
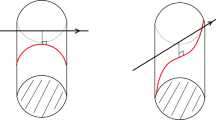
Various properties are given concerning geodesics on, and distance functions from points in, typical degenerate convex surfaces; i.e., surfaces obtained by gluing together two isometric copies of typical (in the sense of Baire category) convex bodies, by identifying the corresponding points of their boundaries.
Similar content being viewed by others
References
Alexandrov A.D. (1955). Die innere Geometrie der konvexen Flächen. Academie-Verlag, Berlin
Birkhoff, G.D.: Dynamical systems. Amer. Math. Soc., Providence, R.I. (1958), rev. edn. 1966
Busemann H. (1958). Convex Surfaces. Interscience Publishers, New York
Burago Y., Gromov M. and Perelman G. (1992). A. D. Alexandrov spaces with curvature bounded below. Russ. Math. Surv. 47: 1–58
Croft H.T., Falconer K.J. and Guy R.K. (1991). Unsolved Problems in Geometry. Springer, New York
Gluck H., Singer, D.: Scattering of geodesic fields I and II. Ann. Math. 108, 347–372 (1978), and 110, 205–225 (1979)
Gruber P. (1977). Die meisten konvexen Körper sind glatt, aber nicht zu glatt. Math. Ann. 229: 259–266
Gruber P. (1988). Minimal ellipsoids and their duals. Rend. Circ. Mat. Palermo 37: 35–64
Gruber P. (1990). Convex billiards. Geom. Dedicata 33: 205–226
Gruber P. (1991). A typical convex surface contains no closed geodesic. J. Reine Angew. Math. 416: 195–205
Gruber, P.: Baire categories in convexity. In: Gruber, P., Wills, J. (eds.) Handbook of Convex Geometry vol. B, 1327–1346. North-Holland, Amsterdam (1993)
Hebda J. (1995). Cut loci of submanifolds in space forms and in the geometries of Möbius and Lie. Geom. Dedicata 55: 75–93
Itoh, J., Rouyer, J., Vîlcu, C.: Antipodal convex hypersurfaces (to appear)
Itoh J. and Vîlcu C. (2004). Farthest points and cut loci on some degenerate convex surfaces. J. Geom. 80: 106–120
Itoh, J., Vîlcu, C.: What do cylinders look like? (to appear)
Klee V.L. (1959). Some new results on smoothness and rotundity in normed linear spaces. Math. Ann. 139: 51–63
Kobayashi S. (1989). On conjugate and cut loci. Global differential geometry. MAA Stud. Math. 27: 140–169
Otsu Y. and Shioya T. (1994). The Riemannian structure of Alexandrov spaces. J. Differ. Geom. 39: 629–658
Rouyer J. (2003). On antipodes on a manifold endowed with a generic Riemannian metric. Pacific J. Math. 212: 187–200
Sakai, T.: Riemannian Geometry. Amer. Math. Soc., Providence, R.I. (1996)
Sen′kin E.P. (1972). Rigidity of convex hypersurfaces (Russian). Ukrain. Geometr. Sb. 12: 131–152
Shiohama, K., Tanaka, M.: Cut loci and distance spheres on Alexandrov surfaces. Actes de la Table Ronde de Géométrie Différentielle (Luminy, 1992), Sém. Congr., vol. 1, Soc. Math. France, pp. 531–559 (1996)
Vîlcu C. (2000). On two conjectures of Steinhaus. Geom. Dedicata 79: 267–275
Vîlcu C. (2006). Properties of the farthest point mapping on convex surfaces. Rev. Roum. Math. Pures Appl. 51: 125–134
Vîlcu C. and Zamfirescu T. (2006). Symmetry and the farthest point mapping on convex surfaces. Adv. Geom. 6: 345–353
Vîlcu C. and Zamfirescu T. (2007). Multiple farthest points on Alexandrov surfaces. Adv. Geom. 7: 83–100
Zamfirescu T. (1980). Nonexistence of curvature in most points of most convex surfaces. Math. Ann. 252: 217–219
Zamfirescu T. (1982). Inscribed and circumscribed circles to convex curves. Proc. Amer. Math. Soc. 80: 455–457
Zamfirescu T. (1982). Many endpoints and few interior points of geodesics. Invent. Math. 69: 253–257
Zamfirescu T. (1984). Points on infinitely many normals to convex surfaces. J. Reine Angew. Math. 350: 183–187
Zamfirescu T. (1991). Baire categories in convexity. Atti. Sem. Mat. Fis. Univ. Modena 39: 139–164
Zamfirescu T. (1992). Long geodesics on convex surfaces. Math. Ann. 293: 109–114
Zamfirescu T. (1995). On some questions about convex surfaces. Math. Nach. 172: 313–324
Zamfirescu T. (1995). Points joined by three shortest paths on convex surfaces. Proc. Amer. Math. Soc. 123: 3513–3518
Zamfirescu T. (1995). Géodésiques et lieux de coupure sur les surfaces convexes typiques. An. Şt. Univ. Ovidius Constanţa 3: 167–173
Zamfirescu T. (1997). Farthest points on convex surfaces. Math. Z. 226: 623–630
Zamfirescu T. (1998). Extreme points of the distance function on convex surfaces. Trans. Amer. Math. Soc. 350: 1395–1406
Zamfirescu T. (2000). Dense ambiguous loci and residual cut loci. Suppl. Rend. Circ. Mat. Palermo, II. Ser. 65: 203–208
Zamfirescu T. (2004). On the cut locus in Alexandrov spaces and applications to convex surfaces. Pacific J. Math. 217: 375–386
Zamfirescu T. (2006). On the number of shortest paths between points on manifolds. Suppl. Rend. Circ. Mat. Palermo. II. Ser. 77: 643–647
Zemlyakov, A.N., Katok, A.B.: Topological transitivity of billiards in polygons. Mat. Zametki 18, 291–300 (1975) (Math. Notes 18, 760–764 (1975))