Abstract
We define Harbater-Mumford subvarieties, which are special kinds of closed subvarieties of Hurwitz moduli spaces obtained by fixing some of the branch points. We show that, for many finite groups, finding geometrically irreducible HM-subvarieties defined over 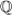 is always possible. This provides information on the arithmetic of Hurwitz spaces and applies in particular to the regular inverse Galois problem with (almost all) fixed branch points. Profinite versions of our results can also be stated, providing new tools to study the geometry of modular towers and the regular inverse Galois problem for profinite groups.
is always possible. This provides information on the arithmetic of Hurwitz spaces and applies in particular to the regular inverse Galois problem with (almost all) fixed branch points. Profinite versions of our results can also be stated, providing new tools to study the geometry of modular towers and the regular inverse Galois problem for profinite groups.
Similar content being viewed by others
References
Bailey, P., Fried, M.: Hurwitz monodromy, spin separation and higher levels of Modular Towers. Proceedings of symposia in pure mathematics, A.M.S., M. Fried and Y. Ihara ed., 2002
Birman, J. S.: Braids, links and mapping class groups. Princeton University Press, 1974
Cadoret, A.: Counting Galois real covers of the projective line. Pacific J. Math. 219, 101–129 (2005)
Cadoret, A.: Théorie de Galois inverse et arithmétique des espaces de Hurwitz. thèse de doctorat de l'U.S.T.L., 2004
Dèbes, P.: Critère de descente pour le corps de définition des G-revêtements de ℙ1. C.R. Acad. Sci. Paris, t.315, série I, 863–868 (1992)
Dèbes, P.: Covers of ℙ1 over the p-adics. in Recent Developments in the Inverse Galois Problem, Contemporary Math. 186, 217–238 (1995)
Dèbes, P.: Modular Towers. construction and diophantine questions, preprint 2004.
Dèbes, P., Deschamps, B.: Corps ψ-libres et théorie inverse de Galois infinie. J. fur die reine und angew. Math. 574, 197–218 (2004)
Dèbes, P., Douai, J.-C., Moret-Bailly, L.: Descent varieties for algebraic covers. J. fur die reine und angew. Math. 574, 51–78 (2004)
Dèbes, P., Emsalem, M.: Harbater-Mumford Components and Towers of Moduli Spaces. J. Inst. Math. Jussieu, to appear.
Dèbes, P., Fried, M.: Nonrigid Constructions in Galois Theory. Pacific J. Math. 163, 81–122 (1994)
Deschamps, B.: Existence de points p-adiques pour tout p sur un espace de Hurwitz. Proceedings AMS-NSF Summer Conference, 186, Cont. Math. series, Recent Developments in the Inverse Galois Problem, 111–171 (1995)
Dickson, L. E.: Linear groups with an exposition of the Galois field theory. Dover, 1958
Fried, M.: Introduction to Modular Towers:Generalizing the relation between dihedral groups and modular curves. Proceedings AMS-NSF Summer Conference. Cont. Math. series, Recent Developments in the Inverse Galois Problem 186, 111–171 (1995)
Fried, M., Volklein, H.: The Inverse Galois Problem and Rational Points on Moduli Spaces. Math. Ann. 290, 771–800 (1991)
Green, B. W., Pop, F., Roquette, P.: On Rumely's Local-Global principle. Jber.d.Dt.Math.-Verein 97, 43–74 (1997)
Harbater, D.: Galois coverings of the arithmetic line. Lecture Notes in Math. 1240, 165–195 (1987)
Harbater, D.: Patching and Galois theory. MSRI Publications series, Cambridge University Press, 41, 313–424 (2003)
Liu, Q.: Tout groupe fini est groupe de Galois sur
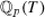 . Contemporary Mathematics. 186, 261–265 (1995)
. Contemporary Mathematics. 186, 261–265 (1995)Matzat, H. B.: Rationality criteria for Galois extensions. in Ihara et al., Galois groups over
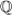 , Proc. Workshop Berkeley 1987, Publ. Math. Sci. Res. Inst. 16, 361–383, Springer, Berlin, Heidelberg, 1989
, Proc. Workshop Berkeley 1987, Publ. Math. Sci. Res. Inst. 16, 361–383, Springer, Berlin, Heidelberg, 1989Malle, G., Matzat, H. B.: Inverse Galois Theory. S.M.M., Springer, Berlin, Heidelberg, 1999
Moret-Bailly, L.: Groupes de Picard et problèmes de Skolem II. Annales Sci. E.N.S., 22, 181–194 (1989)
Pop, F.: Half Riemann's existence theorem. Algebra and Number Theory (G.Frey and J.Ritters, eds.), De Gruyter Proceedings in Mathematics, 1–26 (1994)
Pop, F.: Embedding problems over large fields. Annals of Math. 144, p. 1–35, 1996. Cambridge Studies in Advanced Mathematics, 53, Cambridge University Press, 1999
Suzuki, M.: Group Theory I, II. G.M.W., 247, 248 Springer, Berlin, Heidelberg, 1986
Volklein, H.: Groups as Galois groups - an introduction. Cambridge Studies in Advanced Mathematics, 53, Cambridge University Press, 1999
Wewers, S.: Construction of Hurwitz Spaces. Thesis, Preprint 21 of the IEM, Essen, 1998
Wielandt, H.: Finite Permutation Groups. Academic Press, 1984
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cadoret, A. Harbater-Mumford subvarieties of moduli spaces of covers. Math. Ann. 333, 355–391 (2005). https://doi.org/10.1007/s00208-005-0680-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-005-0680-0



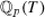 . Contemporary Mathematics. 186, 261–265 (1995)
. Contemporary Mathematics. 186, 261–265 (1995)