$\Gamma$-Limit for Two-Dimensional Charged Magnetic Zigzag Domain Walls

Abstract

Charged domain walls are a type of domain wall in thin ferromagnetic films which appear due to global topological constraints. The non-dimensionalized micromagnetic energy for a uniaxial thin ferromagnetic film with in-plane magnetization $m \in {\mathbb {S}}^1$ is given by

$$\begin{aligned} E_\varepsilon [m] \ = \ \varepsilon \Vert \nabla m\Vert _{L^2}^2 + \frac{1}{\varepsilon } \Vert m \cdot e_2\Vert _{L^2}^2 + \frac{\pi \lambda }{2|\ln \varepsilon |} \Vert \nabla \cdot (m-M)\Vert _{\dot{H}^{-\frac{1}{2}}}^2, \end{aligned}$$

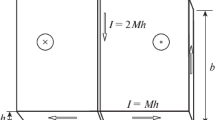
where M is an arbitrary fixed background field to ensure global neutrality of magnetic charges. We consider a material in the form a thin strip and enforce a charged domain wall by suitable boundary conditions on m. In the limit $\varepsilon \rightarrow 0$ and for fixed $\lambda > 0$, corresponding to the macroscopic limit, we show that the energy $\Gamma$-converges to a limit energy where jump discontinuities of the magnetization are penalized anisotropically. In particular, in the subcritical regime $\lambda \leqq 1$, one-dimensional charged domain walls are favorable, in the supercritical regime $\lambda > 1$, the limit model allows for zigzaging two-dimensional domain walls.

Appendix A: Real Space Representation of the Stray Field

We first recall the following standard representation of the homogeneous $H^{\frac{1}{2}}$-norm. We give the short proof since the constant in front of the identity is essential in our arguments:

Lemma A.1

(Finite difference representation of $H^{\frac{1}{2}}$-norm) For $m \in H^{\frac{1}{2}}(Q_\ell )$ we have

$$\begin{aligned} \int _{Q_\ell } \left| |\nabla |^{\frac{1}{2}} m\right| ^2 \ \mathrm{d}x \ = \ \frac{1}{4\pi } \int _{Q_\ell } \int _{\mathbb {R}^2} \frac{|m(x+h)-m(x)|^2}{|h|^3} \ \mathrm{d}h \mathrm{d}x. \end{aligned}$$

(97)

Proof

Using Plancherels identity (8) and Fubini’s theorem, we obtain

$$\begin{aligned}&\int _{Q_\ell } \int _{\mathbb {R}^2} \frac{|m(x+h)-m(x)|^2}{|h|^3} \ \mathrm{d}x \mathrm{d}h = \ \int _{Q_\ell } |{\widehat{m}}(\xi )|^2 \int _{\mathbb {R}^2} \frac{|1-e^{i\xi \cdot h}|^2}{|h|^3} \ \mathrm{d}h \mathrm{d}\xi \\&\quad = \ \int _{Q_\ell } |\xi ||{\widehat{m}}(\xi )|^2 \int _{\mathbb {R}^2} \frac{|1-e^{i\xi \cdot h}|^2}{|h|^3|\xi |} \ \mathrm{d}h \mathrm{d}\xi = \ 4\pi \int _{Q_\ell } |\xi | |{\widehat{m}}(\xi )|^2 \ \mathrm{d}\xi . \end{aligned}$$

The last identity follows with the change of variables $h\mapsto \frac{h}{|\xi |}$ and since $\int _{\mathbb {R}^2} \frac{|1-e^{ih_1}|^2}{|h|^3} \ \mathrm{d}h = 4\pi$ (cf. [13, (39)]). $\square$

The next lemma yields another representation for the $H^{\frac{1}{2}}$-norm when $j \rightarrow - \infty$ and $k \rightarrow \infty$.

Lemma A.2

($H^{\frac{1}{2}}$-norm vs. $H^{-\frac{1}{2}}$-norm) For $f \in C^\infty _c(Q_\ell ;\mathbb {R}^2)$ we have

$$\begin{aligned}&\frac{1}{2} \int \!\!\!\!\int _{\tilde{Q}_\ell \times \tilde{P}_\ell } \frac{|f(y)-f(x)|^2}{|x-y|^3} \ \mathrm{d}x\mathrm{d}y \nonumber \\&\quad = \ \int \!\!\!\!\int _{\tilde{Q}_\ell \times \tilde{P}_\ell } \frac{(\nabla \cdot f)(x)(\nabla \cdot f)(y)}{|x-y|}\ \mathrm{d}x\mathrm{d}y \nonumber \\&\qquad + \int \!\!\!\!\int _{\tilde{Q}_\ell \times \tilde{P}_\ell } \frac{(\nabla \times f)(x)(\nabla \times f)(y)}{|x-y|}\ \mathrm{d}x\mathrm{d}y \nonumber \\&\quad \geqq \ \frac{1}{2} \int \!\!\!\!\int _{\tilde{Q}_\ell \times \tilde{P}_\ell } \frac{(\nabla \cdot f)(x)(\nabla \cdot f)(y)}{|x-y|}\ \mathrm{d}x\mathrm{d}y, \end{aligned}$$

(98)

where $\tilde{Q}_\ell = \mathbb {R}\times [0, \ell )$ and $\tilde{P}_\ell = \mathbb {R}\times [j \ell , k \ell )$ for any $j < k \in \mathbb {Z}$.

Proof

Let I (resp. J) be first (second) integral on the second line of (98). We recall the identity $D (\frac{z}{|z|^3})$ = $D^t (\frac{z}{|z|^3})$ $=$ $\frac{1}{|z|^5}(z^\perp \otimes z^\perp$ − $2 z \otimes z)$ where $z^\perp := (-z_2,z_1)$. Integrating by parts in x and y, since $\nabla _z (\frac{1}{|z|}) = - \frac{z}{|z|^3}$ and since $\nabla (f \cdot g) = (D^t g) f + (D^tf) g$ then yields

$$\begin{aligned} I&= - \int \!\!\!\!\int _{\tilde{Q}_\ell \times \tilde{P}_\ell } f(x) \cdot \frac{y-x}{|x-y|^3} \left[ \nabla _y \cdot (f(y) - f(x))\right] \\&= - \int \!\!\!\!\int _{\tilde{Q}_\ell \times \tilde{P}_\ell } \frac{2 f(x)\cdot (y-x) (f(y)-f(x))\cdot (y-x)}{|x-y|^5} \\&\quad + \frac{f(x) \cdot (y-x)^\perp (f(y)-f(x))\cdot (y-x)^\perp }{|x-y|^5}. \end{aligned}$$

First, integrating in y then in x similarly yields that

$$\begin{aligned} I&= \ \int \!\!\!\!\int _{\tilde{Q}_\ell \times \tilde{P}_\ell } \frac{ 2 f(y)\cdot (y-x) (f(y)-f(x))\cdot (y-x)}{|x-y|^5} \\&- \frac{f(y) \cdot (y-x)^\perp (f(y)-f(x))\cdot (y-x)^\perp }{|x-y|^5}. \end{aligned}$$

Taking the sum of these two expressions, one gets

$$\begin{aligned} I&= \ \int \!\!\!\!\int _{\tilde{Q}_\ell \times \tilde{P}_\ell } \frac{1}{|x-y|^3} \left( \left| (f(y)-f(x))\cdot \frac{y-x}{|y-x|}\right| ^2 - \frac{1}{2} \left| (f(y)-f(x))\cdot \left( \frac{y-x}{|y-x|} \right) ^\perp \right| ^2 \right) . \end{aligned}$$

(99)

Since $\nabla \times f = \nabla \cdot f^\perp$, the same calculation as before, replacing f by $f^\perp$, yields

$$\begin{aligned} J&= \ \int \!\!\!\!\int _{\tilde{Q}_\ell \times \tilde{P}_\ell } \frac{1}{|x-y|^3} \left( \left| (f(y)-f(x))\cdot \left( \frac{y-x}{|y-x|} \right) ^\perp \right| ^2\right. \\&\quad \left. - \frac{1}{2} \left| (f(y)-f(x))\cdot \frac{y-x}{|y-x|} \right| ^2 \right) \ \mathrm{d}x\mathrm{d}y. \end{aligned}$$

The identity (98) follows by taking the sum of the last two equations. The inequality in (98) follows from (99). $\square$

We have the following singular integral characterization for the magnetostatic energy:

Lemma A.3

(Integral representations of magnetostatic energy) Let $\sigma \in L^2(Q_\ell )$ with

$$\begin{aligned} \quad \text {with } {{\,\mathrm{spt}\,}}\sigma \Subset Q_\ell \quad \text { and } \quad \int _{Q_\ell } \sigma \ \mathrm{d}x \ = \ 0. \end{aligned}$$

(100)

Then there is a unique $q \in H^1(Q_\ell ;\mathbb {R}^2)$ with $\nabla \cdot q = \sigma$ and $\nabla \times q = 0$ such that

$$\begin{aligned} \int _{Q_\ell } \left| |\nabla |^{-\frac{1}{2}}\sigma \right| ^2 \ \mathrm{d}x&= \ \frac{1}{4\pi } \int _{Q_\ell } \int _{\mathbb {R}^2} \frac{|q(x+h) - q(x)|^2}{|h|^3} \ \mathrm{d}h \mathrm{d}x \nonumber \\&= \ \frac{1}{2\pi } \lim _{N \rightarrow \infty , N \in \mathbb {N}} \int _{Q_\ell } \int _{\mathbb {R}\times [-N\ell ,N\ell ]}\frac{\sigma (x+h)\sigma (x)}{|h|} \ \mathrm{d}h \mathrm{d}x. \end{aligned}$$

(101)

Proof

By assumption (100) we have ${\widehat{\sigma }}(0) = 0$ and $\nabla {\widehat{\sigma }} \in L^\infty (\mathbb {R}\times \frac{2\pi }{\ell } \mathbb {Z})$. This implies that $q \in H^1(Q_\ell ;\mathbb {R}^2)$, where q is defined by its Fourier transform $\widehat{q} := -i \frac{\xi }{|\xi |^2} {\widehat{\sigma }}$. By construction q satisfies $\nabla \cdot q = \sigma$ and $\nabla \times q = 0$. This solution is unique by the uniqueness of the Helmholtz decomposition. By (9), since $|{\widehat{\sigma }}| = |\xi | |{\widehat{q}}|$ and by (97) we then get

$$\begin{aligned} \int _{Q_\ell } ||\nabla |^{-\frac{1}{2}} \sigma |^2 \ \mathrm{d}\xi \ {\mathop {=}\limits ^{(9)}} \ \int _{\mathbb {R}\times \frac{2\pi }{\ell } \mathbb {Z}} |\xi | |\widehat{q}|^2 \ \mathrm{d}\xi \ {\mathop {=}\limits ^{(97)}} \ \frac{1}{4\pi } \int _{Q_\ell } \int _{\mathbb {R}^2} \frac{|q(x+h)-q(x)|^2}{|h|^3} \ \mathrm{d}h \mathrm{d}x. \end{aligned}$$

Together with Lemma A.2 this yields (101). $\square$