Global Existence and Asymptotic Behavior of Affine Motion of 3D Ideal Fluids Surrounded by Vacuum

Abstract

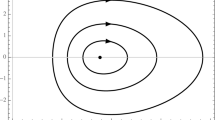
The 3D compressible and incompressible Euler equations with a physical vacuum free boundary condition and affine initial conditions reduce to a globally solvable Hamiltonian system of ordinary differential equations for the deformation gradient in ${{\rm GL}^+(3, \mathbb{R})}$. The evolution of the fluid domain is described by a family of ellipsoids whose diameter grows at a rate proportional to time. Upon rescaling to a fixed diameter, the asymptotic limit of the fluid ellipsoid is determined by a positive semi-definite quadratic form of rank r = 1, 2, or 3, corresponding to the asymptotic degeneration of the ellipsoid along 3−r of its principal axes. In the compressible case, the asymptotic limit has rank r = 3, and asymptotic completeness holds, when the adiabatic index ${\gamma}$ satisfies ${4/3 < \gamma < 2}$. The number of possible degeneracies, 3−r, increases with the value of the adiabatic index ${\gamma}$. In the incompressible case, affine motion reduces to geodesic flow in ${{\rm SL}(3, \mathbb{R})}$ with the Euclidean metric. For incompressible affine swirling flow, there is a structural instability. Generically, when the vorticity is nonzero, the domains degenerate along only one axis, but the physical vacuum boundary condition fails over a finite time interval. The rescaled fluid domains of irrotational motion can collapse along two axes.