1 Introduction

Systems containing electric circuits are described by differential and algebraic equations, which are usually nonlinear. Their solution requires the application of numerical methods that carry out the algebraization of differential equations in integration step. The algebraization of equations for electric circuits by explicit methods is obviously complicated by the error of calculating currents, as a result of which, after multiple calculations, there is a deviation from the first Kirchhoff’s law. The algebraization of these equations by implicit methods is complicated by the error of calculating voltages, as a result of which, after multiple calculations, there is a deviation from the second Kirchhoff’s law. These deviations lead to instability of mathematical models, especially those that are used in conjunction with real objects, and in which the integration step is very small, and the calculation time is very long. Authors faced this problem, during the development of hybrid models. Such problems are mentioned in [1,2,3,4,5,6,7,8,9,10]. In particular, it is noted that most of the electrotechnical objects are stiff systems [1], for which the use of explicit methods is not feasible, since it may cause numerical instability [2, 3, 6, 7]. Reducing the step of numerical integration for stiff systems, if explicit methods are used, slows down the calculation and complicates the real-time implementation of models that interact with real objects [4]. Expediency to use implicit methods for stiff systems is mentioned in [5,6,7,8,9,10,11,12], in particular the trapezoidal method, which is A-stable. At the same time, it is noted in [5] for power systems, that in the case of numerical integration step, increasing the trapezoid method gives a worse result in comparison with the explicit (forward) Euler method. Also, the numerical oscillations of frequency at 1/(2Δt) (Δt—the numerical integration step), which are relevant for trapezoid method in case of stiff systems and which in some cases but not always can be eliminated by decreasing the step value, are noted in [1]. The disadvantage of using the trapezoidal method that appears in numerical oscillations in case of high-frequency current changes in circuits with inductance or their breaks (for example, in case of triggering switches) is indicated in [6, 7]. In addition, implicit methods are known to require additional computations at the integration step, which slows down the calculation. To increase the accuracy of numerical integration, it is required to decrease the step. However, long-term calculations with a small step lead to accumulation of roundoff errors [8] and significant increase of calculation time. To eliminate this contradiction, methods of integrating with a variable step or procedures for changing the integration method during the calculation are proposed in [10, 11]. However, we note that the use of such methods for hybrid models is complicated, since the step in a real-time model is determined by performance of the processor. In addition, in case of the analysis of electric circuits with semiconductor gates, the step change is necessary to find the moment of gate turning-off when the gate current passes through zero.

The peculiarities of using the numerical integration methods for hybrid systems are discussed in [13, 14]. In particular, it is noted the need for numerical integration with the increased step, due to the limited processor performance, as a result of which explicit methods give significant errors. Also, it was noted that using of methods which are absolutely stable for numerical systems was not always stable in case of hybrid systems that contain an analog component (stability in this case depends on the step of numerical integration). According to the analysis carried out in [13], the advantage of using trapezoidal methods and backward differentiation formulas for hybrid systems was claimed, which gives a better result than implicit Euler method, as an example.

These problems are overcame by the authors using the method of average voltage values in the integration step, which ensures the stability of mathematical models in the indicated sense, and is also effective in terms of the amount of calculations. This method appeared as a result of the need to avoid problems in hybrid models of power generation units in which the generator excitation system is a real object, and the power scheme “turbogenerator—block transformer—power line” is a mathematical model. The basis of this method is first described in [15]. The method allows algebraizing differential equations of an electromechanical system with semiconductor converters in the integration step.

The authors for a long time participated in the projects concerned with simulation of electromechanical systems in the field of electric power and transport [16] in the former USSR, Ukraine, Russia, and Poland, in which they used one-step methods of the Runge–Kutta, Adams, and trapezes. To calculate the transients in these projects, the use of mentioned methods was effective. In the real-time models, their operation was limited to 15–20 min, as a result of numerical disturbance related to the algebraization of the equations by the mentioned methods. Thus, using the explicit method, errors arise in the equations that correspond to the first Kirchhoff law, and in case of implicit method—in equations which correspond to the second Kirchhoff law. The problem was solved using the method of average voltage values in the integration step of the second order, which has the features of explicit and implicit methods and simultaneously eliminates mentioned drawbacks of explicit and implicit methods which take place in real-time models of electromechanical systems electric circuits.

Note, that the trapezoidal method, which is widely used in mathematical models, is equivalent in sense of accuracy to the first order method of medium voltage in the integration step, assuming that electrical circuits not include L, C elements connected in series and constraints are linear. In other cases, trapezoidal method is less accurate.

2 Genesis of the method of average voltage values in integration step for the algebraization of the equations for an electric circle

The equations for a branch of an electric circuit containing time dependencies of: electromotive force e(t) source, voltage on resistance Ri(t), induced voltage \(\frac{{{\text{d}}\psi }}{{{\text{d}}t}}\), voltage on capacitance uC(t), and to which voltage u(t) is applied as a result of the influence of the electric circuit for this branch, are as follows:

$$ \begin{gathered} u\left( t \right) - Ri\left( t \right) - \frac{{{\text{d}}\psi }}{{{\text{d}}t}} - u_{C} \left( t \right) + e\left( t \right) = 0, \hfill \\ \frac{{{\text{d}}u_{C} \left( t \right)}}{{{\text{d}}t}} = \frac{i\left( t \right)}{C},\;\psi = f\left( {i,\vec{q}} \right). \hfill \\ \end{gathered} $$
(1)

We accept that in the integration step, Δt, R and C are constant. Flux linkages ψ is a function of the current in a branch and of other factors taken into consideration by the vector of variables \(\vec{q}\).

By integration of the first Eq. (1), the following equation is obtained:

$$ U - U_{R} - U_{C} - U_{L} + E = 0, $$
(2)

where U, UR, UC, UL, and E are the average values of voltages and electromotive force in the integration step Δt:

$$ \begin{gathered} U = \frac{1}{\Delta t}\int\limits_{{t_{0} }}^{{t_{0} + \Delta t}} {u\left( t \right){\text{d}}t} ,\;\;\;U_{R} = \frac{1}{\Delta t}\int\limits_{{t_{0} }}^{{t_{0} + \Delta t}} {u_{R} \left( t \right){\text{d}}t} \hfill \\ U_{C} = \frac{1}{\Delta t}\int\limits_{{t_{0} }}^{{t_{0} + \Delta t}} {u_{C} \left( t \right){\text{d}}t} ,\;\;U_{L} = \frac{1}{\Delta t}\left( {\psi_{1} - \psi_{0} } \right),\;\;E = \frac{1}{\Delta t}\int\limits_{{t_{0} }}^{{t_{0} + \Delta t}} {e\left( t \right){\text{d}}t} . \hfill \\ \end{gathered} $$

Representing the integration for the voltages UR and UC by a Taylor’s series, the following equations are obtained:

$$ \begin{gathered} U + E - u_{R0} - u_{C0} - \sum\limits_{k = 1}^{\infty } {\frac{{\Delta t^{k} }}{{\left( {k + 1} \right)!}}\left( {\frac{{d^{k} u_{R0} }}{{{\text{d}}t^{k} }} + \frac{{d^{k} u_{C0} }}{{dt^{k} }}} \right)} - \frac{1}{\Delta t}\left( {\psi_{1} - \psi_{0} } \right) = 0 \hfill \\ u_{C1} = u_{C0} + \frac{1}{C}\int\limits_{{t_{0} }}^{{t_{0} + \Delta t}} {i{\text{d}}t} = 0. \hfill \\ \end{gathered} $$
(3)

Equation (3) after the transformation is written as:

$$ \begin{gathered} U + E - u_{R0} - u_{C0} + \left( {\frac{R}{m + 1} + \frac{\Delta t}{C} \cdot \frac{{2 - \left( {m + 1} \right)\left( {m + 2} \right)}}{{2\left( {m + 1} \right)\left( {m + 2} \right)}}} \right)i_{0} + \frac{{\psi_{0} }}{\Delta t} \\ - \sum\limits_{k = 1}^{m - 1} {\left( {\frac{{R\Delta t^{k} }}{{\left( {k + 1} \right)!}} \cdot \frac{m - k}{{m + 1}} + \frac{{\Delta t^{k + 1} }}{{C\left( {k + 2} \right)!}} \cdot \frac{{\left( {m + 1} \right)\left( {m + 2} \right) - \left( {k + 1} \right)\left( {k + 2} \right)}}{{\left( {m + 1} \right)\left( {m + 2} \right)}}} \right)\frac{{d^{k} i_{0} }}{{{\text{d}}t^{k} }}} \\ - \left( {\frac{R}{m + 1} + \frac{\Delta t}{{C\left( {m + 1} \right)\left( {m + 2} \right)}}} \right)i_{1} - \frac{{\psi_{1} }}{\Delta t} = 0, \\ u_{C1} = u_{C0} + \frac{\Delta t}{{C\left( {m + 1} \right)}}\left( {mi_{0} + i_{1} } \right) + \sum\limits_{k = 1}^{m - 1} {\frac{{\Delta t^{k + 1} }}{{\left( {k + 1} \right)!}}\frac{1}{C}\frac{m - k}{{m + 1}}} \frac{{d^{k} i_{0} }}{{{\text{d}}t^{k} }} = 0, \\ \end{gathered} $$
(4)

where m is number of members of a Taylor series taken into consideration, which corresponds to the order of the method of average voltages in the integration step. Thus, when m = 1—is the first order method, when m = 2—is the second-order method, etc. When m = 1, the current of the branch in a step is a straight line, and the voltage on the capacitance is a parabola. When m = 2, the current of the branch in a step is a parabola, and the voltage on the capacitance is described by a third-order polynomial.

3 The equation of an electric circle in the method of average voltage values in integration step

The first Eq. (4) corresponds to the one shown in Fig. 1 which is the equivalent circuit, for the analysis of which the methods of the DC circuit theory can be applied. This scheme allows to determine the current of the branch at the end of the integration step.

Fig. 1 E
figure 1

quivalent circuit of the branch

Full size image

This branch is described by the following equations:

$$ \begin{gathered} U - R_{S} i_{1} + E_{S} - \frac{{\psi_{1} }}{\Delta t} = 0 \hfill \\ \psi_{1} = f\left( {i_{1} ,\vec{q}_{1} } \right), \hfill \\ \end{gathered} $$
(5)

where RS is the step resistance of the branch:

$$ R_{S} = \frac{R}{m + 1} + \frac{\Delta t}{{C\left( {m + 1} \right)\left( {m + 2} \right)}}{\text{ - unit of measurement is [}}\Omega {];} $$

ES—is the step electromotive force (e.m.f.), which is determined by the initial conditions for the integration step:

$$ \begin{gathered} E_{S} = E - u_{R0} - u_{C0} + \left( {\frac{R}{m + 1} + \frac{\Delta t}{C} \cdot \frac{{2 - \left( {m + 1} \right)\left( {m + 2} \right)}}{{2\left( {m + 1} \right)\left( {m + 2} \right)}}} \right)i_{0} + \frac{{\psi_{0} }}{\Delta t} \\ - \sum\limits_{k = 1}^{m - 1} {\left( {\frac{{R\Delta t^{k} }}{{\left( {k + 1} \right)!}} \cdot \frac{m - k}{{m + 1}} + \frac{{\Delta t^{k + 1} }}{{C\left( {k + 2} \right)!}} \cdot \frac{{\left( {m + 1} \right)\left( {m + 2} \right) - \left( {k + 1} \right)\left( {k + 2} \right)}}{{\left( {m + 1} \right)\left( {m + 2} \right)}}} \right)\frac{{d^{k} i_{0} }}{{{\text{d}}t^{k} }};} \\ \end{gathered} $$

i1, ψ1, and \(\vec{q}_{1}\) are the variable values at the end of integration step.

The electrical circuit is described by Eq. (5) for each of the branches, as well as by the algebraic equations based on the first Kirchhoff’s law for currents in independent nodes at the end of the integration step. These equations form a system of electric equilibrium equations.

In case of the presence of electrical machines in the system, the equations system is supplemented by magnetic equilibrium equations, as well as by mechanic equilibrium equations, which allow to calculate the flux linkages of the branches based on the currents of the branches and their mutual placement.

In general, the system of equations is nonlinear and is solved by the Newton method. The algorithm for solving by the Newton method will be explained in a simplified example for one branch in which U and \(\vec{q}_{1}\) are known.

To do this, we shall designate:

\(\vec{F}\left( {i_{1} ,\psi_{1} } \right) = \left[ {\begin{array}{*{20}c} {U - R_{S} i_{1} + E_{S} - \frac{{\psi_{1} }}{\Delta t}} \\ {\psi_{1} - \psi_{1} \left( {i_{1} ,\vec{q}_{1} } \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {F_{1} } \\ {F_{2} } \\ \end{array} } \right].\)

The increments of current and flux linkages on each iteration are determined as:

\(\left[ {\begin{array}{*{20}c} {\Delta i_{1} } \\ {\Delta \psi_{1} } \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} {\frac{{\partial F_{1} }}{{\partial i_{1} }}} & {\frac{{\partial F_{1} }}{{\partial \psi_{1} }}} \\ {\frac{{\partial F_{2} }}{{\partial i_{1} }}} & {\frac{{\partial F_{2} }}{{\partial \psi_{1} }}} \\ \end{array} } \right]^{ - 1} \times \left[ {\begin{array}{*{20}c} {F_{1} \left( {i_{1}^{0} ,\psi_{1}^{0} } \right)} \\ {F_{2} \left( {i_{1}^{0} ,\psi_{1}^{0} } \right)} \\ \end{array} } \right],\)where \(i_{1}^{0} ,\psi_{1}^{0}\) are zeroth approximations for the current and flux linkage:

$$ \begin{gathered} F_{1} \left( {i_{1}^{0} ,\psi_{1}^{0} } \right) = U - R_{S} i_{1}^{0} + E_{S} - \frac{{\psi_{1}^{0} }}{\Delta t}, \hfill \\ F_{2} \left( {i_{1}^{0} ,\psi_{1}^{0} } \right) = \psi_{1}^{0} - \psi_{1} \left( {i_{1}^{0} ,\vec{q}} \right), \hfill \\ \end{gathered} $$

\(\frac{{\partial F_{1} }}{{\partial i_{1} }} = - R_{S}\), \(\frac{{\partial F_{1} }}{{\partial \psi_{1} }} = - \frac{1}{\Delta t}\), \(\frac{{\partial F_{2} }}{{\partial i_{1} }} = - \frac{{{\text{d}}\psi_{1} \left( {i_{1} ,\vec{q}_{1} } \right)}}{{{\text{d}}i_{1} }} = - L^{\partial }\)—is the dynamic inductance of the electric branch as a function of current i1, \(\frac{{\partial F_{2} }}{{\partial \psi_{1} }} = 1\).

Therefore:

$$ \left[ {\begin{array}{*{20}c} {\Delta i_{1} } \\ {\Delta \psi_{1} } \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} { - R_{S} } & { - \frac{1}{\Delta t}} \\ { - L^{\partial } } & 1 \\ \end{array} } \right]^{ - 1} \times \left[ {\begin{array}{*{20}c} {F_{1} \left( {i_{1}^{0} ,\psi_{1}^{0} } \right)} \\ {F_{2} \left( {i_{1}^{0} ,\psi_{1}^{0} } \right)} \\ \end{array} } \right]. $$
(6)

The values of current and flux linkage at the first approximation are written as:

$$ \left[ {\begin{array}{*{20}c} {i_{1}^{1} } \\ {\psi_{1}^{1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {i_{1}^{0} } \\ {\psi_{1}^{0} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\Delta i_{1} } \\ {\Delta \psi_{1} } \\ \end{array} } \right]. $$
(7)

The next approximation is implemented according to the algorithm described for the previous approximation. If the flux linkage is a linear function of current, the algorithm is reduced to a single zeroth iteration.

4 Application of the method of average voltage values in integration step

4.1 Description of the scheme

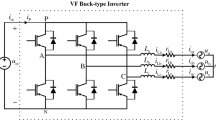
The described method was repeatedly used by the authors to create hybrid models that combine physical and computer (digital) parts. One example was the model of power generation system of the ship's power plant with a diesel generator. The digital component of the hybrid model (Fig. 2) is power conversion system that contains the synchronous generator G, driven by a diesel engine D with a speed control system, as well as an autonomous load consisting of the synchronous machine G2 and RL branches. The physical part of the hybrid model is the real generator’s excitation controller of type Digital AVR DECS 200 with an automatic voltage regulator. The signals of voltage Ug and stator’s current Ig of generator are emitted from the computer model to the physical excitation controller. The output control signal of the pulse-width converter, which forms the pulse excitation voltage of generator, is sent to the computer model from the excitation controller. For the transmission of signals between physical and digital parts, the galvanic separation devices were used; these are not shown in the diagram.

Fig. 2
figure 2

Functional scheme of the hybrid model of the power generation system of the ship's power plant

Full size image

4.2 The calculation of voltages and derivatives of currents

The calculation scheme of the power conversation system implemented by the digital model is shown in Fig. 3. This scheme is used for calculation of voltages and current derivative. The scheme consists of six branches that simulate the phases A, B, and C of the stator winding, the excitation winding, and the damping system (the damping system is modeled by two short-circuited RL branches on the axes d and q) of synchronous generator. The inductance and resistance of load are taken into consideration in the inductances and resistances of the stator windings. In addition, the branches of stator windings contain capacitors which take into consideration the load capacity.

Fig. 3
figure 3

Calculation scheme of the power conversation system for the calculation of voltages and derivatives of currents

Full size image

The authors use the second-order method of averages voltages in integration step (m = 2). This method requires the calculation of currents derivative in the branches.

The presented scheme is described by the following vector equation according to the second Kirchhoff's law:

$$ \vec{u} - {\mathbf{R}}\vec{i} - \vec{e}_{tr} - \vec{e}_{r} - \vec{u}_{C} + \vec{e} = 0, $$
(8)

where \(\vec{u} = \left( {u_{A} ,u_{B} ,u_{C} ,u_{f} ,u_{D} ,u_{Q} } \right)^{T}\)—is the vector of the voltages on the branches; \(\vec{i} = \left( {i_{A} ,i_{B} ,i_{C} ,i_{f} ,i_{D} ,i_{Q} } \right)^{T}\)—is the vector of the currents in the branches; \(\vec{e}_{{{\text{tr}}}} = {\mathbf{L}}^{\partial } \frac{{{\text{d}}\vec{i}}}{{{\text{d}}t}}\)—is the vector of the transformation e.m.f., \({\mathbf{L}}^{\partial }\)—is the matrix of the dynamic inductances of the branches; \(\vec{e}_{r} = p\omega \frac{{{\text{d}}{\mathbf{L}}}}{{{\text{d}}\gamma }}\vec{i}\)—is the vector of the rotation e.m.f., L—is the matrix of the static inductances of the branches, ω—is the angular speed, p—is the number of pairs of the poles, γ—is the rotation angle; \(\vec{u}_{C} = \left( {u_{CA} ,u_{CB} ,u_{CC} ,0,0,0} \right)^{T}\)—is the vector of the voltages on the capacitors; \(\vec{e} = \left( {0,0,0,e_{f} ,0,0} \right)^{T}\)—is the vector of the e.m.f. applied to the branches.

The relation between the voltages on the branches and the potentials of the independent nodes v is described by the following expression:

$$ \vec{u} = {{\varvec{\Pi}}}^{T} v, $$
(9)

where \({{\varvec{\Pi}}} = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 0 & 0 & 0 \\ \end{array} } \right]\)—is the incidence matrix.

Equations for the derivatives of currents according to Kirchhoff's first law is as follows:

$$ {{\varvec{\Pi}}}\frac{{{\text{d}}\vec{i}}}{{{\text{d}}t}} = 0. $$
(10)

From Eqs. (8) and (9), the derivatives of currents are obtained:

$$ \frac{{{\text{d}}\vec{i}}}{{{\text{d}}t}} = {\mathbf{L}}^{\partial - 1} \left( {{{\varvec{\Pi}}}^{T} v - {\mathbf{R}}\vec{i} - p\omega \frac{{{\text{d}}{\mathbf{L}}}}{{{\text{d}}\gamma }}\vec{i} - \vec{u}_{C} + \vec{e}} \right) $$
(11)

After substitution (11) into (10), the following equation is obtained:

$$ {{\varvec{\Pi}}} \cdot {\mathbf{L}}^{\partial - 1} {{\varvec{\Pi}}}^{T} v - {{\varvec{\Pi}}} \cdot {\mathbf{L}}^{\partial - 1} \left( {{\mathbf{R}}\vec{i} + p\omega \frac{{{\text{d}}{\mathbf{L}}}}{{{\text{d}}\gamma }}\vec{i} + \vec{u}_{C} - \vec{e}} \right) = 0. $$
(12)

The potential of the independent node v is determined from Eq. (12), and then, the voltage on the branches is determined from Eq. (9) and the derivatives of the currents are determined from Eq. (11).

4.3 The calculation of the currents by the method of averages voltages in integration step

The calculation scheme of the power conversion system, taking into consideration the statements of the method of average voltage in integration step, is shown in Fig. 4.

Fig. 4
figure 4

Calculation scheme of the power conversation system for the current calculation

Full size image

If given (5), the vector equation for this scheme is as follows:

$$ \vec{U} + \vec{E}_{S} - {\mathbf{R}}_{S} \vec{i}_{1} - \frac{{\vec{\psi }_{1} }}{\Delta t} = 0, $$
(13)

where the matrix of step resistance:

$$ {\mathbf{R}}_{S} = {\text{diag}}\left[ {\frac{{R_{A} }}{3} + \frac{\Delta t}{{12C_{A} }},\frac{{R_{B} }}{3} + \frac{\Delta t}{{12C_{B} }},\frac{{R_{C} }}{3} + \frac{\Delta t}{{12C_{C} }},\frac{{R_{f} }}{3},\frac{{R_{D} }}{3},\frac{{R_{Q} }}{3}} \right], $$
(14)

in which RA, RB, and RC are the total resistances of branches consisting of the stator winding and generator load; Rf is the resistance of the excitation winding; RD and RQ are the resistances of branches represented the synchronous machine damping system; vector of the step e.m.f:

$$ \vec{E}_{S} = \left[ {\begin{array}{*{20}c} { - u_{RA0} - u_{CA0} + \left( {\frac{{R_{A} }}{3} - \frac{5\Delta t}{{12C_{A} }}} \right)i_{A0} + \frac{{\psi_{A0} }}{\Delta t} - \left( {\frac{{R_{A} \Delta t}}{6} + \frac{{\Delta t^{2} }}{{12C_{A} }}} \right)\frac{{{\text{d}}i_{A} }}{{{\text{d}}t}}} \\ { - u_{RB0} - u_{CB0} + \left( {\frac{{R_{B} }}{3} - \frac{5\Delta t}{{12C_{B} }}} \right)i_{B0} + \frac{{\psi_{B0} }}{\Delta t} - \left( {\frac{{R_{B} \Delta t}}{6} + \frac{{\Delta t^{2} }}{{12C_{B} }}} \right)\frac{{{\text{d}}i_{B} }}{{{\text{d}}t}}} \\ { - u_{RC0} - u_{CC0} + \left( {\frac{{R_{C} }}{3} - \frac{5\Delta t}{{12C_{A} }}} \right)i_{C0} + \frac{{\psi_{C0} }}{\Delta t} - \left( {\frac{{R_{C} \Delta t}}{6} + \frac{{\Delta t^{2} }}{{12C_{C} }}} \right)\frac{{{\text{d}}i_{C} }}{{{\text{d}}t}}} \\ {E_{f} - u_{Rf0} + \frac{{R_{f} }}{3}i_{f0} + \frac{{\psi_{f0} }}{\Delta t} - \frac{{R_{f} \Delta t}}{6}\frac{{{\text{d}}i_{f} }}{{{\text{d}}t}}} \\ { - u_{RD0} + \frac{{R_{D} }}{3}i_{D0} + \frac{{\psi_{D0} }}{\Delta t} - \frac{{R_{D} \Delta t}}{6}\frac{{{\text{d}}i_{D} }}{{{\text{d}}t}}} \\ { - u_{RQ0} + \frac{{R_{Q} }}{3}i_{Q0} + \frac{{\psi_{Q0} }}{\Delta t} - \frac{{R_{Q} \Delta t}}{6}\frac{{{\text{d}}i_{Q} }}{{{\text{d}}t}}} \\ \end{array} } \right]; $$
(15)

the vector of flux linkages (value at the end of the integration step):

$$ \vec{\psi }_{1} = \left( {\psi_{A1} ,\psi_{B1} ,\psi_{C1} ,\psi_{f1} ,\psi_{D1} ,\psi_{Q1} } \right)^{T} ; $$

the vector of flux linkages (value at the beginning of the integration step):

$$ \vec{\psi }_{0} = \left( {\psi_{A0} ,\psi_{B0} ,\psi_{C0} ,\psi_{f0} ,\psi_{D0} ,\psi_{Q0} } \right)^{T} ; $$

the vector of currents (value at the end of the integration step):

$$ \vec{i}_{1} = \left( {i_{A1} ,i_{B1} ,i_{C1} ,i_{f1} ,i_{D1} ,i_{Q1} } \right)^{T} ; $$

the vector of the average at the integration step values of voltage:

$$ \vec{U} = \left( {U_{A} ,U_{B} ,U_{C} ,U_{f} ,U_{D} ,U_{Q} } \right)^{T} . $$

Equation (13) is supplemented by the equation for the currents according to Kirchhoff’s first law:

$$ {{\varvec{\Pi}}}\vec{i} = 0, $$
(16)

where \({{\varvec{\Pi}}} = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 0 & 0 & 0 \\ \end{array} } \right]\)—is the incident matrix.

The flux linkages in Eq. (13) are a function of the currents and the rotation angle γ:

$$ \vec{\psi }_{1} = f\left( {\vec{i}_{1} ,\gamma } \right). $$
(17)

The relation between the average in the integration step values of the branch voltages and the potentials of independent nodes is described by the equations:

$$ \vec{U} = {\mathbf{\Pi }}^{T} V,\;\;V = \frac{1}{{\Delta t}}\int\limits_{{t_{0} }}^{{t_{0} + \Delta t}} {\upsilon {\text{d}}t}$$
(18)

The system of Eqs. (13), (16)–(18) is a mathematical model of the presented system. This system of equations is nonlinear and Newton's method is used to solve it.

Denote for initial approximation:

$$ \vec{U}^{0} + \vec{E}_{S} - {\mathbf{R}}_{S} \vec{i}_{1}^{0} - \frac{{\vec{\psi }_{1}^{0} }}{\Delta t} = F_{1}^{0} , $$
(19)
$$ {{\varvec{\Pi}}}\vec{i}_{1}^{0} = F_{2}^{0} , $$
(20)

where:

$$ \vec{\psi }_{1}^{0} = {\mathbf{L}}\vec{i}_{1}^{0} ,\vec{U}^{0} = {{\varvec{\Pi}}}^{T} V^{0} .$$
(21)

The vector equation for sequential approximations is as follows:

$$ \vec{F}^{0} + \frac{{{\text{d}}\vec{F}}}{{{\text{d}}\vec{x}}}\Delta \vec{x} = 0, $$
(22)

where \(\vec{F} = \left[ {\begin{array}{*{20}c} {F_{1} } \\ {F_{2} } \\ \end{array} } \right]\), \(\vec{x} = \left[ {\begin{array}{*{20}c} {\vec{i}_{1} } \\ V \\ \end{array} } \right],\)

The increments of currents and average on the step value of voltage (potential of an independent node) on each iteration are determined as:

\(\Delta \vec{x} = \left[ {\begin{array}{*{20}c} {\Delta \vec{i}_{1} } \\ {\Delta V} \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} {\frac{{\partial F_{1} }}{{\partial \vec{i}_{1} }}} & {\frac{{\partial F_{1} }}{\partial V}} \\ {\frac{{\partial F_{2} }}{{\partial \vec{i}_{1} }}} & {\frac{{\partial F_{2} }}{\partial V}} \\ \end{array} } \right]^{ - 1} \times \left[ {\begin{array}{*{20}c} {F_{1}^{0} } \\ {F_{2}^{0} } \\ \end{array} } \right],\)where \(\frac{{\partial F_{1} }}{{\partial \vec{i}_{1} }} = - {\mathbf{R}}_{S} - \frac{1}{\Delta t}{\mathbf{L}}^{\partial } = {\mathbf{G}}\), \(\frac{{\partial F_{1} }}{\partial V} = {{\varvec{\Pi}}}^{T}\), \(\frac{{\partial F_{2} }}{{\partial \vec{i}_{1} }} = {{\varvec{\Pi}}}\), \(\frac{{\partial F_{2} }}{\partial V} = 0\).

Thus, Eq. (22) is written as:

$$ \begin{gathered} {\mathbf{G}}\Delta \vec{i}_{1} + {{\varvec{\Pi}}}^{T} \Delta V + F_{1}^{0} = 0 \hfill \\ {{\varvec{\Pi}}}\Delta \vec{i}_{1} + F_{2}^{0} = 0. \hfill \\ \end{gathered} $$
(23)

From the system of Eq. (23), the following equation is obtained:

$$ {\mathbf{G}}_{S} \Delta V + {\mathbf{C}}_{S} = 0, $$
(24)

where

$$ {\mathbf{G}}_{S} = {{\varvec{\Pi}}} \cdot {\mathbf{G}}^{ - 1} \cdot {{\varvec{\Pi}}}^{T} ,{\mathbf{C}}_{S} = {{\varvec{\Pi}}} \cdot {\mathbf{G}}^{ - 1} F_{1}^{0} - F_{2}^{0} . $$
(25)

The algorithm of mathematical modeling is cyclic and consists of the following actions:

  • Set initial conditions (values of variables at the beginning of the step).

  • Define the parameters of the scheme in the step: \({\mathbf{R}}_{S}\), \(\vec{E}_{S}\).

  • Set the zeroth approximations for the currents \(\vec{i}_{1}^{0}\) and the average potential \(V^{0}\) (for example, it can be equal to the values at the beginning of the step).

    • From (21), \(\vec{\psi }_{1}^{0}\), \(\vec{U}^{0}\) are calculated.

    • From (19) and (20), \(F_{1}^{0}\) and \(F_{2}^{0}\) are obtained. If \(\left| {F_{1}^{0} } \right| < \varepsilon\) and \(\left| {F_{2}^{0} } \right| < \varepsilon\) so, go to the next step of the calculation. Otherwise, proceed to the 3.3 and 3.4.

    • From Eq. (23) and (24), the increments \(\Delta V\) and \(\Delta \vec{i}_{1}\) are calculated.

    • The variables at the end of the iteration \(V^{1} = V^{0} + \Delta V\), \(\vec{i}_{1}^{1} = \vec{i}_{1}^{0} + \Delta \vec{i}_{1}\) are calculated. Proceeding to 3.1 with the changing of initial approximations.

After determining of the currents, the voltages on the capacitors are determined as:

\(u_{CA1} = u_{CA0} + \frac{\Delta t}{{3C_{A} }}\left( {2i_{A0} + i_{A1} } \right) + \frac{{\Delta t^{2} }}{{6C_{A} }}\frac{{{\text{d}}i_{A0} }}{{{\text{d}}t}},\)

\(u_{CB1} = u_{CB0} + \frac{\Delta t}{{3C_{B} }}\left( {2i_{B0} + i_{B1} } \right) + \frac{{\Delta t^{2} }}{{6C_{B} }}\frac{{{\text{d}}i_{B0} }}{{{\text{d}}t}},\)

\(u_{Cc1} = u_{Cc0} + \frac{\Delta t}{{3C_{c} }}\left( {2i_{c0} + i_{c1} } \right) + \frac{{\Delta t^{2} }}{{6C_{c} }}\frac{{{\text{d}}i_{c0} }}{{{\text{d}}t}}.\)

4.4 The modeling results

Figures 5, 6, 7, 8, 9 shows the results obtained on the developed hybrid model, compared with the results of a physical experiment on a laboratory plant where the synchronous generator of type GCf84a/4, 27 kVA was used. The research was carried out for the regime of initial excitation of the generator without a load (Figs. 5, 6), for the load decrementing (Fig. 7), and for the load incrementing (Fig. 8) regimes, as well as for the steady-state regime (Fig. 9). The presented oscillograms show a high convergence of the results obtained on the hybrid model and on the physical plant. In particular, the maximum deviation is near 9%, and the average deviation is near 6%.

Fig. 5
figure 5

Generator's output voltage (instantaneous values) during the initial excitation: a computer simulation; b experiment (the measurement sampling corresponds to 150,000 points per 6 s)

Full size image
Fig. 6
figure 6

Generator's excite current during the initial excitation: a computer simulation; b experiment (the measurement sampling corresponds to 150,000 points per 6 s)

Full size image
Fig. 7
figure 7

Generator's excite current during the load dropping: a computer simulation; b experiment (the measurement sampling corresponds to 100,000 points per 4 s)

Full size image
Fig. 8
figure 8

Generator's excite current during the load-on: a computer simulation; b experiment (the measurement sampling corresponds to 100,000 points per 4 s)

Full size image
Fig. 9
figure 9

Excite voltage uf and current if in steady-state regimes and after loss of excitation: a computer simulation; b experiment (the measurement sampling corresponds to 100,000 points per 4 s)

Full size image

The other example of using the method of average voltages in the integration step is described in [17]. In this case, the developed nonlinear mathematical model is used for synthesis of fuzzy-control system for a power generation unit.

5 Conclusions

The application of the method of average voltages in the integration step to algebraize the differential equations describing the electrical circuits ensures the stability of mathematical models in their computer applications.

The combination of the method of average voltages in the integration step with the Newton method for solving systems of nonlinear algebraic equations allows to effectively simulate processes in nonlinear electromechanical systems.

In case of using the method in real-time models, the discretization step is determined by two factors: the rate of change of variables and the sampling of the signals in the physical part of the hybrid model. Within the physical signal sample, the step for the second-order method determines the time range in which the currents are described by the second-order polynomial and the voltages on the capacitances are described by the third-order polynomial.

The presented example is one of the numerous projects developed by the authors in the field of modeling of electromechanical systems.