Skip to main content

Advertisement

SpringerLink
Log in

Robust design of multimachine power system stabilizers based on improved non-dominated sorting genetic algorithms

  • Original Paper
  • Published:
Electrical Engineering Aims and scope Submit manuscript

Abstract

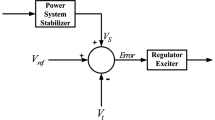
Power system stabilizers (PSSs) associated with generators are mandatory requirements for damping low-frequency oscillations of a multimachine power system. Nevertheless, PSSs work well at particular network configuration and steady-state conditions for which they were designed. Therefore, the aim of this paper is the design of a robust PSS able to ensure the stability of the system for a wide range of loading conditions and various faults with higher performance. The main motivation for this design is to simultaneously shift as much as could be possible the lightly damped and undamped system electromechanical modes, at different loading conditions and system configurations, into pre-specified zone in the s-plane called D-shape sector. Hence, the problem of robustly tuning the PSSs parameters is formulated as a multiobjective optimization problem (MOP) with an eigenvalue-based objective functions. An improved version of non-dominated sorting genetic algorithms (NSGAII) is proposed to solve this MOP. The performance of the proposed NSGAII-based PSS (NSGAII-PSS) under different loading conditions, system configurations and disturbances is tested and examined for different multimachine power systems. Eigenvalue analysis and nonlinear simulations show the effectiveness and robustness of the proposed controllers NSGAII-PSSs and their ability to provide efficient damping of low-frequency oscillations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Kundur P (1994) Power system stability and control. McGraw-Hill, New York

    Google Scholar 

  2. Pai MA, Sen Gupta DP, Padiyar KR (2004) Small signal analysis of power systems. Narosa Publishing House, New Delhi

    Google Scholar 

  3. Bikash P, Bakarko C (2005) Robust control in power systems. Springer, New York

    Google Scholar 

  4. Abido MA (2000) Robust design of multimachine power system stabilizers using simulated annealing. IEEE Trans Energy Convers 15(3):297–304

    Article  Google Scholar 

  5. Abdel-Magid YL, Abido MA (2004) Robust coordinated design of excitation and TCSC-based stabilizers using genetic algorithms. Int J Electr Power Energy Syst 69(2–3):129–141

    Article  Google Scholar 

  6. Ekinci S, Demiroren A (2015) PSO based PSS design for transient stability enhancement. IU J Electr Electron Eng 15(1):1855–1862

    Google Scholar 

  7. Panda S, Padhy NP, Patel RN (2007) Robust coordinated design of PSS and TCSC using PSO technique for power system stability enhancement. J Electr Syst 3(2):109–123

    Google Scholar 

  8. Da Cruz JJ, Zanetta LC (1997) Stabilizer design for multimachine power systems using mathematical programming. Int J Electr Power Energy Syst 19(8):519–523

    Article  Google Scholar 

  9. Maslennikov VA, Ustinov SM (1996) The optimization method for coordinated tuning of power system regulators. In: Proceedings of the 12th power system computation conference PSCC, Dresden, pp 70–75

  10. Abdel-Magid YL, Abido MA, Al-Baiyat S, Mantawy AH (1999) Simultaneous stabilization of multimachine stabilizers via genetic algorithm. IEEE Trans Power Syst 14(4):1428–1439

    Article  Google Scholar 

  11. Abdel-Magid YL, Abido MA (2003) Optimal multi-objective design of robust power system stabilizers using genetic algorithms. IEEE Trans Power Syst 18(3):1125–1132

    Article  Google Scholar 

  12. Sebaa K, Boudour M (2009) Optimal locations and tuning of robust power system stabilizer using genetic algorithms. Int J Electr Power Syst Res 79(2):406–416

    Article  MATH  Google Scholar 

  13. Ghasemi A, Shayeghi H, Alkhatib H (2013) Robust design of multimachine power system stabilizers using fuzzy gravitational search algorithm. Int J Electr Power Energy Syst 51:190–200

    Article  Google Scholar 

  14. Beno MM, Singh NA, Therase MC, Ibrahim MMS (2011) Design of PSS for damping low frequency oscillations using bacteria foraging tuned non-linear neuro-fuzzy controller. In: Proceedings of the IEEE GCC conference and exhibition, pp 653–656

  15. Mishra S, Tripathy M, Nanda J (2007) Multimachine power system stabilizer design by rule based bacteria foraging. Int J Electr Power Syst Res 77(12):1595–1607

    Article  Google Scholar 

  16. Abd-Elazim SM, Ali ES (2013) A hybrid particle swarm optimization and bacterial foraging for optimal power system stabilizers design. Int J Electr Power Syst Res 46:334–341

    Article  Google Scholar 

  17. Fereidouni AR, Vahidi B, Hoseini Mehr T, Tahmasbi M (2013) Improvement of low frequency oscillation damping by allocation and design of power system stabilizers in the multi-machine power system. Int J Electr Power Energy Syst 52:207–220

    Article  Google Scholar 

  18. Guesmi T, Hadj Abdallah H, Toumi A (2006) New approach to solve multiobjective environmental/economic dispatch. J Electr Syst 2(2):64–81

    Google Scholar 

  19. Abido MA (2006) Multiobjective evolutionary algorithms for electric power dispatch problem. IEEE Trans Evol Comput 10(3):315–329

    Article  Google Scholar 

  20. Alexandre HFD, Vasconcelos JA (2002) Multiobjective genetic algorithms applied to solve optimization problems. IEEE Trans Magn 38(2):1133–1136

    Article  Google Scholar 

  21. Yassami H, Darabi A, Rafiei SMR (2010) Power system stabilizer design using strength pareto multi-objective optimization approach. Int J Electr Power Syst Res 80:838–846

    Article  Google Scholar 

  22. Zitzler E, Thiele L (1991) Multiobjective evolutionary algorithms: A comparative case study and the strength pareto approach. IEEE Trans Evol Comput 3(4):257–271

    Article  Google Scholar 

  23. Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6(2):182–197

    Article  Google Scholar 

  24. Ramesh S, Kannanb S, Baskar S (2012) Application of modified NSGA-II algorithm to multi-objective reactive power planning. Appl Soft Comput 12:741–753

    Article  Google Scholar 

  25. Herrera F, Lozano M, Verdegay JL (1998) Tackling real-coded genetic algorithms: operators and tools for behavioral analysis. Artif Intell Rev 12(4):265–319

    Article  MATH  Google Scholar 

  26. Anderson PM, Fouad AA (1977) Power system control and stability. Iowa State Univ Press, Iowa

    Google Scholar 

  27. Pai MA (1989) Energy function analysis for power system stability. Kluwer Academic Publishers, Berlin

    Book  Google Scholar 

  28. Farah A, Guesmi T, Hadj Abdallah H, Ouali A (2016) A novel chaotic teaching-learning-based optimization algorithm for multi-machine power system stabilizers design problem. Int J Electr Power Energy Syst 77:197–209

    Article  Google Scholar 

  29. Labdelaoui H, Boudjemaa F, Boukhetala D (2016) multiobjective tuning approach of power system stabilizers using particle swarm optimization. Turk J Electr Eng Comput Sci 24:3898–3909

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Engineering, University of Hail, Hail, Saudi Arabia

    T. Guesmi

  2. National Engineering School of Sfax, Sfax University, 3038, Sfax, Tunisia

    T. Guesmi, A. Farah, H. Hadj Abdallah & A. Ouali

Authors
  1. T. Guesmi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Farah
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. H. Hadj Abdallah
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. A. Ouali
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to T. Guesmi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guesmi, T., Farah, A., Abdallah, H.H. et al. Robust design of multimachine power system stabilizers based on improved non-dominated sorting genetic algorithms. Electr Eng 100, 1351–1363 (2018). https://doi.org/10.1007/s00202-017-0589-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00202-017-0589-0

Keywords

Search

Navigation