Capital accumulation game with quasi-geometric discounting and consumption externalities

Abstract

This study introduces quasi-geometric discounting into a simple growth model of common capital accumulation that takes consumption externalities into account. We examine how present bias affects economic growth and welfare, and we consider two equilibrium concepts: the non-cooperative Nash equilibrium (NNE) and the cooperative equilibrium (CE). We show that the growth rate in the NNE can be higher than that in the CE if individuals strongly admire the consumption of others regardless of the magnitude of present bias. Contrary to the results in the time-consistent case, we show that, when present bias is incorporated, the welfare level in the NNE can be higher than that in the CE in the initial period. However, in later periods, this relationship can be reversed depending on the difference in the speed of capital accumulation.

Appendices

Appendices

1.1 A. Proof of Proposition 1

$0<\sigma ^n<A/N$ must be satisfied because $k^{\prime }=(A-N\sigma ^n)k>0$. We denote the left (right)-hand side of (14) as $f(\sigma ^n)$ ($g(\sigma ^n)$). Differentiating $f(\sigma ^n)$ with respect to $\sigma ^n$ leads to

$$\begin{aligned} f^\prime (\sigma ^n) =N (\psi -1) (A- N \sigma ^n)^{-\psi }<0. \end{aligned}$$

Note that $\psi <1$. Differentiating $f^\prime (\sigma ^n)$ with respect to $\sigma ^n$ results in

$$\begin{aligned} f^{\prime \prime }(\sigma ^n) =N^2 \psi (\psi -1) (A- N \sigma ^n)^{-\psi -1} {\left\{ \begin{array}{ll}>0 &{} \text {when }0<\eta<1, \\ <0 &{} \text {when }\eta >1. \end{array}\right. } \end{aligned}$$

Note that when $0<\eta <1$, $\psi <0$ holds. On the other hand, when $\eta >1$, $0<\psi <1$ holds. Moreover, $f(0)=A^{1-\psi }$ and $f(A/N)=0$ hold. Differentiating $g(\sigma ^n)$ with respect to $\sigma ^n$ leads to

$$\begin{aligned} g^\prime (\sigma ^n) = -\{ N-\beta (1-\alpha )\}\delta {\left\{ \begin{array}{ll}<0 &{} \text {when }N>\beta (1-\alpha ), \\ >0 &{} \text {when }N<\beta (1-\alpha ). \end{array}\right. } \end{aligned}$$

(A1)

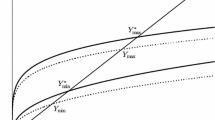
Moreover, $g(0)=A\delta$ and $g(A/(N-\beta (1-\alpha )))=0$ hold. Note that when $N>\beta (1-\alpha )$, $A/(N-\beta (1-\alpha ))>A/N$ holds. On the other hand, when $N<\beta (1-\alpha )$, $A/(N-\beta (1-\alpha ))<0$ holds. From these results, we can graphically examine the existence of the NNE. Figure 5 shows $f(\sigma ^n)$ and $g(\sigma ^n)$ when $N>\beta (1-\alpha )$. Figure 6 shows $f(\sigma ^n)$ and $g(\sigma ^n)$ when $N<\beta (1-\alpha )$. Depending on the magnitude of $\eta$, there are two cases: (a) and (b). Panels (a) and (b) of Figs. 5 and 6 show that there exists a unique symmetric linear NNE, $\sigma ^{n*}>0$ if $A^{-\psi }>\delta$.

Fig. 5

Determination of $\sigma ^n$ when $N>\beta (1-\alpha )$

Fig. 6

Determination of $\sigma ^n$ when $N<\beta (1-\alpha )$

Fig. 7

Determination of $\sigma ^c$

1.2 B. Proof of Proposition 2

$0<\sigma ^c<A/N$ must be satisfied because $k^{\prime }=(A-N\sigma ^c)k>0$. We denote the left (right)-hand side of (24) as $q(\sigma ^c)$ ($m(\sigma ^c)$). Differentiating $q(x^c)$ with respect to $\sigma ^c$ leads to

$$\begin{aligned} q^\prime (\sigma ^c) =N (\psi -1) (A- N \sigma ^c)^{-\psi }<0. \end{aligned}$$

Note that $\psi <1$. Differentiating $q^\prime (\sigma ^c)$ with respect to $\sigma ^c$ results in

$$\begin{aligned} q^{\prime \prime }(\sigma ^c) =N^2 \psi (\psi -1) (A- N \sigma ^c)^{-\psi -1} {\left\{ \begin{array}{ll}>0 &{} \text {when }0<\eta<1, \\ <0 &{} \text {when }\eta >1. \end{array}\right. } \end{aligned}$$

Note that when $0<\eta <1$, $\psi <0$ holds. On the other hand, when $\eta >1$, $0<\psi <1$ holds. Moreover, $q(0)=A^{1-\psi }$ and $q(A/N)=0$ hold. The graph of $m(\sigma ^c)$ is a straight line:

$$\begin{aligned} m^\prime (\sigma ^c) = -(1-\beta )\delta N<0. \end{aligned}$$

(B1)

Moreover, $m(0)=A\delta$ and $m(A/N(1-\beta ))=0$ hold. Note that when $0<\beta <1$, $A/N(1-\beta )>A/N$ holds. From these results, we can graphically examine the existence of the CE. Figure 7 shows $q(\sigma ^c)$ and $m(\sigma ^c)$. Depending on the magnitude of $\eta$, there are two cases: (a) and (b). Panels (a) and (b) of Fig. 7 show that there exists a unique symmetric linear CE, $\sigma ^{c*}>0$, if $A^{-\psi }>\delta$.

1.3 C. Proof of Proposition 3

Note that $g(\sigma ^n)$ ($m(\sigma ^c)$) is the right-hand side of (14) ((24)). We first show that the two growth rates coincide when $N = 1-\alpha$. When $N=1-\alpha$, equation (14) is clearly equivalent to (24). Thus, $\sigma ^{n*}=\sigma ^{c*}$, that is, the two growth rates coincide.

We next examine the following two cases: (1) $N>1-\alpha$ and (2) $N<1-\alpha$.

Fig. 8

The relationship between $\sigma ^{n*}$ and $\sigma ^{c*}$ when $N>1-\alpha$

1.3.1 $(1)\ N>1-\alpha$

When $N>1-\alpha$, $N>\beta (1-\alpha )$ must hold. From (A1) and (B1), the graphs of $g(\sigma ^n)$ and $m(\sigma ^c)$ are the downward-sloping straight lines. We also obtain

$$\begin{aligned} -\{ N-\beta (1-\alpha )\}\delta<-(1-\beta )\delta N<0. \end{aligned}$$

Moreover, $g(0)=m(0)=A\delta$ holds. Therefore the graph of $m(\sigma ^c)$ is above that of $g(\sigma ^n)$. From these results, we can graphically examine the relationship between the two rates of consumption, $\sigma ^{n*}$ and $\sigma ^{c*}$ as in Fig. 8. Depending on the magnitude of $\eta$, there are two cases: (a) and (b). Panels (a) and (b) of Fig. 8 show that when $N>1-\alpha$,

$$\begin{aligned} \sigma ^{c*}<\sigma ^{n*}, \end{aligned}$$

which means that $G^c> G^n$.

1.3.2 $(2)\ N<1-\alpha$

We must distinguish the following two cases: (2-1) $N<\beta (1-\alpha )\ (<1-\alpha )$ and (2-2) $\beta (1-\alpha )<N\ (<1-\alpha )$.

Fig. 9

The relationship between $\sigma ^{n*}$ and $\sigma ^{c*}$ when $N<\beta (1-\alpha )\ (<1-\alpha )$

1.3.3 $(2-1)\ N<\beta (1-\alpha )\ (<1-\alpha )$

From (A1) and (B1), the graph of $g(\sigma ^n)$ is the upward-sloping straight line and the graph of $m(\sigma ^c)$ is the downward-sloping straight line. We can graphically examine the relationship between the two rates of consumption, $\sigma ^{n*}$ and $\sigma ^{c*}$ (Fig. 9). Depending on the magnitude of $\eta$, there are two cases: (a) and (b). Panels (a) and (b) of Fig. 9 show that when $N<\beta (1-\alpha )$,

$$\begin{aligned} \sigma ^{n*}<\sigma ^{c*}, \end{aligned}$$

which means that $G^c< G^n$.

1.3.4 $(2-2)\ \beta (1-\alpha )<N \ (<1-\alpha )$

The graphs of $g(\sigma ^n)$ and $m(\sigma ^c)$ are the downward-sloping straight lines. Contrary to the case of (1) $N>1-\alpha$, from (A1) and (B1), we obtain

$$\begin{aligned} 0>-\{ N-\beta (1-\alpha )\}\delta >-(1-\beta )\delta N. \end{aligned}$$

Thus, the graph of $m(\sigma ^c)$ is below that of $g(\sigma ^n)$. We can graphically examine the relationship between the two rates of consumption, $\sigma ^{n*}$ and $\sigma ^{c*}$ (Fig. 10). Depending on the magnitude of $\eta$, there are two cases: (a) and (b). Panels (a) and (b) of Fig. 10 show that when $\beta (1-\alpha ) <N$,

$$\begin{aligned} \sigma ^{n*}<\sigma ^{c*}, \end{aligned}$$

which means that $G^c< G^n$.

Fig. 10

The relationship between $\sigma ^{n*}$ and $\sigma ^{c*}$ when $\beta (1-\alpha )<N \ (<1-\alpha )$

Fig. 11

The effect of a decrease in $\beta$ on $\sigma ^n$ when $N>\beta (1-\alpha )$

Fig. 12

The effect of a decrease in $\beta$ on $\sigma ^n$ when $N<\beta (1-\alpha )$

Fig. 13

The effect of a decrease in $\beta$ on $\sigma ^c$

1.4 D. Proof of Lemma 1

Note that $f(\sigma ^n)$ ($q(\sigma ^c)$) is the left-hand side of (14) ((24)) and $g(\sigma ^n)$ ($m(\sigma ^c)$) is the right-hand side of (14) ((24)). We show that a decrease in $\beta$ reduces the growth rates $G^n$ and $G^c$. From (14) and (24), the partial derivatives of $g(\sigma ^n)$ and $m(\sigma ^c)$ with respect to $\beta$ are as follows:

$$\begin{aligned} \frac{\partial g}{\partial \beta }&= (1-\alpha )\delta \sigma ^n>0, \\ \frac{\partial m}{\partial \beta }&= \delta N \sigma ^c>0. \end{aligned}$$

This shows that a decrease in $\beta$ shifts the graphs of $g(\sigma ^n)$ and $m(\sigma ^c)$ downward. Moreover, $\beta$ does not affect $f(\sigma ^n)$ and $q(\sigma ^c)$. Thus, we can draw Figs. 11, 12 and 13. Figure 11 shows the effect of a decrease in $\beta$ on $\sigma ^n$ when $N>\beta (1-\alpha )$. Figure 12 shows the effect of a decrease in $\beta$ on $\sigma ^n$ when $N<\beta (1-\alpha )$. Figure 13 shows the effect of a decrease in $\beta$ on $\sigma ^c$. Depending on the magnitude of $\eta$, there are two cases: (a) and (b). Panels (a) and (b) of Figs. 11, 12 and 13 show that decreases in $\beta$ increase $\sigma ^{n*}$ and $\sigma ^{c*}$, which means that decreases in $\beta$ decrease the growth rates, $G^n$ and $G^c$.

1.5 E. Derivation of (27)

If each consumption is symmetric and constant over time, we can calculate the utility of the individuals in period t as follows:

$$\begin{aligned} U_{t}&=\frac{\eta }{\eta -1}(\sigma ^{i} k_t \cdot (\sigma ^{i} k_t)^{-\alpha })^{1-\frac{1}{\eta }}+\beta \sum _{j=1}^{\infty } \delta ^j \frac{\eta }{\eta -1}(\sigma ^{i} k_{t+j} \cdot (\sigma ^{i} k_{t+j})^{-\alpha })^{1-\frac{1}{\eta }}\\&= \frac{\eta }{\eta -1} \left[ (\sigma ^{i} k_t)^{\psi }+\beta \delta (\sigma ^{i} k_{t+1})^{\psi }+\beta \delta ^2(\sigma ^{i} k_{t+2})^{\psi }+ \cdots \right] \\&= \frac{\eta }{\eta -1} (\sigma ^{i} k_t)^{\psi }\left[ 1+\beta \delta (A-N\sigma ^{i})^{\psi }+\beta \delta ^2(A-N\sigma ^{i})^{2\psi } \cdots \right] . \end{aligned}$$

The third equality holds because of $k_{j+1}=(A-N\sigma ^{i})k_{j}$, $j=0,1,2, \cdots$. We assume that $0<\delta (A-N\sigma ^{i})^{\psi }<1$ to guarantee the finiteness of the welfare level. We can rewrite the above utility as follows:

$$\begin{aligned} U_t&= \frac{\eta }{\eta -1}(\sigma ^{i} k_t)^{\psi }\left[ 1+\frac{\beta \delta (A-N\sigma ^{i})^{\psi }}{1-\delta (A-N\sigma ^{i})^{\psi }} \right] \\&= W^i(k_t). \end{aligned}$$

1.6 F. Derivation of (28)

From (27) and $k_{j+1}=(A-N\sigma ^{i})k_{j}$, $j=0,1,2, \cdots$, we can calculate

$$\begin{aligned} W^i(k_t)&=(A-N\sigma ^{i})^{\psi }\frac{\eta }{\eta -1}(\sigma ^{i} k_{t-1})^{\psi }\left[ 1+\frac{\beta \delta (A-N\sigma ^{i})^{\psi }}{1-\delta (A-N\sigma ^{i})^{\psi }} \right] \\&= (A-N\sigma ^{i})^{\psi } W^i(k_{t-1}) \\&= (A-N\sigma ^{i})^{2\psi } W^i(k_{t-2}) \\&= \cdots \\&=[(A-N\sigma ^{i})^{\psi }]^t W^i(k_0). \end{aligned}$$

1.7 G. Proof of the uniqueness of $\sigma ^{*}$

From (27), differentiating $W(k_0)$ with respect to $\sigma$ leads to

$$\begin{aligned} \frac{d W(k_0)}{d \sigma }= & {} \frac{(1-\alpha )(k_0)^{\psi }(\sigma )^{\psi -1}}{\{1-\delta (A-N\sigma )^{\psi }\}^2} \left[ 1+(1-\beta )\delta (A-N\sigma )^{\psi }\{ \delta (A-N\sigma )^{\psi }-2\}\nonumber \right. \\&\left. -\beta \delta A(A-N\sigma )^{\psi -1} \right] . \end{aligned}$$

From (3), (25), and (26), $G \equiv A-N\sigma$. Let us define $L(G ) \equiv 1+(1-\beta )\delta (G )^{\psi }\{ \delta (G )^{\psi }-2\}$ and $R(G ) \equiv \beta \delta A(G )^{\psi -1}$. Differentiating L(G) and R(G) with respect to G results in

$$\begin{aligned} L^\prime (G )&\equiv 2\psi (1-\beta )\delta (G )^{\psi -1}\{ \delta (G )^{\psi }-1\} {\left\{ \begin{array}{ll}>0 &{} \text {when }0<G<\delta ^{-\frac{1}{\psi }}, \\<0 &{} \text {when }G >\delta ^{-\frac{1}{\psi }}, \end{array}\right. } \\ R^\prime (G )&\equiv -\beta \delta A(1-\psi )(G )^{\psi -2}<0. \end{aligned}$$

Since $(1-\alpha )>0$, $k_0>0$, and $\sigma >0$, we obtain

$$\begin{aligned} \text {sign}\ \left[ \frac{d W(k_0)}{d \sigma } \right] = \text {sign}\ \left[ L(G )-R(G ) \right] . \end{aligned}$$

Therefore, the uniqueness of $\sigma ^{*}$ is guaranteed if there is a unique ${\widehat{G}}$ that satisfies $L({\widehat{G}})=R({\widehat{G}})$ and maximizes $W(k_0)$. We examine how G affects $L(G )-R(G )$. We must distinguish between the following two cases: $0<\psi <1$ and $\psi <0$.

1.7.1 (1) $0<\psi <1$

We first examine the feasible interval of G. Since $\sigma >0$ and $G>0$, $0<G<A$ must hold. From Appendix E, we assume that $0<\delta (G )^{\psi }<1$, which means that $0<G <\delta ^{-\frac{1}{\psi }}$. Moreover, from Propositions 1 and 2, $A^{-\psi }>\delta$ must hold for the existence of a unique equilibrium. Thus, $A<\delta ^{-\frac{1}{\psi }}$. Therefore, the feasible interval of G is $0<G <A$.

We next examine the difference $L(G )-R(G )$. Since $L(0)=1$ and $\lim _{G \rightarrow 0} R(G )=+ \infty$, we obtain $\lim _{G \rightarrow 0} L(G )-R(G )<0$. When $G =A$, we obtain $L(A)-R(A) =(1-\beta )[\delta (A)^{\psi }]^2-(2-\beta )\delta (A)^{\psi }+1$. From Propositions 1 and 2, $A^{-\psi }>\delta$ must hold. Thus, $0<\delta (A)^{\psi }<1$. Let us define $\Omega \equiv \delta (A)^{\psi }$ and $Z(\Omega )\equiv (1-\beta )\Omega ^2-(2-\beta )\Omega +1$. $Z(\Omega )>0$ holds because $Z(0)=1>0$, $Z(1)=0$, and $Z^\prime (\Omega )=2(1-\beta )\Omega -(2-\beta )<0$ for all $\Omega \in (0, 1)$ and $\beta \in (0, 1)$. This result implies that $L(A)-R(A)>0$. Since L(G) and R(G) are decreasing in G when $0<G <A$, the sufficient condition for the existence of ${\widehat{G}}$ is $L^\prime (G )>R^\prime (G )$ for all $G \in (0, A)$. $L^\prime (G )-R^\prime (G )$ results in

$$\begin{aligned} L^\prime (G )-R^\prime (G )&= [ 2(1-\beta )\psi \{ \delta (G )^{\psi }-1\}G +\beta A(1-\psi )]\delta (G )^{\psi -2}\\&> [-2(1-\beta )\psi G +\beta A(1-\psi )]\delta (G )^{\psi -2}\\&>[-2(1-\beta )\psi A+\beta A(1-\psi )]\delta (G )^{\psi -2}\\&= [\beta (1+\psi )-2\psi ]A\delta (G )^{\psi -2}. \end{aligned}$$

Therefore, if $\beta \ge 2\psi /1+\psi$ holds, $L^\prime (G )-R^\prime (G )>0$ holds for all $G \in (0, A)$. This result shows that the uniqueness of $\sigma ^{*}$ is guaranteed when $0<\psi <1$. Note that if $\beta =1$, the uniqueness of $\sigma ^{*}$ is always guaranteed.

1.7.2 (2) $\psi <0$

We first examine the feasible interval of G. Since $\sigma >0$ and $G >0$, $0<G <A$ must hold. From Appendix E, we assume that $0<\delta (G )^{\psi }<1$. Thus, $G >\delta ^{-\frac{1}{\psi }}$. Moreover, from Propositions 1 and 2, $A^{-\psi }>\delta$ must hold for the existence of a unique equilibrium. This property implies that $A>\delta ^{-\frac{1}{\psi }}$. Therefore, the feasible interval of G is $\delta ^{-\frac{1}{\psi }}<G <A$.

We next examine $L(G )-R(G )$. As in the case of $0<\psi <1$, we obtain $L(A)-R(A)>0$. Since $A^{-\psi }>\delta$ means that $A\delta ^{\frac{1}{\psi }}>1$, $L(\delta ^{-\frac{1}{\psi }})-R(\delta ^{-\frac{1}{\psi }})=\beta (1-A\delta ^{\frac{1}{\psi }})<0$ holds. Moreover, when $\delta ^{-\frac{1}{\psi }}<G <A$, the graph of L(G) is upward sloping and the graph of R(G) is downward sloping. Therefore, when $\psi <0$ and $\delta ^{-\frac{1}{\psi }}<G <A$, there always exists a unique ${\widehat{G}}$ that satisfies $L({\widehat{G}})=R({\widehat{G}})$. Note that if $\beta =1$, the uniqueness of $\sigma ^{*}$ is also always guaranteed.