Informal property rights as stable conventions in hawk-dove games with many players

Abstract

This paper investigates the evolution of conventions (Young Econometrica 61(1):57–84, 1993) in n-player hawk-dove games where multiple players share the same payoff-irrelevant label, such as “blue” or “green”. With more than two players, the stochastically stable equilibrium depends on how many players in the contest share each label. If the cost of fighting is high, then the long-run equilibrium is favorable to the label shared by fewer players – those players play hawk – while if the cost is low, then the opposite convention develops. This result provides one explanation for the emergence of informal property rights. In disputes over property, a fundamental distinction exists between the possessor, who is unique, and non-possessors, who can be several. For objects whose value is low relative to the cost of conflict over them, this asymmetry favors the development of informal property rights conventions.

Appendices

Appendix A: Proofs

The following arguments can be trivially extended to hold for n _y > 1 provided that n _y < n _x + 1; the main difficulty is that asymmetric Nash equilibria may involve mixing by both roles in additional cases. For instance, if c > 1 and n _y = 2 < n _x = 4, the y-aggressive equilibrium has h _y (ω _y ) < 1. See the working paper version of the paper for details.

Some additional notation is used throughout the proofs. Let

$$ d(z)\equiv \mathrm{E}\left[u_{i}(a_{i}=H;a_{-i})-u_{i}(a_{i}=D;a_{-i}) \mid z = \sum\limits_{i=1}^{n}{\mathbf{1}_{(a_{i}=H)}}\right] $$

(5)

denote the payoff difference between a = H and a = D when there are z hawks. Let

$$ d_{r}(h_{r},h_{-r})\equiv \mathrm{E}\left[u_{r}(H)-u_{r}(D)|h_{r},h_{-r}\right] $$

(6)

be the expected difference in utility for an r-player between a = H and a = D when r’s and −r’s play a = H with frequency h _r and h _−r , respectively. Finally, in a slight abuse of notation, I use m = h _x (θ _m ) = h _y (θ _m ) to refer throughout to the fraction of hawks in the totally mixed equilibrium.

1.1 A.1 Proof of Theorem 1

Clearly there exists an m such that d _x (m, m) = d _y (m, m) (equilibrium (i)). Now consider the asymmetric case. The maximum number of hawk players such that the hawk players are best responding to each other, if all other players play dove, is $\lceil \frac {1}{c} \rceil = \max ~\{z \mid d(z)>0\}$. If $\lceil \frac {1}{c} \rceil > n_{r}$, then there is an h _−r ∈ (0, 1) where d _r (1, h _−r ) ≥ 0 and d _−r (h _−r ,1) = 0 (equilibrium (ii)). Likewise, if $\lceil \frac {1}{c} \rceil \leq n_{r}$, there is an h _r such that d _r (h _r , 0) ≥ 0 and d _s (0, h _r ) < 0 (equilibrium (iii)).

Finally, consider h _x ≠ h _y and assume towards contradiction that h _x , h _y ∈ (0, 1) and d _x (h _x , h _y ) = d _y (h _y , h _x ) = 0. Because n _x ≠ n _y and both roles are mixing, an x-player faces a different distribution of hawks than a y-player, so it cannot be the case that d _x (h _x , h _y ) = d _y (h _y , h _x ). Thus no other equilibria exist.

1.2 A.2 Proof of Lemma 1

Limit points (i and ii)

For θ to be a limit point, it must be the case that for all every player i, for both roles r,

$$ s_{r}(i,\theta) = a \Rightarrow s_{r}^{\ast}(i,\theta) =a, $$

(7)

i.e., every player’s strategy must be a best-response to the population minus herself.

Consider ω _x where $\lfloor h^{\ast }_{x} K \rfloor$ players have s _x (i, ω _x ) = H, s _y (i, ω _x ) = D and $h_{x}^{\ast }$ is the fraction of x-hawks in the x-aggressive equilibrium and all other plays play D always (ω _y is similar and omitted).¹² All players have $s_{y}(i,\theta ) = s_{y}^{\ast }(i,\theta ) = D$, so the y-component of their strategies is a best response to the rest of the population. If s _x (i, ω _x ) = H, player i has $\hat h_{x}(i,\omega _{x}) = (K h_{x}(\omega _{x}) -1)/(K-1) < h_{x}^{\ast }$, and so $s_{x}^{\ast }(i,\omega _{x}) = H$. Alternatively, if s _x (i, ω _x ) = D, player i has $\hat h_{x}(i,\omega _{x}) = (K h_{x}(\omega _{x}))/(K-1) > h_{x}^{\ast }$, and so $s_{x}^{\ast }(i,\omega _{x}) = D$.

Now consider ω _m where this limit point is the state in which ⌊m K⌋ players have s _x (i, ω _m ) = s _y (i, ω _m ) = H and the remainder always play D. In ω _m , hawk players face $\hat h_{x}(i,\omega _{m}) = \hat h_{y}(i,\omega _{m}) = (K h_{x}(\omega _{m}) - 1)/(K-1) < m$ so for these players $s_{x}^{\ast }(i,\omega _{m}) = s_{y}^{\ast }(i,\omega _{m}) = H$. Dove players similarly best respond by playing dove independent of role. Finally, any point θ with h(θ) close to (m, m) but θ ≠ ω _m cannot be a limit point. In all of these θ, it must be the case that at least one player has s _x (i, θ) = D ≠ s _y (i, θ) = H. That player has $s_{y}^{\ast }(i,\theta ) = D$, violating (7).

Diagonal basin of ω _m (i)

No state θ with h _x (θ) = h _y (θ) in which all players’ strategies are independent of their roles can transition off the diagonal without errors. $\hat h_{x}(i,\theta ) = \hat h_{y}(i,\theta )$, so either $s_{x}^{\ast }(i,\theta ) = s_{y}^{\ast }(i,\theta ) = H$ or $s_{x}^{\ast }(i,\theta ) = s_{y}^{\ast }(i,\theta ) = D$. Furthermore, transitions move the state toward ω _m .

Rectangular basins of ω _x and ω _y (ii)

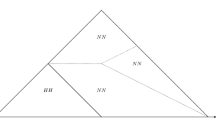
Consider without loss of generality B(ω _x ). The rectangular region R _x = {θ∣θ ∈ Θ, h _x (θ) > m > h _y (θ)} is depicted in Fig. 7. For any player i, in the area labeled A for either r, $s^{\ast }_{r}(i,\theta ) = H$; in the area labeled B, $s^{\ast }_{x}(i,\theta ) = H$, and $s^{\ast }_{y}(i,\theta ) = D$; and in the area labeled C, for either r, $s^{\ast }_{r}(i,\theta ) = D$.¹³ Depending on the current strategy of an updating player i, if θ _t ∈ B it can be the case that either h _x increases (if s _i = D D), h _y decreases (if s _i = H H), or both changes occur (if s _i = D H). These possibilities imply that if θ _t ∈ B then $\theta _{t+1} \in B \cup C$. Now if θ _t ∈ C, h _x can decrease, h _y can decrease, or both. It may be the case that near the interior corner of R _x , a decrease in h _x holding h _y constant could lead to θ _{t + 1} ∈ A if θ _t ∈ C, because states are on a grid in h-space and there be no point between A and C which is in B. However, if $h_{y} < \max \{ h_{y}(\theta ) \mid \theta \in {\Theta }_{1} \land \forall i, s_{x}^{\ast }(i,\theta ) = H \land s_{y}^{\ast }(i,\theta ) = D\}$ then for every θ ∈ C there is eventually a θ ∈ B to its left. Therefore the set of states in R _x satisfying this condition are never exited under the unperturbed dynamic, and in $B\cup C$, ω _x is eventually reached.

Fig. 7

B(ω _x )

Square non-basins (iii)

Without loss of generality consider a point with x < h _x (θ _m ) and y < h _y (θ _m ). Let θ satisfy h(θ) = (x, y) and let θ consist of at least one player that uses strategy DH and at least one player that plays HD. Then B(ω _y ) can be reached by all players who play HD updating to HH, after which h _y (θ) > h _x (θ), and if necessary enough DD players then updating to lead to h _y (θ) > m. Alternatively, B(ω _x ) can be reached if instead of HD players updating, DH players update, after which h _x (θ) > h _y (θ).¹⁴

Cost (iv)

It requires one error to move distance 1/K either diagonally (HH to DD or vice-versa), vertically (HD to HH or DD to DH or vica-versa), or horizontally (HD to DD or HH to DH or vice-versa) in h-space. By exploiting diagonal movement to the maximum extent possible, the cost can reduced to approximately proportional to the $L_{\infty }$ distance in h-space.

1.3 A.3 Proof of Lemma 2

For z ≥ 1, d(z) as defined in Eq. 5 is strictly decreasing and strictly convex in z when n ≥ 3 and c > 1/n. Let F be the cumulative distribution function for w and $F^{\prime }$ be the cumulative distribution function for $w^{\prime }$. $F^{\prime }$ is a mean-preserving spread of F, and so F second-order stochastically dominates $F^{\prime }$. Therefore (c.f. Mas-Collell et al. (1995, Proposition 6.D.2)) $d_{x}(h_{x}^{\prime },h_{y}^{\prime })>d_{x}(h_{x},h_{y})$, as claimed.

1.4 A.4 Proof of Theorem 2

Notation

Let ${E^{i}_{j}}$ denote the distance necessary to leave ω _i through errors that reduce strategy component j, so for example $E^{x}_{xh}$ is the distance necessary to leave ω _x by players switching from a strategy of hawk when x to dove when x, and $E^{x}_{xh} \equiv h_{x}(\omega _{x})-h_{x}(\theta _{m})$. From Lemma 1, claims (ii) to (iv) imply that for large K, $\mathrm {R}(\omega _{x}) \propto \min \{E^{x}_{xh},\,E^{x}_{yd}\}$ and $\mathrm {R}(\omega _{y})\propto \min \{E^{y}_{yh},\,E^{y}_{xd}\}$.¹⁵ See Fig. 8.

Fig. 8

(h _x , h _y ) State Space and Notation in Theorem 2 and Theorem B1. $R(\omega _{x}) \propto \min \{E^{x}_{xh},~E^{x}_{yd}\}$ and $R(\omega _{y})\propto \min \{E^{y}_{yh},~E^{y}_{xd}\}$

Proof for case in which h _x (ω _y ) = 0

First, n _x > n _y implies $\mathrm {R}(\omega _{x}) = E^{x}_{xh}$: from Lemma 2, at a point $(\overline {x}_{0},0)$ that is a mean-hawk-preserving contraction in the distribution of hawks for x-players at (m, m), dove is the best response for them. From its definition $\overline {x}_{0}= m \left (\frac {n-1}{n_{x}-1} \right )$. Therefore,

$$E^{x}_{xh} < \overline{x}_{0} - m = m \left( \frac{n-1}{n_{x}-1}\right) - m = m \left( \frac{n_{y}}{n_{x} - 1} \right) \leq m =E^{x}_{yd}, $$

and so $\mathrm {R}(\omega _{x}) \propto E^{x}_{xh}$.

Second, both $E^{y}_{yh}$ and $E^{y}_{xd}$ are greater than $E^{x}_{xh}$, implying R(ω _y ) > R(ω _x ) = CR(ω _y ): Because h _y (ω _y ) = 1 > h _x (ω _x ), comparing the reflection of $E^{y}_{yh}$ to $E^{x}_{xh}$, $E^{y}_{yh} > E^{x}_{xh}$. Turning to $E^{y}_{xd}$, reflecting $E^{y}_{xd}$ across the 45^∘ line shows that it the same length as $E^{x}_{yd}$, so $E^{y}_{xd} = m=E^{x}_{yd} > E^{x}_{xh}$.

Proof for case in which h _y (ω _x ) = 0

First, note that like above $E^{x}_{xh} < E^{x}_{yd}$. Second, because h(ω _x ) = (1,0), the line segment $E^{x}_{xh}$ is a reflection of and equal in length to the line segment $E^{y}_{yh}$, so $E^{x}_{xh}=E^{y}_{yh}$.

Now consider $E^{y}_{yh}$ and $E^{y}_{xd}$. h(ω _y ) is defined by the intersection of the line h _y = 1 and d _x (h _x , h _y ) = 0, the indifference curve for x-players. Let H _x be the CDF for the distribution of other hawks faced by an x-player at h = (h _x , h _y ) and $H_{x}^{\prime }$ be the CDF for $h^{\prime }=(h_{x}-\delta ,h_{y}+\delta )$ (for small δ). Because an x-player plays against more x-players than y-players (n _y < n _x − 1), H _x first-order stochastically dominates $H_{x}^{\prime }$. Therefore because d(⋅) in Eq. 5 is strictly convex, $d_{x}(h_{x},h_{y})<d_{x}(h_{x}^{\prime },h_{y}^{\prime })$ (Mas-Colell et al. 1995, Proposition 6.D.1). Thus the curve d _x (h _x , h _y ) = 0 must be steeper than 45^∘, which implies $R(\omega _{y}) = E^{y}_{xd}<E^{y}_{yh}=E^{x}_{xh}=R(\omega _{x})$.

1.5 A.5 Proof of Theorem 3

Consider shifts from ω _m to either (x ₀,0) or (x ₁,1) that preserve the expected number of hawks an x-player faces, so x ₀ = (1/2)n _x /(n _x − 1) and x ₁ = (1/2)(n _x − 2)/(n _x − 1). Then using Lemma 2, h _x (ω _x ) < x ₀ and h _x (ω _y ) < x ₁. Because $E^{y}_{yh}=E^{x}_{yd}=1/2$ and both $E^{y}_{xd}$ and $E^{x}_{xh}$ are less than 1/2, R(ω _x ) = h _x (ω _x )−1/2 and R(ω _y ) = 1/2−h _x (ω _y ). From the upper bounds on h _x (ω _r ), it follows that CR(ω _y ) = R(ω _x ) < (1/2)/(n _x − 1) < R(ω _y ), implying that ω _y is uniquely stochastically stable.

Appendix B: Alternative assumptions about the state space

In addition to the one population state space assumption in the body, other assumptions about the underlying population turn out to produce similar long-run equilibrium predictions. A particular alternate assumption is that there are two distinct populations from which players for each role are drawn. This section defines this state space, Θ₂, shows that my results continue to hold under it, and finally discusses other variants of the state space.

Depending on the situation being modeled, either Θ₁ or Θ₂ might be appropriate. If informal property rights norms apply to a variety of objects, so that everyone is simultaneously a possessor (of some kinds of objects) and a non-possessor (of others), then that environment is like Θ₁, in that each player’s choice in both roles is important. Alternatively, only one kind of object, such as housing, might be subject to informal property rights. That would be more akin to two separate populations of players, one possessing housing and the other not possessing housing, so Θ₂ is more reflective of that environment.

Under Θ₂, there is a distinct x-population and y-population, of size K _x and K _y respectively. Each player has a strategy s ∈ A. Every round as many groups of (n _x +n _y ) players as possible are formed by drawing n _x players from the x-population and n _y players from the y-population. These groups of players then each play a n-player hawk-dove game. Within a population any player is equally likely to be drawn for the contest. At the end of the period, one player is selected with equal probability from the set of all players to reevaluate her strategy.

Definition 5

A two population state space is represented by ${\Theta }_{2} = \{\theta \mid \theta \in \mathbb {N}^{2} ,~ \theta _{i}\leq K_{i}\}$, where each dimension indicates the number of players in a particular population playing hawk.

Unlike Θ₁, θ ∈ Θ₂ do correspond 1:1 with points in (h _x , h _y )-space. This means that the geometric comparisons for Θ₁ apply to Θ₂ with K _x = K _y as well.¹⁶ If K _x > K _y , however, an error by an x-player will shift h _x by a smaller amount than an error by a y-player would shift h _y . This tends to magnify the importance of errors by the smaller population. Nonetheless, the basic message of Theorem 3 still holds with population size disparities:

Theorem B1

In hawk-dove games with behavior evolving according to asynchronous perturbed best-response dynamics on a Θ ₂ state space, if the fraction of hawks in the totally mixed equilibrium is m < 1/2, and either

• i) K _y ≪ K _x and n _y ≤n _x , or

• ii) K _y ≫ K _x and n _y < n _x ,

then the y-aggressive equilibrium is the unique stochastically stable equilibrium.

Theorem B1 (whose proof is below) shows that noisy evolution favors y-aggressive equilibria if c is high enough (so that m < 1/2) for Θ₂ with large differences in population size.¹⁷ Theorem B1’s result also applies to evolution in two-player hawk-dove games if the x-population greatly outnumbers the y-population. In that case the disparity between K _x and K _y alone is enough to favor y’s.

Finally, a third plausible alternative for the state space would be to have particular players possess both a role and a (possibly role-contingent) strategy. For instance, a hawk who was an x-player might transform into a y-player upon winning. If transformations of winning x-players into y-players occured, that would tend to make movements from ω _x less costly, so my main results would continue to go through. However, this possibility has already been addressed by Gintis (2007) and Kokko et al. (2006), among others, and so I do not model it formally.

1.1 B.1 Proof of Theorem B1

Let κ = K _x /K _y . Using the notation of Theorem 2,

$$\begin{array}{@{}rcl@{}} \mathrm{R}(\omega_{x}) & \propto & \min~\{K_{x} E^{x}_{xh},~K_{y} E^{x}_{yd}\} = \min~\{\kappa E^{x}_{xh},~ E^{x}_{yd}\} \\ \mathrm{R}(\omega_{y}) & \propto & \min~\{K_{x} E^{y}_{xd},~K_{y} E^{y}_{yh}\} = \min~\{\kappa E^{y}_{xd},~E^{y}_{yh}\} \end{array} $$

For K _y ≪ K _x ,

$$\lim\limits_{\kappa \rightarrow \infty}{\mathrm{R}(\omega_{x})}=E^{x}_{yd}=m \qquad \text{and} \qquad \lim\limits_{\kappa \rightarrow\infty}{\mathrm{R}(\omega_{y})}=E^{y}_{yh}=1-m. $$

Hence R(ω _y ) > R(ω _x ) if and only if m < 1/2. For K _y ≫ K _x ,

$$\lim\limits_{\kappa \rightarrow 0}{\mathrm{R}(\omega_{x})}=E^{x}_{xh} \qquad \text{and} \qquad \lim\limits_{\kappa \rightarrow 0}{\mathrm{R}(\omega_{y})}=E^{y}_{xd} . $$

$E^{x}_{xh} < E^{y}_{xd}$ follows from parallel arguments to those of Theorem 2.