Skip to main content
SpringerLink
Log in

Five-axis flank milling stability prediction by considering the tool-workpiece interactions and speed effect

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

A Correction to this article was published on 06 June 2020

This article has been updated

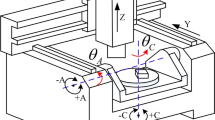
Abstract

Chatter is one of the challenging topics in the field of metal cutting. The dynamic characteristics of five-axis milling system are complex and variable. Especially in high-speed milling process, the influence of the tool-workpiece interactions and speed effect on milling stability is more obvious. It is necessary to investigate the influence of various interaction effects on milling stability. In this paper, the dynamical model of spindle system was established, and then the model was applied to investigate the influence of gyroscopic effect and centrifugal force on the dynamical characteristics of the tool tip. In order to solve the chatter problem of five-axis flank milling, the extended dynamical model of five-axis flank milling which considers the tool-workpiece interactions and speed effect was established. Based on the established milling dynamical model, the influence mechanism of the spindle system-tool-workpiece interaction effects on five-axis flank milling stability was investigated. The stability lobe diagrams of five-axis flank milling which contains the tool-workpiece interactions and speed effect can be obtained. Experimental results show that the proposed five-axis flank milling dynamical model can predict the milling state more reliable than the traditional ones. The research results are of great significance in preventing five-axis flank milling chatter.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26

Similar content being viewed by others

Change history

  • 06 June 2020

    This original article contained a mistake.

References

  1. Yue CX, Gao HN, Liu XL, Liang SY, Wang LH (2019) A review of chatter vibration research in milling. Chin J Aeronaut 32(2):215–242

    Article  Google Scholar 

  2. Altintas Y, Weck M (2004) Chatter stability of metal cutting and grinding. CIRP Ann-Manuf Technol 53(2):619–642

    Article  Google Scholar 

  3. Sun T, Qin LF, Fu YC, Hong JM (2019) Chatter stability of orthogonal turn-milling analyzed by complete discretization method. Precis Eng 56:87–95

    Article  Google Scholar 

  4. Munoa J, Beudaert X, Dombovari Z, Altintas Y, Budak E, Brecher C, Stepan G (2016) Chatter suppression techniques in metal cutting. CIRP Ann-Manuf Technol 65:785–808

    Article  Google Scholar 

  5. Quintana G, Ciurana J (2011) Chatter in machining processes: a review. Int J Mach Tools Manuf 51(5):363–376

    Article  Google Scholar 

  6. Altintas Y, Budak E (1995) Analytical prediction of stability lobes in milling. CIRP Ann-Manuf Technol 44(1):357–362

    Article  Google Scholar 

  7. Budak E, Altintas Y (1998) Analytical prediction of chatter stability in milling—part I: general formulation. J Dyn Syst Meas Control 120(1):22–30

    Article  Google Scholar 

  8. Merdol SD, Altintas Y (2004) Multi frequency solution of chatter stability for low immersion milling. J Manuf Sci Eng-Trans ASME 126(3):459–466

    Article  Google Scholar 

  9. Zhu LD, Liu BG, Chen HY (2018) Research on chatter stability in milling and parameter optimization based on process damping. J Vib Control 24(12):2642–2655

    Article  Google Scholar 

  10. Ding Y, Zhu LM, Zhang XJ (2010) Ding H (2010) a full-discretization method for prediction of milling stability. Int J Mach Tools Manuf 50(5):502–509

    Article  Google Scholar 

  11. Zhou K, Feng PF, Xu C, Zhang JF, Wu ZJ (2017) High-order full-discretization methods for milling stability prediction by interpolating the delay term of time-delayed differential equations. Int J Adv Manuf Technol 93(5–8):2201–2214

    Article  Google Scholar 

  12. Ding Y, Zhu LM, Zhang XJ, Ding H (2011) Numerical integration method for prediction of milling stability. J Manuf Sci Eng-Trans ASME 133(3):1–9

    Article  Google Scholar 

  13. Zhang Z, Li HG, Meng G, Liu C (2015) A novel approach for the prediction of the milling stability based on the Simpson method. Int J Mach Tools Manuf 99:43–47

    Article  Google Scholar 

  14. Yan BL, Zhu LD (2019) Research on milling stability of thin-walled parts based on improved multi-frequency solution. Int J Adv Manuf Technol 102(1–4):431–441

    Article  Google Scholar 

  15. Ning JS, Zhu LD (2019) Parametric design and surface topography analysis of turbine blade processing by turn-milling based on CAM. Int J Adv Manuf Technol 104(9–12):3977–3990

    Article  Google Scholar 

  16. Dun YC, Zhu LD, Wang SH (2020) Multi-modal method for chatter stability prediction and control in milling of thin-walled workpiece. Appl Math Model 80:602–624

    Article  MathSciNet  MATH  Google Scholar 

  17. Liu CF, Zhu LD, Ni CB (2018) Chatter detection in milling process based on VMD and energy entropy. Mech Syst Signal Process 105:169–182

    Article  Google Scholar 

  18. Ahmadi K, Altintas Y (2014) Identification of machining process damping using output-only modal analysis. J Manuf Sci Eng-Trans ASME 136(5):1–13

    Article  Google Scholar 

  19. Tunc LT, Budak E (2013) Identification and modeling of process damping in milling. J Manuf Sci Eng-Trans ASME 135(2):1–12

    Article  Google Scholar 

  20. Gurdal O, Ozturk E, Sims ND (2016) Analysis of process damping in milling. Procedia CIRP 55:152–157

    Article  Google Scholar 

  21. Sisson TR, Kegg RL (1969) An explanation of low-speed chatter effects. J Eng Ind 91(4):951–958

    Article  Google Scholar 

  22. Peters J, Vanherck P, Brussel HV (1971) The measurement of the dynamic cutting coefficient. CIRP Ann-Manuf Technol 21(2):129–136

    Google Scholar 

  23. Tlusty J (1978) Analysis of the state of research in cutting dynamics. CIRP Ann-Manuf Technol 27(2):583–589

    Google Scholar 

  24. Tlusty J, Ismail F (1983) Special aspects of chatter in milling. J Vib Acoust Stress Reliab Des-T ASME 105(1):24–32

    Article  Google Scholar 

  25. Wu DW (1989) A new approach of formulating the transfer function for dynamic cutting process. J Eng Ind-Trans ASME 111(1):37–47

    Article  Google Scholar 

  26. Ahmadi K, Ismail F (2012) Stability lobes in milling including process damping and utilizing multi-frequency and semi-discretization methods. Int J Mach Tools Manuf 54-55:46–54

    Article  Google Scholar 

  27. Ahmadi K, Ismail F (2011) Analytical stability lobes including nonlinear process damping effect on machining chatter. Int J Mach Tools Manuf 51(4):296–308

    Article  Google Scholar 

  28. Wang DQ, Löser M, Ihlenfeldt S, Wang XB, Liu ZB (2019) Milling stability analysis with considering process damping and mode shapes of in-process thin-walled workpiece. Int J Mech Sci 159:382–397

    Article  Google Scholar 

  29. Wan M, Feng J, Ma YC, Zhang WH (2017) Identification of milling process damping using operational modal analysis. Int J Mach Tools Manuf 122:120–131

    Article  Google Scholar 

  30. Feng J, Wan M, Gao TQ, Zhang WH (2018) Mechanism of process damping in milling of thin-walled workpiece. Int J Mach Tools Manuf 134:1–19

    Article  Google Scholar 

  31. Zhang XJ, Xiong CH, Ding Y, Feng MJ, Xiong YL (2012) Milling stability analysis with simultaneously considering the structural mode coupling effect and regenerative effect. Int J Mach Tools Manuf 53(1):127–140

    Article  Google Scholar 

  32. Tang XW, Peng FY, Yan R, Gong YH, Li X (2016) An effective time domain model for milling stability prediction simultaneously considering multiple modes and cross-frequency response function effect. Int J Adv Manuf Technol 86(1–4):1037–1054

    Article  Google Scholar 

  33. Li ZY, Jiang SL, Sun YW (2019) Chatter stability and surface location error predictions in milling with mode coupling and process damping. Proc IMechE Part B: J Eng Manuf 233(3):686–698

    Article  Google Scholar 

  34. Ozturk E, Bilkhu R, Turner S (2012) A study on the effects of spindle speed on tool tip dynamics. The 15th International Conference on Machine Design and Production, Denizli

    Google Scholar 

  35. Zorzi ES, Nelson HD (1977) Finite element simulation of rotor-bearing systems with internal damping. J Eng Power 99(1):71–76

    Article  Google Scholar 

  36. Nelson HD (1980) A finite rotating shaft element using Timoshenko beam theory. J Mech Design 102:793–803

    Article  Google Scholar 

  37. Lin CW, Tu JF, Kamman J (2003) An integrated thermo-mechanical-dynamic model to characterize motorized machine tool spindles during very high speed rotation. Int J Mach Tools Manuf 43(10):1035–1050

    Article  Google Scholar 

  38. Wardle FP, Lacey SJ, Poon SY (1983) Dynamic and static characteristics of a wide speed range machine tool spindle. Precis Eng 5(4):175–183

    Article  Google Scholar 

  39. Cao YZ, Altintas Y (2004) A general method for the modeling of spindle-bearing systems. J Mech Design 126(6):1089–1104

    Article  Google Scholar 

  40. Jones AB (1960) A general theory for elastically constrained ball and radial roller bearings under arbitrary load and speed conditions. J Basic Eng 309-320

  41. Cao HR, Li B, He ZJ (2012) Chatter stability of milling with speed-varying dynamics of spindles. Int J Mach Tools Manuf 52(1):50–58

    Article  Google Scholar 

  42. Liu JF, Lai T, Tie GP (2018) Influence of thermo-mechanical coupled behaviors on milling stability of high speed motorized spindles. Precis Eng 52:94–105

    Article  Google Scholar 

  43. Ferry WB, Altintas Y (2008) Virtual five-axis flank milling of jet engine impellers—part I: mechanics of five-axis flank milling. J Manuf Sci Eng-Trans ASME 130(1):1–11

    Google Scholar 

  44. Ahmadi K, Ismail F (2012) Modeling chatter in peripheral milling using the semi discretization method. CIRP J Manuf Sci Technol 5(2):77–86

    Article  Google Scholar 

  45. Ji YJ, Wang XB, Liu ZB, Wang HJ, Wang KJ, Wang DQ (2019) Stability prediction of five-axis ball-end finishing milling by considering multiple interaction effects between the tool and workpiece. Mech Syst Signal Process 131:261–287

    Article  Google Scholar 

  46. Cao YZ, Altintas Y (2007) Modeling of spindle-bearing and machine tool systems for virtual simulation of milling operations. Int J Mach Tools Manuf 47:1342–1350

    Article  Google Scholar 

  47. Ertürk A, Ozguven HN, Budak E (2006) Analytical modeling of spindle–tool dynamics on machine tools using Timoshenko beam model and receptance coupling for the prediction of tool point FRF. Int J Mach Tools Manuf 46(15):1901–1912

    Article  Google Scholar 

  48. Liu ZF, Ma SM, Cai LG, Guo TN, Zhao YS (2012) Timoshenko beam-based stability and natural frequency analysis for heavy load mechanical spindles. J Mech Sci Technol 26(11):3375–3388

    Article  Google Scholar 

  49. Cao YZ (2006) Modeling of high-speed machine-tool spindle systems. The University of British Columbia, Vancouver

    Google Scholar 

  50. Feng W, Liu BG, Yao B, Cui ZM, He QS, Wang X (2018) An integrated prediction model for the dynamics of machine tool spindles. Mach Sci Technol 22(6):968–988

    Article  Google Scholar 

  51. Hu T, Yin GF, Sun MN (2014) Model based research of dynamic performance of shaft-bearing system in high-speed field. Shock Vib 1-12

  52. Ozturk E, Tunc LT, Budak E (2009) Investigation of lead and tilt angle effects in 5-axis ball-end milling processes. Int J Mach Tools Manuf 49(14):1053–1062

    Article  Google Scholar 

  53. Ozturk E, Budak E (2007) Modeling of 5-axis milling processes. Mach Sci Technol 11(3):287–311

    Google Scholar 

  54. Wang SB (2015) Automated five-axis tool path generation based on dynamic analysis. National University of Singapore, Singapore

    Google Scholar 

  55. Wang SB, Geng L, Zhang YF, Liu K, Ng TE (2016) Chatter-free cutter postures in five-axis machining. Proc Inst Mech Eng Part B-J Eng Manuf 230(8):1428–1439

    Article  Google Scholar 

  56. Schmitz TL, Smith KS (2008) Machine dynamics—frequency response to improved productivity. Springer, Berlin

    Google Scholar 

  57. Ji YJ, Wang XB, Liu ZB, Wang HJ, Jiao L, Lu Z, Huang T (2018) Milling stability prediction with simultaneously considering the multiple factors coupling effects—regenerative effect, mode coupling, and process damping. Int J Adv Manuf Technol 97(5–8):2509–2527

    Article  Google Scholar 

  58. Lu YA, Ding Y, Zhu LM (2017) Dynamics and stability prediction of five-Axis flat-end milling. J Manuf Sci Eng-Trans ASME 139(6):1–11

    Article  Google Scholar 

  59. Sadeghipour K, Cowley A (1988) The effect of viscous damping and mass distribution on the dynamic behaviour of a spindle-bearing system. Int J Mach Tools Manuf 28(1):69–77

    Article  Google Scholar 

  60. Elbestawi MA, Ismail F, Du R, Ullagaddi BC (1994) Modelling machining dynamics including damping in the tool-workpiece interface. J Eng Ind 116(4):435–439

    Article  Google Scholar 

Download references

Funding

This work is supported by the National Natural Science Foundation of China (Grant Nos. 51375055 and 51575055).

Author information

Authors and Affiliations

  1. Beijing Key Laboratory of Measurement & Control of Mechanical and Electrical System Technology, Beijing Information Science & Technology University, No. 12 East Qinghexiaoying Road, Beijing, 100192, People’s Republic of China

    Yongjian Ji & Hongjun Wang

  2. Key Laboratory of Fundamental Science for Advanced Machining, Beijing Institute of Technology, No. 5 Zhongguancun South Street, Haidian District, Beijing, 100081, People’s Republic of China

    Xibin Wang, Zhibing Liu, Yong Wang & Shuyao Liu

  3. School of Mechanical and Electronic Engineering, Henan University of Technology, High-tech District, Zhengzhou, 450001, Henan Province, People’s Republic of China

    Wei Feng

Authors
  1. Yongjian Ji
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xibin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhibing Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hongjun Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Wei Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Yong Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Shuyao Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yongjian Ji.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The original version of this article was revised: Equation 39 is missing in the original published paper.

Appendices

Appendix 1. Details of Tx1(90°),Tx2(90°),Ty(θB), Tz(θC),(TF‐ to ‐W)−1in Eq.(17)

$$ {\mathrm{T}}_{x1}\left({90}^{{}^{\circ}}\right)=\left[\begin{array}{ccc}1& 0& 0\\ {}0& \cos \left({90}^{{}^{\circ}}\right)& -\sin \left({90}^{{}^{\circ}}\right)\\ {}0& \sin \left({90}^{{}^{\circ}}\right)& \cos \left({90}^{{}^{\circ}}\right)\end{array}\right]\kern0.5em ,\kern0.5em {\mathrm{T}}_{x2}\left({90}^{{}^{\circ}}\right)=\left[\begin{array}{ccc}1& 0& 0\\ {}0& \cos \left({90}^{{}^{\circ}}\right)& \sin \left({90}^{{}^{\circ}}\right)\\ {}0& -\sin \left({90}^{{}^{\circ}}\right)& \cos \left({90}^{{}^{\circ}}\right)\end{array}\right] $$
(48)
$$ {\mathrm{T}}_y\left({\theta}_B\right)=\left[\begin{array}{ccc}\cos {\theta}_B& -\sin {\theta}_B& 0\\ {}\sin {\theta}_B& \cos {\theta}_B& 0\\ {}0& 0& 1\end{array}\right]\kern0.5em ,\kern0.5em {\mathrm{T}}_z\left({\theta}_C\right)=\left[\begin{array}{ccc}\cos {\theta}_C& -\sin {\theta}_C& 0\\ {}\sin {\theta}_C& \cos {\theta}_C& 0\\ {}0& 0& 1\end{array}\right] $$
(49)
$$ {\left({\mathrm{T}}_{\mathrm{F}\hbox{-} \mathrm{to}\hbox{-} \mathrm{W}}\right)}^{-1}=\left[\begin{array}{ccc}\cos {\alpha}_{\mathrm{F}}\cos {\gamma}_{\mathrm{F}}& \sin {\alpha}_{\mathrm{F}}& -\cos {\alpha}_{\mathrm{F}}\sin {\gamma}_{\mathrm{F}}\\ {}-\sin {\alpha}_{\mathrm{F}}\cos {\gamma}_{\mathrm{F}}& \cos {\alpha}_{\mathrm{F}}& \sin {\gamma}_{\mathrm{F}}\sin {\alpha}_{\mathrm{F}}\\ {}\sin {\gamma}_{\mathrm{F}}& 0& \cos {\gamma}_{\mathrm{F}}\end{array}\right] $$
(50)

Appendix 2. Details of p1, p2, p3, p4, e1, e2, e3, e4, o1, o2, o3, o4, f1, f2, f3, f4 in Eq. (47)

$$ {p}_1=\frac{-{m}_y{k}_x+{m}_{xy}{k}_{yx}}{m_x{m}_y-{m}_{xy}{m}_{yx}},{p}_2=\frac{-{m}_y{k}_{xy}+{m}_{xy}{k}_y}{m_x{m}_y-{m}_{xy}{m}_{yx}},{p}_3=\frac{-{m}_{yx}{k}_x-{m}_x{k}_{yx}}{m_x{m}_y-{m}_{xy}{m}_{yx}},{p}_4=\frac{-{m}_{yx}{k}_{xy}-{m}_x{k}_y}{m_x{m}_y-{m}_{xy}{m}_{yx}} $$
(51)
$$ {e}_1=\frac{-{m}_y{C}_x+{m}_{xy}{C}_{yx}}{m_x{m}_y-{m}_{xy}{m}_{yx}},{e}_2=\frac{-{m}_y{C}_{xy}+{m}_{xy}{C}_y}{m_x{m}_y-{m}_{xy}{m}_{yx}},{e}_3=\frac{-{m}_{yx}{C}_x-{m}_x{C}_{yx}}{m_x{m}_y-{m}_{xy}{m}_{yx}},{e}_4=\frac{-{m}_{yx}{C}_{xy}-{m}_x{C}_y}{m_x{m}_y-{m}_{xy}{m}_{yx}} $$
(52)
$$ {o}_1=\frac{-{m}_y\cdotp {h}_{2,11}+{m}_{xy}\cdotp {h}_{2,21}}{m_x{m}_y-{m}_{xy}{m}_{yx}},\kern0.5em {o}_2=\frac{-{m}_y\cdotp {h}_{2,12}+{m}_{xy}\cdotp {h}_{2,22}}{m_x{m}_y-{m}_{xy}{m}_{yx}} $$
(53)
$$ {o}_3=\frac{m_{yx}\cdotp {h}_{2,11}-{m}_x\cdotp {h}_{2,21}}{m_x{m}_y-{m}_{xy}{m}_{yx}},\kern0.5em {o}_4=\frac{m_{yx}\cdotp {h}_{2,12}-{m}_x\cdotp {h}_{2,22}}{m_x{m}_y-{m}_{xy}{m}_{yx}}, $$
(54)
$$ {f}_1=\frac{-{m}_y\cdotp {c}_{\mathrm{p}3,x}+{m}_{xy}\cdotp {c}_{\mathrm{p}3, yx}}{m_x{m}_y-{m}_{xy}{m}_{yx}},\kern0.5em {f}_2=\frac{-{m}_y\cdotp {c}_{\mathrm{p}3, xy}+{m}_{xy}\cdotp {c}_{\mathrm{p}3,y}}{m_x{m}_y-{m}_{xy}{m}_{yx}} $$
(55)
$$ {f}_3=\frac{m_{yx}\cdotp {c}_{\mathrm{p}3,x}-{m}_x\cdotp {c}_{\mathrm{p}3, yx}}{m_x{m}_y-{m}_{xy}{m}_{yx}},\kern0.5em {f}_4=\frac{m_{yx}\cdotp {c}_{\mathrm{p}3, xy}-{m}_x\cdotp {c}_{\mathrm{p}3,y}}{m_x{m}_y-{m}_{xy}{m}_{yx}} $$
(56)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ji, Y., Wang, X., Liu, Z. et al. Five-axis flank milling stability prediction by considering the tool-workpiece interactions and speed effect. Int J Adv Manuf Technol 108, 2037–2060 (2020). https://doi.org/10.1007/s00170-020-05251-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-020-05251-8

Keywords

Search

Navigation