Abstract
In the present study, we investigate different data-driven parameterizations for large eddy simulation of two-dimensional turbulence in the a priori settings. These models utilize resolved flow field variables on the coarser grid to estimate the subgrid-scale stresses. We use data-driven closure models based on localized learning that employs a multilayer feedforward artificial neural network with point-to-point mapping and neighboring stencil data mapping, and convolutional neural network fed by data snapshots of the whole domain. The performance of these data-driven closure models is measured through a probability density function and is compared with the dynamic Smagorinsky model (DSM). The quantitative performance is evaluated using the cross-correlation coefficient between the true and predicted stresses. We analyze different frameworks in terms of the amount of training data, selection of input and output features, their characteristics in modeling with accuracy, and training and deployment computational time. We also demonstrate computational gain that can be achieved using the intelligent eddy viscosity model that learns eddy viscosity computed by the DSM instead of subgrid-scale stresses. We detail the hyperparameters optimization of these models using the grid search algorithm.



















Similar content being viewed by others
References
Durbin, P.A.: Near-wall turbulence closure modeling without “damping functions”. Theor. Comput. Fluid Dyn. 3(1), 1 (1991)
Launder, B.E., Reece, G.J., Rodi, W.: Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 68(3), 537 (1975)
Meneveau, C., Katz, J.: Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 32(1), 1 (2000)
Mellor, G.L., Yamada, T.: Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 20(4), 851 (1982)
Bardina, J., Ferziger, J., Reynolds, W.: Improved subgrid-scale models for large-eddy simulation. In: 13th Fluid and Plasma Dynamics Conference, p. 1357 (1980)
Rogallo, R.S., Moin, P.: Numerical simulation of turbulent flows. Annu. Rev. Fluid Mech. 16(1), 99 (1984)
Erlebacher, G., Hussaini, M.Y., Speziale, C.G., Zang, T.A.: Toward the large-eddy simulation of compressible turbulent flows. J. Fluid Mech. 238, 155 (1992)
Frisch, U., Kolmogorov, A.N.: Turbulence: The Legacy of AN Kolmogorov. Cambridge University Press, Cambridge (1995)
Smagorinsky, J.: General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 91(3), 99 (1963)
Deardorff, J.W.: A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 41(2), 453 (1970)
Mcmillan, O., Ferziger, J., Rogallo, R.: Tests of subgrid-scale models in strained turbulence. In: 13th Fluid and Plasma Dynamics Conference, p. 1339 (1980)
Mason, P., Callen, N.: On the magnitude of the subgrid-scale eddy coefficient in large-eddy simulations of turbulent channel flow. J. Fluid Mech. 162, 439 (1986)
Piomelli, U., Moin, P., Ferziger, J.H.: Model consistency in large eddy simulation of turbulent channel flows. Phys. Fluids 31(7), 1884 (1988)
Germano, M., Piomelli, U., Moin, P., Cabot, W.H.: A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3(7), 1760 (1991)
Lilly, D.K.: A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A 4(3), 633 (1992)
Ghosal, S., Lund, T.S., Moin, P., Akselvoll, K.: A dynamic localization model for large-eddy simulation of turbulent flows. J. Fluid Mech. 286, 229 (1995)
Meneveau, C., Lund, T.S., Cabot, W.H.: A Lagrangian dynamic subgrid-scale model of turbulence. J. Fluid Mech. 319, 353 (1996)
Park, N., Mahesh, K.: Reduction of the Germano-identity error in the dynamic Smagorinsky model. Phys. Fluids 21(6), 065106 (2009)
Brunton, S.L., Noack, B.R., Koumoutsakos, P.: Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. (2019). https://doi.org/10.1146/annurev-fluid-010719-060214
Brenner, M., Eldredge, J., Freund, J.: Perspective on machine learning for advancing fluid mechanics. Phys. Rev. Fluids 4(10), 100501 (2019)
Kutz, J.N.: Deep learning in fluid dynamics. J. Fluid Mech. 814, 1 (2017)
Milano, Michele, Koumoutsakos, Petros: Neural network modeling for near wall turbulent flow. J. Comput. Phys. 182(1), 1 (2002)
Erichson, N.B., Mathelin, L., Yao, Z., Brunton, S.L., Mahoney, M.W., Kutz, J.N.: Shallow learning for fluid flow reconstruction with limited sensors and limited data. ArXiv preprint arXiv:1902.07358 (2019)
Fukami, K., Fukagata, K., Taira, K.: Super-resolution reconstruction of turbulent flows with machine learning. J. Fluid Mech. 870, 106 (2019)
Lee, K., Carlberg, K.: Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders. ArXiv preprint arXiv:1812.08373 (2018)
Murata, T., Fukami, K., Fukagata, K.: Nonlinear mode decomposition with convolutional neural networks for fluid dynamics. J. Fluid Mech. 882, A13 (2020)
Rudy, S.H., Brunton, S.L., Proctor, J.L., Kutz, J.N.: Data-driven discovery of partial differential equations. Sci. Adv. 3(4), e1602614 (2017)
Long, Z., Lu, Y., Ma, X., Dong, B.: PDE-net: learning PDEs from data. ArXiv preprint arXiv:1710.09668 (2017)
Raissi, M., Karniadakis, G.E.: Hidden physics models: machine learning of nonlinear partial differential equations. J. Comput. Phys. 357, 125 (2018)
Pathak, J., Hunt, B., Girvan, M., Lu, Z., Ott, E.: Model-free prediction of large spatiotemporally chaotic systems from data: a reservoir computing approach. Phys. Rev. Lett. 120(2), 024102 (2018)
Vlachas, P.R., Byeon, W., Wan, Z.Y., Sapsis, T.P., Koumoutsakos, P.: Data-driven forecasting of high-dimensional chaotic systems with long short-term memory networks. Proc. R. Soc. A Math. Phys. Eng. Sci. 474(2213), 20170844 (2018)
Raissi, M., Perdikaris, P., Karniadakis, G.E.: Numerical gaussian processes for time-dependent and nonlinear partial differential equations. SIAM J. Sci. Comput. 40(1), A172 (2018)
Pawar, S., Rahman, S.M., Vaddireddy, H., San, O., Rasheed, A., Vedula, P.: A deep learning enabler for nonintrusive reduced order modeling of fluid flows. Phys. Fluids 31(8), 085101 (2019)
Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686 (2019)
Erichson, N.B., Muehlebach, M., Mahoney, M.W.: Physics-informed autoencoders for Lyapunov-stable fluid flow prediction. ArXiv preprint arXiv:1905.10866 (2019)
Magiera, J., Ray, D., Hesthaven, J.S., Rohde, C.: Constraint-aware neural networks for Riemann problems. ArXiv preprint arXiv:1904.12794 (2019)
Ling, J., Kurzawski, A., Templeton, J.: Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 807, 155 (2016)
Wu, J.L., Xiao, H., Paterson, E.: Physics-informed machine learning approach for augmenting turbulence models: a comprehensive framework. Phys. Rev. Fluids 3(7), 074602 (2018)
Maulik, R., San, O., Rasheed, A., Vedula, P.: Subgrid modelling for two-dimensional turbulence using neural networks. J. Fluid Mech. 858, 122 (2019)
Mohebujjaman, M., Rebholz, L.G., Iliescu, T.: Physically constrained data-driven correction for reduced-order modeling of fluid flows. Int. J. Numer. Methods Fluids 89(3), 103 (2019)
Duraisamy, K., Iaccarino, G., Xiao, H.: Turbulence modeling in the age of data. Annu. Rev. Fluid Mech. 51, 357 (2019)
Lapeyre, C.J., Misdariis, A., Cazard, N., Veynante, D., Poinsot, T.: Training convolutional neural networks to estimate turbulent sub-grid scale reaction rates. Combust. Flame 203, 255 (2019)
King, R., Hennigh, O., Mohan, A., Chertkov, M.: From deep to physics-informed learning of turbulence: diagnostics. ArXiv preprint arXiv:1810.07785 (2018)
Wang, Z., Luo, K., Li, D., Tan, J., Fan, J.: Investigations of data-driven closure for subgrid-scale stress in large-eddy simulation. Phys. Fluids 30(12), 125101 (2018)
Taira, K.: Revealing essential dynamics from high-dimensional fluid flow data and operators. ArXiv preprint arXiv:1903.01913 (2019)
Tracey, B., Duraisamy, K., Alonso, J.: Application of supervised learning to quantify uncertainties in turbulence and combustion modeling. In: 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, p. 259 (2013)
Tracey, B.D., Duraisamy, K., Alonso, J.J.: A machine learning strategy to assist turbulence model development. In: 53rd AIAA Aerospace Sciences Meeting, p. 1287 (2015)
Ling, J., Ruiz, A., Lacaze, G., Oefelein, J.: Uncertainty analysis and data-driven model advances for a jet-in-crossflow. J. Turbomach. 139(2), 021008 (2017)
Sarghini, F., De Felice, G., Santini, S.: Neural networks based subgrid scale modeling in large eddy simulations. Comput. Fluids 32(1), 97 (2003)
Pope, S.: A more general effective-viscosity hypothesis. J. Fluid Mech. 72(2), 331 (1975)
Gamahara, M., Hattori, Y.: Searching for turbulence models by artificial neural network. Phys. Rev. Fluids 2(5), 054604 (2017)
Wang, J.X., Wu, J.L., Xiao, H.: Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data. Phys. Rev. Fluids 2(3), 034603 (2017)
Bhatnagar, S., Afshar, Y., Pan, S., Duraisamy, K., Kaushik, S.: Prediction of aerodynamic flow fields using convolutional neural networks. Comput. Mech. 64, 525–545 (2019)
Beck, A., Flad, D., Munz, C.D.: Deep neural networks for data-driven LES closure models. J. Comput. Phys. 398, 108910 (2019)
Srinivasan, P., Guastoni, L., Azizpour, H., Schlatter, P., Vinuesa, R.: Predictions of turbulent shear flows using deep neural networks. Phys. Rev. Fluids 4(5), 054603 (2019)
Pal, A.: Deep learning parameterization of subgrid scales in wall-bounded turbulent flows. ArXiv preprint arXiv:1905.12765 (2019)
Maulik, R., San, O.: A neural network approach for the blind deconvolution of turbulent flows. J. Fluid Mech. 831, 151 (2017)
Kraichnan, R.H.: The structure of isotropic turbulence at very high Reynolds numbers. J. Fluid Mech. 5(4), 497 (1959)
Kraichnan, R.H., Montgomery, D.: Two-dimensional turbulence. Rep. Prog. Phys. 43(5), 547 (1980)
Leith, C.: Atmospheric predictability and two-dimensional turbulence. J. Atmos. Sci. 28(2), 145 (1971)
Boffetta, G., Ecke, R.E.: Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44, 427 (2012)
Kraichnan, R.H.: Inertial ranges in two-dimensional turbulence. Phys. Fluids 10(7), 1417 (1967)
Batchelor, G.K.: Computation of the energy spectrum in homogeneous two-dimensional turbulence. Phys. Fluids 12(12), II (1969)
Leonard, A.: Advances in Geophysics, vol. 18, pp. 237–248. Elsevier, Amsterdam (1975)
Liu, S., Meneveau, C., Katz, J.: Experimental study of similarity subgrid-scale models of turbulence in the far-field of a jet. Appl. Sci. Res. 54(3), 177 (1995)
San, O.: A dynamic eddy-viscosity closure model for large eddy simulations of two-dimensional decaying turbulence. Int. J. Comput. Fluid Dyn. 28(6–10), 363 (2014)
Maulik, R., San, O.: A stable and scale-aware dynamic modeling framework for subgrid-scale parameterizations of two-dimensional turbulence. Comput. Fluids 158, 11 (2017)
Hagan, M.T., Demuth, H.B., Beale, M.H., De Jesús, O.: Neural Network Design, vol. 20. PWS Pub., Boston (1996)
Glorot, X., Bengio, Y.: Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, pp. 249–256 (2010)
Sutskever, I., Martens, J., Dahl, G., Hinton, G.: International Conference on Machine Learning, pp. 1139–1147 (2013)
Kingma, D.P., Ba, J.: Adam: a method for stochastic optimization. ArXiv preprint arXiv:1412.6980 (2014)
Ruder, S.: An overview of gradient descent optimization algorithms. ArXiv preprint arXiv:1609.04747 (2016)
Wan, L., Zeiler, M., Zhang, S., Le Cun, Y., Fergus, R.: International Conference on Machine Learning, pp. 1058–1066 (2013)
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., Salakhutdinov, R.: Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15(1), 1929 (2014)
Bartoldson, B.R., Morcos, A.S., Barbu, A., Erlebacher, G.: The generalization-stability tradeoff in neural network pruning. ArXiv preprint arXiv:1906.03728 (2019)
Zhu, L., Zhang, W., Kou, J., Liu, Y.: Machine learning methods for turbulence modeling in subsonic flows around airfoils. Phys. Fluids 31(1), 015105 (2019)
Xie, C., Wang, J., Li, H., Wan, M., Chen, S.: Artificial neural network mixed model for large eddy simulation of compressible isotropic turbulence. Phys. Fluids 31(8), 085112 (2019)
Yang, X., Zafar, S., Wang, J.X., Xiao, H.: Predictive large-eddy-simulation wall modeling via physics-informed neural networks. Phys. Rev. Fluids 4(3), 034602 (2019)
Krizhevsky, A., Sutskever, I., Hinton, G.E.: Imagenet classification with deep convolutional neural networks. Advances in Neural Information Processing Systems, pp. 1097–1105 (2012)
Ren, S., He, K., Girshick, R., Sun, J.: Faster r-cnn: towards real-time object detection with region proposal networks. Advances in Neural Information Processing Systems, pp. 91–99 (2015)
Kim, J., Kwon Lee, J., Mu Lee, K.: Accurate image super-resolution using very deep convolutional networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 1646–1654 (2016)
Dong, C., Loy, C.C., Tang, X.: Accelerating the super-resolution convolutional neural network. In: European Conference on Computer Vision. Springer, pp. 391–407 (2016)
Hou, W., Darakananda, D., Eldredge, J.: Machine learning based detection of flow disturbances using surface pressure measurements. In: AIAA Scitech 2019 Forum, p. 1148 (2019)
Nikolaou, Z.M., Chrysostomou, C., Vervisch, L., Cant, S.: Modelling turbulent premixed flames using convolutional neural networks: application to sub-grid scale variance and filtered reaction rate. ArXiv preprint arXiv:1810.07944 (2018)
Nikolaou, Z., Chrysostomou, C., Vervisch, L., Cant, S.: Progress variable variance and filtered rate modelling using convolutional neural networks and flamelet methods. Flow Turbul. Combust. 103, 1–17 (2019)
Tabeling, P.: Two-dimensional turbulence: a physicist approach. Phys. Rep. 362(1), 1 (2002)
Orlandi, P.: Fluid Flow Phenomena: A Numerical Toolkit, vol. 55. Springer, Berlin (2012)
San, O., Staples, A.E.: High-order methods for decaying two-dimensional homogeneous isotropic turbulence. Comput. Fluids 63, 105 (2012)
Kleissl, J., Kumar, V., Meneveau, C., Parlange, M.B.: Numerical study of dynamic Smagorinsky models in large-eddy simulation of the atmospheric boundary layer: validation in stable and unstable conditions. Water Resour. Res. 42(6), W06D10 (2006)
Galperin, B., Orszag, S.A.: Large Eddy Simulation of Complex Engineering and Geophysical Flows. Cambridge University Press, Cambridge (1993)
Khani, S., Waite, M.L.: Large eddy simulations of stratified turbulence: the dynamic smagorinsky model. J. Fluid Mech. 773, 327 (2015)
Moin, P., Squires, K., Cabot, W., Lee, S.: A dynamic subgrid-scale model for compressible turbulence and scalar transport. Phys. Fluids A 3(11), 2746 (1991)
Xu, Y., Fan, T., Xu, M., Zeng, L., Qiao, Y.: Spidercnn: deep learning on point sets with parameterized convolutional filters. Proceedings of the European Conference on Computer Vision (ECCV), pp. 87–102 (2018)
Trask, N., Patel, R.G., Gross, B.J., Atzberger, P.J.: GMLS-Nets: a framework for learning from unstructured data. ArXiv preprint arXiv:1909.05371 (2019)
Thomas, H., Qi, C.R., Deschaud, J.E., Marcotegui, B., Goulette, F., Guibas, L.J.: KPConv: flexible and deformable convolution for point clouds. ArXiv preprint arXiv:1904.08889 (2019)
Fey, M., Eric Lenssen, J.,Weichert, F., Müller, H.: SplineCNN: fast geometric deep learning with continuous B-spline kernels. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 869–877 (2018)
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., Bengio, Y.: Generative adversarial nets. Advances in Neural Information Processing Systems, pp. 2672–2680 (2014)
Acknowledgements
This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research under Award No. DE-SC0019290. Omer San gratefully acknowledges their support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Kunihiko Taira.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Disclaimer: This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
Appendices
Appendix A: Derivation of the Smagorinsky model in 2D turbulence
From Eq. 5, the subgrid-scale stresses in 2D field can be written as
The SGS stresses can be written as
where \(k_{\mathrm{SGS}}=\frac{1}{2}\tau _{kk}\) is called subgrid-scale kinetic energy (i.e., using the conventional summation notation with repeating indices, for example, \(\tau _{kk} = \tau _{11} + \tau _{22}\), in 2D). In Smagorinsky model, we model the deviatoric (traceless) part of SGS stresses as
where \(\nu _\mathrm{e}\) is the SGS eddy viscosity, and \({\bar{S}}_{ij}\) is called resolved strain rate tensor given by
where we can write explicitly as follows
The trace of the \({\bar{S}}\) is zero owing to the continuity equation for incompressible flows. Therefore, \({\bar{S}}_{ij}^d = {\bar{S}}_{ij}\) and the Smagorinsky model becomes
The eddy viscosity approximation computes \(\nu _\mathrm{e}\) using the following relation
where the proportionality constant is often set to \(C_k = 0.094\), and \(\varDelta \) is the length scale (usually grid size). The SGS kinetic energy \(k_{\mathrm{SGS}}\) is computed with the local equilibrium assumption of the balance between subgrid-scale energy production and dissipation
where the first term in the above equation is dissipation flux, second term is production flux, and the production constant is often set to \(C_{\epsilon }=1.048\). The double inner product operation : is given by
Substituting Eqs. 35 and 39 into Eq. 41, we get
From the above equations, subgrid-scale kinetic energy can be written as
where \(|{\bar{S}}| = \sqrt{2 {\bar{S}}_{ij} {\bar{S}}_{ij}}\). Furthermore, substituting Eq. 40 in the above equation, we get
We can define a new constant coefficient as
where \(C_\mathrm{s}=0.1678\) is called the Smagorinsky coefficient. Finally, we get following expression for SGS eddy viscosity
and the Smagorinsky model, given by Eq. 36, reads as
Appendix B: Hyperparameters optimization
In appendix, we outline the procedure we followed for selection of hyperparameters for ANN with point-to-point mapping and neighboring stencil mapping. For ANN, there are many hyperparameters such as number of neurons, number of hidden layers, loss function, optimization algorithm, activation function, and batch size, etc. If we use regularization, dropout, or weight decay to avoid overfitting, the design space of hyperparameters increases further.
We focus on three main hyperparameters of ANN: number of neurons, number of hidden layers, and learning rate of optimization algorithm. The training data are scaled between \([-1,1]\) using the minimum and maximum value in the training dataset. We use ReLU activation function given by \(\zeta (\chi ) = \text {max}(0,\chi )\), where \(\zeta \) is the activation function, and \(\chi \) is the input to the node. We use Adam optimization algorithm [71], and the batch size is kept constant at 256. Adam optimization algorithm has three hyperparameters: learning rate \(\alpha \), first moment decay rate \(\beta _1\), and second moment decay rate \(\beta _2\). We test our ANN for two learning rates \(\alpha =0.001\) and 0.0001. The other two hyperparameters in Adam optimization algorithm are \(\beta _1=0.9\) and \(\beta _2=0.999\). We employ mean-squared error as the loss functions, since it is a regression problem. We test both ANN with point-to-point mapping and neighboring stencil mapping for four different number of hidden layers \(L=2,3,5,7\). The ANN with point-to-point mapping is tested for four different number of neurons \(N=20,30,40,50\), and the local stencil mapping is tested for \(N=40,60,80,100\). The number of neurons is higher in case of local stencil mapping because there are more features compared to point-to-point mapping.
The optimal ANN architecture is selected using multi-dimensional gridsearch algorithm coupled with k-fold cross-validation. Cross-validation is a procedure used to determine the performance of the neural network on unseen data. The procedure consists of dividing the training data into k groups, training the ANN by excluding each group and evaluating the model’s performance on that group. Therefore, if we use fivefold cross-validation, then the model is trained five times and the performance index is computed for five groups. Once the performance for each group is available, the mean of the performance index is utilized to select optimal hyperparameters. We use 500 epochs for determining the optimal hyperparameters. A good learning is achieved when both training loss and validation loss reduce till the learning rate is minimal. We apply coefficient of determination \(r^2\) as the performance index to decide optimal hyperparameters. The calculation of coefficient of determination is done using the following formula
where \(y_i\) is the true label, \({\tilde{y}}\) is the predicated label, and \({\bar{y}}\) is the mean of true labels.
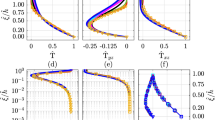
Figure 20 displays the performance index for ANN with point-to-point mapping and \({\mathbb {M}}3\) model for all hyperparameters tested using gridsearch algorithm. It can be observed that the performance of the network does not change significantly with hyperparameters and the difference in performance is very small. The optimal hyperparameters obtained for point-to-point mapping ANN are \(L=2\), \(N=40\), and \(\alpha =0.0001\). We use the same hyperparameters for other two models \({\mathbb {M}}1\) and \({\mathbb {M}}2\) for point-to-point mapping ANN. We see the similar behavior in case of neighboring stencil mapping ANN and model \({\mathbb {M}}3\) as shown in Fig. 21. The optimal hyperparameters for neighboring stencil mapping ANN are \(L=2\), \(N=40\), and \(\alpha =0.001\).
As discussed in Sect. 4.1, we get poor prediction between true and predicted stresses for point-to-point mapping with model \({\mathbb {M}}1\). Figure 22 shows the PDF of true and predicted stresses computed with different activation functions. It can be observed that the predicted stresses are almost the same for all activation functions. Therefore, we can conclude that we need additional input features such as velocity gradients to improve the prediction with point-to-point mapping.
Probability density function for SGS stress distribution with point-to-point mapping. The ANN is trained using \({\mathbb {M}}1{:}\,\,\{{{\bar{u}},{\bar{v}}}\} \rightarrow \{{\tilde{\tau }}_{11},{\tilde{\tau }}_{12},{\tilde{\tau }}_{22}\}\) with different activation functions. The training set consists of 70 time snapshots from time \(t=0.0\) to \(t=3.5\), and the model is tested for 400th snapshot at \(t=4.0\)
The CNN architecture has similar hyperparameters as the ANN. Additionally, we need to select the kernel shape and strides for CNNs. Stride is the amount by which the kernel should shift as it convolves around the volume. We use the stride = 1 in both x and y directions. We use \(3 \times 3\)-shaped kernel in our CNN architecture. We check the performance of CNN architecture for different number of hidden layers \(L=2,4,6,8\), different number of filters \(N=8,16,24,32\), and two learning rates. Figure 23 displays the performance index of CNN for different hyperparameters. The performance of CNN is more sensitive to the learning rate, and we observe stable performance for the learning rate \(\alpha =0.001\). The performance is almost similar for \(L=6,8,10\) with different number of kernels. We can select \(L=6\) and \(N=16\), which has performance index of 0.76. Additionally, we test the CNN architecture with \(L=6\) and [16, 8, 8, 8, 8, 16] distribution for the number of kernels along hidden layers and we observed the performance index of 0.75 at less computational cost. Therefore, we apply \(L=6\), \(N=[16,8,8,8,8,16]\), and \(\alpha =0.001\) as our hyperparameters for the CNN architecture.
Appendix C: CPU time measurements
In this study, the pseudo-spectral solver used for DNS is written in Python programming language. The code for coarsening of variables from fine to coarse grid, dynamic Smagorinsky model code is all written in Python. We use vectorization to get faster computational performance. The machine learning library Keras is also available in Python and is used for developing all data-driven closure models. Therefore, the CPU time reported in our analysis is for codes, which are all developed on the same platform. We would like to highlight that when the trained model is deployed, it makes the function for first time and hence it takes slightly more time. Once the function is created, the CPU time for deployment is less. Therefore, in all our tables, we report the CPU time for running the predict function second time since initializing CUDA kernels might yield a startup overhead as shown in Listing 1, where t1 here has some idle time due to initializing kernels. In our study, we report t2, and we further verified that t3 − t2 = t2, which illustrate that the reported CPU times are consistent.

Appendix D: ANN and CNN architectures
We use open-source Keras library to build our neural networks. It uses TensorFlow at the backend. Keras is widely used for fast prototyping, advanced research, and production due to its simplicity and faster learning rate. Keras library provides different options for optimizers, neural network architectures, activation functions, regularization, dropout, etc. Any simple neural network architecture can be coded with few lines of code. The sample code for ANN and CNN used in this work is listed in Listings 2 and 3.


Rights and permissions
About this article
Cite this article
Pawar, S., San, O., Rasheed, A. et al. A priori analysis on deep learning of subgrid-scale parameterizations for Kraichnan turbulence. Theor. Comput. Fluid Dyn. 34, 429–455 (2020). https://doi.org/10.1007/s00162-019-00512-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00162-019-00512-z