Micropolar medium in a funnel-shaped crusher

Abstract

In this paper, the solution to a coupled flow problem for a micropolar medium undergoing structural changes is presented. The structural changes occur because of a grinding of the medium in a funnel-shaped crusher. The standard macroscopic equations for mass and linear momentum are solved in combination with a balance equation for the microinertia tensor containing a production term. The constitutive equations of the medium describe a linear viscous material with a viscosity coefficient depending on the characteristic particle moment of inertia, the so-called microinertia. A coupled system of equations is presented and solved numerically in order to determine the distribution of the fields for velocity, pressure, viscosity coefficient, and microinertia in all points of the continuum. The numerical solution to this problem is found by using the implicit finite difference method and the upwind scheme.

1 Micropolar media undergoing structural change

1.1 Introductory remarks

Typically the microinertia tensor of a continuum particle, $\varvec{J}$, plays an important role in context with its rotational degrees of freedom, specifically in combination with the angular velocity vector, $\varvec{\omega }$, assigned to the continuum element. The details are outlined in Eringen’s theory of micropolar media; see, for example, [10]. The microinertia tensor obeys a kinematic constraint in form of a rate equation, which expresses the possibility of material continuum particles to undergo rigid body rotations. This feature is captured by means of three rotating rigid directors. Note that within the framework of this theory the form and shape of the microinertia tensor on the continuum scale does not change. Eringen calls such materials micropolar media. However, for describing processes of certain materials such a change is inevitable.

For this reason, a radical change of this concept has been presented recently in [16]. In this concept, the microinertia tensor is treated as a completely independent field variable for solid and fluid matter alike. Since the formulation is based on a spatial description, closed as well as open systems are allowed. A structural change due to the in- and outflux of matter or by external forces becomes possible. The microinertia tensor becomes a fully independent field variable with its own balance equation requiring additional constitutive quantities. More specifically, in contrast to the balance of mass, the balance for the microinertia tensor is not conserved. It contains a production term, $\varvec{\chi }$, which must be specified following the rules of constitutive theory.

In the following subsections, it will be demonstrated that this extended theory allows for the modeling of processes accompanied by a considerable structural change characterized by a changing microinertia within a representative volume element. The so-called crusher problem will be used for demonstration. This is a simulation problem of the movement and grinding of a granular medium in crushers of various geometries. Similar studies were considered previously in the literature in [2] and in simplified form by the authors in [11, 13], and [20].

Crusher problems are widely encountered in particle technology. This is due to the fact that one of the important parts of the process when creating new granular materials (for example, mineral fertilizers and plastics, medicines, seeds), as well as when enriching rocks, is to grind or to mill the particles of a granular material down to a certain size by crushing. Such experiments are described in [15] and [21]. Also, an experiment was conducted in [1], where the velocity profile at the exit of a so-called silo was studied, which represents the geometry of the crusher under consideration albeit for three-dimensional space.

It is also known that the viscosity of a medium is not constant. Rather it depends on many factors, such as temperature, strain rate, pressure, and others. For example, in [25] a crusher problem was considered, and the dependence of the viscosity coefficient on temperature was investigated. The crusher problem was also studied in [3]. However, in [3] the particle flux was limited, and the viscosity coefficient depended on the strain rate. In our work, we will take the dependence of viscosity on the average particle size into account, which can be represented by the microinertia tensor.

Despite the large amount of experimental data on the nature of the flow of bulk materials in various technological devices, there is currently no completely satisfying theory for the motion of granular media available. This paper contributes novel aspects to the theory. It is devoted to a coupled flow problem for a micropolar medium undergoing structural change in a funnel-shaped crusher.

More specifically, the main feature of our study consists in that a set of coupled equations for mass, linear momentum, and the balance of microinertia tensor with a production term is presented. Then this system is solved numerically for the first time in order to determine the distribution of the fields for velocity, pressure, viscosity coefficient, and the moment of microinertia. Besides that, another novelty of this paper is that the constitutive equations of the medium describe a linear viscous material with a viscosity coefficient depending on the characteristic particle moment of inertia. That means that a coupled problem is analyzed, in which the moment of inertia and the viscosity coefficient can change from position to position.

1.2 The balances of micropolar media

The motion of micropolar media in spatial description is described by the following coupled system of differential equations:

• balance of mass,

  $$\begin{aligned} \frac{\updelta \rho }{\updelta t}=-\rho \varvec{\nabla }\cdot \varvec{v}, \end{aligned}$$

  (1.1)

• balance of momentum,

  $$\begin{aligned} \rho \frac{\updelta \varvec{v}}{\updelta t}=\varvec{\nabla }\cdot \varvec{\sigma }+\rho \varvec{f}, \end{aligned}$$

  (1.2)

• balance of spin,

  $$\begin{aligned} \rho \varvec{J}\cdot \frac{\updelta \varvec{\omega }}{\updelta t}=-\varvec{\omega }\times {\varvec{J}}\cdot {\varvec{\omega }}+\varvec{\nabla }\cdot \varvec{\mu }+\varvec{\sigma }_\times +\rho \varvec{m}, \end{aligned}$$

  (1.3)

• balance of internal energy,

  $$\begin{aligned} \rho \frac{\updelta u}{\updelta t}=\varvec{\sigma }:\big (\nabla {\bigotimes }\varvec{v}+\varvec{{\mathrm {I}}}\times \varvec{\omega }\big )+\varvec{\mu }:\nabla {\bigotimes }\varvec{\omega }-\nabla \cdot \varvec{q}+\rho r, \end{aligned}$$

  (1.4)

where $\rho$ is the field of mass density, $\varvec{v}$ and $\varvec{\omega }$ are the linear and angular velocity fields, $\varvec{\sigma }$ is the non-symmetric Cauchy stress tensor, $\varvec{f}$ is the specific body force, $\varvec{J}$ is the specific microinertia tensor, $\varvec{\mu }$ is the non-symmetric couple stress tensor, $(\varvec{a}{\bigotimes }\varvec{b})_\times =\varvec{a}\times \varvec{b}$ is the Gibbsian cross, $\varvec{m}$ are specific body couples, u is the specific internal energy, $\varvec{q}$ is the heat flux, and r is the specific heat supply. By the colon, we denote the double scalar product between tensors of second rank, i.e., $\varvec{A}:\varvec{B}=A_{ij}B_{ij}$. Moreover,

$$\begin{aligned} \frac{\delta (\cdot )}{\delta t}=\frac{\partial (\cdot )}{\partial t}+\varvec{v}\cdot \nabla (\cdot ), \end{aligned}$$

(1.5)

is the substantial derivative of a field quantity $(\cdot )$ all of which need to be specified in spatial description.

It was already indicated that traditional micropolar theory assumes that each material point or “particle” of a micropolar continuum is phenomenologically equivalent to a rigid body. It can rotate, but the state of the principal components of the microinertia tensor in the principal axes system does not change. In other words, the microinertia tensor will not change its form nor shape; see, for example, [8, 10, 17, 23]. Even if a so-called micromorphic medium is considered, which in principle allows an intrinsic change of microinertia (following [7, 9, 10]), many publications use only the following additional equation for the conservation of microinertia (e.g., see [4, 22]), which is an identity of rigid body kinematics:

$$\begin{aligned} \frac{\updelta \varvec{J}}{\updelta t}=\varvec{\omega }\times \varvec{J}-\varvec{J}\times \varvec{\omega }\,. \end{aligned}$$

(1.6)

Note again that the terms on the right-hand side characterize the change of the inertia tensor, which is exclusively due to a rigid body rotation.

An extension to this approach was suggested in [6], where it was proposed that the microinertia of polar particles may change as the continuum deforms. This idea was further explored in [16], where it was clearly stated that the tensor of microinertia should be treated as an independent field. Within this approach, a fixed and open elementary volume V was treated as a micropolar continuum (macro-) region, as it is customarily done in spatial description. Then its microinertia tensor $\varvec{J}$ (in units of m$^2$) as a property on the continuum scale is obtained by homogenization as follows. Within the elementary volume V, there are $i=1, \ldots , N$ rigid microparticles of mass $m_i$ and microinertia tensor $\hat{\varvec{J}}_i$ (in units of kg m$^2$) such that:

$$\begin{aligned} \varvec{J}=\frac{1}{m}\sum \limits _{i=1}^N\hat{\varvec{J}}_i\;,\;\;m=\frac{1}{N}\sum \limits _{i=1}^Nm_i, \end{aligned}$$

(1.7)

where m is the average mass within V. Because of the motion of the medium, the elementary volume contains different microparticles as time passes, and the microinertia tensor assigned to the volume will change due to the incoming or outgoing flux of inertia. However, internal structural transformations are also possible. These are due to the combination or fragmentation of the particles during mechanical crushing, to chemical reactions, or to changes of the anisotropy of the material, for example by applying external electromagnetic fields. Such effects are explained in greater detail in [18,19,20] or [24]. In a nutshell, on the continuum scale all of this can be taken into account by adding a source or production term, $\varvec{\chi }$, to the right-hand side of Eq. (1.6), which now reads:

$$\begin{aligned} \frac{\updelta \varvec{J}}{\updelta t}=\varvec{\omega }\times \varvec{J}-\varvec{J}\times \varvec{\omega }+\varvec{\chi }\,. \end{aligned}$$

(1.8)

On the continuum level, this source term must be considered as a new constitutive quantity for which an additional constitutive equation has to be formulated. The form of the constitutive equation depends on the problem under consideration and can be a function of many physical quantities, such as temperature, pressure, and flow rate.

In our work, we will simulate a grinding process. Note that the microparticles in the funnel are very irregular in shape. However, the homogenized microinertia tensor at the continuum level is isotropic due to the statistically random distribution of microparticles of different sizes and shapes, $\varvec{J} = J\varvec{{\mathrm {I}}}$, where $\varvec{{\mathrm {I}}}$ denotes the unit tensor. Moreover, we will study a transient two-dimensional problem. Hence, $J = J(x,y,t)$. In the process of grinding, the size of the microparticles will decrease over time, which leads to a decrease in the moment of inertia, J, at the macrolevel. This is the structural change we wish to describe: The effectiveness of the milling process will be assessed by this parameter. Note that at the same time, the mass density of the elementary volume remains unchanged (see Fig. 1).

Fig. 1

Change of shape and corresponding homogenization, p is a process parameter, see text

Consequently, the source term in Eq. (1.8) must now take the following form,

$$\begin{aligned} \varvec{\chi }= \chi \varvec{{{\mathrm {I}}}}. \end{aligned}$$

(1.9)

i.e., the source term in Eq. (1.8) is also spherical.

In [11, 16], the following expression was proposed for the source term:

$$\begin{aligned} \chi = -\alpha _0p\big (J-J_*\big ) \end{aligned}$$

(1.10)

where $J_*$ and $\alpha _0$ are positive constants, p is the pressure in the material. They can be interpreted as follows. $J_*$ is related to the minimum grain size the particles can be crushed to, and $\alpha _0$ corresponds to the inverse of the particle toughness. As such, they are characteristics of the material and not of the crusher and may therefore be considered as constitutive properties. The minus sign indicates that the moment of inertia decreases with increasing pressure, p, in the material.

Finally in this section, it should be mentioned that the field of microinertia, i.e., the rotational inertia of the continuum, influences the development of the angular velocity $\varvec{\omega }$. This is determined by the spin balance (1.3), and this is usually the only purpose of $\varvec{J}$. In this paper, it is different: Because of the extended balance (1.8), $\varvec{J}$ can also be used to characterize structural changes of the micropolar medium. In fact, as it will be discussed below, in the present work we will exclusively concentrate on this feature.

2 Problem description

In a previous paper [12], the following (planar) funnel flow problem was considered. A continuous stream of bulk material flows from the top into the inlet orifice of a container of width 2L and height $H = H_1 + H_2$, such that the outlet narrows down to $2L_0$. The detailed geometry of this problem is shown in Fig. 2. However, in this previous paper we determined only velocity and pressure profiles. The indicated internal structural changes were not taken into account. In this paper, we will consider exactly the same geometry, but in addition to that, we will study particle grinding. Also, in the previous problem, the viscosity coefficient was constant for the entire considered area. Now we will analyze a coupled problem, in which the moment of inertia and the viscosity coefficient can change from position to position, which will affect the resulting velocity profile and vice versa.

Fig. 2

Particle transport in a channel and subsequent crushing in a funnel in 2D (stationary state)

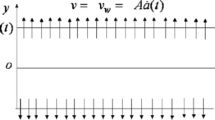
We assume that material is pushed into the inlet region of height $H_1$ and width 2L under a pressure $p_0$ as shown in the figure. Then the material enters a funnel region of height $H_2$ where the width narrows down linearly to $2L_0$. In this configuration, the angle between the walls of the funnel and the horizontal is (arbitrarily) given by $\alpha =45^\circ$. Geometric parameters relate to each other as $L_0 = 0.4L, 2L = H, H_1 = 0.7H$. Gravity points in the negative vertical direction,

$$\begin{aligned} \varvec{f}=-g\varvec{e}_y. \end{aligned}$$

(2.1)

Note that due to the fact that we are considering a plane problem, there will always be only two components of velocity.

We shall now discuss the boundary and the initial conditions.

• Initially the crusher region is completely empty. This means that the initial moment of inertia J and velocity components $v_x$ and $v_y$ in the crusher area are equal to zero.

  $$\begin{aligned} {J(x,y,t=0)}=0,\; {v_x(x,y,t=0)}=0,\; {v_y(x,y,t=0)}=0. \end{aligned}$$

  (2.2)

  Then particles keep entering the crusher at the top. Then they leave calculation area at the crusher bottom. Note that calculation area is $0<y<H$ and $-L<x<L$. (this is the area with green particles in Fig. 2.)

• On the left and right borders of the channel, and in particular in the funnel region, no slip boundary conditions are assumed at all times,

  $$\begin{aligned} {v_x}=0,\; {v_y}=0. \end{aligned}$$

  (2.3)

• The size of the particles entering the container region is the same; thus, the particles have the same moment of inertia $J_0$,

  $$\begin{aligned} J(x, y=H, t) = J_0. \end{aligned}$$

  (2.4)

• The following relations are used as boundary conditions for the pressures on the upper boundary of the system and at the end of the funnel, respectively:

  $$\begin{aligned} p(x, y=H, t) = p_0,\;p(x, y=0, t) = 0.\; \end{aligned}$$

  (2.5)

Also note that in this paper we will evaluate only situations when the particles have completely filled the crusher. The process of pouring in the particles leads a moving sharp front problem. Its accurate numerical simulation is quite difficult. It has been performed for 1D in [13]. However, the accurate modeling of the front is of no importance for what we wish to demonstrate in this paper.

In this paper, we consider the motion of an incompressible viscous medium the governing equation of which reads

$$\begin{aligned} \varvec{\sigma }=-p\varvec{{\mathrm {I}}}+\eta (J)\,\text {dev}\big (\nabla {\bigotimes }\varvec{v}+\varvec{v}{\bigotimes }\nabla \big ), \end{aligned}$$

(2.6)

where $\eta$ is the shear viscosity coefficient and p is the pressure.

It is also assumed that the material under consideration has a variable viscosity coefficient, and because the material is incompressible, Eq. (1.1) degenerates to

$$\begin{aligned} \varvec{\nabla } \cdot \varvec{v} = 0. \end{aligned}$$

(2.7)

A series of experiments were conducted in [26] to study the dependence of the viscosity coefficient on the particle diameter. The paper showed that the viscosity increases with decreasing particle diameter. The nature of the change is close to an exponential one. We assume that the dependence of the viscosity coefficient on the moment of inertia of the particles is similar to the dependence on the particle diameter. Then the particles with the least moment of inertia, $J_*$, should have a maximum viscosity, $\eta _*$. Based on this, we suppose that the viscosity of the material depends on the moment of inertia according to the following law:

$$\begin{aligned} \eta = \eta _0 + (\eta _* - \eta _0) \exp \left( -\lambda \frac{J - J_*}{J_*}\right) , \end{aligned}$$

(2.8)

where $\eta _0$, $\eta _*$ and $\lambda$ are positive constants. $\eta _0$ is the minimum viscosity that can be reached and corresponds to large values of microinertia $J=J_0$, whereas $\eta _*$ is the viscosity coefficient of particles with the smallest moment of inertia $J=J_*$ possible; in other words, it is the maximum resulting viscosity.

Given Eqs. (2.6), (2.7), (1.2) takes the following form ($\rho _0$ is the constant mass density),

$$\begin{aligned} \rho _0\frac{\updelta \varvec{v}}{\updelta t}=-\varvec{\nabla } p + 2 \varvec{\nabla } \cdot \big (\eta (J)\varvec{D}\big )+\rho _0\varvec{f}, \end{aligned}$$

(2.9)

where $\varvec{D} = \frac{1}{2}\big (\varvec{\nabla }{\bigotimes }\varvec{v} + \varvec{v}{\bigotimes }\varvec{\nabla }\big )$.

In general, Eqs. (1.1)–(1.3) and (2.7) were rewritten and solved in non-dimensional form:

$$\begin{aligned}&\frac{\partial \bar{J} }{ \partial \bar{t}} + \bar{v}_x\frac{\partial \bar{J} }{ \partial \bar{x}} + \bar{v}_y\frac{\partial \bar{J} }{ \partial \bar{y}} =-\bar{\alpha }\bar{p}\,(\bar{J}-1), \end{aligned}$$

(2.10)

$$\begin{aligned}&\frac{\partial \bar{v}_x}{ \partial \bar{x}} + \frac{\partial \bar{v}_y}{ \partial \bar{y}} = 0, \end{aligned}$$

(2.11)

$$\begin{aligned}&\frac{\partial \bar{v}_x }{ \partial \bar{t}} + \bar{v}_x \frac{\partial \bar{v}_x }{ \partial \bar{x}} + \bar{v}_y\frac{\partial \bar{v}_x}{ \partial \bar{y}} =-\frac{\partial \bar{p}}{\partial \bar{x}} + \bar{\eta }\left( \frac{ \partial ^2 \bar{v}_x}{\partial \bar{x}^2}+\frac{ \partial ^2 \bar{v}_x}{\partial \bar{y}^2}\right) + 2 \frac{ \partial \bar{\eta }}{\partial \bar{x}}\frac{ \partial \bar{v}_x}{\partial \bar{x}} + \frac{ \partial \bar{\eta }}{\partial \bar{y}}\left( \frac{ \partial \bar{v}_x}{\partial \bar{y}}+\frac{ \partial \bar{v}_y}{\partial \bar{x}}\right) , \end{aligned}$$

(2.12)

$$\begin{aligned}&\frac{\partial \bar{v}_y }{ \partial \bar{t}} + \bar{v}_x \frac{\partial \bar{v}_y}{ \partial \bar{x}} + \bar{v}_y \frac{\partial \bar{v}_y}{ \partial \bar{y}} =-\frac{\partial \bar{p}}{\partial \bar{y}} + \bar{\eta }\left( \frac{ \partial ^2 \bar{v}_y}{\partial \bar{x}^2}+\frac{ \partial ^2 \bar{v}_y}{\partial \bar{y}^2}\right) + 2 \frac{ \partial \bar{\eta }}{\partial \bar{y}}\frac{ \partial \bar{v_y}}{\partial \bar{y}} + \frac{ \partial \bar{\eta }}{\partial \bar{x}}\left( \frac{ \partial \bar{v}_x}{\partial \bar{y}}+\frac{ \partial \bar{v}_y}{\partial \bar{x}}\right) + \bar{g}.\qquad \end{aligned}$$

(2.13)

The bar on the various symbols refers to dimensionless quantities, namely

$$\begin{aligned} \begin{aligned}&\bar{x}=\frac{x}{H},\quad \bar{y}=\frac{y}{H},\quad \bar{v}_{x,y}=\frac{v_{x,y}}{\alpha _0p_cH}, \quad \bar{t}=\alpha _0p_ct,\quad \bar{p}=\frac{p}{\alpha _0^2p_c^2H^2\rho _0}, \quad \\&\bar{J}=\frac{J}{J_*}, \quad \bar{J_0}=\frac{J_0}{J_*},\quad \bar{\eta }=\frac{\eta }{\alpha _0p_cH^2\rho _0} \quad \bar{\alpha }=\alpha _0^2p_cH^2\rho _0,\quad \bar{g}=\frac{g}{\alpha _0^2p_c^2H}, \end{aligned} \end{aligned}$$

(2.14)

where $p_c = \rho _0gH_1$ is the hydrostatic pressure that is reached in the straight channel of height $H_1$. Note that we did not use the standard forms of non-dimensional quantities, since in order to introduce the standard parameters (such as the Reynolds number and Stokes number), we lacked some characteristic values (characteristic velocity and the characteristic time). In this context, Buckingham’s theorem should be mentioned, which tells us about the equivalence of various dimensionless procedures.

They were solved numerically based on the implicit finite difference method described in [5]. A spatially uniform finite difference mesh was introduced in the computational area. Velocity components $v_x, v_y$ were specified in mesh nodes. The pressure p and the moment of microinertia J were specified in the mesh cells. The second derivatives in the right-hand sides of equations ((2.12), (2.13)) were approximated with second order of accuracy in space. The convective terms in (2.10), (2.12), (2.13), as well as equation (2.11), were approximated with first order of accuracy using the upwind scheme (see [14], for example).

Unfortunately, there is no analytical solution available for the narrowing crusher problem. However, we can consider a solution that comes closest to the problem under consideration. This is the stationary Hagen–Poiseuille flow in a plane channel. For an incompressible fluid with constant viscosity under the influence of a constant pressure difference, we may write in this case:

$$\begin{aligned} v_y = -(q + \rho _0 g)\frac{1}{2\eta }(L^2 - x^2), \end{aligned}$$

(2.15)

where

$$\begin{aligned} \frac{\partial p}{\partial y} = \mathrm {const.} = q, \end{aligned}$$

(2.16)

and 2L denotes the width of the tunnel.

The Hagen–Poiseuille solution addresses the flow (rate) of an incompressible fluid flowing in a planar channel driven by a constant pressure gradient. Therefore, it will be possible to compare only the values obtained for the upper part of our vessel with the Hagen–Poiseuille solution, where there is no cross-sectional tapering. In other words, it cannot be used for comparison with velocities in the region of the narrowing funnel. Note that the results shown below are for the pressure $p_0 = 0$ on the upper border (see Eq. (2.5)). Despite the fact that the external pressure at the upper and lower boundaries of our vessel is equal to zero, we can still compare some of our results with the Hagen–Poiseuille solution. There is a driving force because of gravity, which pushes the flow. Indeed, as we will see later, the pressure in the narrowing region will increase and this will provide a pressure gradient in the part of the vessel without narrowing.

Finally some remarks about the spin balance (1.3) and the balance of internal energy (1.4) are due. As we discussed already, the purpose of the former equation is to determine the field of angular velocity, $\varvec{\omega }$, which is the kinematic measure of the internal rotational degree of freedom of the micropolar medium. It must not be confused with the vorticity given by $\frac{1}{2}\nabla \times \varvec{v}$. However, if it is intended to calculate this quantity, the applied constitutive equations must be adequate. For example, the stress tensor could not be of the simple Navier–Stokes form (2.6). Rather it would contain terms related to the difference between $\varvec{\omega }$ and the vorticity. This would make it antisymmetric and it would give a contribution to the production term $\varvec{\sigma }_\times$ in Eq. (1.3). Moreover, a constitutive relation for the couple stress tensor $\varvec{\mu }$ in terms of gradients of $\varvec{\omega }$ would be another logical requirement. In this paper, the angular velocity is simply zero. The same holds for the body couples $\varvec{m}$. Because the term $\varvec{\omega }\times \varvec{J}\cdot \varvec{\omega }$ vanishes for an isotropic microinertia, we conclude from Eq. (1.3) that the angular velocity vanishes in our case. To reiterate it once more, the intention of this paper is to demonstrate the potential of $\varvec{J}$ for modeling structural change and not its impact on the angular velocity.

On the other hand, the considered problem is clearly not isothermal because of the production term $\varvec{\sigma }:\nabla \varvec{v}$ in Eq. (1.4). In principle, the development of temperature during crushing could be computed numerically. However, this problem completely uncouples from the rest and this is not the focus of the present work. It will therefore not be considered any further.

3 Results

We present the stationary state based on a numerical solution of Eqs. (2.10)–(2.13). For this purpose, the following data were used ($\mathrm \Delta$ indicates grid spacing and time spacing):

$$\begin{aligned} \begin{aligned}&\bar{g}=0.907,\;\bar{\alpha }=1.575,\;\bar{J_0}=20,\;\bar{J_*}=1,\;2\bar{L}=1,\;\bar{H}=1,\;\\&\lambda =0.125,\;\Delta \bar{x}=0.005,\;\Delta \bar{y}=0.005,\;\Delta \bar{t}=0.001.\; \end{aligned} \end{aligned}$$

(3.1)

The grid spacing and time spacing were chosen such that the numerical solution was stable and convergent. The values of the other variables were chosen in such a way that the process under consideration could be most clearly demonstrated and for providing the most complete picture of the fields of all quantities. All results will be presented in dimensionless form.

In Figs. 3 and 4, the development of the absolute value of the horizontal velocity $\bar{v}_x$ and vertical velocity $\bar{v}_y$ in time is presented. The figures relate to four different points in time. It should be mentioned that, in general, the velocity component $\bar{v}_x$ is antisymmetric, whereas $\bar{v}_y$ is symmetric w.r.t. to symmetry axis.

In Fig. 3, we can see the distribution of the absolute value of the horizontal velocity $\bar{v}_x$ at four different points in time.

• In all inserts, we see a large red area in the upper region. There the velocity component $\bar{v}_x$ is almost zero, as expected due to the nature of the flow close to the analytical Hagen–Poiseuille type and to the initial conditions.

• We see how the horizontal velocity component $\bar{v}_x$, initially equal to zero, changes its value. It appears mostly only in the funnel region. The area in which the horizontal velocity is different from zero is not very large first time. However, this area and absolute value of velocity grow in time.

• We see that the horizontal velocity component $\bar{v}_x$ appears gradually not only in the narrowing region, but in the entire vessel (including small orange areas near the upper border of the vessel).

• The right bottom inset in the figure represents the situation for a time high enough to be comparable with the steady-state solution. Here and below, this conclusion seems justified because the relative difference between the two solutions at time $\bar{t}_4$ and the following point in time is less than 0.0001.

• In the second set of graphs at the bottom row, we see that the area with a vanishing horizontal value takes a conical shape. This behavior seems justified due to the form of the funnel.

Fig. 3

Distribution of the absolute value of the horizontal velocity $\bar{v}_x$ for four time points: $\bar{t}_1 = 0.00105, \bar{t}_2 = 0.0525, \bar{t}_3 = 0.105, \bar{t}_4 = 105$ (top to bottom, left to right, respectively)

In Fig. 4, we can see distribution of the absolute value of the vertical velocity $\bar{v}_y$ at four different points in time.

• The figures show that the vertical velocity component $\bar{v}_y$ is initially the same in almost the entire region and close to zero.

• We see that the area with a small vertical velocity (red–yellow) increases with time due to the narrowing region. Also note the vertical velocity increases in the region of the vessel center and decreases closer to the walls.

• The right bottom inset in the figures represents the situation for a time high enough to be comparable with the steady-state solution.

• In the quasi-stationary state (last inset), we see two red areas close to the walls, where the vertical velocity is close to zero. This means that in these areas the particles hardly move vertically, which gives them extra time for grinding.

Fig. 4

Distribution of the absolute value of the vertical velocity $\bar{v}_y$ for four time points: $\bar{t}_1 = 0.00105, \bar{t}_2 = 0.0525, \bar{t}_3 = 0.105, \bar{t}_4 = 105$ (top to bottom, left to right, respectively)

Figure 5 shows the close to a stationary state-based distribution of pressure and moment of microinertia in the vessel. Note that the time of this solution is $\bar{t}_4 = 105$.

• The distribution is symmetric w.r.t. the axis of symmetry as expected.

• In the funnel, the pressure is increasing near the wall, which corresponds to our expectations. This is advantageous for the grinding because the pressure enters the production term of microinertia, see Eq. (1.10).

• We see that at the outlet of the vessel there is also an orange region where the pressure is close to zero. This is due to the fact that particles “exit the vessel into free space” at the lower boundary, so to speak.

• In the right inset, we see the moment of inertia color plot. At the top of the vessel, there is a violet region that corresponds to the initial moment of inertia $\bar{J_0}$. In this area, the particles had not much time to grind.

• The red region corresponds to the minimum possible moment of inertia $\bar{J_*}$. We see that it is achieved in regions close to the vessel walls, as well as in the region of a narrowing cross section.

• Note that the moment of microinertia is less than its maximum value in the center of the exit. We can see a relatively large green area. This is due to the fact that particles from the narrowing region with a high horizontal velocity slow down the particles that move in the center. Therefore, central particles are longer under pressure and more effectively crushed.

• By comparing the two insets, we can see that in places of the funnel with high pressure the moment of inertia becomes less and vice versa. This is what we expect intuitively: A high pressure assists the crushing process. However, we note that the moment of microinertia depends not only just on the pressure, but also on the time the pressure is exerted on the particles. This is controlled by the two velocity components.

• The color plots for the viscosity coefficient are not shown in this figure, since the moment of inertia and the viscosity coefficient behave inversely to each other.

• We also see that on the line of symmetry where the vertical velocity component has a maximum, the moment of inertia does not change too much when particles move to the vessel bottom. This is because the particles with a high velocity are not experiencing a large pressure for a long time and there is not enough time for grinding.

Fig. 5

Distribution of the pressure (left) and the microinertia (right) in the vessel

Now we want to study the information contained in the distribution plots in more detail. The following figures show the distribution of quantities on the $\bar{x}$ and $\bar{y}$ axes in various cross sections. Due to the symmetry of the problem, we will present results for the right side of the crusher only. For a better understanding, which sections will be considered in the following graphs, Fig. 6 indicates the cross sections under consideration.

Fig. 6

Cross sections considered for the profiles of the velocity, pressure, and microinertia shown in Figs. 3,4 and 5

First, note that the analytical solution in Eq. (2.15) for the vertical velocity component was compared with the obtained numerical solution in the planar channel for a cross section at height $\bar{y} = 0.5$. It was found that both solutions are in good agreement with each other and the relative error between two solutions is less than one percent. A more detailed comparison can be found in [12].

Second, we consider the distribution of pressure in the vessel. The insets on the left and right of Fig. 7 show the profile of the pressure as a function of height $\bar{y}$ and of width $\bar{x}$, respectively.

• In the left inset, we see that the pressure is constant in several cross sections at large heights $\bar{y}$ as expected. Indeed, in the absence of a narrowing cross section, the solution is similar to the analytical solution in Eq. (2.15) for Hagen–Poiseuille flow in a plane channel, in which the pressure does not change in the cross sections.

• The right inset clearly shows how the pressure increases sharply with decreasing $\bar{y}$ coordinate when approaching the vessel exit. This is due to the fact that the particles fall into a narrower region. Because of that, the particles will grind more and we will see a sharp decrease in the microinertia. We also see a sharp decrease in pressure at very small values of the $\bar{y}$ coordinate and that at the vessel exit the pressure is close to zero due to “the release of particles into free space.”

• Note that here and below for some cross sections the curves on the graphs are “shorter” than for others. This is due to the fact that the cross sections of the vessel do not have the same length due to the narrowing. Therefore, some horizontal cross sections do not reach the value $\bar{x} = 1$, and some vertical cross sections do not reach $\bar{y} = 0$.

Fig. 7

Distribution of the pressure at various cross-sectional heights $\bar{y}$ and width $\bar{x}$ (left and right insets, respectively)

In the following, the change of microinertia and of the viscosity is analyzed. Figure 8 shows the distribution of the moment of microinertia as a function of width $\bar{x}$ and height $\bar{y}$ in various cross sections. From the figures, we conclude:

• In the left inset, we see that at heights $\bar{y} = 0.99$ the moment of inertia is equal to the initial value of $\bar{J_0}$ almost in the entire section, whereas in the wall region the microinertia decreases sharply and reaches the minimum value of $\bar{J_*}$ for all heights.

• When the cross-sectional coordinate approaches the vessel wall, the moment of inertia decreases sharply with decreasing height $\bar{y}$.

• The microinertia distribution in the vertical cross sections almost behaves like an exponential function and assumes the smallest values for all vertical cross section in the narrowing region, as expected.

Fig. 8

Moment of inertia distribution in horizontal and vertical cross sections (left and right insets, respectively)

The viscosity coefficient shows essentially the inverse behavior to the moment of inertia. Nevertheless, we will show it in the following graph in order to demonstrate the behavior of the viscosity coefficient clearly, depending on various sections. Figure 9 shows the viscosity coefficient distribution as a function of the width $\bar{x}$ and the height $\bar{y}$ in various cross sections. We see that:

• For the largest moments of inertia, the viscosity is smallest and vice versa.

• In the cross section at the height of $\bar{y} = 0.99$, the viscosity coefficient reaches its lowest value. We also see that over a certain length the viscosity coefficient in this cross section is constant. In this case, we can observe a distribution of the $\bar{v}_y$ velocity component closest to the analytical Hagen–Poiseuille solution of Eq. (2.15) shown in Fig. 11.

Fig. 9

Viscosity coefficient distribution in horizontal and vertical cross sections (left and right insets, respectively)

The left and right insets of Fig. 10 show the distribution of the horizontal and vertical velocity components, $\bar{v}_x$ and $\bar{v}_y$, respectively, as a function of width $\bar{x}$. Note that hereinafter plots for the absolute value of the vertical velocity will be presented.

• We can see that both velocity components disappear at the wall, as they should, and decrease as $\bar{y}$ increases. This seems logical, because the velocity increases downstream due to the narrowing and to the acceleration of gravity.

• We see that the vertical velocity reaches its maximum value in the section with a height of $\bar{y} = 0.01$. Also, with increasing height $\bar{y}$, the component $\bar{v}_y$ looks parabolic, which makes sense because of the analytical solution in Eq. (2.15) for the Poiseuille-type flow.

Fig. 10

Distribution of the horizontal and vertical velocities (left and right insets, respectively) at various horizontal cross-sectional width $\bar{x}$

Similarly, the insets on the left and right of Fig. 11 show the distribution of the horizontal and vertical velocity components, $\bar{v}_x$ and $\bar{v}_y$, as a function of height $\bar{y}$.

• We can see that the velocity component $\bar{v}_y$ becomes smaller when approaching the vessel wall. Also, for the cross section along the central axis of the vessel, the velocity component $\bar{v}_y$ sharply increases with decreasing $\bar{y}$ coordinate.

• As for the velocity component $\bar{v}_x$, we see that the distribution is rather complex. And we see that the component abruptly breaks off in some sections, as expected, due to the particles reaching the wall.

Fig. 11

Distribution of the horizontal and vertical velocities (left and right insets, respectively) at various vertical cross-sectional heights $\bar{y}$

Figures 12 and 13 show a comparison of the velocity profiles for two different cases. The dotted line shows the case with a constant viscosity coefficient (i.e., with $\lambda = 0$ for Eq. (2.8)). The solid line shows the case with a variable viscosity coefficient (i.e., with $\lambda = 0.125$). For comparison, different cross sections were chosen for different quantities in order not to overload the figures. In addition, sections were selected where the variables are nonzero.

In Fig. 12, we see that:

• The velocities in all sections are lower in the case of a variable viscosity coefficient. This is due to the fact that smaller particles (with a lower moment of inertia) have a higher viscosity coefficient, which means that the velocities of such particles become smaller. Because in all areas of the vessel the particles are crushed and reduced in size, we see a velocity decrease in all sections.

• We also see that the horizontal and vertical velocities do not increase so much for a variable viscosity coefficient when approaching the origin.

• On the left insert, in the cross section $\bar{y} = 0.6$ we see that the solutions do not differ much. This is due to the fact that at the top of the vessel the particles were not crushed much and the viscosity coefficient remained almost unchanged.

Fig. 12

Comparison of the horizontal and vertical velocities for constant and variable viscosity coefficient

Figure 13 shows that the moment of inertia in all sections is smaller for a variable viscosity coefficient. This means that the particles are crushed more leading to an increase in the viscosity coefficient. This seems logical, because with increasing viscosity of the medium, the velocity of the medium decreases. Particles are slower in the high-pressure region (in the narrowing region) and more strongly crushed.

Fig. 13

Comparison of the moment of inertia for constant and variable viscosity coefficient

Following up on this, we study the influence of the $\lambda$ parameter on viscosity in more detail in Fig. 14.

• The distribution of the moment of inertia at the exit from the vessel in question is presented on the left graph. We see that for a small $\lambda$ the moment of inertia shows a larger variation.

• Then the bigger the parameter $\lambda$, the faster the minimum moment of inertia is reached at the bottom of the vessel. This is due to the fact that the particles in the lower part of the vessel have a smaller diameter than at the beginning of the crusher, which means that the viscosity of such particles is higher. Due to the viscosity increase of the medium, the particle velocity in the lower region is greatly reduced, which means that the particles are longer under pressure, and as a result, they are more strongly crushed. This is exactly what is visible on the left inset.

• For $\lambda = 0.2$, the value of the moment of inertia over almost the entire cross section of the vessel exit dropped to the minimum value $\bar{J}_*$.

• On the right graph, we see that the moment of inertia distribution character in vertical cross sections tends to behave like an exponential function.

Fig. 14

Distribution of the moment of inertia of media with different viscosity coefficients at horizontal cross section $\bar{y} = 0.01$ and vertical cross section $\bar{x} = 0.2$ (left and right insets, respectively)

4 Conclusions and outlook

In this paper, the following was achieved:

• The importance of studying micropolar media was emphasized, since they allow modeling materials with an internal structure. This theory is suitable for studying many applied problems, in particular such of soil mechanics.

• A grinding process in the crusher was used as an example for these kind of problems.

• A numerical study of the flow of a granular micropolar medium through a two-dimensional funnel was carried out. For this, the Navier–Stokes equations and an additional equation for the change in microinertia were solved.

• Structural changes due to the grinding were shown.

• The viscosity coefficient of the medium was modeled as a variable, depending on the moment of inertia of the particles.

• The distribution of velocity, pressure, moment of inertia, and viscosity coefficient of the medium was obtained and discussed.

In the future, this problem can be expanded to become more complex. For example, one can consider a more sophisticated crusher geometry or a granular material with an uneven distribution of particles sizes and shapes. In this case, the rotation of the particles will have a significant effect on the medium and the average angular velocity of the representative volume will not be zero. Then the spin balance in Eq. (1.3) needs to be fully considered.

In addition, in some areas associated with the creation of materials from bulk media, the influence of temperature is important. Therefore, temperature processes as well as the dependence of the viscosity on the temperature in order to induce coupling can be added to the problem considered in this paper.

Finally, the incompressibility condition is questionable. In reality, there is space between the to-be-crushed particles. This space will become smaller with ongoing crushing, so that the compressibility will be affected. This will leave us with finding a constitutive equation for the pressure.