A Markovian random walk model of epidemic spreading

Abstract

We analyze the dynamics of a population of independent random walkers on a graph and develop a simple model of epidemic spreading. We assume that each walker visits independently the nodes of a finite ergodic graph in a discrete-time Markovian walk governed by his specific transition matrix. With this assumption, we first derive an upper bound for the reproduction numbers. Then, we assume that a walker is in one of the states: susceptible, infectious, or recovered. An infectious walker remains infectious during a certain characteristic time. If an infectious walker meets a susceptible one on the same node, there is a certain probability for the susceptible walker to get infected. By implementing this hypothesis in computer simulations, we study the space-time evolution of the emerging infection patterns. Generally, random walk approaches seem to have a large potential to study epidemic spreading and to identify the pertinent parameters in epidemic dynamics.

1 Introduction

Within the last two decades, network science has become a huge interdisciplinary field [1,2,3] recently driven by the significant upswing of online (social) networks and search engines with a burst of works focusing on human mobility and encounter networks [4]. It turned out that random walks in networks are especially powerful to cover spreading and diffusion phenomena widely observed in nature. These diffusion phenomena include so-called anomalous diffusion which have been successfully described by space-time fractional partial differential diffusion equations [5].

On the other hand within the last two decades, an impressive amount of scientific work has been devoted to epidemic spreading models. For an introduction in epidemic modeling and state-of-the-art models such as the ‘SIR model’ ($S=$ susceptible, $I=$ infected, $R=$ recovered), we refer to [6]. It is natural that the present worldwide pandemic context of COVID-19 is boosting an additional interest to this topic [7, 8]. Epidemic spreading in complex networks was studied by several authors [9,10,11] and the epidemic dynamics in scale-free networks was analyzed in [12]. In a recent paper, the effects of quarantine measures to epidemic spreading in activity-driven adaptive temporal networks were studied [13] including percolation effects in epidemic spreading in small-world networks [14, 15]. A renormalization group approach has been employed to model the second COVID-19 wave in Europe [16], just to quote a few examples.

Strongly driven by the present world-wide COVID-19 spreading there is a huge and urgent need of reliable models that are able to capture essential aspects of the space-time dynamics of infectious diseases allowing to develop preventive strategies. For an overview of the present world-wide COVID-19 situation as far known, we refer to [17].

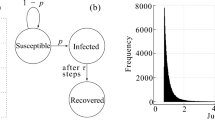
Infectious diseases such as measles, mumps, and rubella can be studied in the framework of nonlinear dynamical systems. For the most simple case of spatially homogeneous infection rates, SIR models have been applied successfully in the past [18, 19]. As mentioned, SIR stands for the three compartments susceptible–infected–recovered into which the individuals are grouped, depending on their state. A susceptible individual (S) can be infected and become ill (I). After a certain time $\tau _1$, it will recover and be removed from the system (R) in the subsequent computer simulation model. During time $\tau _1$, it can infect other susceptible individuals. The mathematical description in the SIR model is achieved by an ordinary first-order differential equation for each rate. If spatial effects are taken into account, the rates can be assumed space-dependent and a set of three nonlinear coupled diffusion equations can be derived [6].

Instead of using partial differential equations, the individuals or particles can be considered as independent random walkers on a discrete network with a given architecture. Our model is based on the following assumptions. The particles perform random jumps from one node to another connected node of the network. If on the same node an infected particle meets a susceptible one, the susceptible walker may be infected with a given probability P. To describe the process of recovery, each particle has an inner variable parametrizing its state. This variable changes in course of time. If ’time’ is assumed to be discrete, the whole dynamics on the network and of the inner variable can be formulated as a (nonlinear) mapping from one-time step to the next. The system has no memory, its state is uniquely defined by the positions of the particles and the values of their inner variables at a certain time step (Markov process).

Our paper is organized as follows. In the subsequent Sect. 2, we give a brief general introduction into the dynamics of Z independent Markovian random walkers on finite connected (ergodic) graphs. Without loss of generality, we confine us here to undirected graphs. We utilize the Markovian walk approach to derive an upper bound for the so-called basic reproduction number $R_0$ which is defined subsequently. In this part, we consider the situation when there is a single infected walker and $Z-1$ susceptible walkers in the network. We derive explicit formulae for the expected number of times the infected walker meets a susceptible one which defines an upper bound for $R_0$.

In Sect. 3, we perform numerical simulations employing above mentioned assumptions to generate space-time patterns of the susceptible/infected walkers where we consider Z independent walkers on a finite 2D square lattices with variable adjacency matrices and connectivity. In this way, we explore how the architecture of a network affects the space-time dynamics of the epidemic spreading and identify pertinent parameters governing the space-time patterns in order to establish predictive measures such as confinement and social distance rules.

2 Multiple random walkers model

2.1 Some basic features

In the present section, we recall some basic features of random walks with independent multiple walkers on the network [20] (See also [4, 21, 22] for outlines and analysis of the emergent space-temporal dynamics which we employ in our model). We focus on unbiased Markovian walks, however, this approach can be generalized to biased walks on directed graphs and also to continuous-time random walks (CTRWs). We consider Z independent random walkers $r=1,\ldots Z$ on a connected undirected network of $p=1,\ldots , N$ nodes. Despite the results of the present section can be derived in a simpler way, the approach recalled here allows to be applied to elaborate more sophisticated models such as for instance when the walkers perform independent CTRWs.

We assume that the walkers move independently through the network where the jumps of a walker r are governed by his own $N\times N$ one-step transition matrix ${\mathbf {W}}^{(r)}$ with the elements $W^{(r)}_{ij}$ ($i,j=1,\ldots , N$, $r=1,\ldots , Z$) indicating the probability of the transition between the nodes $i \rightarrow j$ in one jump with $\sum _{j=1}^NW^{(r)}_{ij}=1$ and $0\le W^{(r)}_{ij} \le 1$, i.e., per construction the transition matrices ${\mathbf{W}}^{(r)}$ are row-stochastic. Further, we assume that all walkers jump synchronously at integer times $t=1,2,\ldots \in \mathbb {N}$ and occupy at $t=0$ their respective departure nodes. Performing its nth jump at $t=n$, each walker remains during $t\in [n,n+1)$ on the node he has reached at $t=n \in \mathbb {N}_0$. For convenience, we employ Dirac’s $\langle \mathrm{bra}|-|\mathrm{ket}\rangle$ notation with $|\mathbf {i}\rangle =|i_1,i_2,\ldots ,i_Z\rangle =|i_1\rangle |i_2\rangle \ldots | i_Z\rangle$ where $i_r$ indicates the node occupied by walker r. We refer $|\mathbf {i}\rangle$ to as ‘state-vector’ containing the positions of the walkers in the network. The collective dynamics of the Z independent walkers is then characterized by the collective one-step transition matrix¹

$$\begin{aligned} \mathcal{W}_{\mathbf {i},\,\mathbf {j}} = \langle \mathbf {i}|\mathcal{W}|\mathbf {j}\rangle = \prod _{r=1}^Z W^{(r)}_{i_r,j_r}. \end{aligned}$$

(1)

Assuming walker r starts at $t=0$ at node $i_r$, then the probability to find the walker r on node $j_r$ at time t is given by

$$\begin{aligned} \mathcal{P}^{(r)}_{i_rj_r}(t)=\langle i_r|({\mathbf {W}}^{(r)})^t|j_r\rangle ,\quad t \in \mathbb {N}_0 \end{aligned}$$

(2)

where for $t=0$ we assume here the initial condition $\mathcal{P}^{(r)}_{i_rj_r}(t)|_{t=0}=\delta _{i_rj_r}$. In this relation we assume that each walker $r=1,\ldots ,Z$ moves independently through the graph in a Markovian walk governed by the master equation

$$\begin{aligned} P_{ij}^{(r)}(t+1) = \sum _{k=1}^N P_{ik}^{(r)}(t)W^{(r)}_{kj} ,\quad P_{ij}^{(r)}(0)=\delta _{ij} , \quad r=1,\ldots , Z \end{aligned}$$

(3)

thus $P_{ij}^{(r)}(t)=\langle i |{\mathbf {W}}^{(r)})^t| j\rangle$ indicates the probability of walker r to reach node j in t jumps when departing at $t=0$ from node i. When all walkers hop synchronously at $t\in \mathbb {N}_0$ the probability to find the Z walkers in the state $|\mathbf {j}\rangle =|j_1,j_2,\ldots ,j_Z\rangle$ at time t becomes

$$\begin{aligned} \mathcal{P}(\mathbf {i},\mathbf {j},t) = \prod _{r=1}^Z \mathcal{P}^{(r)}_{i_r j_r}(t) \end{aligned}$$

(4)

with $\mathcal{P}^{(r)}(\mathbf {i},\mathbf {j},t)|_{t=0} =\delta _{\mathbf {i},\,\mathbf {j}} = \prod _{r=1}^Z \delta _{i_r j_r}$. In order to develop such a model we are interested in the ‘state-probabilities,’ i.e., the probabilities that the nodes $j=1,\ldots , N$ are occupied by $s_1,\ldots , s_N$ ($\sum _{j=1}^N s_j = Z$) walkers. For our convenience, we introduce the following generating functions

$$\begin{aligned} G^{(r)}_{i_r}(u_1,\ldots , u_N,t)=\mathcal{P}^{(r)}(t)\cdot \mathbf {u} = \sum _{s=1}^N \mathcal{P}^{(r)}_{i_r s}(t)u_s ,\quad r = 1,\ldots , Z \end{aligned}$$

(5)

with $G^{r}_{i_r}(u_1=1,\ldots , u_N=1,t)=\sum _{j=1}^NP_{ij}^{(r)}(t) = 1$ reflecting normalization. Now consider the collective generating function

$$\begin{aligned} \begin{array}{clc}\displaystyle \mathcal{G}_{\mathbf {i}}(\xi \mathbf {u},t) &{} = \displaystyle \mathcal{G}_{\mathbf {i}}(\xi u_1,\ldots , \xi u_N,t)= \prod _{r=1}^Z G^{r}_{i_r}(\xi u_1,\ldots , \xi u_N,t) &{} \\ \\ &{}= \displaystyle \xi ^Z \sum _{s_1+s_2+ \cdots s_N = Z \, (0\le s_i \le Z)}\mathcal{A}_{\mathbf {i}}(s_1,s_2,\ldots ,s_N,t) u_1^{s_1} u_2^{s_2}\ldots u_N^{s_N} &{} \end{array} \end{aligned}$$

(6)

which is a multinomial of total degree Z. The coefficients ($s_i= 0,1,\ldots , Z$)

$$\begin{aligned} \mathcal{A} _{\mathbf {i}}(s_1,s_2,\ldots ,s_N,t) =\frac{1}{s_1!s_2!\ldots s_N!} \frac{\partial ^Z}{\partial u_1^{s_{1}}\partial u_2^{s_{2}}\ldots \partial u_N^{s_N}}\mathcal{G}_{\mathbf {i}}(\mathbf {u},t)|_{|u\rangle = \mathbf {0}} \end{aligned}$$

(7)

indicate the state-probabilities, i.e., the probabilities that the nodes $1,2,\ldots , N$ at time t and with the given initial condition are occupied by $s_1,s_2,\ldots ,s_N$ walkers (where $s_1+s_2+\cdots +s_N=Z$ recovers the total number of walkers). We observe that $\mathcal{G}_{\mathbf {i}}(u_1,\ldots ,u_N,t)\big |_{u_1=\ldots =u_N=1}=1$, i.e., (7) indeed is a normalized distribution. We further observe that since (6) is a homogeneous function of total degree Z, namely $\mathcal{G}_{\mathbf {i}}(\xi u_1,\ldots , \xi u_N,t)= \xi ^Z \mathcal{G}_{\mathbf {i}}(u_1,\ldots , u_N,t)$ thus holds the homogeneity relation

$$\begin{aligned} \frac{d}{d\xi }\mathcal{G}_{\mathbf {i}}(\xi u_1,\ldots , \xi u_N,t)|_{\xi =1} = \sum _{j=1}^N u_j\frac{\partial }{\partial u_j} \mathcal{G}_{\mathbf {i}}(u_1,\ldots ,u_N,t) = Z \mathcal{G}_{\mathbf {i}}(u_1,\ldots , u_N,t) \end{aligned}$$

(8)

with

$$\begin{aligned} \sum _{j=1}^N u_j\frac{\partial }{\partial u_j} \mathcal{G}_{\mathbf {i}}( u_1,\ldots , u_N,t)\bigg |_{u_1=\ldots =u_N=1} =Z. \end{aligned}$$

(9)

As an important case let us consider when all walkers have identical transition matrix $W^{(r)}_{ij}=W_{ij}$ and identical departure node $i_r=i$ $\forall r=1,\ldots Z$. Then, with (2) ($P_{ij}(t)=P^{(r)}_{ij}(t)$) we get for (6) the relation

$$\begin{aligned} \mathcal{G}^{(Z)}_{\mathbf {i}}(u_1,\ldots , u_N,t) = \left( \sum _{j=1}^NP_{ij}(t)u_j\right) ^Z \end{aligned}$$

(10)

with the state-probabilities given by the multinomial-coefficients

$$\begin{aligned} \mathcal{A}^{(Z)}_{\mathbf {i}}(s_1,s_2,\ldots ,s_N,t)= \frac{Z!}{s_1!s_2!\ldots s_N!} (P_{i1}(t))^{s_1}(P_{i2}(t))^{s_2}\ldots (P_{iN}(t))^{s_N} \end{aligned}$$

(11)

where $s_1+s_2+\cdots +s_N=Z$ and $s_{j} \in [0,Z]$.

Case: $N=2$

For illustration, let us consider a network of two nodes $i=1,2$ ($N=2$) where we have Z independent walkers and let us assume the initial condition $i_r=1$ for all Z walkers. Let us assume all walkers have the same transition matrix $W^{(r)}_{ij}=W_{ij}$. Then, the collective generating function (6) is given by

$$\begin{aligned} \begin{array}{clc} \displaystyle \mathcal{G}_{(1,1)}(u_1,u_2,t) &{} = \displaystyle (P_{11}(t)u_1+P_{12}(t)u_2)^Z&{} \\ \\ {} &{} = \displaystyle \sum _{s=0}^Z \left( \begin{array}{l} Z \\ s\end{array}\right) (P_{11}(t))^s(P_{12}(t))^{Z-s} u_1^su_2^{Z-s}&\end{array} \end{aligned}$$

(12)

where $\left( \begin{array}{l} Z \\ s\end{array}\right) = \frac{Z!}{s! (Z-s)!}$ indicate the binomial-coefficients. Hence, the state-probabilities, i.e., probabilities that (with the given initial condition) at time t node 1 is occupied by s walkers and node 2 by $Z-s$ walkers are obtained as

$$\begin{aligned} \mathcal{A}_{(1,1)}(s,Z-s,t)= \left( \begin{array}{l} Z \\ s\end{array}\right) (P_{11}(t))^s(P_{12}(t))^{Z-s} ,\quad s \in [0,Z]. \end{aligned}$$

(13)

The normalization of the state-probability distribution again is easily verified $\sum _{s=0}^N\mathcal{A}_{1,1}(s,Z-s,t)=\mathcal{G}_{\mathbf {i}=(1,\ldots 1)}(1,1,t)= (P_{11}(t)+P_{12}(t))^Z=1$.

Now we need to relate the architecture of the graph with its random walk features. The information of the topology of an undirected graph is contained in the one-step transition matrix [1, 24]

$$\begin{aligned} W_{ij}= \delta _{ij}-\frac{1}{K_i}L_{ij} \end{aligned}$$

(14)

where we assume that each walker undertakes jumps on the graph governed by the same one-step transition matrix. In (14), we introduced the $N\times N$ Laplacian matrix

$$\begin{aligned} L_{ij} = K_i\delta _{ij} -A_{ij} \end{aligned}$$

(15)

which contains the adjacency matrix $A_{ij}$ with $A_{ij}=1$ if the nodes i, j are connected by an edge and $A_{ij}=0$ else. Further, we do not allow self-connections which is expressed by $A_{ii}=0$. In undirected networks the edges do not have a direction, i.e., the adjacency matrix and the Laplacian matrix are symmetric. Further important is the degree $K_i$ of a node i which counts the number of nodes connected with i, namely

$$\begin{aligned} K_i = \sum _{j=1}^NA_{ij} \end{aligned}$$

(16)

where the condition $K_i >0$ tells us that there are no isolated disconnected nodes. With (15), the transition matrix (14) can also be written as

$$\begin{aligned} W_{ij} =\frac{1}{K_i}A_{ij} \end{aligned}$$

(17)

where we directly verify row-stochasticity $\sum _{j=1}^NW_{ij}=1$. Per construction, we have $W_{ii}=0$ thus the walkers at any time step have to move and change the node. The transition matrix is non-symmetric if there are nodes with variable degree $K_i\ne K_j$. For later use, we introduce the canonical representation (For a detailed spectral analysis of spectral properties, see [24])

$$\begin{aligned} {\mathbf {W}}= |\varPhi _1\rangle \langle {\bar{\varPhi }}_1| + \sum _{m=2}^N \lambda _m |\varPhi _m\rangle \langle {\bar{\varPhi }}_m| \end{aligned}$$

(18)

where $|\varPhi _s\rangle$ and $\langle {\bar{\varPhi }}_s|$ denote the right- and left eigenvectors of ${\mathbf {W}}$, respectively, and we assume an aperiodic ergodic (connected) network with the eigenvalue structure $|\lambda _s|\le 1$ with real eigenvalues $\lambda _s \in \mathbb {R}$ where the largest unique (Frobenius-) eigenvalue is $\lambda _1=1$ and $-1< \lambda _m < 1$ for $m=2,\ldots N$. We thus have the unique stationary distribution

$$\begin{aligned} {\mathbf {W}}^{\infty } = \lim _{n\rightarrow \infty }{\mathbf {W}}^n = |\varPhi _1\rangle \langle {\bar{\varPhi }}_1| \end{aligned}$$

(19)

as $\lambda _m^n \rightarrow 0$ ($m=2,\ldots N$) with the elements [24]

$$\begin{aligned} W_{ij}^{(\infty )} = W_j^{(\infty )}= \frac{K_j}{\mathcal{K}} ,\quad {\mathcal{K}}=\sum _{j=1}^N K_j = N \langle K\rangle \end{aligned}$$

(20)

where ${\mathcal{K}}$ is called the total degree and $\langle K\rangle$ denotes the average degree of the network. It is important to notice that in (aperiodic) ergodic (i.e., connected) networks the stationary distribution has uniquely (nonzero) positive elements $W_{ij}^{(\infty )}=W^{(\infty )}_j >0$ and is given by the normalized degrees independent of the departure node i. The stationary transition matrix is a matrix consisting of identical rows (see, e.g., [24] for an analysis of the related spectral properties of the transition matrix in ergodic graphs). Having recalled these general features, we can now use these properties to derive estimates for the reproduction numbers which are key quantities in epidemic models.

2.2 Upper bounds for reproduction numbers

We now consider the situation of Z independent walkers where one walker is infectious in the time interval $0\le t \le \tau _1$. We denote the infectious walker by $r=1$ and $Z-1$ walkers (denoted by $r=2, \ldots Z$) are susceptible. For later use let us introduce the ‘effective reproduction number’ $R_e(\tau _1)$ as the number of infections an infectious walker causes up to time $\tau _1$ while he is infectious. Apart of this quantity the so-called basic reproduction number $R_0(\tau _1)$ is of interest. $R_0(\tau _1)$ indicates the number of newly infected walkers (up to time $\tau _1$) by one infected walker under the assumption the infected walker meets only susceptible walkers. In fact $R_e$ also depends on time by the time-dependence of the number of susceptible walkers. In the present part, in order to derive an upper bound, we ignore this time-dependence. On the other hand, the quantity $R_0$ ignores the fact that an infectious walker does not only meet susceptible ones, but also infected and recovered walkers. Therefore, $R_0 \ge R_e$, i.e., the basic reproduction number overestimates the ‘real’ effective reproduction number $R_e$. For $R_e >1$, the number of infected walkers is increasing. If $R_e >1$ is persisting over longer times, then we are in the regime of (exponential) epidemic spreading. For $R_e = 1$, the number of infected walkers remains stable, and for $R_e < 1$, the number of infected walkers is decreasing and when persisting over longer times then the epidemics dies out.

Now for the sake of simplicity in the formulas to be derived, we assume for the susceptible walkers random initial conditions and stationary distributions, namely

$$\begin{aligned} P_{ij}^{(s)}(t)= W_j^{(\infty )}=\frac{K_j}{\mathcal{K}} ,\quad s=2,\ldots ,Z \end{aligned}$$

(21)

independent of time. In order to get an upper bound for the basic reproduction number, we are now interested in the expected number of times ${\hat{\mathcal{R}}}(\tau _1)$ the infectious walker meets another walker (no matter whether or not susceptible) during the time $\tau _1$ of his infection. Clearly ${\hat{\mathcal{R}}}(\tau _1) \ge R_0(\tau _1)$, i.e., ${\hat{\mathcal{R}}}(\tau _1)$ represents an upper bound for the basic reproduction number $R_0(\tau _1)$. The quantity ${\hat{\mathcal{R}}}(\tau _1)$ ignores also the fact that the infectious walker may multiply meet the same susceptible walker. We come back to the issue of variable ‘susceptibility’ with a probability P of infection as a crucial parameter later on. For the susceptible walkers in the stationary state, the generating function (10) becomes independent of their initial nodes and of time (as we ignore transitions from susceptible to the infectious state) and takes the form

$$\begin{aligned} \begin{array}{clc} \displaystyle \mathcal{G}_{\infty }^{(Z-1)}(u_1,\ldots ,u_N) &{} = \displaystyle \left( \sum _{j=1}^N W^{(\infty )}_ju_j\right) ^{Z-1}&{} \\ \\ &{} = \displaystyle \sum _{s_1+s_2+\cdots +s_N=Z-1} \mathcal{A}(s_1,s_2,\ldots , s_N) u_1^{s_1}u_2^{s_2} \ldots u_N^{s_N}.&{} \end{array} \end{aligned}$$

(22)

The ‘state-probabilities’ that $s_j$ susceptible walkers are on node j ($j=1,\ldots N$) with $\sum _js_j=Z-1$ then are obtained as

$$\begin{aligned} \displaystyle \mathcal{A}(s_1,s_2,\ldots , s_N)= & {} \displaystyle \frac{1}{s_1!s_2!\ldots s_N!}\frac{\partial ^{Z-1}}{\partial u_1^{s_1}\partial u_2^{s_2}\ldots \partial u_N^{s_N}} ,\quad \sum _{j=1}^Ns_j=Z-1 \nonumber \\= & {} \displaystyle \frac{(Z-1)!}{s_1!s_2!\ldots , s_N!} (W^{(\infty )}_1)^{s_1}(W^{(\infty )}_2)^{s_2}\ldots (W^{(\infty )}_N)^{s_N} \end{aligned}$$

(23)

with the stationary distribution $W^{(\infty )}_j = \frac{K_j}{N\langle K\rangle }$. Now we assume that the duration of the infection is $\tau _1 \in \mathbb {N}$ and that each walker performs jumps exactly at integer times $t \in \mathbb {N}$. Accounting for the fact that the infectious walker remains on his departure node during the time-interval [0, 1) and performs its first jump at $t=1$, then it follows that the infectious walker during his infection, i.e., within the time interval $[0,\tau _1)$ performs $\tau _1-1$ jumps where at each jump he meets susceptible walkers in the stationary distribution (23). In our calculation, we ignore the transitions of susceptible walkers to the infectious state and assume the number of susceptible walkers remains constant $Z-1$. The expected number of times $\mathcal{R}(\tau _1)$ the infectious walker meets a susceptible one within the time-interval $[0,\tau _1)$ then is obtained as (where we assume the infectious walker has departure node i and transition probabilities at time t: $\mathcal{P}^{(1)}_{ij}(t)=[{\mathbf{W}}^t]_{ij}$)

$$\begin{aligned} \begin{array}{clc} \displaystyle \mathcal{R}(\tau _1) &{} = \displaystyle \sum _{t=0}^{\tau _1-1} \sum _{j=1}^N \, \sum _{s_1+s_2+,\ldots s_N=Z-1} P_{ij}^{(1)}(t)s_j \mathcal{A}(s_1,s_2,\ldots , s_N) &{} \\ \\ &{}= \displaystyle \sum _{t=0}^{\tau _1-1} \sum _{j=1}^NP_{ij}^{(1)}(t) u_j \frac{\partial }{\partial u_j} \mathcal{G}^{(Z-1)}(u_1,\ldots ,u_N)\bigg |_{u_1=\ldots =u_N=1} &{} \\ \\ &{}= \displaystyle \sum _{t=0}^{\tau _1-1} r(t) &{} \end{array} \end{aligned}$$

(24)

where

$$\begin{aligned} \begin{array}{clc} \displaystyle r(t) &{} = \displaystyle \sum _{k=1}^N P_{ik}^{(1)}(t) u_k \frac{\partial }{\partial u_j} \left( \sum _{j=1}^N W^{(\infty )}_ju_j\right) ^{Z-1}\bigg |_{u_1=\ldots =u_N=1}&{} \\ \\ &{} = (Z-1) \sum _{j=1}^N P_{ij}^{(1)}(t)W^{(\infty )}_j. \end{array} \end{aligned}$$

(25)

The quantity r(t) indicates the expected number of susceptible walkers met by the infectious one in the time increment $\varDelta t=1$ following to his tth jump and we observe that $r(0)= (Z-1)W^{(\infty )}_i$ (as $P_{ij}(0)=\delta _{ij}$). Hence, (24) yields

$$\begin{aligned} \begin{array}{clc} \displaystyle {\hat{\mathcal{R}}}(\tau _1,i) &{}= \displaystyle (Z-1) \sum _{j=1}^N W^{(\infty )}_j \sum _{t=0}^{\tau _1-1} P_{ij}^{(1)}(t) &{} \\[3mm] &{} = \displaystyle (Z-1) \sum _{j=1}^N W^{(\infty )}_j T_{ij}^{(1)}(\tau _1) &{} \\[3mm] &{} = \displaystyle \frac{(Z-1)}{N\langle K\rangle } \sum _{j=1}^N K_j T_{ij}^{(1)}(\tau _1) \end{array} \end{aligned}$$

(26)

where $T_{ij}^{(1)}(\tau )=\sum _{t=0}^{\tau -1}P^{(1)}_{ij}(\tau )$ indicates the expected sojourn time of the infectious walker (with departure node i) on node j in a walk of $\tau -1$ time steps (i.e., in a walk of duration $[0,\tau )$). For a detailed analysis of this issue, consult [24]. For $\tau _1=0$, we have with $P_{ij}^{(1)}(0)=\delta _{ij}$ in (26) ${\hat{\mathcal{R}}}(0,i)=R_0(0)=R_e(0)= (Z-1)W^{(\infty )}_j$ which are at $t=0$ the exact values for the effective and basic reproduction numbers since per construction at $t=0$ the infectious walker meets on his departure node $r(0)=(Z-1)W^{(\infty )}_i$ susceptible walkers. We also can define a global value by averaging (26) over all departure nodes of the infectious walker, namely

$$\begin{aligned} {\hat{\mathcal{R}}}(\tau _1) = \frac{1}{N} \sum _{i=1}^N {\hat{\mathcal{R}}}(\tau _1,i) = \displaystyle \frac{(Z-1)}{N^2\langle K\rangle } \sum _{i=1}^N\sum _{j=1}^N K_j T^{(1)}_{ij}(\tau _1) \ge R_0(\tau _1). \end{aligned}$$

(27)

2.3 Regular networks

It is worthy to consider above result for regular networks, i.e., networks with constant degree $K_j=K=\langle K\rangle$ ($i=1,\ldots N$). Then, we get for (26) which coincides then with (27) the simple expression

$$\begin{aligned} \begin{array}{clc} \displaystyle {\hat{\mathcal{R}}}(\tau _1,i) = \displaystyle {\hat{\mathcal{R}}} (\tau _1) &{} = \displaystyle \frac{(Z-1)}{N} \sum _{j=1}^N {\hat{\mathcal{R}}}(\tau _1,i) &{} \\ \\ &{} = \displaystyle \frac{Z-1}{N} \sum _{t=0}^{\tau _1-1} \sum _{j=1}^NP^{(1)}_{ij}(t) \\ \\ &{} = \displaystyle \frac{(Z-1) \tau _1 }{N} = \rho _s\,\tau _1 \ge R_0(\tau _1) \end{array} \end{aligned}$$

(28)

where we have used $W^{(\infty )}_j=\frac{1}{N}$ and normalization $\sum _{j=1}^NP^{(1)}_{ij}(t)=1$ where $\rho _s=\frac{Z-1}{N}$ denotes the density of the susceptible walkers.

3 Two-dimensional model

In the previous section, we ignored the transitions between the states susceptible, infectious, and recovered. In the present section, we present numerical simulations of space-time patterns of infectious/susceptible walkers where we account for transitions between them.

3.1 The model

We consider again Z independent random walkers (particles) performing independent jumps at integer times on a two-dimensional undirected graph with $N=L^2$ nodes where $(x_i^{(n)},y_i^{(n)})$ indicate the position of walker (‘particle’) i at time n, namely

$$ 1\le x_i^{(n)}\le L, \qquad 1\le y_i^{(n)}\le L $$

where $x_i,y_i,L$ are integer numbers. Let the walkers jump according to

$$\begin{aligned} x_i^{(n+1)}= & {} x_i^{(n)} + \xi _x^{(n)} \end{aligned}$$

(29)

$$\begin{aligned} y_i^{(n+1)}= & {} y_i^{(n)} + \xi _y^{(n)}, \qquad i=1,\ldots , Z. \end{aligned}$$

(30)

Here, $\xi _{x,y}$ are equally distributed random integer numbers $\xi$ in $[-h, h]$. In our simple network, each node has $d=(2h+1)^2$ accessible neighbors, where d is the degree of a node. The velocity of each walker (mean distance in one step) is given as

$$\begin{aligned} \bar{v} = \frac{1}{2h+1}\left[ \sum _{i,j=-h}^{h}\left( i^2+j^2\right) \right] ^{1/2}. \end{aligned}$$

(31)

Let $s_i$ be the ’grade of infection’ of walker i. Due to recovery, we assume a simple linear decrease

$$\begin{aligned} s_i^{(n+1)} = s_i^{(n)} - \mu \end{aligned}$$

(32)

with $1/\mu$ as the relaxation time of healing. We define particle i as infectious at time n if $s_i^{(n)}>s_1$ and as susceptible if $s_i^{(n)}\le 0$. In the range $0< s_i^{(n)} < s_1$, we define particle i to be immune.

For infection, the following rule applies. If two particles i, j meet on the same node, i.e.,

$$ x_i^{(n)} = x_j^{(n)},\qquad y_i^{(n)} = y_j^{(n)} $$

and

$$ s_i^{(n)} > s_1,\qquad s_j^{(n)} \le 0 $$

then particle i infects particle j with a given probability P. If particle j gets infected at time-step n, we set

$$ s_j^{(n)} = 1. $$

Thus, we may identify three regions (Fig. 1):

1.:

$s_1 \le s_i \le 1$: particle i is infectious and infects particle j with probability P (duration of infectibility $\tau _1$).

2.:

$0< s_j < s_1$: particle j is immune and cannot be infected by particle i (duration of immunity $\tau _2-\tau _1$).

3.:

$s_j \le 0$: particle j is healthy (again) and can be (re)-infected.

Fig. 1

Linear decrease in s(t) after infection

From Fig. 1, the relations

$$\begin{aligned} \mu = \frac{1}{\tau _2}, \qquad s_1 = 1 - \frac{\tau _1}{\tau _2} \end{aligned}$$

(33)

follow. Here, $\tau _1$ is the time while a particle can infect another one, $\tau _2$ denotes the time where a particle is not susceptible after infection (time of infectibility plus time of immunity after recovering). The period of immunity after recovering is $\tau _2-\tau _1 \ge 0$. In the present model, we assume the characteristic times $\tau _{1,2}$ to be the same for all infected and immune particles, respectively. After the time $\tau _2$, a particle is again susceptible and can be re-infected. If $\tau _2\rightarrow \infty$, particles stay immune forever after recovering.

3.2 Reproduction numbers

The basic reproduction number $R_0$ as mentioned above is defined as the number of particles that are infected by one particle under the assumption that all other particles are healthy and susceptible. The probability for a particle to meet another one during one time increment $\varDelta t=1$ is equal to the density (where we assume $Z,N\gg 1$, see relation (28) for $\tau _1=1$)

$$\begin{aligned} \rho =\frac{Z}{N} \approx \rho _s. \end{aligned}$$

(34)

To find $R_0$, this quantity must be multiplied with the time of infectivity $\tau _1$ and with the probability of infection P to obtain

$$\begin{aligned} R_0 = \rho \tau _1 P = P {\hat{\mathcal{R}}}(\tau _1). \end{aligned}$$

(35)

This simple relation indeed is consistent with expression (28) of the previous section by introducing the probability of infection P. Given $\tau _1$ and P, $R_0$ is a constant. However, in real life due to hygiene measures P may vary considerably in time but also in space, leading to an inhomogeneously distributed $R_0$. Distance rules or lockdowns may rather restrict the mobility of the particles and can be considered by changing the velocity (31) or the connectivity of the network.

Fig. 2

Effective R-number $R_e$, relative numbers of ill $z_k=Z_k/Z$ and immune $z_I=Z_I/Z$ walkers over time. The black line denotes herd immunity, Eq. (37). Here, $P=0.4,\ K=100$ and the system oscillates in form of waves

Fig. 3

Snapshots of the patterns found for the parameters of Fig. 2. Black: susceptible, red: infectious, actively ill. The typical dynamics of a wood fire can be recognized

Fig. 4

Same as Fig. 2 but for $p=1$ and $K=200$. Now the virus may die out and the disease becomes extinct after a certain number of sweeps

Fig. 5

Snapshots of the patterns found for the parameters of Fig. 4

Fig. 6

Cluster formation for small $P=0.2$ and $h=1$, initial condition of 1000 equally distributed infectious particles (red). After $t=35000$ P was increased to $P=0.3$ and the clusters grow

Fig. 7

Number of immune and ill particles for the parameters of Fig. 6. When P is increased, the number of ill walkers grows and the disease spreads

Fig. 8

Inhomogeneity factor $f_H$ over time. When the clusters grow in size after $t=35000$, $f_H$ decreases showing homogenization of the patterns

The effective reproduction number is found by replacing the particle number in (35) by the number of those particles which are not infected or not immune

$$\begin{aligned} R_e^{(n)} = R_0\frac{Z_s^{(n)}}{Z} \end{aligned}$$

(36)

where $Z_s^{(n)}$ is the total number of particles with $s_i^{(n)}\le 0$ at time n. As long as $R_e>1$ the disease spreads and more and more particles get infected. The number of insusceptible particles is given as $Z_I^{(n)}=Z-Z_s^{(n)}$, they can be either ill or immune. In course of time, $Z_s$ and therefore $R_s$ decreases. If $R_e=1$, herd immunity is reached and from (36) one finds

$$\begin{aligned} Z_I^H = Z\;\left( 1-\frac{1}{R_0}\right) . \end{aligned}$$

(37)

From the $Z_I^{(n)}$ immune particles, $Z_k^{(n)}$ are actively ill, i.e., $s_i^{(n)}>s_1$. The relation of ill to immune particles is roughly

$$\begin{aligned} \frac{Z_k^{(n)}}{Z_I^{(n)}} = \frac{\tau _1}{\tau _2}. \end{aligned}$$

(38)

Up to here, we assumed an average (stationary) particle distribution over the nodes. However, if clusters of infected particles are formed, $Z_s$ may vary strongly in space thus this assumption does not any more hold true. For an isolated cluster in an elsewhere healthy environment, $R_e$ may be locally around one and the number of ill particles saturates due to herd immunity, where in the healthy regions $R_e$ can be much larger than one.

3.3 Results

Spatial patterns are expected if the initial distribution of infected walkers is localized (clusters). Let us assume that K particles form a cluster in the central node of the layer and that all K particles are infected:

$$\begin{aligned} x_i^{(0)} = \frac{L}{2},\quad y_i^{(0)} = \frac{L}{2},\quad s_i^{(0)} = \xi ,\quad i=1\ldots K \end{aligned}$$

(39)

with $\xi$ randomly distributed in $[s_1,1]$. The other $N-K$ particles are healthy and randomly distributed over all nodes:

$$\begin{aligned} x_i^{(0)} = \eta _x,\quad y_i^{(0)} = \eta _y,\quad s_i^{(0)} = 0,\quad i=K+1,\ldots ,N \end{aligned}$$

(40)

and $\eta _x,\ \eta _y$ as random integers in [1, L].

We present numerical solutions of the system with the fixed parameters $N=30000,\ L=1500,\ N=2.25\cdot 10^6,\ h=4,\ \tau _1=600,\ \tau _2=2400$. Figures 2 and 3 show the situation for $P=0.4$, leading to a basic R-number of $R_0=3.2$. The thin black line denotes herd immunity. For Fig. 4, P was much higher, $P=1$ and the virus dies out after some sweeps (Fig. 5).

Depending on P, but also on the mean particle velocity $\bar{v}$, different pattern scenarios can be obtained. For the case of small $\bar{v}=1.15$, corresponding to $h=1$ and small $P=0.2$ clusters are formed independently from the initial condition (Fig. 6). The clusters do not connect and large areas of the domain remain healthy. As a consequence, the average number of infected walkers stays relatively low (Fig. 7). If P or h is increased, the cluster size increases and the clusters connect (percolation point). Then, the number of infected particles increases also strongly.

To characterize cluster formation, we define an inhomogeneity factor $f_H$ that is zero if a pattern is completely homogeneous (constant) in space and that becomes large if clusters are formed. Therefore, we introduce a coarse mesh over the domain with $10\times 10$ cells and count the number of ill particles laying in each cell with $X_i$, where $i=1, \ldots , 100$. Then, we compute the normalized variance

$$\begin{aligned} f_H(X) = \frac{\langle X^2 \rangle - \langle X \rangle ^2}{\langle X^2\rangle } \end{aligned}$$

(41)

where brackets denote the average over all 100 coarse cells. Figure 8 shows $f_H$ over time for the situation plotted in Figs. 6 and 7. If clusters are formed, $f_H$ increases, but after P is increased, the clusters grow and $f_H$ tends to small values, showing that the pattern becomes more and more homogeneous.

4 Conclusions

In the present paper, we first have developed a simple Markovian random walker model of epidemic spreading in undirected graphs. We derived an upper bound for the reproduction numbers $R_0(\tau _1)$ and $R_e(\tau _1)$ in a multiple random walker model where among Z independent random walkers one is infectious and $Z-1$ are susceptible. We derived the expected number of times the infectious walker meets another (susceptible) walker (relations (26) and (27)) where this quantity constitutes an upper bound for the basic reproduction number.

Further, we performed computer simulations of the space-time evolution patterns on a 2D network. We showed that these space-time patterns depend sensitively on the infection probability P but also crucially depend on the characteristic times of infectivity $\tau _1$ and duration of immunity $\tau _2-\tau _1$ after recovering.

Despite its considerable simplicity, the present model allows predictions on the effect of lockdowns and distance rules. For future research, it would be interesting to see what happens in the space-time epidemic dynamics when $\tau _{1,2}$ become random variables drawn from waiting-time densities such as for instance exponential or Mittag-Leffler with heavy power-law tails and non-Markovian long memory features. An exponential decay in the distribution of $\tau _2-\tau _1$ describes the situation of short-time immunity whereas distributions with heavy power-law tails correspond to long-time immunity. In this way, effects of ‘genetic stability’ of a virus and its mutation activity could be taken into account. Such models could be important to obtain scenarios for the efficiency of vaccinations. Another interesting feature is introduced by the space-time fractional dynamics of the walkers on biased networks such as analyzed in recent papers [23, 25]. Although epidemic spreading has been widely addressed in many works, there are still many open questions such as effects of social distancing, lockdowns, and others calling for further thorough analysis.