Skip to main content
SpringerLink
Log in

Finite deformation analysis of isotropic magnetoactive elastomers

  • Original Article
  • Published:
Continuum Mechanics and Thermodynamics Aims and scope Submit manuscript

Abstract

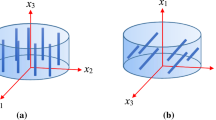
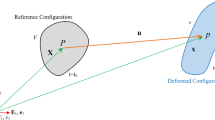
In this study, the large deformation analysis of the magnetoactive elastomers based on continuum mechanics approach has been conducted. First, the governing differential equations for the spatial configuration are presented. Stored energy density function defined with respect to the invariants of the right or left Cauchy–Green deformation tensor and the magnetic field induction vector is adopted to develop a material model for finite deformation of isotropic magnetoactive elastomers (MAEs). An isotropic magnetoactive sample with 15% iron particle volume fraction is then fabricated, and a test setup has been designed to measure its magnetic permeability. Using an advanced magnetorheometer, quasi-static tests are then carried out on MAE circular cylindrical samples to find their torque-twist response under various magnetic fields. The experimental results are then effectively utilized to identify the unknown parameters in the proposed material model. The accuracy of the proposed constitutive model in predicting the response behavior of the MAE is then demonstrated through comparison of theoretical results with those obtained experimentally.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Harvey, J.A.: Smart materials. In: Kutz, M. (ed.) Mechanical Engineers Handbook: Materials and Mechanical Design, pp. 401–418. John Wiley & Sons Inc, New Jersey (2005)

    Google Scholar 

  2. Lanotte, L., Ausanio, G., Hison, C., Iannotti, V., Luponio, C., Luponio, C.: State of the art and development trends of novel nanostructured elastomagnetic composites. J. Optoelectr. Adv. Mater. 6(2), 523–532 (2004)

    Google Scholar 

  3. Carlson, J.D., Jolly, M.R.: MR fluid, foam and elastomer devices. Mechatronics 10(4–5), 555–569 (2000)

    Google Scholar 

  4. Kallio, M.: The Elastic and Damping Properties of Magnetorheological Elastomers. VTT publications, New York (2005)

    Google Scholar 

  5. Vicente, J.D., Bossis, G., Lacis, S., Guyot, M.: Permability measurements in cobalt ferrite and carbonyl iron powders and suspensions. J. Magn. Magn. Mater. 251(1), 9 (2002)

    Google Scholar 

  6. An, Y.X., Shaw, M.T.: Actuating properties of soft gels with ordered iron particles: basis for a shear actuator. Smart Mater. Struct. 12(2), 157–163 (2003)

    ADS  Google Scholar 

  7. Lokander, M., Stenberg, B.: Improving the magnetorheological effect in isotropic magnetorheological rubber materials. Polym. Test. 22(6), 677–680 (2003)

    Google Scholar 

  8. Dishovsky, N., Ruskova, K., Radulov, I.: “In situ” magnetic modification of polar elastomers. Mater. Res. Bull. 36(1–2), 35–45 (2001)

    Google Scholar 

  9. Jolly, M.R., Carlson, J.D., Munoz, B.C.: A model of the behaviour of magnetorheological materials. Smart Mater. Struct. 5(5), 607–614 (1996)

    ADS  Google Scholar 

  10. Lokander, M., Stenberg, B.: Performance of isotropic magnetorheological rubber materials. Polym. Test. 22(3), 245–251 (2003)

    Google Scholar 

  11. Varga, Z., Filipcsei, G., Zrínyi, M.: Magnetic field sensitive functional elastomers with tuneable elastic modulus. Polymer 47(1), 227–233 (2006)

    Google Scholar 

  12. Truesdell, C., Toupin, R.: In: Flügge, S. (ed.) The Classical Field Theories, Handbuch der Physik, vol. 3.1. Springer, Berlin (1960)

  13. Toupin, R.: The elastic dielectric. J. Ration. Mech. Anal. 5(6), 849–915 (1956)

    MathSciNet  MATH  Google Scholar 

  14. Toupin, R.A.: A dynamical theory of elastic dielectrics. Int. J. Eng. Sci. 1(1), 101–126 (1963)

    MathSciNet  Google Scholar 

  15. Tiersten, H.F.: Coupled magnetomechanical equations for magnetically saturated insulators. J. Math. Phys. 5(9), 1298–1318 (1964)

    ADS  MathSciNet  MATH  Google Scholar 

  16. Tiersten, H.F.: Variational principle for saturated magnetoelastic insulators. J. Math. Phys. 6(5), 779–787 (1965)

    ADS  MathSciNet  Google Scholar 

  17. Jordan, N.F., Eringen, A.C.: On the static nonlinear theory of electromagnetic thermoelastic solids-II. Int. J. Eng. Sci. 2(1), 97–114 (1964)

    MathSciNet  MATH  Google Scholar 

  18. Maugin, G.A., Eringen, A.C.: Deformable Magnetically Saturated Media. I. Field Equations. J. Math. Phys. 13(2), 143–155 (1972)

    ADS  Google Scholar 

  19. Pao, Y.-H., Yeh, C.-S.: A linear theory for soft ferromagnetic elastic solids. Int. J. Eng. Sci. 11(4), 415–436 (1973)

    MATH  Google Scholar 

  20. Beheshti, A., Sedaghati, R., Rakheja, S.: Development of a small-deformation material model for anisotropic magneto-active elastomer. Acta. Mech. (2020). https://doi.org/10.1007/s00707-020-02647-1

    Article  MATH  Google Scholar 

  21. Pao, Y.-H.: Electromagnetic forces in deformable continua. In: Nevat-Nasser, S. (ed.) Mechanics Today, pp. 209–305. Pergamon Press Inc, New York (1978)

    Google Scholar 

  22. Tiersten, H.F., Tsai, C.F.: On the interaction of the electromagnetic field with heat conducting deformable insulators. J. Math. Phys. 13(3), 361–378 (1972)

    ADS  Google Scholar 

  23. Brown, W.F.: Magnetoelastic Interactions. Springer, Berlin (1966)

    Google Scholar 

  24. Eringen, A.C., Maugin, G.A.: Electrodynamics of Continua I Foundations and Solid Media. New York Inc. Springer, Berlin (1990)

    Google Scholar 

  25. Kovetz, A.: Electromagnet Theory. Oxford University Press, New York (2000)

    MATH  Google Scholar 

  26. Dorfmann, A., Ogden, R.W.: Magnetoelastic modelling of elastomers. Eur. J. Mech. A-Solids 22(4), 497–507 (2003)

    ADS  MathSciNet  MATH  Google Scholar 

  27. Dorfmann, A., Ogden, R.W.: Nonlinear magnetoelastic deformations. Q. J. Mech. Appl. Math. 57(4), 599–622 (2004)

    MathSciNet  MATH  Google Scholar 

  28. Dorfmann, A., Ogden, R.W.: Nonlinear magnetoelastic deformations of elastomers. Acta Mech. 167(1–2), 13–28 (2004)

    MATH  Google Scholar 

  29. Dorfmann, A., Ogden, R.W.: Some problems in nonlinear magnetoelasticity. Z. Angew, Math. Phys. 56(4), 718–745 (2005)

    MathSciNet  MATH  Google Scholar 

  30. Brigadnov, I.A., Dorfmann, A.: Mathematical modeling of magneto-sensitive elastomers. Int. J. Solids Struct. 40(18), 4659–4674 (2003)

    MATH  Google Scholar 

  31. Bustamante, R., Dorfmann, A., Ogden, R.W.: Universal relations in isotropic nonlinear magnetoelasticity. Q. J. Mech. Appl. Math. 59(3), 435–450 (2006)

    MathSciNet  MATH  Google Scholar 

  32. Bustamante, R.: Mathematical modelling of boundary conditions for magneto-sensitive elastomers: variational formulations. J. Eng. Math. 64(3), 285–301 (2008)

    MathSciNet  MATH  Google Scholar 

  33. Bustamante, R., Dorfmann, A., Ogden, R.W.: On variational formulations in nonlinear magnetoelastostatics. Math. Mech. Solids 13(8), 725–745 (2008)

    MathSciNet  MATH  Google Scholar 

  34. Bustamante, R., Ogden, R.W.: Nonlinear magnetoelastostatics: energy functionals and their second variations. Math. Mech. Solids 18(7), 760–772 (2012)

    MathSciNet  MATH  Google Scholar 

  35. Bustamante, R., Rajagopal, K.R.: Implicit constitutive relations for nonlinear magnetoelastic bodies. Proc. Math. Phys. Eng. Sci. 471(2175), 20140959 (2015)

    MathSciNet  MATH  Google Scholar 

  36. Saxena, P., Hossain, M., Steinmann, P.: Nonlinear magneto-viscoelasticity of transversally isotropic magneto-active polymers. Proc. Math. Phys. Eng. Sci. 470(2166), 20140082 (2014)

    Google Scholar 

  37. Saxena, P., Hossain, M., Steinmann, P.: A theory of finite deformation magneto-viscoelasticity. Int. J. Solids Struct. 50(24), 3886–3897 (2013)

    Google Scholar 

  38. Kankanala, S.V., Triantafyllidis, N.: On finitely strained magnetorheological elastomers. J. Mech. Phys. Solids 52(12), 2869–2908 (2004)

    ADS  MathSciNet  MATH  Google Scholar 

  39. Ericksen, J.L.: Electromagnetism in steadily rotating matter. Contin. Mech. Thermodyn. 17(5), 361–371 (2006)

    ADS  MathSciNet  MATH  Google Scholar 

  40. Batra, R.C.: Elements of Continuum Mechanics. AIAA, American Institute of Aeronautics and Astronautics, Reston, VA (2005)

    MATH  Google Scholar 

  41. Murdoch, A.I.: On criticism of the nature of objectivity in classical continuum physics. Contin. Mech. Thermodyn. 17(2), 135–148 (2005)

    ADS  MathSciNet  MATH  Google Scholar 

  42. Liu, I.S.: On Euclidean objectivity and the principle of material frame-indifference. Contin. Mech. Thermodyn. 16(1–2), 177–183 (2004)

    ADS  MathSciNet  MATH  Google Scholar 

  43. Liu, I.S.: Further remarks on Euclidean objectivity and the principle of material frame-indifference. Contin. Mech. Thermodyn. 17(2), 125–133 (2005)

    ADS  MathSciNet  MATH  Google Scholar 

  44. Gurtin, M.E., Fried, E., Anand, L.: The Mechanics and Thermodynamics of Continua. Cambridge University Press, New York (2010)

    Google Scholar 

  45. Pao, Y.-H., Hutter, K.: Electrodynamics for moving elastic solids and viscous fluids. Proc. IEEE 63(7), 1011–1021 (1975)

    MathSciNet  Google Scholar 

  46. Lopez-Pamies, O.: A new I-1-based hyperelastic model for rubber elastic materials. CR. Mécanique 338(1), 3–11 (2010)

    MathSciNet  MATH  Google Scholar 

  47. Arruda, E.M., Boyce, M.C.: A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 41(2), 389–412 (1993)

    ADS  MATH  Google Scholar 

  48. Ogden, R.W.: Large deformation isotropic elasticity—on the correlation of theory and experiment for incompressible rubberlike solids. Proc. Royal Soc. A. 326(1567), 565–584 (1972)

    ADS  MATH  Google Scholar 

Download references

Acknowledgements

Support from National Science and Engineering Research Council of Canada (NSERC)(Grant No. RGPIN/6696-2016) is gratefully acknowledged.

Author information

Authors and Affiliations

  1. Department of Mechanical, Industrial and Aerospace Engineering, Concordia University, Montreal, QC, H3G 1M8, Canada

    Alireza Beheshti, Ramin Sedaghati & Subhash Rakheja

Authors
  1. Alireza Beheshti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ramin Sedaghati
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Subhash Rakheja
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ramin Sedaghati.

Additional information

Communicated by Andreas Öchsner.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Beheshti, A., Sedaghati, R. & Rakheja, S. Finite deformation analysis of isotropic magnetoactive elastomers. Continuum Mech. Thermodyn. 33, 163–178 (2021). https://doi.org/10.1007/s00161-020-00897-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00161-020-00897-x

Keywords

Search

Navigation