Skip to main content
SpringerLink
Log in

Stochastic many-particle model for LFP electrodes

  • Original Article
  • Published:
Continuum Mechanics and Thermodynamics Aims and scope Submit manuscript

Abstract

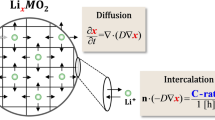
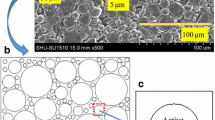
In the framework of non-equilibrium thermodynamics, we derive a new model for many-particle electrodes. The model is applied to \(\text {LiFePO}_{4}\) (LFP) electrodes consisting of many LFP particles of nanometer size. The phase transition from a lithium-poor to a lithium-rich phase within LFP electrodes is controlled by both different particle sizes and surface fluctuations leading to a system of stochastic differential equations. An explicit relation between battery voltage and current controlled by the thermodynamic state variables is derived. This voltage–current relation reveals that in thin LFP electrodes lithium intercalation from the particle surfaces into the LFP particles is the principal rate-limiting process. There are only two constant kinetic parameters in the model describing the intercalation rate and the fluctuation strength, respectively. The model correctly predicts several features of LFP electrodes, viz. the phase transition, the observed voltage plateaus, hysteresis and the rate-limiting capacity. Moreover we study the impact of both the particle size distribution and the active surface area on the voltage–charge characteristics of the electrode. Finally we carefully discuss the phase transition for varying charging/discharging rates.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

Abbreviations

U :

Reference potential \((\text {V})\)

\(k_{\text {Li}}\) :

Lithium intercalation rate \( (\text {kg}/\text {m}^2\text {s})\)

\(j_\mathtt {P}\) :

Exchange current \((\text {A}/\text {m}^2)\)

\(\nu _0\) :

Stochastic strength \((\text {m}^{\frac{3}{2}})\)

L :

Heat of solution \((\text {J})\)

\(A^i \) :

Particle surface area \((\text {m}^2)\)

\(A_\mathtt {E}^i\) :

Active surface area \((\text {m}^2)\)

\(V^i\) :

Particle volume \((\text {m}^3)\)

\(V_\mathtt {P}\) :

Total volume \((\text {m}^3)\)

\(A_\mathtt {E}\) :

Total active area \((\text {m}^2)\)

\(y^i\), \(Y^i\) :

Lithium mole fraction

\(\tau ^i\) :

Relaxation time \((\text {s})\)

\(\nu ^i\) :

Stochastic strength

\(k_\mathrm{B}\) :

Boltzmann constant \((\text {J}/\text {K})\)

\(e_0\) :

Elementary charge \((\text {C})\)

\(\varepsilon _0\) :

Electric constant \([\text {C}/(\text {V}\, \text {m})]\)

\(z_\alpha \) :

Charge number

\(m_\alpha \) :

Molecular mass \((\text {kg})\)

\(\gamma _{\alpha }^i\), \(\gamma _{\mathrm{s},\alpha }^i\) :

Stoichiometric coef. bulk and surface reactions

\(\varvec{\nu }\) :

Normal vector

\(k_M\) :

Mean curvature \((1/\text {m})\)

T,\(T_\mathrm{s}\) :

Bulk and surface temperature \((\text {K})\)

\(n_\alpha \) :

Bulk number density \((\text {m}^{-3})\)

\(n_{\mathrm{s},\alpha }\) :

Surface number density \((\text {m}^{-2})\)

\(\rho _\alpha \) :

Bulk mass density \((\text {kg}/\text {m}^{3})\)

\(\rho _{\mathrm{s},\alpha }\) :

Surface number density \((\text {kg}/\text {m}^{2})\)

\(\varvec{v}\), \(\varvec{v}_\mathrm{s}\) :

Bulk and surface barycentric velocity \((\text {m}/\text {s})\)

\(\varvec{w}\) :

Surface velocity \((\text {m}/\text {s})\)

\(\varvec{E}\) :

Electric field \((\text {V}/\text {m})\)

\(\varphi \), \(\varphi _\mathrm{s}\) :

Bulk and surface electrostatic potential \((\text {V})\)

\(n^\mathrm {F}\) :

Charge density \((\text {C}/\text {m}^3)\)

\(n^\mathrm {F}_\mathrm{s}\) :

Surface charge density \((\text {C}/\text {m}^2)\)

\(\rho \psi \) :

Free energy density \((\text {J}/\text {m}^3)\)

\(\rho _\mathrm{s}\psi _\mathrm{s}\) :

Surface free energy density \((\text {J}/\text {m}^2)\)

\(\mu _\alpha \), \(\mu _{\mathrm{s},\alpha }\) :

Bulk and surface chemical potential \((\text {J}/\text {kg})\)

\(\varvec{\sigma }\) :

Cauchy stress tensor \((\text {N}/\text {m}^2)\)

\(\varvec{\varSigma }\) :

Total stress tensor \((\text {N}/\text {m}^2)\)

p :

Material pressure \((\text {N}/\text {m}^2)\)

\(\gamma _\mathrm{s}\) :

Surface tension \((\text {N}/\text {m})\)

\(\varvec{J}_\alpha \) :

Mass flux density \((\text {kg}/\text {s}\text {m}^2)\)

\(\varvec{J}_{\mathrm{s},\alpha }\) :

Surface mass flux density \((\text {kg}/\text {s}\text {m}^2)\)

\(\varvec{j}_\alpha \) :

Total mass flux density \((\text {kg}/\text {s}\text {m}^2)\)

\(\varvec{J}_{\mathrm{s},\alpha }\) :

Surface mass flux density \((\text {kg}/\text {s}\text {m})\)

\(\varvec{j}_{\mathrm{s},\alpha }\) :

Total surface mass flux density \((\text {kg}/\text {s}\text {m})\)

\(R^i\) :

Bulk reaction rate density \((1/\text {s}\text {m}^3)\)

\(R^i_\mathrm{s}\) :

Surface reaction rate density \((1/\text {s}\text {m}^2)\)

\(r^i\) :

Bulk mass production density \((\text {kg}/\text {s}\text {m}^3)\)

\(r^i_\mathrm{s}\) :

Surface mass production density \((\text {kg}/\text {s}\text {m}^2)\)

References

  1. Bai, P., Cogswell, D., Bazant, M.: Suppression of phase separation in \(\text{ LiFePO }_4\) nanoparticles during battery discharge. Nano Lett. 11(11), 4890–4896 (2011)

    Article  ADS  Google Scholar 

  2. Bazant, M.Z.: Theory of chemical kinetics and charge transfer based on nonequilibrium thermodynamics. Acc. Chem. Res. 46(5), 1144–1160 (2013)

    Article  Google Scholar 

  3. Bedeaux, D.: Nonequilibrium thermodynamics and statistical physics of surfaces. In: Ilya, P., Rice, S.A. (eds.) Advances in Chemical Physics, pp. 47–109. Wiley, New York (1986)

    Google Scholar 

  4. Bothe, D., Dreyer, W.: Continuum thermodynamics of chemically reacting fluid mixtures. Acta Mech. 226(6), 1757–1805 (2014)

  5. Chueh, W., El Gabaly, F., Sugar, J., Bartelt, N., McDaniel, A., Fenton, K., Zavadil, K., Tyliszczak, T., Lai, W., McCarty, K.: Intercalation pathway in many-particle LiFePO\(_4\) electrode revealed by nanoscale state-of-charge mapping. Nano Lett. 13(3), 866–872 (2013)

    Article  ADS  Google Scholar 

  6. Costen, R., Adamson, D.: Three-dimensional derivation of the electrodynamic jump conditions and momentum-energy laws at a moving boundary. Proc. IEEE 53(9), 1181–1196 (1965)

    Article  Google Scholar 

  7. de Groot, S.R., Mazur, P.: Non-equilibrium Thermodynamics. North Holland, Amsterdam (1963)

    MATH  Google Scholar 

  8. Delmas, C., Maccario, M., Croguennec, L., Le Cras, F., Weill, F.: Lithium deintercalation in \(\text{ LiFePO }_4\) nanoparticles via a domino-cascade model. Nat. Mater. 7, 665–671 (2008)

    Article  ADS  Google Scholar 

  9. Dominko, R., Bele, M., Gaberšček, M., Remskar, M., Hanzel, D., Pejovnik, S., Jamnik, J.: Impact of the carbon coating thickness on the electrochemical performance of \(\text{ LiFePO }_{4}/\text{ C }\) composites. J. Electrochem. Soc. 152(3), A607–A610 (2005)

    Article  Google Scholar 

  10. Doyle, M., Fuller, T., Newman, J.: Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 140(6), 1526–1533 (1993)

    Article  Google Scholar 

  11. Doyle, M., Newman, J.: Analysis of capacity-rate data for lithium batteries using simplified models of the discharge process. J. Appl. Electrochem. 27(7), 846–856 (1997)

    Article  Google Scholar 

  12. Dreyer, W., Friz, P., Gajewski, P., Guhlke, C., Maurelli, M.: in preparation

  13. Dreyer, W., Gaberšček, M., Guhlke, C., Huth, R., Jamnik, J.: Phase transition in a rechargeable lithium battery. Eur. J. Appl. Math. 22, 267–290 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  14. Dreyer, W., Guhlke, C., Herrmann, M.: Hysteresis and phase transition in many-particle storage systems. Contin. Mech. Thermodyn. 23(3), 211–231 (2011)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. Dreyer, W., Guhlke, C., Huth, R.: The behavior of a many-particle electrode in a lithium-ion battery. Physica D 240(12), 1008–1019 (2011)

    Article  ADS  MATH  Google Scholar 

  16. Dreyer, W., Guhlke, C., Müller, R.: Overcoming the shortcomings of the Nernst–Planck model. Phys. Chem. Chem. Phys. 15, 7075–7086 (2013)

    Article  Google Scholar 

  17. Dreyer, W., Guhlke, C., Müller, R.: Modeling of electrochemical double layers in thermodynamic non-equilibrium. Phys. Chem. Chem. Phys. 17, 27176–27194 (2015)

    Article  Google Scholar 

  18. Dreyer, W., Guhlke, C., Müller, R.: A new perspective on the electron transfer: recovering the Butler-Volmer equation in non-equilibrium thermodynamics. Phys. Chem. Chem. Phys. 18, 24966–24983 (2016)

    Article  Google Scholar 

  19. Dreyer, W., Huth, R., Mielke, A., Rehberg, J., Winkler, M.: Global existence for a nonlocal and nonlinear Fokker–Planck equation. Zeitschrift für angewandte Mathematik und Physik 66(2), 293–315 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  20. Dreyer, W., Jamnik, J., Guhlke, C., Huth, R., Moškon, J., Gaberšček, M.: The thermodynamic origin of hysteresis in insertion batteries. Nat. Mater. 9, 448–453 (2010)

    Article  ADS  Google Scholar 

  21. Farkhondeh, M., Delacourt, C.: Mathematical modeling of commercial LiFePO\(_4\) electrodes based on variable solid-state diffusivity. J. Electrochem. Soc. 159(2), A177–A192 (2011)

    Article  Google Scholar 

  22. Farkhondeh, M., Pritzker, M., Fowler, M., Safari, M., Delacourt, C.: Mesoscopic modeling of li insertion in phase-separating electrode materials: application to lithium iron phosphate. Phys. Chem. Chem. Phys. 16, 22555–22565 (2014)

    Article  Google Scholar 

  23. Farkhondeh, M., Safari, M., Pritzker, M., Fowler, M., Han, T., Wang, J., Delacourt, C.: Full-range simulation of a commercial \(\text{ LiFePO }_4\) electrode accounting for bulk and surface effects: a comparative analysis. J. Electrochem. Soc. 161(3), A201–A212 (2014)

    Article  Google Scholar 

  24. Fournier, N., Hauray, M., Mischler, S.: Propagation of chaos for the 2D viscous vortex model. J. Eur. Math. Soc. (JEMS) 16(7), 1423–1466 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  25. Franco, A.: Multiscale modelling and numerical simulation of rechargeable lithium ion batteries: concepts, methods and challenges. RSC Adv. 3, 13027–13058 (2013)

    Article  Google Scholar 

  26. Guhlke, C.: Theorie der elektrochemischen Grenzfläche. Ph.D. thesis, TU-Berlin (2015)

  27. Han, B., Van der Ven, A., Morgan, D., Ceder, G.: Electrochemical modeling of intercalation processes with phase field models. Electrochim. Acta 49, 4691–4699 (2004)

    Article  Google Scholar 

  28. Hellwig, C., Sörgel, S., Bessler, W.: A multi-scale electrochemical and thermal model of a LiFePO\(_4\) battery. ECS Trans. 35(32), 215–228 (2011)

    Article  Google Scholar 

  29. Herrmann, M., Niethammer, B., Velázquez, J.: Kramers and non-Kramers phase transitions in many-particle systems with dynamical constraint. SIAM Multisc. Model. Simul. 10(3), 818–852 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  30. Herrmann, M., Niethammer, B., Velázquez, J.: Rate-independent dynamics and Kramers-type phase transitions in nonlocal Fokker–Planck equations with dynamical control. Arch. Ration. Mech. Anal. 124(3), 803–866 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  31. Latz, A., Zausch, J.: Thermodynamic consistent transport theory of Li-ion batteries. J. Power Sour. 196(6), 3296–3302 (2011)

    Article  ADS  MATH  Google Scholar 

  32. Latz, A., Zausch, J.: Thermodynamic derivation of a Butler–Volmer model for intercalation in Li-ion batteries. Electrochim. Acta 110, 358–362 (2013)

    Article  Google Scholar 

  33. Li, Y., El Gabaly, F., Ferguson, T., Smith, R., Bartelt, N., Sugar, J., Fenton, K., Cogswell, D., Kilcoyne, A., Tyliszczak, T., Bazant, M., Chueh, W.: Current-induced transition from particle-by-particle to concurrent intercalation in phase-separating battery electrodes. Nat. Mater. 13, 1476–1122 (2014)

    Google Scholar 

  34. Li, Y., Meyer, S., Lim, J., Lee, S., Gent, W., Marchesini, S., Krishnan, H., Tyliszczak, T., Shapiro, D., Kilcoyne, A., Chueh, W.: Effects of particle size, electronic connectivity, and incoherent nanoscale domains on the sequence of lithiation in LiFePO\(-4\) porous electrodes. Adv. Mater. 27(42), 6591–6597 (2015)

    Article  Google Scholar 

  35. Li, Y., Weker, J., Gent, W., Mueller, D., Lim, J., Cogswell, D., Tyliszczak, T., Chueh, W.: Dichotomy in the lithiation pathway of ellipsoidal and platelet \(\text{ LiFePO }_4\) particles revealed through nanoscale operando state-of-charge imaging. Adv. Funct. Mater. 25(24), 3677–3687 (2015)

    Article  Google Scholar 

  36. Meixner, J., Reik, H.G.: Thermodynamik der irreversiblen Prozesse, pp. 413–523. Springer, Berlin (1959)

    Google Scholar 

  37. Mielke, A., Truskinovsky, L.: From discrete visco-elasticity to continuum rate-independent plasticity: rigorous results. Arch. Ration. Mech. Anal. 203(2), 577–619 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  38. Moskon, J., Dominko, R., Cerc-Korosec, R., Gaberšček, M., Jamnik, J.: Morphology and electrical properties of conductive carbon coatings for cathode materials. J. Power Sour. 174(2), 683–688 (2007)

    Article  ADS  Google Scholar 

  39. Müller, I.: Thermodynamics, Interaction of Mechanics and Mathematics Series. Pitman Advanced Publishing Program, Boston (1985)

    Google Scholar 

  40. Padhi, A., Nanjundaswamy, K., Goodenough, J.: Phospho-olivines as positive-electrode materials for rechargeable lithium batteries. J. Electrochem. Soc. 144, 1188–1194 (1997)

    Article  Google Scholar 

  41. Safari, M., Delacourt, C.: Mathematical modeling of lithium iron phosphate electrode: galvanostatic charge/discharge and path dependence. J. Electrochem. Soc. 158(2), A63–A73 (2011)

    Article  Google Scholar 

  42. Singh, G., Ceder, G., Bazant, M.: Intercalation dynamics in rechargeable battery materials: general theory and phase-transformation waves in LiFePO\(_4\). Electrochim. Acta 53(26), 7599–7613 (2008)

    Article  Google Scholar 

  43. Srinivasan, V., Newman, J.: Discharge model for the lithium iron-phosphate electrode. J. Electrochem. Soc. 151(10), A1517–A1529 (2004)

    Article  Google Scholar 

  44. Sznitman, A.S.: Topics in propagation of chaos. In: École d’Été de Probabilités de Saint-Flour XIX—1989, Lecture Notes in Mathematics, vol. 1464, pp. 165–251. Springer, Berlin (1991)

Download references

Author information

Authors and Affiliations

  1. Weierstrass Institute, Mohrenstr. 39, 10117, Berlin, Germany

    Clemens Guhlke, Paul Gajewski & Wolfgang Dreyer

  2. Institute of Mathematics, Technische Universität Berlin, Strasse des 17. Juni 136, 10623, Berlin, Germany

    Mario Maurelli & Peter K. Friz

Authors
  1. Clemens Guhlke
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Paul Gajewski
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mario Maurelli
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Peter K. Friz
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Wolfgang Dreyer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Clemens Guhlke.

Additional information

Communicated by Andreas Öchsner.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guhlke, C., Gajewski, P., Maurelli, M. et al. Stochastic many-particle model for LFP electrodes. Continuum Mech. Thermodyn. 30, 593–628 (2018). https://doi.org/10.1007/s00161-018-0629-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00161-018-0629-7

Keywords

Search

Navigation