Abstract
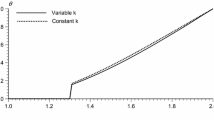
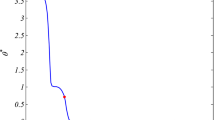
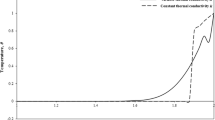
The thermoelasticity problem in a thick-walled orthotropic hollow cylinder is solved analytically using finite Hankel transform and Laplace transform. Time-dependent thermal and mechanical boundary conditions are applied on the inner and the outer surfaces of the cylinder. For solving the energy equation, the temperature itself is considered as boundary condition to be applied on both the inner and the outer surfaces of the orthotropic cylinder. Two different cases are assumed for solving the equation of motion: traction–traction problem (tractions are prescribed on both the inner and the outer surfaces) and traction–displacement (traction is prescribed on the inner surface and displacement is prescribed on the outer surface of the hollow orthotropic cylinder). Due to considering uncoupled theory, after obtaining temperature distribution, the dynamical structural problem is solved and closed-form relations are derived for radial displacement, radial and hoop stress. As a case study, exponentially decaying temperature with respect to time is prescribed on the inner surface of the cylinder and the temperature of the outer surface is considered to be zero. Owing to solving dynamical problem, the stress wave propagation and its reflections were observed after plotting the results in both cases.
Similar content being viewed by others
References
Yen, A.C., Kirmser, P.G.: On the thermal stresses in a finite circular cylinder. J. Eng. Math. 5(1), 19–32 (1971)
Kardomateas, G.A.: Thermoelastic stresses in a filament-wound orthotropic composite elliptic cylinder due to a uniform temperature change. IJSS 26(5–6), 527–537 (1990)
Shahani, A.R., Nabavi, S.M.: Analytical solution of the quasi-static thermoelasticity problem in a pressurized thick-walled cylinder subjected to transient thermal loading. Appl. Math. Model. 31(9), 1807–1818 (2007)
Shahani, A.R., Momeni Bashusqeh, S.: Analytical solution of the thermoelasticity problem in a pressurized thick-walled sphere subjected to transient thermal loading. MMS 19(2), 135–151 (2014)
Shahani, A.R., Momeni Bashusqeh, S.: Analytical solution of the coupled thermo-elasticity problem in a pressurized sphere. JThSt 36(12), 1283–1307 (2013)
Yee, K.-C., Moon, T.J.: Plane thermal stress analysis of an orthotropic cylinder subjected to an arbitrary, transient asymmetric temperature distribution. J. Appl. Mech. 69(5), 632–640 (2002)
Wang, X.: Thermal shock in a hollow cylinder caused by rapid arbitrary heating. J. Sound Vib. 183(5), 899–906 (1995)
Cho, H., Kardomateas, G.A., Valle, C.S.: Elastodynamic solution for the thermal shock stresses in an orthotropic thick cylindrical shell. J. Appl. Mech. 65(1), 184–193 (1998)
Ding, H.J., Wang, H.M., Chen, W.Q.: A solution of a non-homogeneous orthotropic cylindrical shell for axisymmetric plane strain dynamic thermoelastic problems. J. Sound Vib. 263(4), 815–829 (2003)
Jabbari, M., Dehbani, H., Eslami, M.R.: An exact solution for classic coupled thermoelasticity in cylindrical coordinates. J. Press. Vessel Technol. 133(1), 1–10 (2011)
Goshima, T., Miyao, K.: Transient thermal stresses in a hollow cylinder subjected to y-ray heating and convective heat losses. NuEnD 125(2), 267–273 (1991)
Zhang, Q., Wang, Z.W., Tang, C.Y., Hu, D.P., Liu, P.Q., Xia, L.Z.: Analytical solution of the thermo-mechanical stresses in a multilayered composite pressure vessel considering the influence of the closed ends. Int. J. Press. Vessels Pip. 98(1), 102–110 (2012)
Abd-Alla, A.M., Abd-Alla, A.N., Zeidan, N.A.: Transient thermal stresses in a transversely isotropic infinite circular cylinder. Appl. Math. Comput. 121(1), 93–122 (2001)
Kouchakzadeh, M.A., Entezari, A.: Analytical solution of classic coupled thermoelasticity problem in a rotating disk. JThSt 38(1), 1269–1291 (2015)
Shahani, A.R., Sharifi torki, H.: Analytical solution of the thermoelasticity problem in thick-walled cylinder subjected to transient thermal loading. MME 16(10), 147–154 (2016). (in Persian)
Marin, M.: On weak solutions in elasticity of dipolar bodies with voids. JCoAM 82(1–2), 291–297 (1997)
Marin, M.: Harmonic vibrations in thermoelasticity of microstretch materials. J. Vib. Acoust. 132(4), 1–6 (2010)
Sharma, K., Marin, M.: Effect of distinct conductive and thermodynamic temperatures on the reflection of plane waves in micropolar elastic half-space. U.P.B. Sci. Bull. 75(2), 121–132 (2013)
Decolon, C.: Analysis of Composite Structures. Hermes Penton Ltd, London (2002)
Rand, O., Rovenski, V.: Analytical Methods in Anisotropic Elasticity. Springer, Birkhauser Boston (2004)
Hahn, W.D., Necati O Zisik, A.: Heat Conduction, 3rd edn. Wiley, Hoboken (2012)
Sneddon, I.N.: The Use of Integral Transform. Mc-Graw-Hill Book Company, New York (1972)
Cinelli, G.: An extension of the finite hankel transform and applications. IJES 3, 539–559 (1965)
Cho, H., Kardomateas, G.A.: Thermal shock stresses due to heat convection at a bounding surface in a thick orthotropic cylinderical shell. IJSS 38, 2769–2788 (2001)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Andreas Öchsner.
Rights and permissions
About this article
Cite this article
Shahani, A.R., Sharifi Torki, H. Determination of the thermal stress wave propagation in orthotropic hollow cylinder based on classical theory of thermoelasticity. Continuum Mech. Thermodyn. 30, 509–527 (2018). https://doi.org/10.1007/s00161-017-0618-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00161-017-0618-2