Integrated statistical modeling method: part I—statistical simulations for symmetric distributions

Abstract

The use of parametric and nonparametric statistical modeling methods differs depending on data sufficiency. For sufficient data, the parametric statistical modeling method is preferred owing to its high convergence to the population distribution. Conversely, for insufficient data, the nonparametric method is preferred owing to its high flexibility and conservative modeling of the given data. However, it is difficult for users to select either a parametric or nonparametric modeling method because the adequacy of using one of these methods depends on how well the given data represent the population model, which is unknown to users. For insufficient data or limited prior information on random variables, the interval approach, which uses interval information of data or random variables, can be used. However, it is still difficult to be used in uncertainty analysis and design, owing to imprecise probabilities. In this study, to overcome this problem, an integrated statistical modeling (ISM) method, which combines the parametric, nonparametric, and interval approaches, is proposed. The ISM method uses the two-sample Kolmogorov–Smirnov (K–S) test to determine whether to use either the parametric or nonparametric method according to data sufficiency. The sequential statistical modeling (SSM) and kernel density estimation with estimated bounded data (KDE-ebd) are used as the parametric and nonparametric methods combined with the interval approach, respectively. To verify the modeling accuracy, conservativeness, and convergence of the proposed method, it is compared with the original SSM and KDE-ebd according to various sample sizes and distribution types in simulation tests. Through an engineering and reliability analysis example, it is shown that the proposed ISM method has the highest accuracy and reliability in the statistical modeling, regardless of data sufficiency. The ISM method is applicable to real engineering data and is conservative in the reliability analysis for insufficient data, unlike the SSM, and converges to an exact probability of failure more rapidly than KDE-ebd as data increase.

Appendices

Appendix 1. Probability density functions

Types	PDF	Parameters
Normal	$f\left(x|\mu, \sigma \right)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left\{\frac{-{\left(x-\mu \right)}^2}{2{\sigma}^2}\right\}$	μ: Location (mean) σ: Scale (standard deviation)
Logistic	$f\left(x|\mu, \sigma \right)=\frac{\exp \left(\frac{x-a}{b}\right)}{b{\left\{1+\exp \left(\frac{x-a}{b}\right)\right\}}^2}$	a: Location (mean) b: Scale
t Location scale	$f\left(x|\mu, \sigma, \nu \right)=\frac{\Gamma \left(\frac{\nu +1}{2}\right)}{\sigma \sqrt{\nu \pi}\Gamma \left(\frac{\nu }{2}\right)}{\left[\frac{\nu +{\left(\frac{x-\mu }{\sigma}\right)}^2}{\nu}\right]}^{-\left(\frac{\nu +1}{2}\right)}$	μ: Location (mean) σ: Scale ν: Shape

Appendix 2. Flow chart of SSM

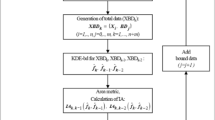
Appendix 3. Flow chart of KDE-ebd

Appendix 4. Quantile function value ratio