AK-SYSi: an improved adaptive Kriging model for system reliability analysis with multiple failure modes by a refined U learning function

Abstract

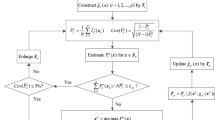
Due to multiple implicit limit state functions needed to be surrogated, adaptive Kriging model for system reliability analysis with multiple failure modes meets a big challenge in accuracy and efficiency. In order to improve the accuracy of adaptive Kriging meta-model in system reliability analysis, this paper mainly proposes an improved AK-SYS by using a refined U learning function. The improved AK-SYS updates the Kriging meta-model from the most easily identifiable failure mode among the multiple failure modes, and this strategy can avoid identifying the minimum mode or the maximum mode by the initial and the in-process Kriging meta-models and eliminate the corresponding inaccuracy propagating to the final result. By analyzing three case studies, the effectiveness and the accuracy of the proposed refined U learning function are verified.

Appendix 1. Kriging model

The Kriging model is a semi-parametric interpolation technique based on the statistical theory (Sacks et al. 1989) including the parametric linear regression part and the nonparametric stochastic process. For an unknown function g(X), the Kriging model is given as follows:

$$ \widehat{g}(X)=\sum \limits_{i=1}^q{B}_i(X){\beta}_i+Z(X)={B}^T(X)\beta +Z(X) $$

(A1)

where B(X) = [B₁(X), B₂(X), ..., B_q(X)]^T are the base functions of vector X, β = [β₁, β₂, ..., β_q]^T is the regression coefficient vector, and q denotes the number of base functions. Z(X) is a stationary Gaussian process with zero mean and covariance which can be defined as follows:

$$ \mathit{\operatorname{cov}}\left[Z\left({x}^{(i)}\right),Z\left({x}^{(j)}\right)\right]={\sigma}^2R\left(\left({x}^{(i)}\right),\left({x}^{(j)}\right)\right)\kern4.5em i,j=1,...,{N}_0 $$

(A2)

where N₀ denotes the number of training points.

Define $R=\left[\begin{array}{ccc}R\left(\left({x}^{(1)}\right),\left({x}^{(2)}\right)\right)& \dots & R\left(\left({x}^{(1)}\right),\left({x}^{\left({N}_0\right)}\right)\right)\\ {}\vdots & \ddots & \vdots \\ {}R\left(\left({x}^{\left({N}_0\right)}\right),\left({x}^{(1)}\right)\right)& \dots & R\left(\left({x}^{\left({N}_0\right)}\right),\left({x}^{\left({N}_0\right)}\right)\right)\end{array}\right]$, B is a vector of B(X) and g is corresponding vector of the limit state functions calculated at each experimental points (x⁽ⁱ⁾)(i = 1, 2, ..., N₀), the unknown β and σ² can be estimated as follows:

$$ {\displaystyle \begin{array}{l}\widehat{\beta}={\left({B}^T{R}^{-1}B\right)}^{-1}{B}^T{R}^{-1}g\\ {}\widehat{\sigma^2}=\frac{1}{N_0}{\left(g-B\widehat{\beta}\right)}^T{R}^{-1}\left(g-B\widehat{\beta}\right)\end{array}} $$

(A3)

Therefore, for any unknown point x, the Best Linear Unbiased Predictor of model $\widehat{g}(X)$ is shown to be a Gaussian random $\widehat{g}(X)\sim N\left({\mu}_{\widehat{g}}(X),{\sigma}_{\widehat{g}}(X)\right)$ where the mean and the variance are given as follows:

$$ {\displaystyle \begin{array}{l}{\mu}_g(X)={B}^T(X)\beta +{r}^T(X){R}^{-1}\left(g- B\beta \right)\\ {}{\sigma}_g^2(X)={\sigma}^2\left\{1-{r}^T(X){R}^{-1}r(X)+{\left[{B}^T{R}^{-1}r(X)-B(X)\right]}^T{\left({B}^T{R}^{-1}B\right)}^{-1}\left[{B}^T{R}^{-1}r(X)-B(X)\right]\right\}\end{array}} $$

(A4)

where ${r}^T(X)={\left[R\left((X),\left({x}^{(1)}\right)\right),...,R\left((X),\left({x}^{\left({N}_0\right)}\right)\right)\right]}^T$.