Truss topology optimization considering local buckling constraints and restrictions on intersection and overlap of bar members

Abstract

This paper illustrates the application of a two-level approximation method for truss topology optimization with local member buckling constraints and restrictions on member intersections and overlaps. Previously developed for truss topology optimization with stress and displacement constraints, that method is achieved by starting from an initial ground structure, and, combined with genetic algorithm (GA), it can handle both discrete and continuous variables, which denote the existence and cross-sectional areas of bar members respectively in the ground structure. In this work, this method is improved and extended to consider member buckling constraints and restrict intersection and overlap of members for truss topology optimization. The temporary deletion technique is adopted to temporarily remove buckling constraints when related bar members are deleted, and in order to avoid unstable designs, the validity check for truss topology configuration is conducted. By using GA to search in each possible design subset, the singularity encountered in buckling-constrained problems is remedied, and meanwhile, as the required structural analysis is replaced with explicit approximation functions in the process of executing GA, the computational cost is significantly saved. Moreover, for the consideration of restrictions on member intersecting and overlapping, the definition of such phenomena and mathematical expressions to recognize them are presented, and a new fitness function is developed to include such considerations. Numerical examples are presented to show the efficacy of the proposed techniques.

Appendices

Appendix 1: Definition of member intersecting and overlapping

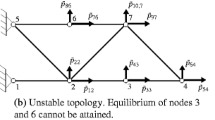
In this work, the intersection of two bars is defined as: the two bars are non-collinear and their intersectional point is inside their lengths. The schematic diagrams for the two types of intersection are shown in Fig. 17 where l₁ and l₂ represents any two bars in the truss. As for the overlap, it is defined as: the two bars are collinear, and a hinge node of one bar is located inside the length of the other bar. Likewise, the schematic diagrams for the three types of overlap are shown in Fig. 18.

Fig. 17

Schematic diagrams for intersection of two bars

Fig. 18

Schematic diagrams for overlap of two bars

For the bar nodes in Figs. 17 and 18, the hollow dots represent the normal hinge nodes, while the solid dots represent the bar nodes located inside the length of the other bar, which should be regarded as intersectional or overlapped points.

It is obvious that the intersection and overlap types defined above can include all the conditions where any two bars generate intersectional or overlapped points without physical meaning.

Appendix 2: Mathematical recognition of intersections and overlaps

Information of location coordinates for all nodes can be obtained from the structural model, and, based on the node coordinates, as shown in Fig. 19, the vectors ($\overrightarrow{a}$, $\overrightarrow{b}$, ${\overrightarrow{s}}_1$, ${\overrightarrow{s}}_2\kern0.1em$) can be constructed and used to exactly determine whether any two bars of the structure are intersecting or overlapping. Here, l_A and l_B represent any two bars with node points A₁A₂ and B₁B₂ respectively. $\overrightarrow{a}$ is a vector defined for l_A from point A₁ to point A₂, and similarly, $\overrightarrow{b}$ is a vector defined for l_B. ${\overrightarrow{s}}_1$ and ${\overrightarrow{s}}_2$ are two vectors defined from A₁ to B₁/B_2,respectively.

Fig. 19

Vectors used to determine the location relationship between two bars

Corresponding to the intersection or overlap types defined in Appendix 1, the strategy to recognize them is presented as follows:

• 1) For intersection Type-1, such relationship between two bars can be determined by the following three conditions.

• a. $\overrightarrow{a}\nparallel \overrightarrow{b}$, and the two bars are not hinge-jointed.

• b. Both hinge nodes of either bar are located beyond the length of the other bar.

• c. Values of the real number λ₁ and λ₂ exist to satisfy (24) and (25).

$$ \overrightarrow{a}={\lambda}_1{\overrightarrow{s}}_1+{\lambda}_2{\overrightarrow{s}}_2\kern0.1em $$

(24)

$$ \left\{\begin{array}{l}{\lambda}_1\ge 0\\ {}{\lambda}_2\ge 0\\ {}{\lambda}_1+{\lambda}_2>1\end{array}\right. $$

(25)

Here, (24) is a group of linear algebraic equations with respect to λ₁ and λ₂. Disassembling the vectors into their components in 3D space, these linear algebraic equations can be expressed as the (26). We can see that (26) consist of three linear algebraic equations with only two unknown variables. After solving it, one of the two conditions will appear: If (26) has no solution, the two bars are located in the different planes of the space, so they are not intersecting; if the real solutions λ₁ and λ₂ exist, i.e., two of the three equations in (26) are linear dependent, the two bars are coplanar, and when (25) is also satisfied, the two bars are intersecting with each other.

$$ \left\{\begin{array}{l}{x}_a\kern0.4em ={\lambda}_1{x}_{s1}\kern0.3em +{\lambda}_2{x}_{s2}\\ {}{y}_a={\lambda}_1{y}_{s1}+{\lambda}_2{y}_{s2}\\ {}\kern0.2em {z}_a=\kern0.5em {\lambda}_1{z}_{s1}+\kern0.5em {\lambda}_2{z}_{s2}\end{array}\right. $$

(26)

• 2) The intersection Type-2 corresponds to the following two conditions.

• a. $\overrightarrow{a}\nparallel \overrightarrow{b}$, and the two bars are not hinge-jointed.

• b. One hinge node of one bar is located inside the length of the other bar.

• 3) Corresponding to the overlap Type-1 -2 and −3, such relationships can be determined by satisfying the following two conditions.

• a. $\overrightarrow{a}\parallel \overrightarrow{b}$.

• b. One hinge node of one bar is located inside the length of the other bar.

Among the determining conditions above, the parallel relationship between the two vector $\overrightarrow{a}$ and $\overrightarrow{b}$ can be determined if (27) is satisfied, and, for example, point P is located inside the length of the bar l_A if (28) is satisfied, where the definition of ${\overrightarrow{p}}_1$, ${\overrightarrow{p}}_2$ and $\overrightarrow{a}$ can be clearly seen in Fig. 20.

$$ \left|\cos \left\langle \overrightarrow{a},\overrightarrow{b}\right\rangle \right|=\frac{\left|\overrightarrow{a}\cdot \overrightarrow{b}\right|}{\left\Vert \overrightarrow{a}\right\Vert \left\Vert \overrightarrow{b}\right\Vert }=1 $$

(27)

$$ \left\{\begin{array}{l}{\overrightarrow{p}}_1\ne \mathbf{0}\\ {}{\overrightarrow{p}}_2\ne \mathbf{0}\\ {}\left\Vert {\overrightarrow{p}}_1\right\Vert +\left\Vert {\overrightarrow{p}}_2\right\Vert =\left\Vert \overrightarrow{a}\right\Vert \end{array}\right. $$

(28)

Fig. 20

Location relationship between a point and a bar

It should be noted that, the recognition method for intersections and overlaps in this work is expressed in 3D space, and it can also be used easily in 2D truss structures only by fixing the value of one coordinate component to be a constant value, such as zero.