1 Introduction

Modern RF and microwave systems design is continuously shifting toward the use of printed circuit and surface mounted technologies to facilitate mass production and achieve compactness. Transitions are key components of microwave circuits and are used to match signals between transmission lines that have different wave impedance, propagating modes, or directions of propagation. A mismatched transition can have a significant impact on the overall system efficiency and can lead to overheating of the device.

Rectangular waveguides are commonly used to feed horn antennas (Balanis 2005, ch 13), as elements in phased array antennas (Pellegrini et al. 2014), or in material characterization (Chang et al. 1997). Meanwhile, for feeding or measurements purposes, coaxial cables are typically used to couple signals into/from waveguides. Coaxial cables support the TEM mode and possess essentially a constant characteristic impedance, whereas rectangular waveguides support TE or TM modes and have a frequency dependent wave impedance (Pozar 2012).

Coaxial-to-rectangular waveguide transitions operating over narrow frequency bands can be designed using electric probes or magnetic loops, whose configuration depends on a few parameters that are easy to determine (Keam and Williamson 1994; Deshpande et al. 1979; Bialkowski et al. 2000). However, wideband transitions typically include complex, bulky 3D structures that can be complicated to mass produce (Yi et al. 2011; Bang and Ahn 2014; Tako et al. 2014). Simeoni et al. (2006) proposed a compact type of coaxial-to-rectangular waveguide transitions that is suitable for mass production by using printed circuit board technology. However, the use of elementary design shapes together with the requirement on compactness make the proposed transitions exhibit narrow frequency band operation. Instead of relying on fixed elementary shapes when determining the layout of the printed circuit board, we will here apply the material distribution (also called density-based) technique of topology optimization to design compact wideband coaxial-to-rectangular waveguide transitions.

During the last decade, topology optimization has started to be applied to the design of various electromagnetic components, such as antennas (Nomura et al. 2007; Erentok and Sigmund 2011; Zhou et al. 2010; Aage 2011; Hassan et al. 2014b), metamaterials (Diaz and Sigmund 2010; Otomori et al. 2012), and filters (Kiziltas et al. 2004; Nomura et al. 2013; Aage and Egede Johansen 2017). As opposed to classical topology optimization approaches applied to elastic material, the layout optimization of conducting materials suffers from an ohmic barrier issue. This phenomenon stems from the fact that a material with zero (a dielectric) or infinite (a metal) conductivity exhibits no ohmic losses, in contrast to materials with intermediate conductivities. When topology optimization is applied to maximize transmission or reception, the algorithm will quickly drive each material point to either maximum or minimum conductivity values in order to minimize the losses, if no special action is taken. Moreover, it will be difficult for a continuous optimization algorithm to change a material point from metal to dielectric, or vice versa, because of the barrier of the intermediate conductivity values. Another way of expressing the same issue is to say that the problem is self-penalized toward pure dielectric–metal designs. A naive gradient-based topology optimization implementation will lead to a quick convergence of the algorithm to a lossless design, unfortunately with bad performance (Hassan et al. 2014a). This problem can be addressed by density filtering, a tool originally developed to regularize classical topology optimization problems (Bendsøe and Sigmund 2003). In previous works, we have devised a strategy for self-penalized problems based on filtering together with a continuation approach for a decreasing filter radius. We successfully applied this approach first to the design of metallic antennas (Hassan et al. 2014a, b, 2015a). A similar use of filtering as a strategy to combat the self penalization is also suggested by Aage and Egede Johansen (2017).

In the initial stage of such a strategy, when the filter radius is large, the algorithm operates on a design with large areas of material with intermediate conductivities, and as the filter radius is decreased, intermediate conductivity values are driven closer to the extreme values due to the self penalization. In the end, when the filter radius vanishes, almost all material points contain either a low or a high conductivity material. Note that in this strategy, there is no inherent size control of metal or etched areas, since the filter radius successively vanishes. Nevertheless, in a recent work, we successfully used this strategy to design the layout of metal on a printed circuit board serving as the radiating element in a coaxial-to-waveguide transition (Hassan et al. 2017). In that study, the circuit board was positioned centered and in-line with the extension of the waveguide. This position is electrically favorable, since the electric field for the dominant mode has a maximum in the center of the waveguide, and the devices we obtained indeed exhibit very wide-band operational ranges. However, the components are not compact due to the position of the circuit board.

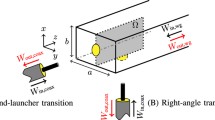
A much smaller component is accomplished by positioning the circuit board parallel and close to one end of the waveguide (see Fig. 1). This configuration is much more challenging to design, since the device is almost short circuited due to its closeness to the metallic back wall. When we attempted to design such a configuration using the continuation strategy that was successful in the in-line configuration (Hassan et al. 2017), the algorithm’s lack of control over feature sizes, both for the metallic and non-metallic (etched) parts, became apparent; the final design contained pronounced areas of scattered material and holes. Such features can increase the ohmic losses in microwave circuits, especially when appearing at the boundaries of the device (Pozar 2012, §2.7), and they can also complicate the manufacturing. It became thus necessary to improve the algorithm to control the feature size of the metallic and the non-metallic, etched parts. Here we present this improved approach, which allows the design of metal and non-metal regions with minimum-size control, and show how it has been successfully used to design compact coaxial-to-waveguide transitions. This scheme operates in two phases. The first phase aims mainly to counteract the self penalization issue by filtering the design variables using a standard linear density filter combined with a continuation approach over a successively reduced filter size—but only down to a predefined finite size corresponding to the selected feature size. The second phase uses a nonlinear filtering of the design variables, based on a sequence of parameterized harmonic mean filters (Svanberg and Svärd 2013), which in the limit yields binary designs, while at the same time maintaining the minimum feature size imposed in the first phase.

Fig. 1
figure 1

A 50-Ohm coaxial cable is connected to the rear end of an a × b rectangular waveguide. The design domain Ωis used for distributing a conductivity to match the two sides

Full size image

2 Problem statement

Figure 1 shows the problem setup. A coaxial cable is connected to one end of an a × b rectangular waveguide. In the electromagnetic community, this setup is commonly called end-launcher transition. We assume that, within the frequency band of interest, the coaxial cable supports only the TEM mode of propagation and has a constant 50 Ohm characteristic impedance. Generally, rectangular waveguides have a frequency dependent wave impedance and support different modes of propagation (Pozar 2012). In this work, the dominant TE10mode of the rectangular waveguide is considered as the mode of interest. The boundaries of the coaxial cable and the waveguide are assumed to be perfect conductors. Inside the design domain Ω, see Fig. 1, we aim to distribute material with conductivity σ to maximize the transmission of signals between the waveguide and the coaxial cable. The domain Ωis backed by a thin, low-loss dielectric substrate, occupying the volume between Ω and the shorting wall of the waveguide at z = 0, to hold the resulting conductivity distribution. The other ends of the coaxial cable and the waveguide are assumed to be matched. That is, the outgoing signals do not reflect back to the analysis domain.

3 Governing equations and discretization

The electric field E and the magnetic field H, inside the waveguide and the coaxial cable, are governed by Maxwell’s equations

$$\begin{array}{@{}rcl@{}} \partial_{t} \mu \mathbf{H} + \nabla \times \mathbf{E} &=& \mathbf{0}, \end{array} $$
(1)
$$\begin{array}{@{}rcl@{}} \partial_{t} \epsilon \mathbf{E} +\sigma \mathbf{E} - \nabla \times \mathbf{H} &=& \mathbf{0}, \end{array} $$
(2)

where μ, 𝜖, and σ are the medium permeability, permittivity, and conductivity, respectively. Under the assumption that only the TEM mode is supported by the coaxial cable, the potential difference V and the current I inside the coaxial cable satisfy the following transport equation (Hassan et al. 2014b):

$$\begin{array}{@{}rcl@{}} &&\partial_{t} (V \pm Z_{\text{c}} I ) \pm c \partial_{z} (V \pm Z_{\text{c}} I ) = 0 \ \ \ \ \ \ \forall t \text{ and} \ \forall z, \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}} &&V + Z_{\text{c}} I = g(t)\ \ \ \ \ \ \text{ at} \ z = z_{0} . \end{array} $$
(4)

Here Z cand c are the characteristic impedance and phase velocity inside the coaxial cable, respectively. The term (V + Z c I) indicates a signal traveling in the positive z-direction and is used to impose the boundary condition at the coaxial cable end z 0, and g(t)is chosen to determine the energy spectral density of the imposed signal. The term (V − Z c I)represents an outgoing signal traveling in the negative z-direction. We use this term to estimate the outgoing energy through the coaxial cable end by

$$ W_{\text{out,coax}} = \frac{1}{4 Z_{\text{c}}} {{\int}_{0}^{T}} (V - Z_{\text{c}} I)^{2} \quad dt, \qquad \text{ at}\ \ z_{0} $$
(5)

where T is the total simulation time.

We use the finite-difference time-domain (FDTD) method (Taflove and Hagness 2005) to numerically solve the governing equations (1)–(4). The computational domain is discretized by a uniform cubical Yee grid, where the conductivity is located at the edges. The incoming energy is imposed through the waveguide by the total-field scattered-field technique. The incoming energy can also be provided by specifying a nonzero function g(t) in boundary condition (4). To simulate the matched ports, the waveguide is terminated by a perfectly matched layer, and (3) together with boundary condition (4) provide perfect absorption of outgoing waves through the coaxial cable end. To control the frequency spectrum of the incoming energy, we use, as a feeding signal, a truncated time-domain sinc pulse modulated to the center of the frequency band of interest (Lathi 1998). The FDTD code is implemented to run on graphics processing units (GPUs) using the parallel computing platform CUDA (https://developer.nvidia.com/what-cuda).

4 Topology optimization problem

We first consider the case when the coaxial-to-waveguide system is fed through the waveguide by a time-domain signal that covers the frequency band of interest. For this problem we have, as illustrated in Fig. 1, the following energy balance

$$ W_{\text{in,wg}} = W_{\text{out,coax}} + W_{\text{out,wg}} + W_{\Omega}, $$
(6)

where W in,wg is the incoming energy associated with the TE10 mode imposed in the waveguide, W out,wg is the outgoing energy through the waveguide, and W Ω is ohmic losses inside the design domain Ω. To obtain a good transition between the waveguide and the coaxial cable, a natural objective is to maximize the outgoing energy through the coaxial cable, W out,coax, for the given incoming energy through the waveguide, W in,wg. According to energy balance (6), the maximization of W out,coax is equivalent to the minimization of the sum W out,wg + W Ω.

In our initial experiments for this project, and also in a previous work (Hassan et al. 2015a), we noticed that maximizing the quotient W out,coax/W out,wgusually results in optimized designs with favorable performance compared to solely maximizing W out,coax. (Maximizing W out,coax/W out,wg effectively corresponds to maximizing the transmission term W out,coaxand minimizing the reflection term W out,wg.) So, to maximize the matching between the waveguide and the coaxial cable, one possibility would be to formulate the conceptual optimization problem

$$ {\text{maximize}} \quad \log\left( \frac{W_{\text{out,coax}}}{W_{\text{out,wg}}} \right) \\ $$
(7)

subject to governing equations (1)–(4) and the boundary conditions discussed in the previous section. The performance of microwave devices is typically evaluated using the scattering parameters, which are computed as the logarithm of power ratios. Thus it is natural to use the logarithmic function in the objective function.

As mentioned in the introduction, the waveguide supports different modes of propagation and possesses a frequency dependent wave impedance. In time-domain simulations, these frequency dependencies require complicated treatments regarding the splitting of transient waves and imposing the absorbing boundary condition for the different modes in the rectangular waveguide (Kristensson 1993; Akgun and Tretyakov 2015). To circumvent these complications, we use the fact that the problem under investigation is reciprocal (Pozar 2012). That is, in problem (7), instead of observing W out,wg given an incoming energy through the waveguide, we observe W out,coaxgiven an incoming energy through the coaxial cable. We carry out two simulations, one where W in,wg is nonzero and g(t) = 0, and one where W in,wg = 0and g(t) is nonzero. Moreover, we rewrite the conceptual problem (7) as

$$ {\text{maximize}} \quad \log\left( \frac{W_{\text{out,coax}}\left|{~}_{W_{\text{in,wg}}}\right.} {W_{\text{out,coax}} \left|{~}_{W_{\text{in,coax}}}\right.} \right) \\ $$
(8)

subject to the governing equations and the boundary conditions discussed in the previous section. In problem (8), \(W_{\text {out,coax}}\left |{~}_{W_{\text {in,wg}}}\right .\) and \(W_{\text {out,coax}}\left |{~}_{W_{\text {in,coax}}}\right .\) represent the outgoing energy in the coaxial cable given the incoming energy through the waveguide and the coaxial cable, respectively. By this treatment, we are able to use the perfectly matched layer inside the waveguide to simulate a matched port that works for all modes. Moreover, because of transport equation (3), the splitting of a transient wave inside the coaxial cable is much simpler than inside the waveguide. The price for this treatment, however, is that we need to solve the governing equations twice in order to evaluate the objective function.

To solve optimization problem (8), we employ the material distribution topology optimization approach. We use a material indicator vector p = [p 1,p 2,⋯ ,p N ] to indicate presence, p i = 1, or absence, p i = 0, of the conductive material inside the design domain Ω. Our preliminary numerical experiments showed a low sensitivity of the objective function to conductivity values outside the range [σ min = 10− 3 S/m,σ max = 105 S/m]. Thus, we map the design vector p, also known as the density vector, to the physical conductivity at the edges of the design grid using

$$ \boldsymbol{\sigma} = 10^{(8 \mathbf{p}-3)} \text{S/m}. $$
(9)

To allow gradient-based optimization methods to solve optimization problem (8), the entries of the density vector are allowed to take values between 0 and 1. The topology optimization problem is to find \(\mathbf {p} \in \mathcal {A}=\{ x \in {\Bbb R}^{N} | \,\, 0 \leq x_{\text {i}} \leq 1 \quad \forall i\} \) that solves problem (8). To compute the objective function gradient, we use an adjoint-field method as detailed by Hassan et al. (2015b). The gradient vector is computed based on the solutions of two adjoint systems corresponding to the two terms \(W_{\text {out,coax}}\left |{~}_{W_{\text {in,wg}}}\right .\) and \(W_{\text {out,coax}}\left |{~}_{W_{\text {in,coax}}}\right .\) in problem formulation (8).

As mentioned in the introduction, optimization problem (8) is self-penalized toward the lossless cases (that is, toward σ min and σ max) due to the energy losses W Ωassociated with the intermediate conductivities, illustrated in Fig. 2. In other words, when gradient-based optimization methods are used to solve this problem, these methods quickly converge to designs consisting of the two extreme values of the design variables, since these values minimize the energy loss. Unfortunately, the quick convergence caused by the self penalization typically results in designs that exhibit bad performance (Hassan et al. 2014a).

Fig. 2
figure 2

A typical variation of the energy loss against the values of the design domain conductivity

Full size image

5 Filtering

Filtering procedures (Sigmund 1994; Bourdin 2001; Bruns and Tortorelli 2001) are among the most popular strategies to achieve mesh-independent designs in topology optimization. Here we consider density filtering methods, where the design variables are filtered and the filtered design variables are mapped to the coefficients that enter the governing equation. A disadvantage of the original linear density filter is that it produces designs with relatively large areas of intermediate densities. During the last decade there has been an increased interest in nonlinear filtering strategies, aimed at reducing the amount of intermediate densities (Guest et al. 2004, 2011; Sigmund 2007; Svanberg and Svärd 2013; Wadbro and Hägg 2015; Hägg and Wadbro 2017). In addition to providing mesh independent solutions, filtering of the design variables can relieve the strong self penalization discussed in the previous section. To compute the physical conductivity in expression (9), we replace the density vector p by the filtered density \(\tilde {\mathbf {p}}\) obtained by a cascade of K fW-mean filters (Wadbro and Hägg 2015),

$$ \tilde{\mathbf{p}} \stackrel{\text{def}}= \mathbf{F}^{(K)} \circ \mathbf{F}^{(K-1)} \circ {\cdots} \circ \mathbf{F}^{(1)}(\mathbf{p}), $$
(10)

where

$$ \mathbf{F}^{(k)}(\mathbf{p}) = f^{-1}_{k}(\mathbf{W}^{(k)} \, f_{k}(\mathbf{p})) \enspace\forall k \in \{1,{\cdots} , K\}, $$
(11)

and where the matrix W (k)determines the weights, shape, and the size of the k th filter; the functions f k (⋅) and their inverses \(f_{k}^{-1}(\cdot )\) are applied elementwise. The filter size is defined by a variable R that defines the radius of a circular neighborhood around each point. In this work, we use equal weights in each neighborhood. The formulation of the generalized fW-mean filter allows us to investigate different types of filters based on the choice of the functions f k (⋅). Here we employ linear as well as nonlinear filters.

5.1 Linear filter

By explicitly setting the function f k (x) = x for all k, the cascade of fW-mean filters reduces to a linear density filter. In this case, the filtering process replaces each design variable p i by a weighted arithmetic mean of the design variables within a neighborhood defined by the weight matrix W (K) W (K− 1)…W (1). The linear filter counteracts the self penalization of the optimization problem by producing designs with intermediate values.

To obtain a binary design at the end of the optimization process, we use a continuation approach over the filter radius. In particular, we start by a large filter size R max and solve a sequence of problems with decreasing filter radii, R n = γ n R max with γ < 1, until the filter radius drops below the spatial discretization step Δused in the FDTD grid. In other words, we gradually remove the impact of the filter. Unfortunately, this strategy produces mesh-dependent solutions.

5.2 Non-linear filter

To pursue nonlinear filtering of the design variables, we substitute f k (⋅) in expression (11) by harmonic functions as proposed by Svanberg and Svärd (2013) for elasticity problems. More precisely, we use functions of the form f k = (x + α)− 1 or f k = (1 − x + α)− 1. The parameter α > 0 is used to control the nonlinearity of f k (x). When α tends to infinity the harmonic filters approach a linear filter. For small values of α the harmonic filters allow for sharper transitions between regions of different materials than the linear filter. In addition, the harmonic filter operator have bounded derivatives as the nonlinearity parameter α tends to zero. We refer to the study by Svanberg and Svärd (2013) for a comprehensive comparison between the harmonic mean filters and other kinds of filters.

The f W-mean filters with the first (second) of the harmonic functions above promotes the values 0 (1), provided that the input contains 0 (1). The behavior of the two harmonic filters, for small values of α, is in this sense similar to the erode and dilate operators in mathematical morphology (Haralick et al. 1987; Heijmans 1995). On a binary design, the dilate operator dilates regions occupied with ones. That is, this operator expands areas occupied by metal. The effect of the erode operator is the opposite in the sense that it erodes regions occupied with ones; that is, it dilates regions occupied with zeros. If we cascade an erode operator followed by a dilate operator, then we get the so-called open operator that removes regions containing ones that are smaller than the neighborhood. Similarly, if we cascade a dilate operator followed by an erode operator, then we get the close operator that removes regions containing zeros that are smaller than the neighborhood.

In the numerical experiments, whenever we use non-linear filtering, we use an open–close filter; that is, an open filter followed by a close filter. The harmonic open–close filter is thus a cascade of four filters, where f 1(x) = f 4(x) = (x + α)− 1 and f 2(x) = f 3(x) = f 1(1 − x). We remark that, in general, the open-close filtering strategy does not guarantee minimum size control on both metal and etched regions, as Schevenels and Sigmund (2016) recently reported. Nevertheless, our numerical experiments suggest that the results obtained using an open–close filtering strategy in many cases provide final designs that have smooth boundaries as well as minimum size control on both the metal and etched regions.

6 Design algorithm

Figure 3 shows a summary of the proposed optimization algorithm. We start with a uniform distribution of the design variables. The first loop in the design algorithm shows the basic steps to solve a topology optimization problem. In this loop, we filter the design variables, compute the objective function and its gradient, check a convergence criterion, and then, if needed, update the design variables. As convergence criterion, we use the norm of the first-order optimality condition relative to a reference value. More precisely, we start the solution of a problem, record the norm of the first-order optimality condition after 8 iterations, continue the solution of the subproblem until the norm of the first-order optimality condition decreases to 25% of the recorded value. To update the design variables, we use the globally-convergent method of moving asymptotes (GCMMA) developed by Svanberg (2002).

Fig. 3
figure 3

The optimization algorithm including two continuation levels; one over the filter radius and one over the nonlinearity of the filter

Full size image

The second two loops in the design algorithm update the filter parameters. The first of these represents the continuation over the filter radius. In all cases, we update the filter radius using R n = max{(0.75)n × (10Δ),R min}, where we set R min = Δwhen linear filters are used. For the nonlinear filters, we investigate different values for R min. When nonlinear filters are used, the last loop represents the continuation over the nonlinearity variable α. We update the nonlinearity variable using α i = (0.5)i × α max, where α max is a starting value of α chosen to be large enough. The algorithm terminates when α i drops below α min = 10− 6. To characterize the amount of grayness in the final design, we use the non-discreteness measure, \(M_{\text {nd}} = 4\tilde {\mathbf {p}}^{T} (\mathbf {1}-\tilde {\mathbf {p}})/N\), suggested by Sigmund (2007), where N is the number of entries in \(\tilde {\mathbf {p}}\) and 1 is a vector of length N with ones at all entries. Furthermore, in a final post-processing step, we use 1 S/m as a threshold conductivity to map values below and above that value to σ min and σ max, respectively.

7 Results and discussion

We design a transition between a 50 Ohm coaxial cable and a standard WR90 rectangular waveguide. The frequency band 8–12 GHz is considered as the band of interest. The radii of the inner probe and the outer shield of the coaxial cable are 1.27 mm and 4.45 mm, respectively, and the waveguide dimensions are 22.86mm × 10.16mm. The coaxial cable is connected, to the shorting wall at the waveguide end, at a point shifted 2.54 mm in the negative x-direction from the center (see Fig. 1). We use a spatial discretization step Δ = 0.127mm in the FDTD method and a time discretization 0.95 of the Courant step. The design domain Ω, see Fig. 1, located at z = 1.27 mm, is discretized into 180 × 80cells, resulting in 28,540 design variables associated with the interior edges of the grid. The volume between z = 0 and z = 1.27 mm is filled by a low-loss RT/Duroid 5880 LZ substrate (𝜖 r = 1.96and tanδ = 0.002 at 10 GHz) to hold the design. For all design problems in this work, we start with a uniform initial distribution of the design variables, p i = 0.6, which corresponds to conductivity values near the peak in Fig. 2. This choice reduces the risk of biasing the design towards any of the two lossless cases (that is, the good dielectric and the good conductor).

7.1 Linear filter

In this section, we present the results for designing the transition using a linear filter combined with a continuation approach. First, we set the functions f k (x) = x in expression (11), and use a cascade of four linear filters (that is, K = 4in expression (10)). The reason to use the four cascaded linear filters is to obtain a filtering effect, especially in the beginning of the optimization, comparable to the one used in the next section, for the nonlinear filter. Although each filter matrix W (k) uses constant weights over a circular neighborhood of radius R, the cascade of the fW-mean filters acts as a linear filter with weighting matrix W 4 (filter size 4R) (Hägg and Wadbro 2017).

Figure 4 shows the progress of the objective function together with some snapshots showing the development of the filtered design. We include in the same figure the change in the level of non-discreteness of the filtered design. The objective function increases monotonically with distinct jumps at the beginning of each subproblem, when the filter radius decreases. At the beginning of the optimization, the design contains large amounts of intermediate values (M nd = 44%), and the boundaries are blurred, which is expected because of the large filter size. At the end of the optimization process, the design has crisp boundaries and M ndhas decreased to 1.6%.

Fig. 4
figure 4

The iteration history of the objective function and the non-discreteness level together with some samples of the filtered design. Black color indicates a good conductor and white color indicate a good dielectric

Full size image

Figure 5a shows the final conductivity distribution obtained by the optimization algorithm after 111 iterations. We note that the final design contains small metallic parts as well as small holes inside the metallic block. These small features typically appear in the design when the filter radius is reduced to small values, which indicates that the solution to the optimization problem is mesh dependent. (As we use finer grids, smaller features will likely appear in the final design.) Based on numerical investigations, these small metallic parts and holes have a minor impact on the performance of the transition. This conclusion can also be inferred from the development of the objective function in Fig. 4; there is little variation in the objective function near the end, where the small features start to appear. In practice, however, these small features may complicate the manufacturing process and raise the ohmic losses inside the transition, as mentioned in the introduction. Figure 5b shows the amplitudes of the reflection coefficient |S 11| and the coupling coefficient |S 21| of the transition. The performance of the transition is computed by our FDTD code and cross-verified with the commercial CST Microwave Studio package (https://www.cst.com/). Overall, there is a good match between the two simulations; the slight frequency shift can be accounted for by the differences in geometry description between the two methods. The optimized transition has a reflection coefficient, |S 11|, below − 8 dB and coupling coefficient, |S 21|, above − 1dB over the frequency band 8.5–12 GHz, which essentially covers the frequency band of interest marked by the vertically dashed lines in the plot. The simulation results of the transition show that there is a resonance around 11.5 GHz, which also appears, unfortunately, in many of the subsequent optimization results. We emphasize that the formulation of the objective function as the integral of the outgoing energy in time-domain makes it difficult to target a specific single frequency. We believe that this resonance is promoted by some geometrical features in the problem setup and leave this issue for future investigations.

Fig. 5
figure 5

a The final conductivity distribution over the design domain when a linear filter combined with a continuation over the filter radius is used. b The scattering parameters of the transition

Full size image

We note that the final designs may be asymmetric with respect to the symmetry plane y = a/2 (see Fig. 1). Although the problem setup is symmetric, an optimal design need not be symmetric. In fact, imposing symmetry would restrict the design space, which potentially leads to designs with poorer performance. Here, the asymmetry stems from the use of finite precision arithmetic; although the initial design conductivity is symmetric, the numerically computed fields will generally not be perfectly symmetric. Given asymmetric design conductivities, the optimization algorithm may drive the design back to the symmetric case or away from it depending on the design sensitivities.

To further improve the performance of the transition, we use an additional design layer inside the waveguide at the plane z = 2.54mm to distribute the conductivity. The new design domain consists of two layers, one layer at z = 1.27 mm and the second layer at z = 2.54mm, with a low-loss RT/Duroid 5880 LZ substrate filling the volume between z = 0 mm and z = 2.54 mm. The new design problem has 57,080 design variables and is solved using the same settings as the one-layer design case. Figure 6a and b show the final design obtained after 92 iterations. We note the appearance of small metallic parts in the second layer at z = 2.54mm. These small features, as mentioned for the one-layer design, appear when the filter size diminishes, since the solution of the optimization problem becomes mesh dependent. The non-discreteness level of the final design is M nd = 0.3%. Figure 6c shows the improvement in the performance of the two-layer design compared to Fig. 5b. The |S 11| curve has values below − 12.5 dB over the frequency band 8.4–12 GHz with a corresponding |S 21|above − 0.5dB, excluding the resonance around 11 GHz.

Fig. 6
figure 6

Results of optimizing the two-layer design using the linear filtering approach. a First layer conductivity distribution, z = 1.27mm. b Second layer conductivity distribution, z = 2.54mm. c The scattering parameters of the transition

Full size image

To conclude, the approach used in this section has the drawback that small features can appear in the final designs, as shown in Figs. 5a and 6b. These features appear as a consequence of reducing the filter radius during the continuation approach. These small features can increase the ohmic losses (Pozar 2012, §2.7) and cause manufacturing problems.

7.2 Nonlinear filters

In this section, we present the results when using the proposed two-phase filtering approach. We use a cascade of four fW-mean filters to implement the open–close filter discussed in Section 5. In a one dimensional test problem, we noticed only small differences between filtered designs obtained by using values of α > 8in the harmonic open–close (fW-mean) filter and the case when a linear filter is used (that is, when f k (x) = x for all k). Therefore, in the first phase of the filtering process, Phase I, we fix the nonlinearity variable α to α max = 8, and we follow a continuation approach over the filter radius, as in the case of the linear filter. That is, we solve a sequence of problems, for which the the filter radius is updated using R n = (0.75)n × (10Δ). Here, the filter radius is updated until the radius reaches a specified value R min ∈{3Δ,5Δ,7Δ}. In the second phase of the filtering process, Phase II, we fix the filter radius to R min and start a continuation approach over the nonlinearity variable α aiming for binary solutions. In Phase II, we update the nonlinearity variable using α i = (0.5)i × (8), and the algorithm stops when α i drops below 10− 6. We remark that if the required final filter size R minis large, then Phase I only has a minor influence, since the harmonic open–close (fW-mean) filter performs similar to a linear filter in the beginning of Phase II. However, in our numerical experiments, we noticed that generally the use of the two-phase filtering approach allows the algorithm to converge to better solutions in terms of the objective function. In particular, Phase I is essential to obtain good results when a small R min is used.

Figure 7 shows the progress of the objective function and the non-discreteness level of the filtered design for the one-layer design case using the two-phase filtering approach, when R min = 3Δis used. The optimization algorithm converged to the final solution after 330 iterations (100%), of which 49 iterations (15%) are used in Phase I and 281 iterations (85%) are used in Phase II. By the end of Phase I, the objective function increased to 88% of the maximum value and the level of non-discreteness decreased to 15%(from an initial value of 44%). In Phase II, the change in the objective function is relatively smaller than that in Phase I, nevertheless, it is essential to carefully update the nonlinearity variable α to avoid numerical instabilities in the continuation approach. The design algorithm converged to a final design with M nd = 1.0%.

Fig. 7
figure 7

The objective function and non-discreteness level of the physical design, when we use the two-phase filtering approach to design the one-layer transition

Full size image

Figure 8a shows the final design for the case R min = 3Δ, with the small circle included above the figure indicating the filter size. We note that, except for the staircasing inherited intrinsically in the FDTD discretiziation, the use of the open–close filter removed both the metallic (black color) and the dielectric (white color) features smaller than the filter size. The performance of the transition, given in Fig. 8b, is essentially the same as the one obtained by the linear filter.

Fig. 8
figure 8

a The final conductivity distribution over the one-layer design domain, when we use the two-phase filtering approach with \(R_{\min }= 3 {\Delta }\). b The scattering parameters of the transition

Full size image

To illustrate the effect of the parameter R min, we present two additional designs obtained by the design algorithm for R min = 5Δ and R min = 7Δ, in Figs. 9 and 10, which were obtained after 336 and 296 iterations with a final M nd = 0.7% and M nd = 1.5%, respectively.

Fig. 9
figure 9

a The final conductivity distribution over the one-layer design domain, when we use the two-phase filtering approach with \(R_{\min }= 5{\Delta }\). b The scattering parameters of the transition

Full size image
Fig. 10
figure 10

a The final conductivity distribution over the one-layer design domain, when we use the two-phase filtering approach with \(R_{\min }= 7 {\Delta }\). b The scattering parameters of the transition

Full size image

To obtain a quantitative measure of the size control in the final designs, we estimate their minimum sizes by seeking the largest R so that for any edge e in the design there exists a circle C e with radius R that contains e and is inscribed in the design. We estimate the minimum size of the metallic parts as well as the dielectric protrusions in the final designs. The estimated minimum sizes for the metallic parts of the designs in Figs. 8a, 9a, and 10a are 3Δ, 6Δ, and 7Δ, respectively. The corresponding dielectric protrusions have estimated minimum sizes 3Δ, 5Δ, and 7Δ, respectively. Therefore, we may conclude that the use of the open–close filter imposes minimum size control over the metallic parts as well as the dielectric protrusions, with minor impact on the performance compared to the results obtained with the linear filter.

Similar to the linear filter case, we use the proposed nonlinear filtering to investigate the design of a two-layer transition. Figures 11, 12, and 13 show the optimization results obtained by the algorithm when we use R min = 3Δ, R min = 5Δ, and R min = 7Δ, respectively. These results were obtained by the design algorithm after 334, 350, and 316 iterations with final M nd of 0.3%, 0.3%, and 0.9%, respectively. The effect of the filter radius R minis more prominent on the second layer of the designs in Figs. 11b, 12b, and 13b, where we see that the small features in the final design have a size comparable to the corresponding value of R min. The estimated minimum size of the first layer’s metallic parts are 6Δ, 11Δ, and 8Δ for the designs in Figs. 11a, 12a, and 13a, respectively, while the metallic parts in the second layer (Figs. 11b, 12b, and 13b) have estimated minimum sizes 3Δ, 5Δ, and 7Δ, respectively. The dielectric protrusions in both layers in Figs. 11, 12, and 13 have estimated minimum size 3Δ, 5Δ, and 7Δ, respectively. That is, in all cases and for both the metallic and dielctric parts the estimated minimum sizes are greater than or equal to the employed filter radii. Overall, the use of the open–close filter imposed minimum size control over the features of the designs with minor impact on design performance.

Fig. 11
figure 11

Results of optimizing the two-layer design by using the two-phase filtering approach with \(R_{\min }= 3 {\Delta }\). a First layer conductivity distribution, z = 1.27mm. b Second layer conductivity distribution, z = 2.54mm. c The scattering parameters of the transition

Full size image
Fig. 12
figure 12

Results of optimizing the two-layer design by using the two-phase filtering approach with \(R_{\min }= 5 {\Delta }\). a First layer conductivity distribution, z = 1.27mm. b Second layer conductivity distribution, z = 2.54mm. c The scattering parameters of the transition

Full size image
Fig. 13
figure 13

Results of optimizing the two-layer design by using the two-phase filtering approach with \(R_{\min }= 7 {\Delta }\). a First layer conductivity distribution, z = 1.27mm. b Second layer conductivity distribution, z = 2.54mm. c The scattering parameters of the transition

Full size image

8 Conclusion

The filtering of the design variables is essential to counteract the self penalization of the optimization problem and to avoid designs with poor performance. The simplest use of filtering, that is, a linear filter combined with a continuation approach over the filter radius, makes it possible to combat the self penalization issue; however, undesirable small features sometimes appear in the final design. To control the size of the small features in the design, we propose a two-phase filtering approach, based on a cascade of fW-mean filters. The numerical experiments, cross-verified with a commercial solver, indicate that the proposed filtering approach makes it possible to impose minimum size control with minor impact on the performance of the designs.