Abstract
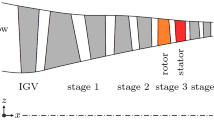
Multidisciplinary Design Optimization (MDO) method has been widely investigated and applied in the aircraft engine design. In the conceptual and preliminary design phase of the aircraft engine turbine MDO, automatic modeling and mesh generation of the blend between the blade and the shroud are two key technologies. A robust algorithm should be able to perform well without the target recognition of the geometric feature of the blend. A strategy of hexahedral mesh regeneration based on the Topological Homeomorphism is presented in this paper, where improved parametric modeling can be obtained for the turbine blade and disk. The optimal solutions of low pressure turbine of an aircraft engine could be obtained to examine the feasibility and availability of automatic modeling and mesh regeneration. The simulation results demonstrate that the proposed method is capable of satisfying the requirement on material strength by optimizing the blade blend radius, where the total weight of blade and disk can be reduced by 5.882%.








Similar content being viewed by others
References
Altair (2017) Hyperworks desktop,version 2017.0 64-bit. http://www.altairhyperworks.com/product/HyperMesh/
Alves M, Fernandes J, Rodrigues J, Martins P (2003) Finite element remeshing in metal forming using hexahedral elements. J Mater Process Technol 141(3):395–403
ANSYS (2013) Ansys inc products, ansys icem cfd,version 15.0 64-bit
ANSYShelp (2013) Ansys help viewer 15.0, ansys documentation, icem cfd totorials documentation
Benzley SE, Perry E, Merkley K, Clark B, Sjaardama G (1995) A comparison of all hexagonal and all tetrahedral finite element meshes for elastic and elasto-plastic analysis. In: Proceedings, 4th International Meshing Roundtable, Sandia National Laboratories Albuquerque, NM, vol 17, pp 179–191
Berci M, Toropov V, Hewson R, Gaskell P (2014) Multidisciplinary multifidelity optimisation of a flexible wing aerofoil with reference to a small uav. Struct Multidiscip Optim 50(4):683–699
Calvo NA, Idelsohn SR (2002) All-hexahedral element meshing: automatic elimination of self-intersecting dual lines. Int J Numer Methods Eng 55(12):1439–1449
Cass RJ, Benzley SE, Meyers RJ, Blacker TD (1996) Generalized 3-d paving: an automated quadrilateral surface mesh generation algorithm. Int J Numer Methods Eng 39(9):1475–1489
Dassault (2015) Dassault systemes, isight, simulia execution engine, verison 5.9.4. https://www.3ds.com/products-services/simulia/products/isight-simulia-execution-engine//
ESIsoftware (2013) Esi advanced cfd,version 2013.0 64-bit. https://www.esi-group.com/software-solutions/virtual-environment/cfd-multiphysics/ace-suite/cfd-geom/
Francois B, Stephen M, Jasmin T (2009) Preliminary multi-disciplinary optimization (pmdo) an example at engine level. Technical report, RTO-EN-AVT-167
Gu C-Z, Wu XY (2008) A review of fem and trend of development. Comput Sci Technol 2(3):248–259
Joe B (1994) Tetrahedral mesh generation in polyhedral regions based on convex polyhedron decompositions. Int J Numer Methods Eng 37(4):693–713
Junior HAEO, Ingber L, Petraglia A, Petraglia MR, Machado MAS (2012) Adaptive simulated annealing. Springer, Berlin
Lai M, Benzley SE, Sjaardema G, Tautges T (1996) A multiple source and target sweeping method for generating all hexahedral finite element meshes. In: Proceedings International Meshing Roundtable, pp 217–225
Li T, McKeag R, Armstrong C (1995) Hexahedral meshing using midpoint subdivision and integer programming. Comput Methods Appl Mech Eng 124(1-2):171–193
Long D (2014) Aeroengine overall multidisciplinary design optimization research based on flow path. Master’s thesis, Beijing University of Aeronautics and Astronautics, Beijing
Ming-wu L, Benzley SE, Sjaardema G, Tautges T (1996) A multiple source and target sweeping method for generating all-hexahedral finite element meshes. In: Proceedings, 5th International Meshing Roundtable, Citeseer, vol 96, pp 217–225
Mitchell SA (1999) The all-hex geode-template for conforming a diced tetrahedral mesh to any diced hexahedral mesh. Eng Comput 15(3):228–235
Nagendra S, Staubach J, Suydam A, Ghunakikar S, Akula V (2005) Optimal rapid multidisciplinary response networks: Rapiddisk. Struct Multidiscip Optim 29(3):213–231
Panchenko V, Moustapha H, Mah S, Patel K, Dowhan M (2003) Preliminary multi-disciplinary optimization in turbomachinery design. Technical report, DTIC Document
Park C, Haftka RT, Kim NH (2017) Remarks on multi-fidelity surrogates. Struct Multidiscip Optim 55 (3):1029–1050
Price MA, Armstrong CG, Sabin M (1995) Hexahedral mesh generation by medial surface subdivision: Part i. solids with convex edges. Int J Numer Methods Eng 38(19):3335–3359
RMnukres J (2004) Topology, 2nd edn. English. China Machine Press, China
Sampath R, Plybon R, Meyers C, Irani R, Balasubramaniam M (2004) High fidelity system simulation of aerospace vehicles using npss. In: 42nd AIAA Aerospace Sciences Meeting and Exhibit, p 371
Schneiders R (1996) A grid-based algorithm for the generation of hexahedral element meshes. Eng Comput 12(3-4):168–177
Shen XL, Long D (2014) Research on multidisciplinary design optimization of aeroengine turbine flow path in the preliminary design phase. In: ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, American Society of Mechanical Engineers, pp V02BT45A009–V02BT45A009
Siemens PLM (2012) Unigraphics nx, verison 8.5. http://www.plm.automation.siemens.com/en/products/nx/about-nx-software.shtml/
Staten ML, Canann SA, Owen SJ (1999) Bmsweep: locating interior nodes during sweeping. Eng Comput 15(3):212–218
Tautges TJ (2001) The generation of hexahedral meshes for assembly geometry: survey and progress. Int J Numer Methods Eng 50(12):2617–2642
Wang RQ, Jia J, Fan J, Hu D, Shen XL (2011) Hexahedral mesh regeneration method for mdo on complex aero-engine components. J Aerosp Power 9(26):2032–2038
Xiao G (2001) Aero engine design manual, fifth volume: turojet and turbofan engine overall design. Aviation Industry Press, China
Yu KH, Yue ZF, Wang J (2007) Parametric modeling and multidisciplinary design optimization of 3-d internally cooled turbine blades. In: 7th AIAA ATIO Conference, 2nd CEIAT International Conference on Innovation and Integration in Aero Sciences, 17th LTA Systems Technical Conference; followed by 2nd TEOS Forum, p 7719
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Shen, X., Hu, W. & Fan, J. Automatic blade blend modeling and hexahedral mesh regeneration for aircraft engine optimization. Struct Multidisc Optim 57, 1345–1355 (2018). https://doi.org/10.1007/s00158-017-1816-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-017-1816-z