Skip to main content
SpringerLink
Log in

An intelligent sampling approach for metamodel-based multi-objective optimization with guidance of the adaptive weighted-sum method

  • RESEARCH PAPER
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

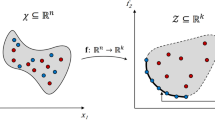
In order to reduce the computational cost of multi-objective optimization (MOO) with expensive black-box simulation models, an intelligent sampling approach (ISA) is proposed with the guidance of the adaptive weighted-sum method (AWS) to construct a metamodel for MOO gradually. The initial metamodel is built by using radial basis function (RBF) with Latin Hypercube Sampling (LHS) to distribute samples over the design space. An adaptive weighted-sum method is then employed to obtain the Pareto Frontier (POF) efficiently based on the metamodel constructed. The design variables related to extreme points on the frontier and an extra point interpolated between the maximal-minimal-distance point along the frontier and the nearest boundary point are selected as the concerned points to update the metamodel, which could improve the metamodel accuracy gradually. This iterative updating strategy is performed until the optimization problem is converged. A series of representative mathematical examples are systematically investigated to demonstrate the effectiveness of the proposed method, and finally it is employed for the design of a bus body frame.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  • Buhmann MD (2004) Radial basis functions. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  • Carlos AC, Gregorio TP, Maximino SL (2004) Handling multiple objectives with particle swarm optimization. IEEE T Evolut Comput 8:256–279

    Article  Google Scholar 

  • Chen GD, Han X, Liu GP, Jiang C, Zhao ZH (2012) An efficient multiobjective optimization method for black-box functions using sequential approximate technique. Appl Soft Comput 12(1):14–27

    Article  Google Scholar 

  • Chen SK, Xiong Y, Chen W (2009) Multiresponse and Multistage Metamodeling Approach for Design Optimization. AIAA J 47(1):206–218

    Article  Google Scholar 

  • Chen SS, Jiang Z, Yang SX, Chen W (2017) Multimodel Fusion Based Sequential Optimization. AIAA J 55(1):241–254

    Article  Google Scholar 

  • Chen ZZ, Peng SP, Li XK, Qiu HB, Xiong HD, Gao L, Li PG (2015) An important boundary sampling method for reliability-based design optimization using kriging model. Struct Multidiscip Optim 52(1):55–70

    Article  MathSciNet  Google Scholar 

  • Cox DD, John S (1997) SDO: a statistical method for global optimization. In: Alexandrov N, Hussaini MY (eds) Multidisciplinary Design Optimization: State of the Art. SIAM, Philadelphia, pp 315–329

    Google Scholar 

  • Dai HZ, Zhao W, Wang W, Cao ZG (2011) An improved radial basis function network for structural reliability analysis. J Mech Sci Technol 25(9):2151–2159

    Article  Google Scholar 

  • Das I, Dennis JE (1998) Normal-boundary intersection: a new method for generating pareto optimal points in multicriteria optimization problems. SIAM J Optim 8:631–657

    Article  MathSciNet  MATH  Google Scholar 

  • Fang JG, Gao YK, An XZ, Sun GY, Chen JN, Li Q (2016) Design of Transversely-Graded Foam and Wall Thickness Structures for Crashworthiness Criteria. Compos Part B-Eng 92:338–349

    Article  Google Scholar 

  • Fang JG, Sun GY, Qiu N, Kim NH, Li Q (2017b) On design optimization for structural crashworthiness and its state of the art. Struct Multidiscip Optim 55:1091–1119

    Article  MathSciNet  Google Scholar 

  • Fang JG, Gao YK, Sun GY, Zheng G, Li Q (2015) Dynamic crashing behavior of new extrudable multi-cell tubes with a functionally graded thickness. Int J Mech Sci 103:63–73

    Article  Google Scholar 

  • Fang J, Qiu N, An X, Xiong F, Sun G, Li Q (2017a) Crashworthiness design of a steel-aluminum hybrid rail using multi-response objective-oriented sequential optimization. Adv Eng Softw. https://doi.org/10.1016/j.advengsoft.2017.05.013

  • Forrester AIJ, Keane AJ (2009) Recent advances in surrogate-based optimization. Prog Aerosp Sci 45(1–3):50–79

    Article  Google Scholar 

  • Jin R, Chen W, Simpson TW (2001) Comparative studies of metamodelling techniques under multiple modelling criteria. Struct Multidiscip Optim 23(1):1–13

    Article  Google Scholar 

  • Jones D (2001) A taxonomy of global optimization methods based on response surfaces. J. Global Optim 21:345–383

    Article  MathSciNet  MATH  Google Scholar 

  • Kim IY, de Weck OL (2004) Adaptive weighted-sum method for bi-objective optimization: Pareto front generation. Struct Multidiscip Optim 29(2):149–158

    Article  Google Scholar 

  • Kim IY, de Weck OL (2006) Adaptive weighted sum method for multiobjective optimization: a new method for Pareto front generation. Struct Multidiscip Optim 32(2):105–116

    Article  MathSciNet  MATH  Google Scholar 

  • Lee Y, Oh S, Choi DH (2008) Design optimization using support vector regression. J Mech Sci Technol 22(2):213–220

    Article  Google Scholar 

  • Li EY, Wang H, Ye F (2016) Two-level Multi-surrogate Assisted Optimization method for highdimensional nonlinear problems. Appl Soft Comput 46:26–36

    Article  Google Scholar 

  • Lin C, Gao FL, Bai YC (2017) Multiobjective reliability-based design optimisation for front structure of an electric vehicle using hybrid metamodel accuracy improvement strategy-based probabilistic sufficiency factor method. Int J Crashworthines. https://doi.org/10.1080/13588265.2017.1317466

  • Lin C, Gao FL, Wang WW, Chen XK (2016) Multi-objective optimization design for a battery pack of electric vehicle with surrogate models. J Vibroeng 18(4):2343–2358

    Article  Google Scholar 

  • Lin QZ, Li JQDZH, Chen JY, Ming Z (2015) A novel multi-objective particle swarm optimization with multiple search strategies. Eur J Oper Res 247(3):732–744

    Article  MathSciNet  MATH  Google Scholar 

  • Liu HT, Xu SL, Ma Y, Chen XD, Wang XF (2016) An adaptive bayesian sequential sampling approach for global metamodeling. J Mech Design 138(1):011404

    Article  Google Scholar 

  • Messac A, Ismail-Yahaya A, Mattson CA (2003) The normalized normal constraint method for generating the pareto frontier. Struct Multidiscip Optim 25:86–98

    Article  MathSciNet  MATH  Google Scholar 

  • Messac A, Mullur A (2008) A computationally efficient metamodeling approach for expensive multiobjective optimization. Optim Eng 9(1):37–67

    Article  MathSciNet  Google Scholar 

  • Morteza K, Hirotaka S, Keiichi M (2015) Simulation-based design optimisation to develop a lightweight body-in-white structure focusing on dynamic and static stiffness. Int. J Vehicle Des 67:219–236

    Article  Google Scholar 

  • Murugan P, Kannan S, Baskar S (2009) NSGA-II algorithm for multi-objective generation expansion planning problem. Electr Power Syst Res 79(4):622–628

    Article  Google Scholar 

  • Nedjah N, Mourelle LD (2015) Evolutionary multi-objective optimisation: a survey. Int J Bio-Inspir Com 7:1–25

    Article  Google Scholar 

  • Preuss M, Naujoks B, Rudolph G (2006) Pareto set and EMOA behavior for simple multimodal multiobjective functions. Lecture Notes in Computer Science 4193:513–522

  • Stuckman BE (1988) A global search method for optimizing nonlinear systems. IEEE Trans Syst Man Cybernet 18(6):965–977

    Article  MathSciNet  MATH  Google Scholar 

  • Schonlau M (1998) Computer experiments and global optimization. University of Waterloo, Waterloo

    Google Scholar 

  • Su YX, Chi R (2017) Multi-objective particle swarm-differential evolution algorithm. Neural Comput & Applic 28:407–418

    Article  Google Scholar 

  • Sun GY, Li GY, Zhou SW, Li HZ, Hou SJ, Li Q (2011) Crashworthiness design of vehicle by using multiobjective robust optimization. Struct Multidiscip Optim 44(1):99–110

    Article  Google Scholar 

  • Sun ZL, Wang J, Li R, Tong C (2017) LIF: A new Kriging based learning function and its application to structural reliability analysis. Reliab Eng Syst Saf 157:152–265

    Article  Google Scholar 

  • Wang C, Duan QY, Gong W, Ye AZ, Di ZH, Miao CY (2014) An evaluation of adaptive surrogate modeling based optimization with two benchmark problems. Environ Model Softw 60:167–179

    Article  Google Scholar 

  • Wang GG, Shan S (2004) Design space reduction for multi-objective optimization and robust design optimization problems. SAE Trans 113:101–110

  • Wang H, Li EY, Li GY (2009) The least square support vector regression coupled with parallel sampling scheme metamodelling technique and application in sheet forming optimization. Mater Des 30(5):1468–1479

    Article  MathSciNet  Google Scholar 

  • Wang H, Li GY, Li EY (2010) Time-based metamodeling technique for vehicle crashworthiness optimization. Comput Method Appl M 199(37–40):2497–2509

    Article  MATH  Google Scholar 

  • Wang H, Yao LG, Hua ZZ (2008) Optimization of sheet metal forming processes by adaptive response surface based on intelligent sampling method. J Mater Process Technol 197(1–3):77–88

    Google Scholar 

  • Wang H, Ye F, Chen L, Li EY (2017) Sheet metal forming optimization by using surrogate modeling techniques. Chin J Mech Eng-En 30(1):22–36

    Article  Google Scholar 

  • Xiao YY, Yin HF, Fang HB, Wen GL (2016) Crashworthiness design of horsetail-bionic thin-walled structures under axial dynamic loading. Int J Mech Mater Des 12:563–576

    Article  Google Scholar 

  • Yang BS, Yeun YS, Ruy WS (2002) Managing approximation models in multiobjective optimization. Struct Multidiscip Optim 24(2):141–156

    Article  Google Scholar 

  • Ye F, Wang H, Li GY (2017) Variable stiffness composite material design by using support vector regression assisted efficient global optimization method. Struct Multidiscip Optim 56(1):203–219

    Article  Google Scholar 

  • Yun Y, Yoon M, Nakayama H (2009) Multi-objective optimization based on metamodeling by using support vector regression. Optim Eng 10(2):167–181

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang MC, Gou WX, Li L, Yang F, Yue ZF (2017a) Multidisciplinary design and multi-objective optimization on guide fins of twin-web disk using Kriging surrogate model. Struct Multidiscip Optim 55:361–373

    Article  Google Scholar 

  • Zhong W, Su RY, Gui LJ, Fan ZJ (2016) Multi-objective topology and sizing optimization of bus body frame. Struct Multidiscip Optim 54(3):701–714

    Article  Google Scholar 

  • Zhang Y, Gong DW, Cheng J (2017b) Multi-objective particle swarm optimization approach for cost-based feature selection in classification. IEEE ACM T Comput BI 14:64–75

    Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (NO. 51575044), the Science and Technology Planning Project of Beijing City (NO. Z161100001416007) and the National Key R&D Program of China (NO. 2017YFB0103801).

Author information

Authors and Affiliations

  1. National Engineering Laboratory for Electric Vehicles, School of Mechanical Engineering, Beijing Institute of Technology, Beijing, 100081, China

    Cheng Lin, Fengling Gao & Yingchun Bai

  2. Collaborative Innovation Center of Electric Vehicles in Beijing, Beijing Institute of Technology, Beijing, 100081, China

    Cheng Lin, Fengling Gao & Yingchun Bai

Authors
  1. Cheng Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fengling Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yingchun Bai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yingchun Bai.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lin, C., Gao, F. & Bai, Y. An intelligent sampling approach for metamodel-based multi-objective optimization with guidance of the adaptive weighted-sum method. Struct Multidisc Optim 57, 1047–1060 (2018). https://doi.org/10.1007/s00158-017-1793-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-017-1793-2

Keywords

Search

Navigation