Skip to main content
SpringerLink
Log in

Multi-model reliability-based design optimization of structures considering the intact configuration and several partial collapses

  • RESEARCH PAPER
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

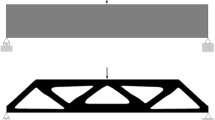
Some structures require keeping a specific safety level even if part of their elements have collapsed. The aim of this paper is to obtain the optimum design of these structures when uncertainty in some parameters that affects to the structural response is also considered. A Reliability-Based Design Optimization (RBDO) problem is formulated in order to minimize the mass of the structure fulfilling probabilistic constraints in both intact and damaged configurations. The proposed methodology combines the formulation of multi-model optimization with RBDO techniques programmed in a Matlab code. Two application examples are presented consisting of a two-dimensional truss structure with stress constraints as well as a curved stiffened panel of an aircraft fuselage subjected to buckling constraints.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  • Abaqus (2014) Abaqus 6.14.2. Documentation

  • Altair OptiStruct (2013) User Manual Version 12. Altair Engineering Inc, Detroit

    Google Scholar 

  • Aoues Y, Chanteauneuf A (2010) Benchmark study of numerical methods for reliability-based design optimization. Struct Multidiscip Optim 41(2):277–294

    Article  MathSciNet  MATH  Google Scholar 

  • Baldomir A, Hernández S, Romera LE, Díaz J (2012) Size optimization of shell structures considering several incomplete configurations. 8th AIAA multidisciplinary design optimization specialist conference, Sheraton Waikiki Honolulu, Hawaii

  • Baldomir A, Kusano I, Hernandez S, Jurado JA (2013) A reliability study for the Messina bridge with respect to flutter phenomena considering uncertainties in experimental and numerical data. Comput Struct 128:91–100

    Article  Google Scholar 

  • Baldomir A, Tembrás E, Hernández S (2015) Optimization of cable weight in multi-span cable- stayed bridges. Application to the forth replacement crossing. proceedings of multi-span large bridges

  • Choi SK, Grandhi RV, Canfield R, Pettit CL (2004) Polynomial chaos expansion with latin hypercube sampling for estimating response variability. AIAA J 42(6):1191–1198

    Article  Google Scholar 

  • Choi S-K, Grandhi RV, Canfield RA (2007) Reliability-based structural design. Springer-Verlag, London

    MATH  Google Scholar 

  • Cid Montoya M, Costas M, Díaz J, Romera LE, Hernández S (2015) A multi-objective reliability-based optimization of the crashworthiness of a metallic-GFRP impact absorber using hybrid approximations. Struct Multidiscip Optim 52(4):827–843

    Article  Google Scholar 

  • Cornell CA (1969) A probability based structural code. JAm Concr Inst 66(12):974–985

    Google Scholar 

  • D’Ippolito R, Ito K, van der Heggen B, Tzannetakis N (2012) Probabilistic optimization of the transmission loss of a composite ribbed panel. 25th international conference on noise and vibration engineering, ISMA2012 in conjunction with the 4th international conference on Uncertainty in Structural Dynamics, USD 2012; Leuven; Belgium, Code 107115

  • Du X, Chen W (2004) Sequential optimization and reliability assessment method for efficient probabilistic design. J Mech Des 126(2):225–233

    Article  Google Scholar 

  • Enevoldsen I, Sørensen JD (1994) Reliability-based optimization in structural engineering. Struct Saf 15(3):169–196

    Article  Google Scholar 

  • Eurocode 9 (2007) Design of all aluminum structures, Part 1-1: General Common rules, BS EN 1999-1-1

  • Hasofer AM, Lind NC (1974) Exact and invariant second-moment code format. J Eng Mech Div ASCE 100(1):111–121

    Google Scholar 

  • Hu Z, Li H, Du X (2013) Simulation-based time-dependent reliability analysis for composite hydrokinetic turbine blades. Struct Multidiscip Optim 47:765–781

    Article  Google Scholar 

  • Jansen M, Lombaert G, Schevenels M, Sigmund O (2014) Topology optimization of fail-safe structures using a simplified local damage model. Struct Multidiscip Optim 49(4):657–666

    Article  MathSciNet  Google Scholar 

  • Kusano I, Baldomir A, Jurado JA, Hernández S (2014) Reliability based design optimization of long-span bridges considering flutter. J Wind Eng Ind Aerodyn 135:149–162

    Article  Google Scholar 

  • Kusano I, Baldomir A, Jurado JA, Hernández S (2015) Probabilistic optimization of the main cable and bridge deck of long-span suspension bridges under flutter constraint. J Wind Eng Ind Aerodyn 146:59–70

    Article  Google Scholar 

  • López C, Bacarreza O, Baldomir A, Hernández S (2016) Reliability-based design optimization of composite stiffened panels in post-buckling regime. Struct Multidiscip Optim 55(3):1121-1141

  • MATLAB (2013) Matlab R2013a documentation

  • Moustapha M, Sudret B, Bourinet J-M, Guillaume B (2016) Quantile-based optimization under uncertainties using adaptive Kriging surrogate models. Struct Multidiscip Optim 54(6):1403-1421

  • Pedersen P (1972) On the optimal layout of multi-purpose trusses. Comput Struct 2:695–712

    Article  Google Scholar 

  • Post-Tensioning Institute (2007) Recommendations for stay cable design, testing and installation, 5th Edition, Phoenix, AZ

  • Saad L, Aissani A, Chateauneuf A, Raphael W (2016) Reliability-based optimization of direct and indirect LCC of RC bridge elements under coupled fatigue-corrosion deterioration processes. Eng Fail Anal 59:570–587

    Article  Google Scholar 

  • Tu J, Choi KK, Park YH (1999) A new study on reliability-based design optimization. J Mech Des Trans ASME 121(4):557–564

    Article  Google Scholar 

  • U.S. Department of Transportation (2000) Minimizing the hazards from propeller blade and hub failures. Federal Aviation Administration, Advisory Circular, AC 25.905–1

  • U.S. Department of Transportation (2011) Damage tolerance and fatigue evaluation of structure. Federal Aviation Administration, Advisory Circular, AC 25.571–1D

  • Wu YT (1994) Computational methods for efficient structural reliability and reliability sensitivity analysis. AIAA J 32(8):1717–1723

    Article  MATH  Google Scholar 

  • Wu YT, Millwater HR, Cruse TA (1990) Advanced probabilistic structural analysis method for implicit performance functions. AIAA J 28(9):1663–1669

    Article  Google Scholar 

  • Young YL, Baker JW, Motley MR (2010) Reliability-based design and optimization of adaptive marine structures. Compos Struct 92(2):244–253

    Article  Google Scholar 

  • Zhao YG, Ono T (2001) Moment methods for structural reliability. Struct Saf 23(1):47–75

    Article  Google Scholar 

  • Zhou M, Fleury R (2016) Fail-safe topology optimization. Struct Multidiscip Optim 54(5):1225–1243

    Article  Google Scholar 

Download references

Acknowledgements

The research leading to these results is part of the research project DPI2016-76934-R financed by the Spanish Ministry of Economy and Competitiveness.

Author information

Authors and Affiliations

  1. Structural Mechanics Group, School of Civil Engineering, Universidade da Coruña, Campus de Elviña s/n, 15071, A Coruña, Spain

    Clara Cid Bengoa, Aitor Baldomir, Santiago Hernández & Luis Romera

Authors
  1. Clara Cid Bengoa
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Aitor Baldomir
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Santiago Hernández
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Luis Romera
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Clara Cid Bengoa.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cid Bengoa, C., Baldomir, A., Hernández, S. et al. Multi-model reliability-based design optimization of structures considering the intact configuration and several partial collapses. Struct Multidisc Optim 57, 977–994 (2018). https://doi.org/10.1007/s00158-017-1789-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-017-1789-y

Keywords

Search

Navigation