Multivariate High-Order Attacks of Shuffled Tables Recomputation

Abstract

Masking schemes based on tables recomputation are classical countermeasures against high-order side-channel attacks. Still, they are known to be attackable at order d in the case the masking involves d shares. In this work, we mathematically show that an attack of order strictly greater than d can be more successful than an attack at order d. To do so, we leverage the idea presented by Tunstall, Whitnall and Oswald at FSE 2013: We exhibit attacks which exploit the multiple leakages linked to one mask during the recomputation of tables. Specifically, regarding first-order table recomputation, improved by a shuffled execution, we show that there is a window of opportunity, in terms of noise variance, where a novel highly multivariate third-order attack is more efficient than a classical bivariate second-order attack. Moreover, we show on the example of the high-order secure table computation presented by Coron at EUROCRYPT 2014 that the window of opportunity enlarges linearly with the security order d. These results extend that of the CHES ’15 eponymous paper. Here, we also investigate the case of degree one leakage models and formally show that the Hamming weight model is the less favorable to the attacker. Eventually, we validate our attack on a real ATMEL smartcard.

1 Introduction

For more than 16 years now, side-channel attacks (SCA [17]) have been a threat against cryptographic algorithms in embedded systems. To protect cryptographic implementations against these attacks, several countermeasures have been developed. Data masking schemes [14] are widely used since their security can be formally grounded.

The rationale of masking schemes goes as follows: each sensitive variable is randomly splitted in d shares (using $d-1$ masks), in such a way that any tuple of $d-1$ shares manipulated during the masked algorithm is independent from any sensitive variable. Masking schemes are the target of higher-order SCA [5, 25, 31]. A dth-order attack combines the leakages of d shares. In the implementation of masking schemes, it is particularly challenging to compute nonlinear parts of the algorithm, such as for example the S-Box of AES (a function from n bits to n bits). To solve this difficulty, different methods have been proposed which can be classified in three categories [19].

• Algebraic methods [2, 26]. The outputs of the S-Box will be computed using the algebraic representation of the S-Box.

• Global look-up table [24, 29] method. A table is precomputed off-line for each possible input and output masks.

• Table recomputation methods which precompute a masked S-Box stored in a table [1, 5, 20]. Here, the full table is recomputed despite not all entries will be called. Such tables can be recomputed only once per encryption to reach first-order security. More recently, Coron presented at EUROCRYPT 2014 [7] a table recomputation scheme secure against dth-order attacks. Since this countermeasure aims at high-order security ($d>1$), it requires one full table precomputation before every S-Box call.

These methods provide security against differential power analysis [18] (DPA) or higher-order DPA (HODPA). Still, whatever the protection order, there is at least one leakage associated to each share; in practice, shares (typically masks) can leak more than once. For example, attacks exploiting the multiplicity of leakages of the same mask during the table recomputation have been presented by Pan et al. [23] and more recently by Tunstall et al. [30]. Such attacks consist in guessing the mask in a first-order horizontal correlation power analysis [3, 10] (CPA) and then conducting a first-order vertical CPA knowing the mask. We refer to these attacks as Horizontal–Vertical attacks (HV attacks).

Shuffling the table recomputation makes the HV attacks more difficult. Still shuffling can be bypassed if the random permutation is generated from a seed with low entropy, since both the mask and the shuffling seed can be guessed [30].

Our contributions. Our first contribution is to describe a new HODPA tailored to target the table recomputation despite a highly entropic masking (unexploitable by exhaustive search). More precisely, we propose an innovative combination function, which has the specificity to be highly multivariate. We relate attacks based on the combination function of state-of-the-art and our new HODPA attack to their success rate, which allows for a straightforward comparison.

We build a theoretical analysis of their success rate. Our analysis reveals that there is a window of opportunity, when the noise variance is smaller than a threshold, where our new HODPA is more successful than a straightforward HODPA, despite it being higher order. Specifically, our analysis allows to derive mathematically that the previously known attacks require up to three times more traces than our new attack to extract the key. In addition, the impact of the leakage functions (Hamming weight, weighted sum of bits, etc.) is identified, and as a consequence the best and the worst cases for our new attack are found.

For instance, in this paper we attack a first-order masking scheme based on table recomputation with a ($2^{n+1}+1$)-variate third-order attack more efficiently than with a classical bivariate second-order attack. In this case, HV attacks could not be applied. This is the first time that a nonminimal-order attack is proved better (in terms of success rate) than the attack of minimal order. Actually, this nonintuitive result arises from a relevant selection of leaking samples—this question is seldom addressed in the side-channel literature. We generalize our attack to a higher-order masking scheme based on tables recomputation (Coron, EUROCRYPT 2014) and prove that it remains better than a classical attack, with a window of opportunity that actually grows linearly with the masking-order d.

Finally, we propose a new innovative countermeasure in order to protect masking schemes based on tables recomputation against our new attack.

Outline of the paper. The rest of the paper is organized as follows. Section 2 introduces the notations used in this article. Section 3 provides a reminder on table recomputation algorithms and on the way to defeat and protect this algorithm using random permutations. In Sect. 4, we propose a new attack against the “protected” implementation of the table recomputation, prove theoretically the soundness of the attack and validate these results by simulation. In Sect. 5, we apply this attack on a higher-order masking scheme. Section 6 extends our results to the case where the leakage function is affine in the bits of the targeted sensitive variable. In Sect. 7, we validate our results on real traces. Finally in Sect. 8, we present a countermeasure to mitigate the impact of our new attack.

2 Preliminary and Notations

In this article, capital letters (e.g., U) denote random variables and lowercase letters denote their realizations (e.g., u).

Let $k^{\star }$ be the secret key of the cryptographic algorithm. T denotes the input or the ciphertext. We suppose that the computations are done on n-bit words which means that these words can be seen as elements of $\mathbb {F}_2^n$. As a consequence both $k^{\star }$ and T belong to $\mathbb {F}_2^n$. Moreover, as we study protected implementations of cryptographic algorithms these algorithms also take as input a set of uniform independent random variables (not known by an attacker). Let denote by $\mathcal {R}$ this set.

Let g be a mapping which maps the input data to a sensitive variable. A sensitive variable is an internal variable proceeded by the cryptographic algorithm which depends on a subset of the inputs not known by the attacker (e.g., the secret key but also the secret random value). A measured leakage is modeled by:

$$\begin{aligned} X = \varPsi \left( g \left( k^{\star } , T, \mathcal {R} \right) \right) + N , \end{aligned}$$

(1)

where $\varPsi : \mathbb {F}_2^n \rightarrow \mathbb {R}$ denotes the leakage function. This leakage function is a specific characteristic of the target device. The leakage function could be for example the Hamming Weight (denoted by $\mathsf {HW}$ in this article), or a weighted sum of bits (investigated in greater details in Sect. 6). The random variable N denotes an independent additive noise. In order to conduct a dth-order attack, an attacker should combine the leakages of d shares. To combine these leakages, an attacker will use a combination function [5, 21, 22]. The degree of this combination function must be at least d for the attack to succeed. The combination function will then be applied both on the measured leakages and on the model (this is the optimal HODPA). As a consequence, an HODPA is completely defined by the combination function used.

In the rest of the paper, the ${\text {SNR}}$ is given by the following definition:

Definition 1

(Signal-to-noise ratio) The signal-to-noise ratio of a leakage denoted by a random variable L depending on informative part denoted I is given by:

(2)

An attack is said sound when it allows to recover the key $k^{\star }$ with success probability which tends to one when the number of measurements tends to the infinity.

3 Masking Scheme with Table Recomputation

3.1 Algorithm

In this article, we consider Boolean masking schemes. In particular, we focus on schemes based on table recomputation where the masked S-Box is stored in a table and fully recomputed each time.

This algorithm begins by a key addition phase where one word of the plaintext t, one word the key $k^\star$ and a random mask word m, are Xored together.

Then, these values are passed through a nonlinear function (stored in a table). The output of this operation can be masked by a different mask $m^{\prime }$. Some linear operations can follow the nonlinear function. Of course, in the whole algorithm, all the data are masked (exclusive-ored) with a random mask, to ensure the protection against first-order attacks.

Masking the linear parts is straightforward but passing through the nonlinear one is less obvious. To realize this operation, the table is recomputed. For all the elements of $\mathbb {F}_2^n$, the input mask is removed and then the output is masked by the output mask. In this step, the key is never manipulated so all the leakages concern the mask. It can also be noticed that a new table $S^{\prime }$ of size $2^n \times n$ bits is required for this step.

3.2 Classical Attacks

As any masking scheme, table recomputation can be defeated without the leakage of the table recomputation. Indeed, an attacker can use:

• Second-order attacks [5] such as second-order CPA (${\text {2O-CPA}}$). It can be noticed that for such attacks, the adversary can also exploit the leakage of the mask during the table recomputation.

• Collisions attacks. If several S-Boxes are masked by the same mask the Collisions attacks may be practicable [6].

However, these attacks do not take into account all the leakages due to table recomputation stage. An approach to exploit these leakages is to combine all of them with a leakage depending on the key. This method has been presented in [30] where an “horizontal” attack is performed on the table recomputation to recover the mask.

In such “horizontal” attacks, two different steps can be targeted:

• An attacker could try to recover the output masks. In this case, he should first recover the address in the table. In this case, it is not necessary to recover the input mask but only the address value.

• An attacker could also try to recover the input masks.

The second step consists in a vertical attack which recover the key. In this second step, the mask is now a known value. It can be noticed that the exact knowledge of the mask is not required to recover the key. Indeed, if the probability to recover the mask is higher than $\frac{1}{2^n}$, then a first-order attack is possible (because the mask distribution is biased).

Recently, the optimal distinguisher in the case of masking has been studied in [4]: it is applied to the precomputation phase of masked table without shuffling in Sect. 5. This attack can be extended to the case of shuffled table recomputation but would require an enumeration of all shuffles, which is computationally unfeasible.

3.3 Classical Countermeasure

The strategy to protect the table recomputation against HV attacks and the distinguisher presented in [4] is to shuffle the recomputation, i.e., do the recomputation in a random order, as illustrated in Algorithm 1.

Different methods to randomize the order are presented in [30]. One of the methods presented is based on a random permutation on a subset of $\mathbb {F}_2^n$.

Let $S_{2^n}$ the symmetric group of $2^n$ elements, which represents all the ways to shuffle the set $\{0,\ldots ,2^n-1\}$. If the random permutation over $\mathbb {F}_2^n$ is randomly drawn from a set of permutation $S\subset S_{2^n}$, where $card\left( S \right) \ll card\left( S_{2^n} \right)$, it is still possible for an attacker to take advantage of the table recomputation. Indeed, as it is shown in [30] attacks could be built by including all the possible permutations alongside with the key hypothesis. If the permutation is drawn uniformly over the $S_{2^n}$, the number of added hypothesis is $2^n!$ which can be too much for attacks. For instance, for $n=8$, we have $2^8!\approx 2^{1684}$.

By generating a highly entropic permutation, such as defined in [30] or any pseudorandom permutation generator (RC4 key scheduler$\ldots$), a designer could protect table recomputation against HV attacks. Indeed, using for example five or six bytes of entropy as seed for the permutation generator could be enough to prevent an attacker from guessing all the possible permutations.

4 Totally Random Permutation and Attack

In this section, we present a new attack against shuffled table recomputation. The success of this attack will not be impacted by the entropy used to generate the shuffle. As a consequence, this attack will succeed when the HV attacks will fail because the quantity of entropy used to generate the shuffle is too large to be exhaustively enumerated. We then express the condition where this attack will outperform the state-of-the-art second-order attack.

4.1 Defeating the Countermeasure

As the permutation $\varphi$ is completely random, the value of the current index in the for loop (line 3 to line 7) is unknown. But it can be noticed that this current index $\varvec{\varphi (\omega )}$, printed in boldface for clarity, is manipulated twice at each step of the loop (line 4, line 5):

$$\begin{aligned}&z \leftarrow \varvec{\varphi (\omega )} \oplus m, \end{aligned}$$

(3)

$$\begin{aligned}&z^{\prime } \leftarrow S[ \varvec{\varphi (\omega )}]\oplus m^{\prime }. \end{aligned}$$

(4)

Let U a random variable uniformly drawn over $\mathbb {F}_2^n$ and $m \in \mathbb {F}_2^n$ a constant. Then, it is shown in [25] that:

$$\begin{aligned} \mathbb {E}\left[ \left( \mathsf {HW}[U ] - \mathbb {E}\left[ \mathsf {HW}[U ] \right] \right) \times \left( \mathsf {HW}[U\oplus m ] - \mathbb {E}\left[ \mathsf {HW}[U \oplus m ] \right] \right) \right] = -\frac{\mathsf {HW}[m ]}{2} + \frac{n}{4} . \end{aligned}$$

(5)

As a consequence, it may be possible for an attacker to exploit the leakage depending on the two manipulations [Eqs. (3) and (4)] of the current random index in the loop. Indeed, at each of the $2^n$ steps of the loop in the table recomputation, the leakage of the $\varvec{\varphi (\omega )}$ in Eqs. (3) and (4) which plays the role of U in Eq. (5) will be combined (by a centered product) to recover a variable depending on the mask. Afterward, these $2^n$ variables will be combined together (by a sum) in order to increase the SNR as much as possible. Finally, this sum is combined (again by a centered product) with a leakage depending on the key. This rough idea of the attack is illustrated on Fig. 1, which represents the “trace” corresponding to the dynamic execution of Algorithm 1, followed by the masked AES AddRoundKey and SubBytes steps.

Fig. 1

State-of-the-art attack and new attack investigated in this article

Remark 1

(Construction of the high-order attack) The construction of the attack depicted in Fig. 1 leverages on two building blocks:

• 1. the centered product, represented as

  

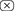
  , which allows to get rid of a mask [recall Eq. (5)], albeit at the expense of a smaller SNR (it is squared, as shown in [11]—see Sec. 4.3)

• 2. the sum of variables with the same leakage model, represented as

  

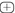
  , which increases the SNR linearly with the number of variables summed together.

An attacker could want to perform the attack on the output of the S-Box. But depending on the implementation of the masking scheme, the output masks can be different for each address of the S-Box (see for example the masking scheme of Coron [7]). To avoid loss of generality, we focus our study on the S-Box input mask of the recomputation. Indeed, by design of the table recomputation masking scheme, the input mask is the same for each address of the S-Box: The attacker can thus exploit it multiple times. Moreover, an attacker can still take advantage of the confusion of the S-Box [13] to better discriminate the various key candidates. Indeed, he can target the input the of SubBytes operation of the last round. Notice the use of capital M and capital $\varPhi$, which indicates that the leakage is modeled as a random variable.

4.2 Multivariate Attacks Against Table Recomputation

In the previous section, it has been shown that at each iteration of the loop of the table recomputation, it is possible to extract a value depending on the mask. As a consequence, it is possible to use all of these values to perform a multivariate attack. In this subsection, we give the formal formula of this new attack. Let us define the leakages of the table recomputation. The leakage of the masked random index in the loop is given by: $\mathsf {HW}[ \varPhi \left( \omega \right) \oplus M ] + N_{\omega }^{(1)}$. The leakage of the random index is given by: $\mathsf {HW}[\varPhi \left( \omega \right) ] + N_{\omega }^{(2)}$.

Depending on the knowledge about the model, the leakage could be centered by the “true” expectation or by the estimation of this expectation. We assume this expectation is a known value given by: $\mathbb {E}\left[\mathsf {HW}[\varPhi \left( \omega \right) \oplus M ] + N_{\omega }^{(1)} \right] = \mathbb {E}\left[\mathsf {HW}[\varPhi \left( \omega \right) ] + N_{\omega }^{(2)} \right] = \frac{n}{2}$. Then, let us denote the central leakages as:

$$\begin{aligned} X_{\omega }^{(1)}&= \mathsf {HW}[\varPhi \left( \omega \right) \oplus M ] + N_{\omega }^{(1)} -\frac{n}{2}, \end{aligned}$$

(6)

$$\begin{aligned} X_{\omega }^{(2)}&= \mathsf {HW}[\varPhi \left( \omega \right) ] + N_{\omega }^{(2)}-\frac{n}{2}. \end{aligned}$$

(7)

Besides, the leakage of the masked AddRoundKey is:

$$\begin{aligned} X^{\star } = \mathsf {HW}[T \oplus M \oplus k^{\star } ] + N -\frac{n}{2}. \end{aligned}$$

(8)

In a view to use all the leakages of the table recomputation, an original combination function could be defined.

Definition 2

The combination function ${\text {C}}_{TR}$ exploiting the leakage of the table recomputation is given by:

$$\begin{aligned} \begin{array}{cccc} {\text {C}}_{TR}:&{} \mathbb {R}^{2^{n+1}} \times \mathbb {R}&{} \longrightarrow &{} \mathbb {R}\\ &{} \left( \left( X_{\omega }^{(1)}, X_{\omega }^{(2)} \right) _{0\leqslant \omega \leqslant 2^n-1} , X^{\star } \right) &{} \longmapsto &{} \left( -2 \times \frac{1}{2^n} \sum _{\omega = 0}^{2^n-1} X_{\omega }^{(1)} \times X_{\omega }^{(2)} \right) \times X^{\star } . \end{array} \end{aligned}$$

Following Fig. 1, it can be noticed that ${\text {C}}_{TR}$ is in fact the combination of two sub-combination functions. Indeed, first of all, the leakages of the table recomputation are combined; the result of this combination is the following value:

$$\begin{aligned} X_{TR}=-2 \times \frac{1}{2^n} \sum _{\omega = 0}^{2^n-1} X_{\omega }^{(1)} \times X_{\omega }^{(2)}. \end{aligned}$$

(9)

Second, this value is multiplicatively combined with $X^{\star }$.

Remark 2

It can be noticed that the random variable $X_{TR}$ does not depend on $\varPhi$. Indeed in Eq. (9), the sum can be reordered by $\varPhi$. Moreover, as this sum is computed over all the possible $\varPhi \left( \omega \right)$ it implies that $\frac{1}{2^n} \sum _{\omega = 0}^{2^n-1} X_{\omega }^{(1)} \times X_{\omega }^{(2)}$ is exactly the expectation over the $\varPhi \left( \omega \right)$. As a consequence, $X_{TR}$ is random only through the mask and the noise.

Based on the combination function ${\text {C}}_{TR}$, a multivariate attack can be built.

Definition 3

The multivariate attack (MVA) exploiting the leakage of the table recomputation (TR) is given by the function:

$$\begin{aligned} \begin{array}{cccc} {\text {MVA}}_{TR}:&{} \mathbb {R}^{2^{n+1}} \times \mathbb {R}\times \mathbb {R}&{} \longrightarrow &{} \mathbb {F}_2^n \\ &{} \left( \left( X_{\omega }^{(1)}, X_{\omega }^{(2)} \right) _{\omega } , X^{\star } , Y \right) &{} \longmapsto &{} \displaystyle \mathop {{{\mathrm{argmax}}}}\limits _{k \in \mathbb {F}_2^n} \mathsf {\rho }\left[{\text {C}}_{TR}\left( \left( X_{\omega }^{(1)}, X_{\omega }^{(2)} \right) _{\omega } , X^{\star } \right) , Y \right] , \end{array} \end{aligned}$$

where $Y=\mathbb {E}\left[\left( \mathsf {HW}[T \oplus M \oplus k ] - \frac{n}{2} \right) \cdot \left( \mathsf {HW}[M ] - \frac{n}{2} \right) | T \right]$ and $\rho$ is the Pearson coefficient. According to Eq. (5), the model Y is equal to an affine transformation of $-\mathsf {HW}[T\oplus k ]$ (note the negative sign for the correlation $\rho$ extremal value when $k \in \mathbb {F}_2^n$ to be positive).

Proposition 1

${\text {MVA}}_{TR}$ is sound.

Proof

By the law of large numbers, correlation coefficient involved in the expression of ${\text {MVA}}_{TR}$ tends to $\rho (-\mathsf {HW}[T\oplus k^* ], -\mathsf {HW}[T\oplus k ])$ when the number of traces tends to infinity. This quantity is maximal when $k=k^*$, by the Cauchy–Schwarz theorem. Then, for enough traces the noise will impact all the key guesses similarly and as a consequence the result of ${\text {MVA}}_{TR}$ is maximal when $k=k^*$. $\square$

Remark 3

The attack presented in Definition 3 is a $(2^{n+1}+1)$-multivariate third-order attack.

Let us denote the leakage of the mask (which occurs at line 1 of Algorithm 1) by:

$$\begin{aligned} X^{(3)} = \mathsf {HW}[M ] + N^{(3)} -\frac{n}{2} . \end{aligned}$$

(10)

Definition 4

We denote by ${\text {2O-CPA}}$ the $\mathsf {CPA}$ using the centered product as combination function. Namely:

$$\begin{aligned} \begin{array}{cccc} {\text {2O-CPA}}:&{} \mathbb {R}\times \mathbb {R}\times \mathbb {R}&{} \longrightarrow &{} \mathbb {F}_2^n \\ &{} \left( X^{(3)} , X^{\star } , Y \right) &{} \longmapsto &{} \displaystyle \mathop {{{\mathrm{argmax}}}}\limits _{k \in \mathbb {F}_2^n} \mathsf {\rho }\left[X^{(3)} \times X^{\star }, Y \right] . \end{array} \end{aligned}$$

A careful look at Definitions 2, 3 and Eq. (9) reveals that the only difference between the ${\text {MVA}}_{TR}$ and the ${\text {2O-CPA}}$ is the use of $X_{TR}$ instead of $X^{(3)}$. Thus, $X_{TR}$ will act as the leakage of the mask. Let us call $X_{TR}$ the second-order leakage.

Lemma 2

The informative part of the second-order leakage is the same as the informative part of the leakage mask, i.e.,

$$\begin{aligned} \mathbb {E}\left[X_{TR}|M = m \right]=\mathbb {E}\left[X^{(3)} |M = m \right]. \end{aligned}$$

Proof

It is a straightforward application of the results of [25]: Use Eq. (5) and notice the intentional $-2$ factor in Eq. (9). Both expectations are thus equal to $\mathsf {HW}[m ]$. $\square$

4.3 Leakage Analysis

By using the formula of the theoretical success rate (${\text {SR}}$), we show that as the same operations are targeted by the ${\text {MVA}}_{TR}$ and the ${\text {2O-CPA}}$. Consequently, it is equivalent to compare the ${\text {SNR}}$ or the ${\text {SR}}$ of these attacks. Based on this fact, we can theoretically establish the conditions in which the ${\text {MVA}}_{TR}$ outperforms the ${\text {2O-CPA}}$. These conditions are given in Theorem 3.

Recently, Ding et al. [11, §3.4] give the following formula to establish the Success Rate (${\text {SR}}$) of second-order attacks:

$$\begin{aligned} {\text {SR}}= \varPhi _{N_{k}-1}\left( \frac{\sqrt{b}\ \delta _0\delta _1}{4}K^{\frac{-1}{2}}\kappa \right) . \end{aligned}$$

(11)

In this formula:

• $\delta _0$ denotes the ${\text {SNR}}$ of the first share and $\delta _1$ denotes the ${\text {SNR}}$ of the second one;

• $\varPhi _{N_{k}-1}$ denotes the cumulative distribution function of $\left( N_{k}-1\right)$-dimensional standard Gaussian distribution; as underlined by the authors in [11], if the noise distribution is not multivariate Gaussian, then $\varPhi _{N_k}$ is to be understood as its cumulative distribution function;

• $N_k$ denotes the number of key candidates;

• K denotes the confusion matrix and $\kappa$ the confusion coefficient;

• b denotes the number of traces.

Remark 4

An updated version of this formula for first-order $\mathsf {CPA}$ has been presented in Eqn. (27) of [12] which solves the issue of the noninvertible matrix.

This formula allows to establish the link between the ${\text {SNR}}$ and ${\text {SR}}$ of second-order attacks against Boolean masking schemes.

Let us apply the Ding et al. formula in the case of our two attacks:

We target the same operation for the share that leaks the secret key ($X^{\star }$). Moreover by Remark 2, the informative parts of the leakages depending on the mask ($X_{TR}$ and $X^{(3)}$) is the same in the two leakages. As a consequence, K and $\kappa$ are the same in the two attacks.

It can be noticed that the only difference in the success rate formula is the use of instead of . Therefore, it is equivalent to compare these values and compare the ${\text {SR}}$ of these attacks.

Theorem 3

The ${\text {SNR}}$ of the “second-order leakage” is greater than the ${\text {SNR}}$ of the leakage of the mask if and only if

$$\begin{aligned} \sigma ^2 \leqslant 2 ^{n-2}-\frac{n}{2}, \end{aligned}$$

where $\sigma$ denotes the standard deviation of the Gaussian noise.

As a consequence, ${\text {MVA}}_{TR}$ will be better than ${\text {2O-CPA}}$ in the interval $\sigma ^2\in [0,2^{n-2}-n/2]$.

Proof

See “Appendix A.” Interestingly, the same result is also a byproduct of the demonstration of Proposition 8 (see “Appendix B.2”). $\square$

Theorem 3 gives us the cases where exploiting the second-order leakage will give better results than exploiting the classical leakage of the mask. For example, if $n=8$ (the case of AES) the second-order leakage is better until $\sigma ^2 \leqslant 60$.

Figure 2 shows when the ${\text {SNR}}$ of $X_{TR}$ is greater than the ${\text {SNR}}$ of $X^{(3)}$. In order to have a better representation of this interval, $\frac{1}{{\text {SNR}}}$ is plotted.

Fig. 2

Comparison between the variance of the noise for the classical leakage and the second-order and the impact of these noises on the SNR

4.4 Simulation Results

In order to validate empirically the results of Sect. 4, we test the method presented on simulated data. The target is a first-order protected AES with table recomputation. To simulate the leakages, we assume that each value leaks its Hamming weight with a Gaussian noise of standard deviation $\sigma$. The 512 leakages of the table recomputation are those given in Sect. 4.2.

A total of 1000 attacks are realized to compute the success rate of each experiment. In this part, the comparisons are done on the number of traces needed to reach 80% of success.

It can be seen in Fig. 3a and in Fig. 3b that the difference between the two attacks is null for $\sigma =0$ and $\sigma =8$ (that is, $\sigma ^2=64 \approx 60$). It confirms the bound of the interval shown in Fig. 2. This also confirms that comparing the ${\text {SNR}}$ is equivalent to comparing the ${\text {SR}}$.

It can be seen in Fig. 3 that in presence of noise the ${\text {MVA}}_{TR}$ outperforms the ${\text {2O-CPA}}$. The highest difference between the ${\text {MVA}}_{TR}$ and ${\text {2O-CPA}}$ is reached when $\sigma =3$. In this case, the ${\text {MVA}}_{TR}$ needs 2500 traces to mount the attack, while the ${\text {2O-CPA}}$ needs 7500 traces. This represents a relative gain¹ of ${\approx }200$%. As shown in Fig. 3d, the relative gain decreases to 122% when $\sigma =4$.

Fig. 3

Comparison between ${\text {2O-CPA}}$ and ${\text {MVA}}_{TR}$. a $\sigma =0$. b $\sigma =8$. c $\sigma =3$. d $\sigma =4$

4.5 Theoretical Analysis of the ${\text {SR}}$

While the previous analysis of Sect. 4.3 gives the bounds of effectiveness of the ${\text {MVA}}_{TR}$, it does not allow a quantitative comparison of the respective behaviors of the ${\text {MVA}}_{TR}$ and the ${\text {2O-CPA}}$ between these bounds. In this subsection, we propose an approach which allows a deeper analysis of the relevant parameters of their ${\text {SR}}$. We exploit the results of [15] which presents a closed form formula which links the ${\text {SR}}$ to the ${\text {SNR}}$ for first-order attacks. These results have recently been extended to high-order attacks [16].

Proposition 4

([15, Corollary 1]) The ${\text {SR}}$ of an additive distinguisher satisfies:

$$\begin{aligned} 1-{\text {SR}}\approx \exp {\left( -{\text {SE}}\times q\right) }, \end{aligned}$$

(12)

where ${\text {SE}}$ is the success exponent and q the number of traces used for the attack.

Proof

The proof is given in [15]. $\square$

Proposition 5

The ${\text {SE}}$ of the ${\text {2O-CPA}}$ is:

$$\begin{aligned} {\text {SE}}_{{\text {2O-CPA}}} = \min _{k \ne k^{\star }} \frac{ \kappa \left( k^{\star },k \right) }{ 2 \left( \frac{\kappa '\left( k^{\star },k \right) }{\kappa \left( k^{\star },k \right) } - \kappa \left( k^{\star },k \right) \right) +2 \left( \alpha _1 ^{-2} \sigma _1^2 + \alpha _2 ^{-2} \sigma _2^2 + \alpha _1 ^{-2} \sigma _1^2 \alpha _2 ^{-2} \sigma _2^2 \right) } , \end{aligned}$$

(13)

where in our case [which complies to Eq. (2) of Definition 1]:

$$\begin{aligned}&\alpha _1^2=\alpha _2^2 =\text {Var}\left[\mathbb {E}\left[X^{\left( 3\right) }|M \right] \right] = \text {Var}\left[\mathbb {E}\left[X^{\star }|M,T \right] \right] =\sqrt{\frac{n}{4}} , \\&\sigma _1^2 = \sigma _2^2 = \mathbb {E}\left[\text {Var}\left[X^{\left( 3\right) }|M \right] \right] = \mathbb {E}\left[\text {Var}\left[X^{\star }|M ,T \right] \right] = \sigma ^2 , \\&\kappa \left( k^{\star },k \right) \text { and } \kappa '\left( k^{\star },k \right) \text { are general confusion coefficients defined in} \\&\qquad \text {Definition~8 of }[15].~\text {Notice that }\kappa \left( k^{\star },k \right) \text { is a natural extension} \\&\qquad \text {of the seminal coefficient introduced by Fei et al. in }[13]. \end{aligned}$$

Proof

See “Appendix B.1.” $\square$

We note that $\alpha _i^2$ and $\sigma _i^2$ respectively represent the power of the signal and of the noise.

As Definitions 2, 3 and Eq. (9) reveal that the only difference between the ${\text {MVA}}_{TR}$ and the ${\text {2O-CPA}}$ is the use of $X_{TR}$ instead of $X^{(3)}$. Thus, we can directly compute the success exponent of ${\text {MVA}}_{TR}$.

Proposition 6

The ${\text {SE}}$ of the ${\text {MVA}}_{TR}$ is:

$$\begin{aligned} {\text {SE}}_{{\text {MVA}}_{TR}} = \min _{k \ne k^{\star }} \frac{ \kappa \left( k^{\star },k \right) }{ 2 \left( \frac{\kappa '\left( k^{\star },k \right) }{\kappa \left( k^{\star },k \right) } - \kappa \left( k^{\star },k \right) \right) +2 \left( \alpha _1 ^{-2} \sigma _1^2 + \alpha _2 ^{-2} \sigma _2^2 + \alpha _1 ^{-2} \sigma _1^2 \alpha _2 ^{-2} \sigma _2^2 \right) }, \end{aligned}$$

(14)

where in our case

$$\begin{aligned}&\alpha _1^2=\alpha _2^2 =\text {Var}\left[\mathbb {E}\left[ X_{TR}|M \right] \right] = \text {Var}\left[\mathbb {E}\left[X^{\star }|M,T \right] \right] =\sqrt{\frac{n}{4}} , \\&\sigma _1^2 = \mathbb {E}\left[\text {Var}\left[ X_{TR}|M \right] \right] = 4 \times \left( \frac{\sigma ^2}{2^n} \times \frac{n}{2} + \frac{\sigma ^4}{2^n} \right) , \\&\sigma _2^2 = \mathbb {E}\left[\text {Var}\left[X^{\star }|M ,T \right] \right] = \sigma ^2. \end{aligned}$$

Proof

The proof is similar as the proof of Proposition 5 using the values of noise computed in the “Appendix A.” $\square$

Exploiting this values, it is possible to extract the parameters which impact the respective behavior of the two attacks and especially the ones reaching to a higher difference between the two attacks. Similarly to Sect. 4.4, we will compare the two attacks using the relative gain.

Definition 5

(${\text {rel-gain}}^{\left( {\text {SR}}\right) }$) The relative gain between ${\text {2O-CPA}}$ and ${\text {MVA}}_{TR}$ is given by:

$$\begin{aligned} {\text {rel-gain}}^{\left( {\text {SR}}\right) }= \frac{m_{{\text {2O-CPA}}}^{\left( {\text {SR}}\right) }-m_{{\text {MVA}}_{TR}}^{\left( {\text {SR}}\right) }}{m_{{\text {MVA}}_{TR}}^{\left( {\text {SR}}\right) }}, \end{aligned}$$

where $m_{{\text {2O-CPA}}}^{\left( {\text {SR}}\right) }$ and $m_{{\text {MVA}}_{TR}}^{\left( {\text {SR}}\right) }$ are, respectively, the number of traces needed by ${\text {2O-CPA}}$ and ${\text {MVA}}_{TR}$ to reach success rate value ${\text {SR}}$.

And we will also use the difference in number of traces needed to reach ${\text {SR}}$.

Definition 6

(${\text {gain}}^{\left( {\text {SR}}\right) }$) The difference in number of traces needed to reach ${\text {SR}}$ of success is given by the gain:

$$\begin{aligned} {\text {gain}}^{\left( {\text {SR}}\right) }= m_{{\text {2O-CPA}}}^{\left( {\text {SR}}\right) }-m_{{\text {MVA}}_{TR}}^{\left( {\text {SR}}\right) }, \end{aligned}$$

where $m_{{\text {2O-CPA}}}^{\left( {\text {SR}}\right) }$ and $m_{{\text {MVA}}_{TR}}^{\left( {\text {SR}}\right) }$ are respectively the number of traces needed by ${\text {2O-CPA}}$ and ${\text {MVA}}_{TR}$ to reach ${\text {SR}}$ of success rate.

Notice that ${\text {rel-gain}}^{\left( {\text {SR}}\right) }$ and ${\text {gain}}^{\left( {\text {SR}}\right) }$ are tools to compare attacks after having computed their ${\text {SR}}$. They differ from relative distinguishing margins metrics [32] which analyses the value of the distinguisher (and not their ${\text {SR}}$).

Proposition 7

${\text {rel-gain}}^{\left( {\text {SR}}\right) }$ does not depend on the value of ${\text {SR}}$.

Proof

See “Appendix B.2.” $\square$

This means that, in Fig. 3, the ${\text {SR}}$ curves for ${\text {2O-CPA}}$ and ${\text {MVA}}_{TR}$ are the same, modulo a scaling in the X-axis. For instance, in Fig. 3a, b, the scaling factor is 1, i.e., the two curves superimpose perfectly. As a result, one can compare these two attacks in terms of traces number to extract the key, irrespective of the ${\text {SR}}$ value chosen for the threshold.

Proposition 8

${\text {gain}}^{\left( {\text {SR}}\right) }$ depends on the value of ${\text {SR}}$, but the value of the noise variance where ${\text {gain}}^{\left( {\text {SR}}\right) }$ is maximum not depends on ${\text {SR}}$.

Proof

See “Appendix B.3.” $\square$

Remark 5

While the bounds of Theorem 3 depend only on the ${\text {SNR}}$ the maximum effectiveness (the maximum of ${\text {gain}}^{\left( {\text {SR}}\right) }$ or ${\text {rel-gain}}^{\left( {\text {SR}}\right) }$) of the ${\text {MVA}}_{TR}$ compare to the ${\text {2O-CPA}}$ also depends on the operation targets (e.g., $\mathsf {AddRoundKey}$ or $\mathsf {SubBytes}$) by the confusion coefficients $\kappa$ and $\kappa '$.

Numerical results. In order to validate our theoretical analysis, we build empirical validation based on simulations. We reuse the curves generated for Sect. 4.4. In Fig. 4, the empirical results based simulation are plotted in gray and the Theoretical ones in red pointed lines. The first observation is that the theoretical analysis match well the simulations which validates our model choices.

In Fig. 4a, it can be noticed that for several ${\text {SR}}$ (different gray lines) the empirical ${\text {rel-gain}}^{\left( {\text {SR}}\right) }$ are closed which confirmed Proposition 7. Exploiting the formula of Definition 5, we can find the noise variance $\sigma ^2$ where ${\text {rel-gain}}^{\left( {\text {SR}}\right) }$ is maximum. Indeed, it occurs in a root of the derivative of ${\text {rel-gain}}^{\left( {\text {SR}}\right) }$. In our scenario, it occurs for $\sigma ^2 = 9.11$ (that is $\sigma \approx 3.02$). For this value of $\sigma ^2$, the relative gain is about equal to 2, that is, our ${\text {MVA}}_{TR}$ attacks requires three times less traces than the ${\text {2O-CPA}}$ to extract the key.

The behavior of ${\text {gain}}^{\left( {\text {SR}}\right) }$ is different indeed the ${\text {SR}}$ has an impact on it; the gray lines are not superimposed (see Fig. 4b). But similarly to ${\text {rel-gain}}^{\left( {\text {SR}}\right) }$, the ${\text {SR}}$ does not impact the value of noise where the maximum ${\text {gain}}^{\left( {\text {SR}}\right) }$ is reached. This confirms Proposition 8. In our scenario, it is reached for $\sigma ^2 = 39.67$ (that is $\sigma \approx 6.30$).

In order to compute this maximum, we have computed the roots of the derivatives (of ${\text {rel-gain}}^{\left( {\text {SR}}\right) }$ and ${\text {gain}}^{\left( {\text {SR}}\right) }$ w.r.t. $\sigma ^2$) using the MAXIMA software.

Fig. 4

Comparison between the ${\text {2O-CPA}}$ and the ${\text {MVA}}_{TR}$. a rel-gain$^{\hbox {(SR)}}$. b gain$^{\hbox {(SR)}}$

5 An Example on a High-Order Countermeasure

The result of the previous section can be extended to any masking scheme based on table recomputation. In particular, the ${\text {MVA}}_{TR}$ can apply to high-order masking schemes.

5.1 Coron Masking Scheme Attack and Countermeasure

The table recomputation countermeasure can be made secure against high-order attacks. An approach has been proposed by Schramm and Paar [28]. However, it happened that this masking scheme can be defeated by a third-order attack [8]. To avoid this vulnerability, Coron recently presented [7] a new method based on table recomputation, which guarantees a truly high-order masking. The core idea of this method is to mask each output of the S-Box with a different mask and refresh the set of masks between each shift of the table (masking the inputs by one mask). HV attacks are still a threat against such schemes. Indeed, an attacker will recover iteratively each input mask. Afterward, he will be able to perform a first-order attack on the AddRoundKey to recover the key. To prevent attacks based on the exploitation of the leakages of the input masks an approach based on a random shuffling of the loop index is possible (see Algorithm 2). Algorithm 2 is a $(d-1)$-th-order countermeasure, meaning that attacks of order strictly less than d fail. In this algorithm, the $x_i$ for $i<d$ can be seen indifferently as shares or as masks. The original masked S-Box algorithm from Coron [7] is the same as Algorithm 2, with $\varphi$ chosen as the identity. It can be noticed that the entropy needed to build the permutation could be low compared to the entropy needed for the masking scheme (especially because of the numerous costly $\mathsf {RefreshMasks}$ operations).

5.2 Attack on the Countermeasure

We apply Algorithm 2 on X which is equal to $T\oplus k^\star$, i.e., $\bigoplus _{i=1}^d X_i = T\oplus k^\star$. Similarly to the definitions in Sect. 4.2, let us define the leakages of the table recomputation of the masking scheme of Coron where the order of the masking is $d-1$: $X_{ \left( \omega ,i,j \right) }^{(1)} = \mathsf {HW}[ \varPhi \left( \omega \right) \oplus X_{i} ] + N_{\left( \omega , i,j \right) }^{(1)} -\frac{n}{2}$ and $X_{\left( \omega ,i,j \right) }^{(2)} = \mathsf {HW}[\varPhi \left( \omega \right) ] + N_{\left( \omega ,i,j \right) }^{(2)} -\frac{n}{2}$, where $i \in \llbracket 1,d-1 \rrbracket$ will index the $d-1$ masks. The d-th share is the masked sensitive value. Besides $j\in \llbracket 1,d \rrbracket$ denotes the index of the loop from lines 7 to lines 9 of the Algorithm 2. The leakage of the masks is given by $X^{(3)}_{i} = \mathsf {HW}[X_{i} ] + N^{(3)}_{i} -\frac{n}{2}$. Finally, we denote by: $X^{\star } = \mathsf {HW}[ \bigoplus _{i=1}^{d-1} X_i \oplus k^{\star } \oplus T ] + N -\frac{n}{2}$ the leakage of the masked value.

Definition 7

The combination function ${\text {C}}_{CS}^{d}$ exploiting the leakage of the table recomputation (Coron Scheme, abridged CS) is given by:

$$\begin{aligned} \begin{array}{cccc} {\text {C}}_{CS}^{d}:&{} \mathbb {R}^{ d\times \left( d-1 \right) \times 2^{n+1}}\times \mathbb {R}&{} \rightarrow &{} \mathbb {R}\\ &{} \! \left( \! \left( \! X_{\left( \! \omega ,i,j \! \right) }^{(1)}, X_{\left( \! \omega ,i,j \! \right) }^{(2)} \right) \! _{\begin{array}{c} \omega \in \mathbb {F}_{2^n} \\ i \in \llbracket 1,d \! - \! 1 \rrbracket \\ j \in \llbracket 1,d \rrbracket \end{array}} , X^{\star } \! \right) \! &{} \! \mapsto \! &{} \!\displaystyle \prod _{i=1}^{d-1} \! \left( \!\frac{-2}{d 2^n} \! \sum _{\begin{array}{c} \omega \in \mathbb {F}_{2^n} \\ j \in \llbracket 1,d \rrbracket \end{array}} \! X_{\left( \! \omega ,i,j \! \right) }^{(1)} \! \times \! X_{\left( \! \omega ,i,j \! \right) }^{(2)} \right) \! \times \! X^{\star } . \end{array} \end{aligned}$$

Similarly to Sect. 4.3, we define for all $1\leqslant i\leqslant d-1$:

$$\begin{aligned} X_{CS_i^{d}} = \displaystyle {\frac{-2}{d 2^n} \sum _{\begin{array}{c} \omega \in \mathbb {F}_{2^n} \\ j \in \llbracket 1,d \rrbracket \end{array}} X_{\left( \omega ,i,j \right) }^{(1)} \times X_{\left( \omega ,i,j \right) }^{(2)}} . \end{aligned}$$

This value is the combination of all the leaking values of the table recomputation depending of one share.

Remark 6

The scaling by factor $-2/d$ allows to have, for all $i \in \llbracket 1, d-1 \rrbracket$:

$$\begin{aligned} \mathbb {E}\left[X_{CS_i^{d}}|X_i = x_i \right]=\mathbb {E}\left[X^{(3)}_i |X_i = x_i \right]. \end{aligned}$$

Additionally, we define for, $i = d$, $X_{CS_i^{d}} = X^{\star }$. Based on the combination function ${\text {C}}_{CS}^{d}$, a multivariate attack can be built.

Definition 8

The multivariate attack exploiting the leakage of the table recomputation of the $d-1$-order Coron masking Scheme is given by:

where $Y= (-1)^{d-1} \times \left( \mathsf {HW}[T \oplus k ] - \frac{n}{2} \right)$.

Proposition 9

${\text {MVA}}_{CS}^d$ is sound.

Proof

The demonstration follows the same lines as that of Proposition 1. In the case of Proposition 9, the expectation of $\prod _{i=1}^{d}\left( X_{CS_i^{d}} \right)$ knowing the plaintext $T=t$ is proportional to $\mathsf {HW}[t \oplus k ]$. Indeed by [27] $\mathbb {E}\left[\prod _{i=1}^{d}\left( X_{CS_i^{d}} \right) | T =t \right] = \left( \frac{-1}{2} \right) ^{d-1} \times \left( \mathsf {HW}[t \oplus k ] - \frac{n}{2} \right)$ $\square$

Remark 7

The attack presented in Definition 8 is a $(d \times \left( d-1 \right) \times 2^{n+1}+1)$-variate $(2\times \left( d-1 \right) +1)$-order attack.

Definition 9

The “classical” ${\text {dO-CPA}}$ is the HOCPA build by combining the d shares using the centered product combination function.

$$\begin{aligned} \begin{array}{cccc} {\text {dO-CPA}}:&{} \mathbb {R}^{d-1} \times \mathbb {R}\times \mathbb {R}&{} \longrightarrow &{} \mathbb {F}_2^n \\ &{} \left( \left( X_i^{(3)} \right) _{ i \in \llbracket 1,d-1 \rrbracket } , X^{\star } , Y \right) &{} \longmapsto &{} \displaystyle {{\mathrm{argmax}}}_{k \in \mathbb {F}_2^n} \mathsf {\rho }\left[\prod _{i=1}^{d-1} X_i^{(3)} \times X^{\star }, Y \right] . \end{array} \end{aligned}$$

5.3 Leakage Analysis

The difference between the two attacks is the use of $X_{CS_i^{d}}$ instead of $X_i^{(3)}$ as the leakage of the $d-1$ shares which do not leak the secret key. Ding et al. [11, §3.4] also provides a formula to compute the ${\text {SR}}$ of HOCPA.

Similarly to Sect. 4, the only differences in the formula are the ${\text {SNR}}$ of the shares which do not leak the key. Then by comparing the and , we compare the success rate of the attacks. It can be noticed that in our model the ${\text {SNR}}$ does not depend on i.

Theorem 10

The ${\text {SNR}}$ of the “second-order leakage” is greater than the ${\text {SNR}}$ of the leakage of the mask if and only if

$$\begin{aligned} \sigma ^2 \leqslant d \times 2^{n-2} - \frac{ n }{ 2}, \end{aligned}$$

(15)

where $\sigma$ denotes the standard deviation of the Gaussian noise.

As a consequence, ${\text {MVA}}_{CS}^d$ will be better than ${\text {dO-CPA}}$ when the noise variance lays in the interval $[0,d\times 2^{n-2} - n/2]$. We can immediately deduce that the size of the useful interval of variance increases linearly with the order of the masking scheme.

Proof

See “Appendix C.” $\square$

Figure 5 shows the impact of the attack order d on the interval of noise where the ${\text {MVA}}_{CS}^d$ outperforms ${\text {dO-CPA}}$ (let us call this interval the useful interval of variance denoted by UIoV). We can see that the size of these intervals increases with the order. For example, for $d=3$ the useful interval of variance is $\left[ 0, 188 \right]$. In practice, it is very difficult to perform a third-order attack with a noise variance of 188. Indeed, recall that the number of traces to succeed an attack with probability 80% is proportional to the inverse of the SNR [15].

Fig. 5

Comparison between the signal-to-noise ratio of $X^{(3)}_i$ and signal-to-noise ratio of $X_{CS_i^{d}}$ (where d is the attack order)

5.4 Simulation Results on Coron Masking Scheme

In order to validate the theoretical results of Sect. 5.3, the ${\text {MVA}}_{CS}^d$ has been tested on simulated data and compared to ${\text {dO-CPA}}$. The simulations have been done with the Hamming weight model and Gaussian noise such as the leakages defined in Sect. 5.2. We test these attacks against a second- and a third-order masking schemes.

To compute the success rate, attacks are redone 500 times for the second-order masking and 100 times for the third-order masking (because this attack requires an intensive computational power).

In Fig. 6a, it can be seen that MVA$^{(3)}_{CS}$ reaches 80% of success rate for less than 20,000 traces while the 3O-CPA does not reach 30% for 100,000. In Fig. 6b, it can be seen that MVA$^{(4)}_{CS}$ reaches 80% of success rate for less than 200,000 traces while the 4O-CPA does not reach 5%.

Fig. 6

Comparison between dO-CPA and MVA$^{d}_{CS}$. a $d=3, \sigma =3$. b $d=4, \sigma =3$

6 A Note on Affine Model

In Sects. 4 and 5, the leakage function was expected to be the Hamming weight. Let us now study the impact of the leakage function on the ${\text {MVA}}_{TR}$ attack. We suppose that the leakage function is affine.

6.1 Properties of the Affine Model

Definition 10

(Affine leakage function) Let V the leaking value, $\alpha$ the weight of the leakage of each bit, and $\cdot$ the inner product in $\mathbb {R}^n$, that is $\alpha \cdot V = \sum _{i=1}^n \alpha _i V_i$. A leakage function $\varPsi _{\alpha }$ is said affine if this function is a weighted sum of the bits of the leaking value, i.e., $\varPsi _{\alpha }\left( V \right) = \alpha \cdot V$.

In the sequel, we assume sensitive variables are balanced and have each bit independent of the other, as is customary in cryptographic applications.

Proposition 11

Let $\mathbf {1}=(1,\ldots ,1)\in \mathbb {F}_2^n$.

$$\begin{aligned} \mathbb {E}\left[\varPsi _{\alpha }\left( V \right) \right]= \frac{1}{2}\left( \alpha \cdot \mathbf {1} \right) \quad \text {and}\quad \text {Var}\left[\varPsi _{\alpha }\left( V \right) \right]= \frac{1}{4} ||{\alpha }||_{2}^2. \end{aligned}$$

Proof

We have $\mathbb {E}\left[\varPsi _{\alpha }\left( V \right) \right] = \alpha \cdot \mathbb {E}\left[V \right] = \alpha \cdot \left( \frac{1}{2}\mathbf {1} \right)$ and $\text {Var}\left[\varPsi _{\alpha }\left( V \right) \right] = {\alpha }^\mathsf {t} \mathsf {Cov}\left[V \right] \alpha = \frac{1}{4} ||{\alpha }||_{2}^2$. $\square$

Then, it is possible to compute the results of the centered product.

Lemma 12

Let U be a random variable following a uniform law over $\mathbb {F}_2^n$, and $z \in \mathbb {F}_2^n$. We have:

$$\begin{aligned} \mathbb {E}\left[\left( \varPsi _{\alpha }\left( U \right) -\mathbb {E}\left[\varPsi _{\alpha }\left( U \right) \right] \right) \times \left( \varPsi _{\beta } \left( U \oplus z \right) -\mathbb {E}\left[\varPsi _{\beta } \left( U \oplus z \right) \right] \right) \right]= -\frac{1}{2} \left( \alpha \odot \beta \right) \cdot z + \frac{1}{4} \alpha \cdot \beta , \end{aligned}$$

where $\odot$ denotes the element-wise multiplication, that is $(\alpha \odot \beta )_i = \alpha _i \beta _i$.

Proof

See in “Appendix D.1.” $\square$

Assumption 1

In order to compare the results in case of an affine model and the Hamming weight model ($\mathsf {HW}=\varPsi _\mathbf {1}$), let us assume that the model variance is the same in the two cases, i.e., $\text {Var}\left[\varPsi _{\alpha }\left( V \right) \right]=\text {Var}\left[\mathsf {HW}[V ] \right]$; this is equivalent to $||{\alpha }||_{2}^2= n$.

Let us also assume that all the values manipulated during the algorithm leak in the same way, i.e., the weight vector $\alpha$ of the sum is the same for all the variables V of the algorithm. This is realistic because it is likely that sensitive variables transit through a given resource, e.g., the accumulator register.

In the rest of this section, we will denote by $\alpha$ the vector of weight of the leakage model.

Let us redefine the leakage of the table recomputation the (centered) leakage of the random index: $X_{\omega }^{(1)} = \alpha \cdot \left( \varPhi \left( \omega \right) \oplus M \right) + N_{\omega }^{(1)} - \frac{1}{2}\left( \alpha \cdot \mathbf {1} \right)$, the (centered) leakage of the mask random index: $X_{\omega }^{(2)} = \alpha \cdot \left( \varPhi \left( \omega \right) \right) + N_{\omega }^{(2)} - \frac{1}{2}\left( \alpha \cdot \mathbf {1} \right)$, the (centered) leakage of the mask: $X^{(3)} = \alpha \cdot M - \frac{1}{2}\left( \alpha \cdot \mathbf {1} \right)$, Besides, let $X^{\star }$ be the leakage of a sensitive value depending on the key. We have either:

• $X^{\star } = \alpha \cdot (T\oplus k^\star \oplus M) + N - \frac{1}{2}\left( \alpha \cdot \mathbf {1} \right)$, which is similar to Eq. (8), or

• $X^{\star } = \alpha \cdot (S(T\oplus k^\star )\oplus M) + N - \frac{1}{2}\left( \alpha \cdot \mathbf {1} \right)$, if there is an S-Box S.

In a view to unite both expressions, we denote by Z the sensitive variable, that is either $Z=T\oplus k^\star$, or $Z=S(T\oplus k^\star )$. Consequently, we have $X^{\star } = \alpha \cdot (Z\oplus M) + N - \frac{1}{2}\left( \alpha \cdot \mathbf {1} \right)$.

Lemma 13

In case of affine leakage model the second-order leakage $X_{TR}$ is given by:

$$\begin{aligned} \mathbb {E}\left[X_{TR}|M=m \right] = \mathbb {E}\left[\frac{-2}{2^n} \sum _{\omega = 0}^{2^n-1} X_{\omega }^{(1)} \times X_{\omega }^{(2)} \mid M=m \right] = \left( \alpha ^2 \right) \cdot m - \frac{1}{2} ||{\alpha }||_{2}^2, \end{aligned}$$

where $\alpha ^2 = \alpha \odot \alpha$.

Proof

Direct application of Lemma 12. $\square$

Proposition 14

In case of affine model, the leakages of the ${\text {MVA}}_{TR}$ (recall Definition 2) and the 2O-CPA are different. Indeed, let us denote $\alpha ^n =\underbrace{\alpha \odot \alpha \odot \cdots \odot \alpha }_{n \text { times}}$. We have:

$$\begin{aligned} \mathbb {E}\left[{\text {C}}_{TR}\left( \left( X_{\omega }^{(1)}, X_{\omega }^{(2)} \right) _{\omega } , X^{\star } \right) \mid T \right] =-\frac{1}{2} \alpha ^3 \cdot z + \frac{1}{4} \sum _{i=1}^n \alpha _i^3, \end{aligned}$$

and

$$\begin{aligned} \mathbb {E}\left[X^{(3)} \times X^{\star } \mid T \right]= -\frac{1}{2} \alpha ^2 \cdot z+ \frac{1}{4} ||{\alpha }||_{2}^2. \end{aligned}$$

Proof

Direct application of Lemmas 13 and 12. $\square$

6.2 Impact of the Model on the Confusion Coefficient

As the models in the two different attacks are different, the parameters K and $\kappa$ (recall Eq. (11)) also differ. In order to compare the two attacks, we first establish the impact of the model on the value of the minimum confusion coefficient $\min _{k\ne 0} \kappa _{k}$. Then, we show that the impact is not important in case of the targeted sensitive value is proceed in a nonlinear part of the algorithm (an S-Box).

In practice, the confusion coefficients are very close. We study the impact of the disparity of $\alpha$ using several distributions (see Fig. 7):

• $\alpha _i = \sqrt{1+\varepsilon }$ for i even and $\alpha _i = \sqrt{1-\varepsilon }$ otherwise (abridged $\alpha = \sqrt{1\pm \varepsilon }$),

• and the other sign convention (abridged $\alpha = \sqrt{1\mp \varepsilon }$).

We also randomly generate 1000 $\alpha$. All those distributions satisfy Assumption 1, namely $\sum _{i=1}^n \alpha _i^2 = n$.

The confusion coefficients for $\alpha ^2$ and $\alpha ^3$ are very close (see Fig. 7).

Moreover, we find that the maximum difference in all the simulations with random weight is $\max \left( \min _{k \ne 0} {_{\alpha ^2} \kappa _k} -\min _{k \ne 0} {_{\alpha ^3} \kappa _k} \right) =0.019$. In terms of number of traces needed to reach 80% of success, this represents a small difference of 5%.

Fig. 7

Comparison of $\min _{k\ne 0} \kappa _k$ for the ${\text {MVA}}_{TR}$ and the ${\text {2O-CPA}}$

6.3 Theoretical Analysis

Similarly to the Sect. 4.3, let us study the impact of the affine model on the success of the ${\text {MVA}}_{TR}$ compared to the ${\text {2O-CPA}}$.

As motivated in Sect. 4.1, we can modify the ${\text {MVA}}_{TR}$ in order to target the last round S-Box input: $X^{\star }= \alpha \cdot \left( \texttt {Sbox}^{-1}[T \oplus k^{\star } ] \oplus M \right) +N - \frac{1}{2}\left( \alpha \cdot \mathbf {1} \right)$.

Theorem 15

The ${\text {SNR}}$ of the “second-order leakage” is greater than the ${\text {SNR}}$ of the leakage of the mask if and only if

$$\begin{aligned} \sigma ^2 \leqslant ||{\alpha }||_{4}^4 \times \frac{2^{n-2}}{n} - \frac{n}{2}, \end{aligned}$$

where $||{\alpha }||_{p} = (\sum _{i=1}^n {|\alpha _i|}^p)^{1/p}$ is the p-norm $(p\geqslant 1$) of vector $\alpha$, and where $\sigma$ denotes the standard deviation of the Gaussian noise.

As a consequence, ${\text {MVA}}_{TR}$ is better than ${\text {2O-CPA}}$ when the noise variance is in the interval $[0,||{\alpha }||_{4}^4\, 2^{n-2}/n - n/2]$.

Proof

See “Appendix D.2.” $\square$

Corollary 16

The minimal value of $||{\alpha }||_{4}^4$ subject to $||{\alpha }||_{2}^2 = n$ is reached when all the component of $\alpha$ are equal. This means that the worst case for the ${\text {MVA}}_{TR}$ compared to the ${\text {2O-CPA}}$ is when the leakage is in Hamming Weight.

Proof

See “Appendix D.3.” $\square$

6.4 Simulation Results

Some simulations have been done in order to validate the results of the theoretical study of the previous sections. The results, presented in this section, confirm that:

• attacks are not impacted by the small differences of the confusion coefficient ($\kappa$, recall Sec. 6.2).

• attacks depend on the ${\text {SNR}}$ as predicted by Theorem 15.

For the purpose of the simulations, the target considered is the input of the S-Box of the last round; as a consequence, we consider

$$\begin{aligned} X^{\star }= \alpha \cdot \left( \texttt {Sbox}^{-1}[T \oplus k^{\star } ] \oplus M \right) +N - \frac{1}{2}\left( \alpha \cdot \mathbf {1} \right) . \end{aligned}$$

The mask M and the plain text T are randomly drawn from $\mathbb {F}_2^8$. The noises are drawn from a Gaussian distribution with different variances $\sigma ^2$. The results of the attacks are expressed using the success rate. To compute the success rates, the experiments have been redone 1000 times. For each experiment, the secret key $k^{\star }$ are randomly drawn over $\mathbb {F}_2^8$. To compare the efficiency of the two attacks, we compare the number of traces needed to reach 80% of success.

For the first experiment, we choose $\alpha =\sqrt{1\pm \varepsilon }$ (i.e., $\forall i$, $\textstyle \alpha _i = \sqrt{1 + ( -1 )^{i } \varepsilon }$).

Case $\varepsilon = 0.9$ In this case $||{\alpha }||_{4}^4=14.480$ and according to Theorem 15, the ${\text {MVA}}_{TR}$ should outperform the classical success rate in the interval $\left[ 0 , 111\right]$. It can be seen in Fig. 8a, b that in such case when $\sigma ^2 = 0$ or when $\sigma ^2 = 111$ the ${\text {MVA}}_{TR}$ and the ${\text {2O-CPA}}$ need the same number of traces to reach 80% of success. First of all, this confirms the soundness of our model. Second, it validates that, in case of affine model when the target is proceeded in a nonlinear part of the cryptographic algorithm, the main factor which makes attacks different is the ${\text {SNR}}$. When $\sigma =3$ the ${\text {2O-CPA}}$ needs around 3800 traces to reach 80% of success whereas the ${\text {MVA}}_{TR}$ needs around 1000 traces (see Fig. 8c). This represents a relative gain of 280%. Compared to the relative gain observed in case of the Hamming weight model (recall Fig. 3c), this confirms that the ${\text {MVA}}_{TR}$ performs better compare to the ${\text {2O-CPA}}$ in case of an affine model. It can be seen in Fig. 8d, when the $\sigma =4$, the number of traces needed to reach 80% of success is around 2500 for the ${\text {MVA}}_{TR}$ and around 10,000 for the ${\text {2O-CPA}}$; this represents a relative gain of 300%.

Fig. 8

Comparison between ${\text {2O-CPA}}$ and ${\text {MVA}}_{TR}$ for $\varepsilon = 0.9$. a $\sigma =0$. b $\sigma =10.54$. c $\sigma =3$. d $\sigma =4$

Case $\varepsilon = 0.5$ When $\varepsilon = 0.5$, $||{\alpha }||_{4}^4=10$; consequently, Theorem 15 predicts that the ${\text {MVA}}_{TR}$ should outperform ${\text {2O-CPA}}$ in the interval $\left[ 0, 76\right]$. It can be seen in Fig. 9a, b that in such case when $\sigma ^2 = 0$ or when $\sigma ^2 = 76$ the ${\text {MVA}}_{TR}$ and the ${\text {2O-CPA}}$ need the same number of traces to reach 80% of is success. This confirms the results of Theorem 15.

It can be seen in Fig. 9c that when $\sigma = 3$ the ${\text {MVA}}_{TR}$ needs around 1000 traces to reach 80% of success whereas the ${\text {2O-CPA}}$ needs 3500 traces. The relative gain of use the ${\text {MVA}}_{TR}$ is 250%. When $\sigma = 4$ then the number of traces needed by the ${\text {MVA}}_{TR}$ to reach 80% of success is around 3000. The number of traces needed by the ${\text {2O-CPA}}$ is around 9000. The relative gain of the ${\text {MVA}}_{TR}$ with respect to the ${\text {2O-CPA}}$ is 200%.

Fig. 9

Comparison between ${\text {2O-CPA}}$ and ${\text {MVA}}_{TR}$ for $\varepsilon = 0.5$. a $\sigma =0$. b $\sigma =8.71$. c $\sigma =3$. d $\sigma =4$

For one bit attacks The best case for ${\text {MVA}}_{TR}$ compared to the ${\text {2O-CPA}}$ is when all the bits are zero except one (see “Appendix D.3”). Let us compare the two attacks in a such case. We assume that all the coordinates of $\alpha$ are equal to zero except the most significant bit. As $||{\alpha }||_{4}^4=64$, the useful interval of variance is $\left[ 0 , 508 \right]$. It can be seen in Fig. 10a that when the noise is null both attacks perform in the same way. It confirms that also in this case the difference resides in the ${\text {SNR}}$. When $\sigma = 8$ the ${\text {MVA}}_{TR}$ reach 80% of success with 25,000 traces, whereas the ${\text {2O-CPA}}$ needs 175,000; this represents a relative gain of 600% (see Fig. 10b).

Fig. 10

Comparison between the ${\text {2O-CPA}}$ and the ${\text {MVA}}_{TR}$ in case of one bit model in presence of high Gaussian noise. a $\sigma =0$. b $\sigma =8$

7 Practical Validation

This section presents the results of the multivariate attack exploiting the table recomputation stage on true traces.

7.1 Experimental Setup

The traces are electromagnetic leakages of the execution of an AES-128 assembly implementation with table recomputation. Our implementation has been loaded on ATMEL ATMega163 8-bit to be analyzed. This smartcard is known to be leaky. It contains 16 Kb of in-system programmable flash, 512 bytes of EEPROM, 1 Kb of internal SRAM and 32 general purpose working registers. The smartcard is controlled by a computer through the Xilinx Spartan-VI FPGA embedded in a SASEBO-W platform. The ATMega is powered at 2.5 V and clocked at 3.57 MHz.

The measurements were taken using a LeCroy wave-runner 6100A oscilloscope by means of a Langer EMV 0–3 GHz EM probe and PA-303 30 dB Langer amplifier. The acquisitions have been acquired with full bandwidth and with a sampling rate of $F_S=500$ MS/s.

To build our experiments, 13,000 traces have been acquired. Each trace contains 12 million leakages samples in order to simplify our analysis we only acquired the table recomputation step and the first round of the AES.

7.2 Experimental Results

Let us first study the results of the attack in terms of success rate. The leakage function has been recovered using a linear regression. For example, the normalized vector of weight for the leakage of the first share is

$$\begin{aligned} \alpha = \left( 0.95, 1.22, 0.98, 1.13, 0.59, 1.01, 1.04, 0.95 \right) . \end{aligned}$$

Both the ${\text {MVA}}_{TR}$ and the ${\text {2O-CPA}}$ target $\texttt {Sbox}[T \oplus k^{\star } ] \oplus M$ as in our implementation the input and output masks are the same.

It can be seen in Fig. 11a that the results of the two attacks are similar. Both attacks perform similarly because the curves are not noisy.

Indeed, the average values of the ${\text {SNR}}$ of the 256 leakages of the masked random index ($\varPhi \left( \omega \right) \oplus M$) and the ${\text {SNR}}$ of the 256 leakages of the random index ($\varPhi \left( \omega \right)$) is 5.

Fig. 11

Comparison of the ${\text {SR}}$ of the ${\text {MVA}}_{TR}$ and the ${\text {2O-CPA}}$. a Comparison on raw traces. b Comparison with noise addition

If we assume that the variance of the signal is equal to two (such as HW on 8-bit CPUs), then the variance of the noise is less than 0.5. The mask (M) and the key-dependent share ($\texttt {Sbox}[T \oplus k^{\star } ] \oplus M$) leak with a ${\text {SNR}}$ of 14 which corresponds to a noise variance of 0.1, which is very low (compared to the upper bound of the useful interval of variance given in Theorem 3, namely 60).

This two results are specific to the implementation and a clear disadvantage for the ${\text {MVA}}_{TR}$. But even in this case the ${\text {MVA}}_{TR}$ works as well as the ${\text {2O-CPA}}$, this shows that there is (generally) a gain to use the ${\text {MVA}}_{TR}$.

In order to confirm these results, let us verify that when the noise increases the ${\text {MVA}}_{TR}$ outperforms the ${\text {2O-CPA}}$. Let us add an artificial Gaussian noise with a standard deviation of 0.0040. This models the addition of a countermeasure on top of the table recomputation. Then, it can be seen in Fig. 11b that in this case the ${\text {MVA}}_{TR}$ outperforms the ${\text {2O-CPA}}$. This confirms the practicality of our attack and also that the gain is in the ${\text {SNR}}$.

8 Countermeasure

The ${\text {MVA}}_{TR}$ represents a threat against block ciphers with table recomputation step. In order to mitigate this new vulnerability, we present in this section a countermeasure, depicted in Algorithm 3. This countermeasure will ensure the security against the new proposed attack. We present it in the context of a first-order masking scheme, but this countermeasure is generic and as a consequence can be applied in a higher-order masking scheme such as the masking scheme of Coron.

Remark 8

The proposed countermeasure tackles the input masks vulnerability. The protection of the output mask is easier as all the output masks can be different for all the table entries.

8.1 Countermeasure Principle

The core idea of this countermeasure is to randomly draw permutations not all over the possible permutations but only over a particular kind of permutations: the ones which are commutative with S (the $\textsf {SubBytes}$ function).

Definition 11

A permutation $f : \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ is said to be commutative with respect to the function $g: \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ and the composition law if and only if $f\left( g \left( x\right) \right) = g\left( f\left( x\right) \right) , \forall x \in \mathbb {F}_2^n$.

Exploiting this kind of function, the countermeasure principle is as follow: As random permutation, a commutative permutation with respect to S is drawn. Let us call the permutation $\gamma$. Exploiting the commutative property of the random permutation, $\gamma ( S[\omega ])$ is computed instead of $S[ \gamma \left( \omega \right) ]$ (line 5 of Algorithm 3). Contrast this line with line 5 of Algorithm 1. As a consequence, if an attacker combines the leakages of the random mask index (line 4) and the random index (line 5) the obtained value depends very little in the masks m and $m^{\prime }$ (see in-depth analysis in Sect. 8.3).

8.2 Implementations

The major issue of the countermeasure in an implementation perspective is to randomly generate a commutative permutation.

A first approach could be to generate off-line a large enough set of permutations and store them into the device. At each execution using a random number, a permutation will be selected. Of course such approach can be prohibitive in terms of memory need and as a consequence is not applicable.

A probably better approach is to generate on-the-fly a commutative permutation. In this subsection, we give an example of a such algorithm. The idea is to randomly generate a power (with respect to the combination law) of the $\textsf {SubBytes}:S$ bijection.

Definition 12

The power $p \in \mathbb {N}$ of the function S is given by:

$$\begin{aligned} \begin{array}{cccc} S^{p} :&{} \mathbb {F}_2^{n} &{} \longrightarrow &{} \mathbb {F}_2^n \\ &{} x &{} \longmapsto &{} \displaystyle \underbrace{S \circ S \circ \ldots \circ S}_p\left( x \right) , \end{array} \end{aligned}$$

where $\circ$ denotes the composition law.

Proposition 17

The bijections $S^p: \mathbb {F}_2^{n} \longrightarrow \mathbb {F}_2^n$ and $S: \mathbb {F}_2^{n} \longrightarrow \mathbb {F}_2^n$ are commutative $\forall p \in \mathbb {N}$.

In order to generate a random power of S, it is possible to directly compute $S^r$ by applying r times the permutation S where r is a random number. Notice that r can be larger than the number of possible power S by the group law property of the combination. But this approach can be time consuming.

In a view to accelerate this operation, the use of the cycle decomposition of S may be an interesting approach. Let us recall this well known theorem:

Proposition 18

(Theorem 5.19 [9]) Let $S_n$ be the symmetric group of n elements, then each element of $S_n$ can be expressed as a product of disjoint cycles.

Proposition 19

The maximum number of exponentiations needed to compute $S^p$ could be reduced from p to $p \pmod {l_1} + p \pmod {l_2} + \ldots +p \pmod {l_m}$ where the $l_i$ denote the respective length of the cycles in the cycles decomposition of S. Notice that $l_1 + l_2 + \cdots + l_m = 2^n$.

Proof

We can express S as $S = c_1 \circ c_2 \circ \cdots \circ c_m$ by Proposition 18. As the order of a cycle is equal to its length l, we have that:

$$\begin{aligned} S^p =c_1^{p \pmod {l_1}} \circ c_2^{p \pmod {l_2}} \cdots \circ c_m^{p \pmod {l_m}}. \end{aligned}$$

$\square$

Example 20

Let us take as example of S the $\textsf {SubBytes}$ function of AES. This permutation can be decomposed on five disjoint cycles of respectively length $l_1 = 59, \, l_2 = 81, \, l_3 = 87,\, l_4 = 27, \, l_5 = 2$. The order of S in this case is $\mathrm {lcm}\left( 59,81,87,27,2\right) = 277{,}182$. As a consequence, the computation of $S^{277{,}182}$ requires a maximum of 256 table evaluations.

8.3 Security Analysis

The security provided by this countermeasure results from different working factors. Of course the first one is to ensure that the ${\text {MVA}}_{TR}$ is still unfeasible or at least less effective than the ${\text {2O-CPA}}$ which would remain feasible. We validated this security using simulation with the same setup as in Sect. 4.4. Namely we assume that each value leaks its Hamming weight with a Gaussian noise of standard deviation $\sigma$. A total of 1000 attacks has been realized to compute the success rate of each experiment.

The attacker can combine multiplicatively $\gamma \left( S[\omega ] \right)$ with $\gamma \left( \omega \right)$. The results of the attack resulting from this combination can be found in Fig. 12 for two different noise standard deviations. We can immediately see that in this case the ${\text {MVA}}_{TR}$ does not allow to recover the key.

Fig. 12

${\text {MVA}}_{TR}$ with commutative bijection as countermeasure (Algorithm 3). a $\sigma =2$. b $\sigma =3$

The second working factor for the countermeasure of Algorithm 3 is the number of possible commutative permutations. Indeed, if this number is too low an attacker can test all the permutations and build attacks such as in [30]. For example using the possible powers of S in AES, we reach a total count of 277,182 bijections commutating with S, which is hard to exhaustively test but remains possible.

Of course another aspect of the countermeasure is the security of the permutation generation itself against possible side-channel analysis. If an attacker is able for example to recover: $p \pmod {l_1}, \, p \pmod {l_2} , \, \ldots , \, p \pmod {l_m}$, he will be able to recover the random permutation. This means that at least the exponentiation of S should be executed in constant time.

8.4 Implementation Analysis

The countermeasure presented previously may have an impact both on the time and on the entropy needed for the table recomputation step. Interestingly the entropy, i.e., the number of random bytes needed is smaller in our new countermeasure. Indeed, in the case where the nonlinear operation is built using the S-box of AES our new countermeasure needs less than 5 bytes of entropy whereas in the case of shuffle implementation 256 bytes are needed.²

The other important implementation parameter is the execution time of the table recomputation. In order to evaluate it, we implement in C a classical table recomputation without any countermeasure denoted by ${\text {TR}}$, a shuffled version denoted by ${\text {TRS}}$ where the permutation is drawn over all the possible permutations. We also implement our countermeasure in a naïve approach denoted by ${\text {TRCOMN}}$ and finally our countermeasure exploiting the cycle decomposition denoted by ${\text {TRCOM}}$. The summary of the different times of table recomputation execution can be found in Table 1. The profiling has been done using GPROF on an i5-6198DU CPU running at 2.30 GHz.

Table 1 Time needed for the table recomputation

It can be first noticed that the naïve approach leads to a prohibitive overhead, while the implementation using the cycle decomposition is computed in a reasonable supplementary amount of time. As a consequence, we can deduce that this countermeasure can be an interesting alternative to avoid the attacks presented in this article. Finally, the time needed to generate the random permutation is small. Indeed, both the implementation with and without shuffle have almost the same execution time. Nevertheless, these results may be slightly different on embedded systems where the random generation could be costly.

9 Conclusions and Perspectives

The table recomputation is a known weakness of masking schemes. We have recalled that practical countermeasures (e.g., shuffling with a high entropy) could be built to protect the table recomputation. In this article, we have presented a new multivariate attack exploiting the leakage of the protected table that outperformed classical HODPA even if a large amount of entropy is used to generate the countermeasure. This multivariate attack gives an example of a HODPA of nonminimal order which is more efficient than the corresponding minimal order HODPA. We have theoretically expressed the bound of noise in which this attack outperforms HOCPA using the ${\text {SNR}}$. Then, we have empirically validated this bound. Interestingly, we show that if the leakage model consists in a linear combination of bits, then our attack becomes all the better as the model gets further away from uniform weights (so-called Hamming weight model). Moreover, we have shown that the relative gain to use the multivariate attack grows linearly with the order of the masking schemes. This result highlights the fact that the study of masking scheme should take into account as second parameter the number of variables exploitable by these attacks. Indeed, we have shown in this article that when the number of variables used to perform the attacks increases, the order does not alone provide a criterion to evaluate the security of the countermeasure and that the SNR is a better security metric to consider.

In future works, we will investigate how to protect table recomputation against such attacks and investigate the cost of such countermeasures, evaluate the threat of such attacks on high-order masking schemes implemented on real components. We will also investigate how multivariate attacks could be applied on other masking schemes and protection techniques. And then, we will quantify the impact of these attacks.

Appendices

Proof of Theorem 3

In order to prove Theorem 3, let us first introduce some lemmas. By Remark 2 the only random parts of $X_{TR}$ are the noise and the mask. As a consequence the random variable $\left( X_{TR}| M=m \right)$ depends only on the noise, and is equal to:

$$\begin{aligned} \begin{aligned} \left( X_{TR}| M=m \right) =&-2 \times \frac{1}{2^n}\sum _{\omega = 0 }^{2^n -1 }\left[ \left( \mathsf {HW}[\varPhi \left( \omega \right) \oplus m ] + N_{\omega }^{(1)} - \frac{n}{2} \right) \right. \\&\quad \left. \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] + N_{\omega }^{(2)} - \frac{n}{2} \right) \right] . \end{aligned} \end{aligned}$$

(16)

Lemma 21

$$\begin{aligned} \begin{aligned} \left( X_{TR}| M=m \right) =&\mathsf {HW}[m ] - \frac{n}{2} \\&-2 \times \frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \right] \\&-2 \times \frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[ N_{\omega }^{(2)} \times \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ]-\frac{n}{2}\right) \right] \\&-2 \times \frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times N_{\omega }^{(2)} \right]. \end{aligned} \end{aligned}$$

(17)

Proof

$\left( X_{TR}| M=m \right)$ can be split into a deterministic part and a random part:

$$\begin{aligned} \left( X_{TR}| M=m \right)&= -2 \times \left( S_d + S_r \right) , \end{aligned}$$

where

$$\begin{aligned} S_d&= \frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[\left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ] -\frac{n}{2}\right) \times \left( \mathsf {HW}[ \varPhi \left( \omega \right) ] -\frac{n}{2} \right) \right] , \\ S_r&= \frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \right] \\&\quad +\,\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[ N_{\omega }^{(2)} \times \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ]-\frac{n}{2}\right) \right] \\&\quad +\,\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times N_{\omega }^{(2)} \right] .\\ S_d&{=} \mathbb {E}\left[\left( \mathsf {HW}[U \oplus M ] {-} \mathbb {E}\left[\mathsf {HW}[U \oplus M ] \right] \right) {\times } \left( \mathsf {HW}[U ]-\mathbb {E}\left[\mathsf {HW}[U \oplus M ] \right] \right) ~|~M{=}m \right] \\&= -\frac{1}{2}\mathsf {HW}[m ]+\frac{n}{4}\qquad \text {by}~[26]\ , \end{aligned}$$

where U denotes a random variable drawn uniformly over $\mathbb {F}_2^n$. $\square$

Lemma 22

$$\begin{aligned} \text {Var}\left[\left( X_{TR}| M=m \right) \right]= 4 \times \left( \frac{\sigma ^2}{2^n} \times \frac{n}{2} + \frac{\sigma ^4}{2^n} \right) . \end{aligned}$$

(18)

Proof

Recall that the random variable $\left( X_{TR}| M=m \right)$ can be write as in Lemma 21; thus $\text {Var}\left[\left( X_{TR}| M=m \right) \right]= 4 \times \left( V_1 + V_2 + V_3 + C_1 +C_2 + C_3 \right)$, where

$$\begin{aligned} V_1&= \text {Var}\left[\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \right] \right] , \\ V_2&= \text {Var}\left[\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(2)} \times \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ]-\frac{n}{2}\right) \right] \right] ,&\\ V_3&= \text {Var}\left[ \frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times N_{\omega }^{(2)} \right] \right],&\\ C_1&=2 \times \mathsf {Cov}\left[\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \right],\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times N_{\omega }^{(2)} \right] \right] ,&\\ C_2&= 2 \times \mathsf {Cov}\left[\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(2)} \times \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ]-\frac{n}{2}\right) \right],\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times N_{\omega }^{(2)} \right] \right] , \\ C_3&= 2 \times \mathsf {Cov} \biggl [ \frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \right] ,&\\&\qquad \quad \frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[ N_{\omega }^{(2)} \times \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ]-\frac{n}{2}\right) \right] \biggr ] . \end{aligned}$$

Let us now prove that $C_1=C_2=0$. First we have:

$$\begin{aligned} \mathsf {Cov}\left[\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \right],\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times N_{\omega }^{(2)} \right] \right] \! = \! C^{(1)}_1 - C^{(2)}_1 , \end{aligned}$$

with

$$\begin{aligned} C^{(1)}_1&= \mathsf {Cov}\left[\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[ \mathsf {HW}[\varPhi \left( \omega \right) ] \times N_{\omega }^{(1)} \right],\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times N_{\omega }^{(2)} \right] \right] \\&=\frac{1}{2^n}\sum _{\omega ' = 0}^{2^n-1} \frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[ \mathsf {Cov}\left[ \mathsf {HW}[\varPhi \left( \omega \right) ] \times N_{\omega }^{(1)} ,N_{\omega '}^{(1)} \times N_{\omega '}^{(2)} \right] \right] . \\ \end{aligned}$$

The random variables $N_{\omega }^{(i)}$, where $i\in \{1,2\}$ and $\omega \in \mathbb {F}_2^n$ are mutually independent and independent with all the $\mathsf {HW}[\varPhi \left( \omega \right) ]$. Thus we have:

$$\begin{aligned}&\forall \omega ,\omega ^{\prime } , \mathsf {Cov}\left[ \mathsf {HW}[\varPhi \left( \omega \right) ] \times N_{\omega }^{(1)} ,N_{\omega '}^{(1)} \times N_{\omega '}^{(2)} \right]=0 \\&\quad \iff \frac{1}{2^n}\sum _{\omega ' = 0}^{2^n-1} \frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[ \mathsf {Cov}\left[ \mathsf {HW}[\varPhi \left( \omega \right) ] \times N_{\omega }^{(1)} ,N_{\omega '}^{(1)} \times N_{\omega '}^{(2)} \right] \right] = 0 \\&\quad \iff C^{(1)}_1 =0. \end{aligned}$$

Besides

$$\begin{aligned} C^{(2)}_1&=\mathsf {Cov}\left[\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[ \frac{n}{2} \times N_{\omega }^{(1)} \right],\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times N_{\omega }^{(2)} \right] \right] \\&= \frac{n}{2} \times \frac{1}{2^n}\sum _{\omega ' = 0}^{2^n-1} \frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[ \mathsf {Cov}\left[ N_{\omega }^{(1)} ,N_{\omega '}^{(1)} \times N_{\omega '}^{(2)} \right] \right]. \end{aligned}$$

As $N_{\omega }^{(i)}$, where $i\in \{1,2\}$ and $\omega \in \mathbb {F}_2^n$, are mutually independent, we have:

$$\begin{aligned}&\mathsf {Cov}\left[N_{\omega }^{(1)},N_{\omega '}^{(1)} \times N_{\omega '}^{(2)} \right] = 0, ~ \forall \left( \omega ,\omega '\right) \in \mathbb {F}_2^n\times \mathbb {F}_2^n \\&\iff C^{(2)}_1 =\mathsf {Cov}\left[\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[ \frac{n}{2} \times N_{\omega }^{(1)} \right],\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times N_{\omega }^{(2)} \right] \right] = 0 \\&\iff \mathsf {Cov}\left[\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1}N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) ,\frac{1}{2^n}\sum _{\omega = 0}^{n-1}N_{\omega }^{(1)} \times N_{\omega }^{(2)} \right]=0. \end{aligned}$$

Identically we prove that:

$$\begin{aligned}&\mathsf {Cov}\left[\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[ N_{\omega }^{(2)} \times \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ]-\frac{n}{2}\right) \right],\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times N_{\omega }^{(2)} \right] \right] =0. \end{aligned}$$

As a consequence $C_1=C_2=0$. Let us now study $C_3$. By the bilinearity of the covariance $C_3$ can be rewritten such that:

$$\begin{aligned} C_3&\! = \! \frac{2}{2^{2n}}\sum _{\omega = 0}^{2^n-1} \sum _{\omega '= 0}^{2^n-1}\mathsf {Cov}\left[N_{\omega }^{(1)} \! \times \! \left( \mathsf {HW}[\varPhi \left( \omega \right) ] \! - \! \frac{n}{2} \right) ,N_{\omega '}^{(2)} \! \times \! \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ] \!- \!\frac{n}{2}\right) \right]. \end{aligned}$$

But

$$\begin{aligned}&\mathsf {Cov}\left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) ,N_{\omega '}^{(2)} \times \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ]-\frac{n}{2}\right) \right] \\&\qquad = \mathbb {E}\left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \times N_{\omega '}^{(2)} \times \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ]-\frac{n}{2}\right) \right]\\&\qquad - \mathbb {E}\left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \right] \times \mathbb {E}\left[N_{\omega '}^{(2)} \times \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ]-\frac{n}{2}\right) \right].\\ \end{aligned}$$

By definition, $N_{\omega }^{(1)}$ is independent from $\mathsf {HW}[\varPhi \left( \omega \right) ]$. Thus:

$$\begin{aligned}&\mathbb {E}\left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \right] = \mathbb {E}\left[N_{\omega }^{(1)} \right] \times \mathbb {E}\left[ \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \right] =0 \text { and} \\&\mathbb {E}\left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \right] \times \mathbb {E}\left[N_{\omega '}^{(2)} \times \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ]-\frac{n}{2}\right) \right]=0 . \end{aligned}$$

$N_{\omega }^{(1)}$ is independent from $\left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \times N_{\omega '}^{(2)}\times \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ]-\frac{n}{2}\right)$. Thus $\mathbb {E}\left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \times N_{\omega '}^{(2)} \times \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ]-\frac{n}{2}\right) \right] = 0$, which implies that $C_3=0$. As a consequence $\text {Var}\left[\left( X_{TR}| M=m \right) \right]= 4 \times \left( V_1 + V_2 + V_3 \right)$.

$$\begin{aligned} V_1&= \text {Var}\left[\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \right] \right] \nonumber \\&= \frac{1}{2^{2n}}\sum _{\omega = 0}^{2^n-1}\text {Var}\left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \right] \nonumber \\&\quad +\frac{2}{2^{2n}}\sum _{0 \leqslant \omega < \omega ' \leqslant 2^n -1}\mathsf {Cov}\left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] \right) ,N_{\omega '}^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega ' \right) ] \right) \right] . \end{aligned}$$

(19)

As $\mathsf {Cov}\left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] \right) ,N_{\omega '}^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega ' \right) ] \right) \right]=0$, the terms in Eq. (19) are all null. It can be noticed that $\mathbb {E}\left[\mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right]=0$ as $\varPhi \left( \omega \right)$ is uniformly distributed over $S_{2^n }$ and $\mathbb {E}\left[N_{\omega }^{(1)} \right]=0$. As a consequence:

$$\begin{aligned}&\text {Var}\left[N_{\omega }^{(1)} \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right) \right] = \text {Var}\left[ \mathsf {HW}[\varPhi \left( \omega \right) ] -\frac{n}{2} \right] \times \text {Var}\left[N_{\omega }^{(1)} \right] \text { , hence} \\&V_1 =\frac{1}{2^{2n}}\sum _{\omega = 0}^{2^n-1} \sigma ^2 \times \frac{n}{4} =\frac{1}{2^{n}}\times \sigma ^2 \times \frac{n}{4} . \end{aligned}$$

Identically, we have

$$\begin{aligned} V_2&= \text {Var}\left[\frac{1}{2^n}\sum _{\omega = 0}^{2^n-1} \left[N_{\omega }^{(2)} \times \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ]-\frac{n}{2}\right) \right] \right]=\frac{\sigma ^2}{2^n} \times \frac{n}{4} = V_1 \text { , and}\\ V_3&= \text {Var}\left[ \frac{1}{2^n}\sum _{\omega = 0}^{2^n-1}N_{\omega }^{(1)} \times N_{\omega }^{(2)} \right]=\frac{\sigma ^4}{2^n} . \end{aligned}$$

Finally

$$\begin{aligned} \text {Var}\left[\left( X_{TR}| M=m \right) \right]&= 4 \times \left( \frac{\sigma ^2}{2^n} \times \frac{n}{2} + \frac{\sigma ^4}{2^n} \right) . \end{aligned}$$

$\square$

Then, let us prove Theorem 3.

Proof

Lemma 22 gives us the value of the variance of the noise. Then by the definition of the ${\text {SNR}}$, we have:

$\square$

Proof of Propositions of Sect. 4.5

1.1 Proof of Proposition 5

Proof

By Theorem 2 in [16, Appendix A.2] (extended version of [15]), we have that the ${\text {SE}}$ of is given by

$$\begin{aligned} {\text {SE}}_{{\text {2O-CPA}}}&= \min _{k \ne k^{\star }} \frac{ \kappa \left( k^{\star },k \right) }{ 2 \left( \frac{\kappa '\left( k^{\star },k \right) }{\kappa \left( k^{\star },k \right) } - \kappa \left( k^{\star },k \right) \right) +2 \begin{array}{c} \sum \nolimits _{i\in \{0,2\}^d} \\ {i\ne (0, \ldots , 0)} \end{array} \prod _{1 \le \delta \le d} \left( \alpha _{\delta }^{-i_{\delta }} \cdot \sigma _{\delta }^{i_{\delta }} \right) } \\&= \min _{k \ne k^{\star }} \frac{ \kappa \left( k^{\star },k \right) }{ 2 \left( \frac{\kappa '\left( k^{\star },k \right) }{\kappa \left( k^{\star },k \right) } - \kappa \left( k^{\star },k \right) \right) +2 \left( \alpha _1 ^{-2} \sigma _1^2 + \alpha _2 ^{-2} \sigma _2^2 + \alpha _1 ^{-2} \sigma _1^2 \alpha _2 ^{-2} \sigma _2^2 \right) } . \end{aligned}$$

$\square$

1.2 Proof of Proposition 7

Proof

$$\begin{aligned} \frac{m_{{\text {2O-CPA}}}^{\left( {\text {SR}}\right) } - m_{{\text {MVA}}_{TR}}^{\left( {\text {SR}}\right) }}{m_{{\text {MVA}}_{TR}}^{\left( {\text {SR}}\right) }}&= \left( \frac{\log \left( 1 - {\text {SR}}\right) }{{\text {SE}}_{{\text {2O-CPA}}}} - \frac{\log \left( 1- {\text {SR}}\right) }{{\text {SE}}_{{\text {MVA}}_{TR}}}\right) \times \frac{{\text {SE}}_{{\text {MVA}}_{TR}}}{\log \left( 1- {\text {SR}}\right) } \\&= \frac{{\text {SE}}_{{\text {MVA}}_{TR}}}{{\text {SE}}_{{\text {2O-CPA}}}} - 1 , \end{aligned}$$

which indeed does not depend on ${\text {SR}}$. $\square$

1.3 Proof of Proposition 8

Let us now compute the difference of traces needed to reach any ${\text {SR}}$.

$$\begin{aligned} m_{{\text {2O-CPA}}}^{\left( {\text {SR}}\right) } - m_{{\text {MVA}}_{TR}}^{\left( {\text {SR}}\right) }&= \frac{\log \left( 1 - {\text {SR}}\right) }{{\text {SE}}_{{\text {2O-CPA}}}} - \frac{\log \left( 1- {\text {SR}}\right) }{{\text {SE}}_{{\text {MVA}}_{TR}}} \\ \end{aligned}$$

Let us rewrite using $\alpha = \alpha _1 = \alpha _2$. In such case:

$$\begin{aligned} m_{{\text {2O-CPA}}}^{\left( {\text {SR}}\right) } - m_{{\text {MVA}}_{TR}}^{\left( {\text {SR}}\right) }&= \frac{\log \left( 1 - {\text {SR}}\right) }{{\text {SE}}_{{\text {2O-CPA}}}} - \frac{\log \left( 1- {\text {SR}}\right) }{{\text {SE}}_{{\text {MVA}}_{TR}}} \\&= \frac{\log \left( 1 - {\text {SR}}\right) }{{\text {SE}}_{{\text {2O-CPA}}}} - \frac{\log \left( 1- {\text {SR}}\right) }{{\text {SE}}_{{\text {MVA}}_{TR}}} \\&= \left( 2 \alpha ^{-2} \frac{\log \left( 1 - {\text {SR}}\right) }{\kappa \left( k^{\star }, k \right) }\right) \left( 1 + \alpha ^{-2}\sigma ^2 \right) \left( \sigma ^2 - 4 \left( \frac{\sigma ^2}{2^n} \frac{n}{2} + \frac{\sigma ^4}{2^n} \right) \right) \end{aligned}$$

The attacks perform similarly when $m_{{\text {2O-CPA}}} - m_{{\text {MVA}}_{TR}} = 0$ which implies $(\sigma ^2 - 4 \times \left( \frac{\sigma ^2}{2^n} \times \frac{n}{2} + \frac{\sigma ^4}{2^n} \right) = 0$. Notice that we recover here the results of the Sect. 4.3.

In order to find the noise when the maximum occurs, let us compute the derivative in $\sigma ^2$:

$$\begin{aligned} \frac{ \mathrm {d}\left( m_{{\text {2O-CPA}}}^{\left( {\text {SR}}\right) } - m_{{\text {MVA}}_{TR}}^{\left( {\text {SR}}\right) } \right) }{\mathrm {d}\sigma ^2}&= \left( \left( \alpha ^{-2} - \frac{ 4 \alpha ^{-2}}{2^n} \times \frac{n}{2} \right) + \left( \frac{ 8 \alpha ^{-2}}{2^n} + 2\alpha ^{-4} - \frac{ 8 \alpha ^{-4}}{2^n} \times \frac{n}{2} \right) \sigma ^2 - \frac{ 12 \alpha ^{-4}\sigma ^4}{2^n} \right) \\&\qquad \times \left( 2 \frac{\log \left( 1 - {\text {SR}}\right) }{\kappa \left( k^{\star }, k \right) }\right) \end{aligned}$$

The maximum occurs when $\frac{ \mathrm {d}\left( m_{{\text {2O-CPA}}}^{\left( {\text {SR}}\right) } - m_{{\text {MVA}}_{TR}}^{\left( {\text {SR}}\right) } \right) }{\mathrm {d}\sigma ^2} = 0$ which not depends on the ${\text {SR}}$.

Proof of Theorem 10

Similarly to the Remark 2, we have $\forall i< d$:

$$\begin{aligned} \left( X_{CS_i^{d}} | M_i = m\right)&= \displaystyle {\frac{-2}{d 2^n} \sum _{\begin{array}{c} \omega \in \mathbb {F}_{2^n} \\ j \in \llbracket 1,d \rrbracket \end{array}}} \biggl [ \left( \mathsf {HW}[ \varPhi \left( \omega \right) \oplus m ] + N_{\left( \omega ,j \right) }^{(1)} -\frac{n}{2} \right) \\&\qquad \times \left( \mathsf {HW}[\varPhi \left( \omega \right) ] + N_{\left( \omega ,j \right) }^{(2)} -\frac{n}{2} \right) \biggr ] . \end{aligned}$$

As the i is fixed for each share we have removed it from the index position.

Lemma 23

$$\begin{aligned} \text {Var}\left[ \left( X_{CS_i^{d}} | M_i = m\right) \right]= 4 \times \left( \frac{\sigma ^2}{d \times 2^n} \times \frac{n}{2} + \frac{\sigma ^4}{d \times 2^n} \right) , \end{aligned}$$

(20)

where d is the number of share of the high-order masking scheme and $i<d$.

Proof

Lemma 23 is a straightforward extension of Lemma 22. $\square$

Exploiting Lemma 23, let us prove Theorem 10.

Proof

As Lemma 23 gives us the variance of the noise of the second-order leakage, we have $\forall i <d$

The upper bound of the interval are the $\sigma ^2$ where $\sigma ^2 \ne 0$ and:

$$\begin{aligned}&\frac{\sigma ^4}{d \times 2^{n-2}} = \left( d \times 2^{n-1} -n \right) \frac{\sigma ^2}{d \times 2^{n-1}} \\&\qquad \iff \sigma ^2 = \frac{ \left( d \times 2^{n-1} -n \right) }{2} \\&\qquad \iff \sigma ^2 = d \times 2^{n-2} - \frac{ n }{ 2} . \end{aligned}$$

It implies that the size of Useful Interval of Variance is given by $d \times 2^{n-2} - \frac{ n }{ 2}$. $\square$

Affine Model

1.1 Proof of Lemma 12

Proof

$$\begin{aligned}&\mathbb {E}\left[\left( \varPsi _{\alpha }\left( U \right) -\mathbb {E}\left[\varPsi _{\alpha }\left( U \right) \right] \right) \times \left( \varPsi _{\beta }\left( U \oplus z \right) -\mathbb {E}\left[\varPsi _{ \beta }\left( U \oplus z \right) \right] \right) \right] \\&\qquad =\mathbb {E}\left[ \left( \alpha \cdot U - \alpha \cdot \left( \frac{1}{2}\mathbf {1} \right) \right) \times \left( \beta \cdot \left( U \oplus z \right) - \beta \cdot \left( \frac{1}{2}\mathbf {1} \right) \right) \right]\\&\qquad = \mathbb {E}\left[ \left( \alpha \cdot \left( U - \frac{1}{2}\mathbf {1} \right) \right) \times \left( \beta \cdot \left( \left( U \oplus z \right) - \frac{1}{2}\mathbf {1} \right) \right) \right]\\&\qquad = \mathbb {E}\left[ \left( \frac{1}{2} \alpha \cdot \overline{ U } \right) \times \left( \frac{1}{2} \beta \cdot \left( \overline{ U \oplus z } \right) \right) \right] \\&\qquad =\frac{1}{4} \left( {\alpha }^\mathsf {t} \mathbb {E}\left[ \overline{ U } { \left( \overline{ U \oplus z } \right) }^\mathsf {t} \right] \beta \right) , \end{aligned}$$

where $\overline{U}$ denotes $2\left( U - \frac{1}{2} \mathbf {1} \right)$.

It can also be noticed that: $\overline{U} = -\bigl ( \left( -1 \right) ^{ U_1 },\ldots , \left( -1 \right) ^{ U_n } \bigr )$, and thus $\overline{ \left( U \oplus z \right) } = -\bigl ( \left( -1 \right) ^{ U_1+z_1 },\ldots , \left( -1 \right) ^{ U_n+z_n } \bigr )$. Moreover

$$\begin{aligned}&\mathbb {E}\left[ \overline{U} { \left( \overline{ U \oplus z } \right) }^\mathsf {t} \right] = \mathsf {Cov}\left[ \overline{U} , { \left( \overline{ U \oplus z } \right) }^\mathsf {t} \right] \\ \implies&\left( \mathbb {E}\left[ \overline{U} { \left( \overline{U \oplus z } \right) }^\mathsf {t} \right] \right) _{i,j} = \mathsf {Cov}\left[ \left( -1 \right) ^{ U_i }, \left( -1 \right) ^{\left( U_j + z_j \right) } \right] \\ \implies&\left( \mathbb {E}\left[ \overline{U} { \left( \overline{ U \oplus z } \right) }^\mathsf {t} \right] \right) _{i,j} = 0 \text { if }i \ne j \text { or } \left( \mathbb {E}\left[ \overline{U} { \left( \overline{ U \oplus z } \right) }^\mathsf {t} \right] \right) _{i,j} = \left( -1 \right) ^{ z_j } \text { if } i=j . \end{aligned}$$

Eventually, we have:

$$\begin{aligned}&\mathbb {E}\left[\left( \varPsi _{\alpha }\left( U \right) -\mathbb {E}\left[\varPsi _{\alpha }\left( U \right) \right] \right) \times \left( \varPsi _{\beta }\left( U \oplus z \right) -\mathbb {E}\left[\varPsi _{ \beta }\left( U \oplus z \right) \right] \right) \right] \\&\qquad =- \frac{1}{4} \left( \alpha \odot \beta \right) \cdot \overline{z} =- \frac{1}{4} \left( \alpha \odot \beta \right) \cdot 2 \left( z - \frac{1}{2}\mathbf {1} \right) \\&\qquad =-\frac{1}{2} \left( \alpha \odot \beta \right) \cdot z + \frac{1}{4} \left( \alpha \odot \beta \right) \cdot \mathbf {1} =-\frac{1}{2} \left( \alpha \odot \beta \right) \cdot z + \frac{1}{4} \alpha \cdot \beta . \end{aligned}$$

$\square$

1.2 Proof of Theorem 15

Similarly to Eq. (16), we have:

$$\begin{aligned} \left( X_{TR}| M=m \right) =&-2 \times \frac{1}{2^n}\sum _{\omega = 0 }^{2^n -1 }\biggl [\left( \alpha \cdot \left( \varPhi \left( \omega \right) \oplus m \right) + N_{\omega }^{(1)} - \frac{1}{2}\left( \alpha \cdot \mathbf {1} \right) \right) \\&\qquad \times \left( \alpha \cdot \left( \varPhi \left( \omega \right) \right) + N_{\omega }^{(2)} - \frac{1}{2}\left( \alpha \cdot \mathbf {1} \right) \right) \biggr ]. \end{aligned}$$

Lemma 24

$$\begin{aligned} \text {Var}\left[\left( X_{TR}| M=m \right) \right]= 4 \times \left( \frac{n}{2^{n+1}} \times \sigma ^2 + \frac{\sigma ^4}{2^n} \right) . \end{aligned}$$

Proof

Similar to proof of Lemma 22 (see “Appendix A”) using the affine model instead of the Hamming Weight and Assumption 1. $\square$

Then, we can prove Theorem 15.

Proof

Lemma 24 gives us the value of the variance of the noise. Then by the definition of the ${\text {SNR}}$, we have:

$\square$

1.3 Proof of Corollary 16

Let us first prove the following result:

Lemma 25

Let $x \in \mathbb {R}^n$ and let p, q two integers such that $p> q > 0$. Then:

$$\begin{aligned} n^{\frac{1}{p}-\frac{1}{q}} \, ||{x}||_{q} \leqslant ||{x}||_{p} \leqslant ||{x}||_{q} . \end{aligned}$$

(21)

These two bounds are tight. Indeed,

$$\begin{aligned}&\forall i,j, x_i =x_ j&\implies n^{\frac{1}{p}-\frac{1}{q}} ||{x}||_{q} = ||{x}||_{p} \\&\exists i / x_i \ne 0 \text { and } \forall i \ne j, x_j=0&\implies ||{x}||_{p} = ||{x}||_{q} . \end{aligned}$$

Proof

Let us first prove the lower bound of Eq. (21). By the Hölder inequality we have:

$$\begin{aligned}&\sum _i |x_i|^q \leqslant \left( \sum _i (|x_i|^q )^P \right) ^\frac{1}{P} \left( \sum _i \left( 1\right) ^Q \right) ^\frac{1}{Q} \text {where } P = \frac{p}{q} \text { and } Q = \frac{p}{p-q} . \end{aligned}$$

So, we have, $\sum _i |x_i|^q \leqslant ||{x}||_{p}^q n^{1-\frac{q}{p}}$, i.e., $||{x}||_{p} n^{\frac{1}{p}-\frac{1}{q}} \leqslant ||{x}||_{p}$.

Then, let us prove the upper bound. We have $\sum _i \frac{|x_i|^q }{||{x}||_{q}^q} =1$. Hence, for all $1\leqslant i\leqslant n$, $\frac{|x_i|^q }{||{x}||_{q}^q} \leqslant 1$. Therefore, for all i, $\frac{|x_i|^p }{||{x}||_{q}^{p}} \leqslant \frac{|x_i|^q }{||{x}||_{q}^q}$, hence $\sum _i \frac{|x_i|^p }{||{x}||_{q}^{p}} \leqslant \sum _i \frac{|x_i|^q }{||{x}||_{q}^q} = 1$, which yields the announced inequality: $||{x}||_{p}^p \leqslant ||{x}||_{q}^{p}$.

Let us prove the sufficient conditions when the inequalities become equalities:

$$\begin{aligned} \forall i,j, x_i =x_ j \implies ||{x}||_{p} = |x_i| n^{\frac{1}{p}} \text { and } ||{x}||_{q} = |x_i| n^{\frac{1}{q}} \implies ||{x}||_{p} = ||{x}||_{q} n^{\frac{1}{p}- \frac{1}{q}} \\ \exists i, x_i \ne 0 \text { and } \forall i \ne j, x_j=0 \implies ||{x}||_{p} = |x_i| \text { and } ||{x}||_{q} = |x_i| \implies ||{x}||_{p} = ||{x}||_{q} . \end{aligned}$$

$\square$

The Corollary 16 is the application of Lemma 25 with $p=4$ and $q=2$.

Proof

Indeed, we have by Theorem 15 that the useful interval of variance is $0 \leqslant \sigma ^2 \leqslant ||{\alpha }||_{4}^4 \times \frac{2^{n-2}}{n} - \frac{n}{2}$, where $||{\alpha }||_{2}^2=n$ (recall Assumption 1). Then, by Lemma 25:

$$\begin{aligned}&\left( ||{\alpha }||_{2}n^{\frac{1}{4}-\frac{1}{2} +\frac{1}{2} } \right) ^4 \times \frac{2^{n-2}}{n} - \frac{n}{2} \leqslant ||{\alpha }||_{4}^4 \times \frac{2^{n-2}}{n} - \frac{n}{2} \leqslant ||{\alpha }||_{2}^4 \times \frac{2^{n-2}}{n} - \frac{n}{2} \\ \implies&\left( ||{\alpha }||_{2}n^{\frac{1}{4}-\frac{1}{2}} \right) ^4 \times \frac{2^{n-2}}{n} - \frac{n}{2} \leqslant ||{\alpha }||_{4}^4 \times \frac{2^{n-2}}{n} - \frac{n}{2} \leqslant n^2 \times \frac{2^{n-2}}{n} - \frac{n}{2} \\ \implies&\underbrace{2^{n-2} - \frac{n}{2}}_{\text {Value of Theorem}~3.} \leqslant ||{\alpha }||_{4}^4 \times \frac{2^{n-2}}{n} - \frac{n}{2} \leqslant n \times 2^{n-2}- \frac{n}{2} \end{aligned}$$

$\square$