Skip to main content
SpringerLink
Log in

Next-best-view regression using a 3D convolutional neural network

  • Original Paper
  • Published:
Machine Vision and Applications Aims and scope Submit manuscript

Abstract

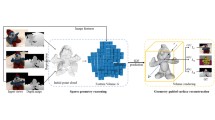
Automated three-dimensional (3D) object reconstruction is the task of building a geometric representation of a physical object by means of sensing its surface. Even though new single-view reconstruction techniques can predict the surface, they lead to incomplete models, specially, for non-commons objects such as antique objects or art sculptures. Therefore, to achieve the task’s goals, it is essential to automatically determine the locations where the sensor will be placed so that the surface will be completely observed. This problem is known as the next-best-view problem. In this paper, we propose a data-driven approach to address the problem. The proposed approach trains a 3D convolutional neural network (3D CNN) with previous reconstructions in order to regress the position of the next-best-view. To the best of our knowledge, this is one of the first works that directly infers the next-best-view in a continuous space using a data-driven approach for the 3D object reconstruction task. We have validated the proposed approach making use of two groups of experiments. In the first group, several variants of the proposed architecture are analyzed. Predicted next-best-views were observed to be closely positioned to the ground truth. In the second group of experiments, the proposed approach is requested to reconstruct several unseen objects, namely, objects not considered by the 3D CNN during training nor validation. Coverage percentages of up to 90 % were observed. With respect to current state-of-the-art methods, the proposed approach improves the performance of previous next-best-view classification approaches and it is quite fast in running time (3 frames per second), given that it does not compute the expensive ray tracing required by previous information metrics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Scott, W., Roth, G., Rivest, J.: View planning for automated three-dimensional object reconstruction and inspection. ACM Comput. Surv. 35, 64–96 (2003). https://doi.org/10.1145/641865.641868

    Article  Google Scholar 

  2. Jovančević, I., Larnier, S., Orteu, J.J., Sentenac, T.: Automated exterior inspection of an aircraft with a pan-tilt-zoom camera mounted on a mobile robot. J. Electron. Imaging 24(6), 061110 (2015)

    Article  Google Scholar 

  3. Themistocleous, K., Ioannides, M., Agapiou, A., Hadjimitsis, D.G.: The methodology of documenting cultural heritage sites using photogrammetry, uav, and 3d printing techniques: the case study of asinou church in cyprus. In: Third International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2015), vol. 9535. International Society for Optics and Photonics (2015)

  4. Mur-Artal, R., Montiel, J.M.M., Tardos, J.D.: ORB-SLAM: a versatile and accurate monocular SLAM system. IEEE Trans. Robot. 31(5), 1147–1163 (2015). https://doi.org/10.1109/TRO.2015.2463671

    Article  Google Scholar 

  5. Martinez-Carranza, J., Calway, A., Mayol-Cuevas, W.: Enhancing 6d visual relocalisation with depth cameras. In: Intelligent Robots and Systems (IROS), 2013 IEEE/RSJ International Conference on, pp. 899–906. IEEE (2013)

  6. Chen, S., Li, Y., Kwok, N.M.: Active vision in robotic systems: a survey of recent developments. Int. J. Robot. Res. 30(11), 1343–1377 (2011)

    Article  Google Scholar 

  7. Connolly, C.: The determination of next best views. In: Proceedings IEEE International Conference on Robotics and Automation, vol. 2, pp. 432–435. St. Louis, MO, USA (1985)

  8. Delmerico, J., Isler, S., Sabzevari, R., Scaramuzza, D.: A comparison of volumetric information gain metrics for active 3d object reconstruction. Autonomous Robots 42(2), 197–208 (2018)

    Article  Google Scholar 

  9. Vasquez-Gomez, J.I., Sucar, L.E., Murrieta-Cid, R.: View/state planning for three-dimensional object reconstruction under uncertainty. Autonomous Robots 41(1), 89–109 (2017)

    Article  Google Scholar 

  10. Doumanoglou, A., Kouskouridas, R., Malassiotis, S., Kim, T.K.: Recovering 6d object pose and predicting next-best-view in the crowd. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 3583–3592 (2016)

  11. Monica, R., Aleotti, J.: Contour-based next-best view planning from point cloud segmentation of unknown objects. Autonomous Robots 42(2), 443–458 (2018)

    Article  Google Scholar 

  12. Chen, S., Li, Y.: Vision sensor planning for 3-d model acquisition. IEEE Trans. Syst. Man Cybern. 35(5), 894–904 (2005)

    Article  Google Scholar 

  13. Mendoza, M., Vasquez-Gomez, J.I., Taud, H., Sucar, L.E., Reta, C.: Supervised learning of the next-best-view for 3d object reconstruction. Pattern Recognition Letters (2020)

  14. Zeng, R., Zhao, W., Liu, Y.J.: Pc-nbv: A point cloud based deep network for efficient next best view planning. In: 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (2020)

  15. Mendoza, M., Vasquez-Gomez, J.I., Taud, H.: Nbv regression dataset. https://github.com/irvingvasquez/nbv-regression-dataset (2018). [Online; accessed 20-January-2019]

  16. Song, S., Jo, S.: Online inspection path planning for autonomous 3d modeling using a micro-aerial vehicle. In: 2017 IEEE International Conference on Robotics and Automation (ICRA), pp. 6217–6224. IEEE (2017)

  17. Kriegel, S., Rink, C., Bodenmüller, T., Narr, A., Suppa, M., Hirzinger, G.: Next-best-scan planning for autonomous 3d modeling. In: 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 2850–2856. IEEE (2012)

  18. Zeng, R., Wen, Y., Zhao, W., Liu, Y.J.: View planning in robot active vision: a survey of systems, algorithms, and applications. Comput. Vis. Media 6(3), 225–245 (2020)

    Article  Google Scholar 

  19. Torabi, L., Gupta, K.: An autonomous six-dof eye-in-hand system for in situ 3d object modeling. Int. J. Robot. Res. 31(1), 82–100 (2012)

    Article  Google Scholar 

  20. Kriegel, S., Rink, C., Bodenmüller, C., Suppa, M.: Efficient next-best-scan planning for autonomous 3d surface reconstruction of unknown objects. J. Real-Time Image Process. 10, 611–631 (2015)

  21. Kavraki, L.E., Svestka, P., Latombe, J.C., Overmars, M.H.: Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 12(4), 566–580 (1996)

    Article  Google Scholar 

  22. S.M., Kuffner, J.J.: Randomized kinodynamic planning. Int. J. Robot. Res. 20(5), 378–400 (2001). https://doi.org/10.1177/02783640122067453

  23. Khalfaoui, S., Seulin, R., Fougerolle, Y.D., Fofi, D.: An efficient method for fully automatic 3d digitization of unknown objects. Comput. Ind. 64(9), 1152–1160 (2013)

    Article  Google Scholar 

  24. Potthast, C., Sukhatme, G.: A probabilistic framework for next best view estimation in a cluttered environment. J. Vis. Comun. Image Represent 25(1), 148–164 (2014)

    Article  Google Scholar 

  25. Lauri, M., Pajarinen, J., Peters, J., Frintrop, S.: Multi-sensor next-best-view planning as matroid-constrained submodular maximization. IEEE Robot. Autom. Lett. 5(4), 5323–5330 (2020)

    Article  Google Scholar 

  26. Song, S., Jo, S.: Surface-based exploration for autonomous 3d modeling. In: IEEE International Conference on Robotics and Automation, pp. 4319–4326. IEEE (2018)

  27. Hardouin, G., Morbidi, F., Moras, J., Marzat, J., Mouaddib, E.M.: Surface-driven next-best-view planning for exploration of large-scale 3d environments. In: 21st IFAC World Congress (VIRTUEL) (2020)

  28. Ramanagopal, M.S., Nguyen, A.P.V., Ny, J.L.: A motion planning strategy for the active vision-based mapping of ground-level structures. IEEE Trans. Autom. Sci. Eng. 15(1), 356–368 (2018)

    Article  Google Scholar 

  29. Moritani, R., Kanai, S., Date, H., Niina, Y., Honma, R.: Plausible reconstruction of an approximated mesh model for next-best view planning of sfm-mvs. Int. Archives Photogramm. Remote Sens. Spat. Inf. Sci. 43, 465–471 (2020)

  30. Wu, Z., Song, S., Khosla, A., Yu, F., Zhang, L., Tang, X., Xiao, J.: 3d shapenets: A deep representation for volumetric shapes. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 1912–1920 (2015)

  31. Johns, E., Leutenegger, S., Davison, A.J.: Pairwise decomposition of image sequences for active multi-view recognition. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 3813–3822 (2016)

  32. Hepp, B., Dey, D., Sinha, S.N., Kapoor, A., Joshi, N., Hilliges, O.: Learn-to-score: Efficient 3d scene exploration by predicting view utility. In: Proceedings of the European Conference on Computer Vision (ECCV), pp. 437–452 (2018)

  33. Bai, S., Chen, F., Englot, B.: Toward autonomous mapping and exploration for mobile robots through deep supervised learning. In: 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 2379–2384. IEEE (2017)

  34. Julian, B.J., Karaman, S., Rus, D.: On mutual information-based control of range sensing robots for mapping applications. Int. J. Robot. Res. 33(10), 1375–1392 (2014)

    Article  Google Scholar 

  35. Wang, Y., James, S., Stathopoulou, E.K., Beltrán-González, C., Konishi, Y., Del Bue, A.: Autonomous 3-d reconstruction, mapping, and exploration of indoor environments with a robotic arm. IEEE Robot. Automation Lett. 4(4), 3340–3347 (2019). https://doi.org/10.1109/LRA.2019.2926676

    Article  Google Scholar 

  36. Wu, C., Zeng, R., Pan, J., Wang, C.C., Liu, Y.J.: Plant phenotyping by deep-learning-based planner for multi-robots. IEEE Robot. Automation Lett. 4(4), 3113–3120 (2019)

    Article  Google Scholar 

  37. Yuan, W., Khot, T., Held, D., Mertz, C., Hebert, M.: Pcn: Point completion network. In: 2018 International Conference on 3D Vision (3DV), pp. 728–737. IEEE (2018)

  38. Besl, P., McKay, N.: A method for registration of 3-d shapes. IEEE Trans. Pattern Anal. Mach. Intell. 14, 239–256 (1992). https://doi.org/10.1109/34.121791

    Article  Google Scholar 

  39. Hornung, A., Wurm, K.M., Bennewitz, M., Stachniss, C., Burgard, W.: OctoMap: an efficient probabilistic 3D mapping framework based on octrees. Autonomous Robots (2013). https://doi.org/10.1007/s10514-012-9321-0

    Article  Google Scholar 

  40. Thrun, S., Burgard, W., Fox, D.: Probabilistic robotics. The MIT Press, Cambridge (2005)

    MATH  Google Scholar 

  41. Mendoza, M., Vasquez-Gomez, J.I., Taud, H.: Nbv classification dataset. https://www.kaggle.com/miguelmg/nbv-dataset (2018). [Online; accessed 20-January-2019]

  42. Kingma, D.P., Ba, J.: Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014)

  43. Gschwandtner, M., Kwitt, R., Uhl, A., Pree, W.: Blensor: Blender sensor simulation toolbox. In: International Symposium on Visual Computing, pp. 199–208. Springer (2011)

Download references

Author information

Authors and Affiliations

  1. Consejo Nacional de Ciencia y Tecnología (CONACYT), Insituto Politécnico Nacional, México City, México

    J. Irving Vasquez-Gomez

  2. Consejo Nacional de Ciencia y Tecnología (CONACYT) - Escuela Superior de Cómputo (ESCOM), Instituto Politécnico Nacional (IPN), México City, México

    David Troncoso

  3. Consejo Nacional de Ciencia y Tecnología (CONACYT) - Centro de, Investigación en Matemáticas CIMAT, Guanajuato, México

    Israel Becerra

  4. Instituto Nacional de Astrofísica Óptica y Electrónica (INAOE), Puebla, México

    Enrique Sucar

  5. Centro de Investigación en Matemáticas CIMAT, Guanajuato, México

    Rafael Murrieta-Cid

Authors
  1. J. Irving Vasquez-Gomez
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. David Troncoso
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Israel Becerra
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Enrique Sucar
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Rafael Murrieta-Cid
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. Irving Vasquez-Gomez.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was partially supported by CONACYT-cátedra 1507 project.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vasquez-Gomez, J.I., Troncoso, D., Becerra, I. et al. Next-best-view regression using a 3D convolutional neural network. Machine Vision and Applications 32, 42 (2021). https://doi.org/10.1007/s00138-020-01166-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00138-020-01166-2

Keywords

Search

Navigation