1 Introduction

Nowadays, because the application of simulations reduces the execution time and materials used, the structural modelling has become a more important tool for designers, engineers and architects. Therefore, knowledge of the mechanical properties along all major axes of wood has become more essential. In the case of wood, considered in a simplified form as an orthotropic solid, full characterization of its elastic behavior requires the determination of twelve independent elastic parameters: three Young’s moduli (E L, E R, and E T), three shear moduli (G LR, G LT, and G RT), and six Poisson ratios (\({\nu _{{\text{LR}}}},\) \({\nu _{{\text{LT}}}},\) \({\nu _{{\text{RL}}}},\) \({\nu _{{\text{RT}}}},\) \({\nu _{{\text{TL}}}}\) and \({\nu _{{\text{TR}}}}\)) (Bodig and Jayne 1982). However, in China, most reports regarding the elastic properties of wood commonly include only values for the elastic modulus in the longitudinal direction. The main reasons for that are attributed to two aspects. On the one hand, the elastic modulus in longitudinal direction is most commonly used for determining structural dimensions; on the other hand, the determination of the shear modulus in the three principle planes of symmetry and the elastic modulus in the radial and tangential directions is more difficult when using standard static tests. Furthermore, almost no information about the Poisson ratios is available. Therefore, comprehensive data sets of the elastic constants in the three principle directions and the three principal planes are still lacking for most Chinese domestic species.

In many literature references, a combination of ultrasonic and static experimentally determined elastic properties is described (Keunecke et al. 2007, 2008; Niemz and Caduff 2008; Ozyhar et al. 2013a; Gonçalves et al. 2011, 2014; Vázquez et al. 2015). On the one hand, using ultrasonic wave propagation for determining elastic properties of wood is now well accepted and frequently used (Keunecke et al. 2007, 2011; Gonçalves et al. 2011, 2014; Ozyhar et al. 2013b; Vázquez et al. 2015). This method is usually applied to determine the Young’s moduli (E L, E R, and E T) and the shear moduli (G LR, G LT, and G RT) of wood. The advantages of the ultrasonic technique for determination of wood properties are attributed to the possibility of non-destructive testing the same specimen several times, and the capability to test small specimens and thus reducing the influence of growth ring curvature (Keunecke et al. 2007). On the other hand, by using static tests (compression or tension) combined with digital image correlation (DIC) method to obtain strain information, the Young’s moduli (E L, E R, and E T) and Poisson ratios (\({\nu _{{\text{LR}}}},\) \({\nu _{{\text{LT}}}},\) \({\nu _{{\text{RL}}}},\) \({\nu _{{\text{RT}}}},\) \({\nu _{{\text{TL}}}}\) and \({\nu _{{\text{TR}}}}\)) have been determined for some species (Keunecke et al. 2008; Hering et al. 2012; Ozyhar et al. 2012, 2013a; Niemz et al. 2014; Clauss et al. 2014).

It is a fact that if all terms of the stiffness matrix [C] obtained by ultrasound using the Christoffel’s equations are known, the calculation of compliance matrix [S] can be performed using the inverse matrix [C]−1. With the [S] matrix, it is possible to determine the three Young’s moduli (E L, E R, and E T), the three shear moduli (G LR, G LT, and G RT), and the six Poisson ratios (\({\nu _{{\text{LR}}}},\) \({\nu _{{\text{LT}}}},\) \({\nu _{{\text{RL}}}},\) \({\nu _{{\text{RT}}}},\) \({\nu _{{\text{TL}}}}\) and \({\nu _{{\text{TR}}}}\)). However, some researchers indicated that the stiffness coefficients C LL, C RR, and C TT obtained by the ultrasonic technique without considering the complete stiffness matrix tend to deliver higher values than Young’s moduli E L, E R, and E T obtained in static tests, as the difference between stiffness coefficients and Young’s moduli is a combination of Poisson ratio from the matrix inversion (Sinclair and Farshad 1987; Oliveira et al. 2002; Bucur 2006; Keunecke et al. 2007; Gonçalves et al. 2011; Ozyhar et al. 2013b). Sinclair and Farshad (1987) demonstrated that the ultrasonic test produced values for the longitudinal elasticity modulus 73% higher than the static test and attributed these differences to the fact that E L was calculated directly by C LL and not by the complete expression that would involve Poisson ratio. Bucur (2006) stated that the C LL was 22% higher than E L obtained by the static test for Douglas fir, while for Sitka spruce, where E L was calculated through the complete stiffness matrix, the E L value was only 5% higher than that obtained by the static test. In the research by Gonçalves et al. (2011), the values for the stiffness coefficients were even greater than those for the static moduli. However, when the values of stiffness coefficients were corrected by the Poisson ratio, the difference was reduced and the elastic parameters obtained by ultrasound showed values only slightly higher than those obtained statically. Ozyhar et al. (2013b) also revealed that the stiffness coefficients calculated without taking the non-diagonal terms of the stiffness matrix into account results in highly overestimated values compared with the Young’s moduli obtained from the static test. While in the case of the Young’s moduli calculated through the complete stiffness matrix, the ultrasonic Young’s moduli in the radial and tangential direction were in good agreement with the Young’s moduli obtained by static test, the ultrasonic longitudinal Young’s moduli were found to be 20–30% lower compared with the static ones. Furthermore, according to Gonçalves et al. (2014), when comparing ultrasonic wave propagation tests and static tests, the static tests are conducted by an isothermal process, whereas dynamic testing is conducted by an adiabatic process. In the isothermal process, the internal energy of the material neither increases nor decreases, while in the adiabatic process, there is an increase in the internal energy of the materials. For this reason, even if the stiffness matrix is completely established by ultrasound and all elastic constants of wood are calculated from this matrix, the absolute values obtained by ultrasound are expected to be greater than those obtained by static testing.

Therefore, the main goals of this study are to evaluate the three-dimensional elastic behavior (e.g., stiffness coefficients: C LL, C RR, and C TT) of Chinese fir wood using ultrasonic wave propagation method, and to compare the results with the Young’s moduli (E L, E R, and E T) obtained by static compression and tension tests. The influence of the moisture content on the elastic properties was also determined. Furthermore, the effect of a correction with the Poisson ratio on the stiffness coefficients is clarified, and the differences of elastic parameters obtained by ultrasound and static tests are revealed.

2 Materials and methods

2.1 Raw material

Chinese fir [Cunninghamia lanceolata (Lamb.) Hook] plantation wood was tested. The average raw density, determined at a temperature of 20 °C and a relative humidity (RH) of 65%, is about 323 kg/m3. All test specimens were cut from the heartwood part of the same trunk. All knots or defects in the wood structure were excluded in advance from testing.

2.2 Specimen preparation for ultrasound testing

The clear cubic specimens with orthotropic material directions parallel to the sample edges were prepared, with edge length of 10, 13 and 16 mm, respectively. For each thickness set, cubes were successively cut from a stick perfectly parallel to the longitudinal direction. This precaution allows the same annual growth rings to be tested, and yields a series of matched samples with very similar properties. To achieve a precise surface area for ultrasonic testing, cubes were finished with fine sandpaper. Prior to testing, specimens were divided into four groups and moisture-conditioned in climatic chambers at a temperature of 20 °C and different relative humidity of 50, 65, 85 and 95% until equilibrium moisture content was reached. A total of 240 specimens with 20 specimens for each dimension and moisture condition were available for testing.

2.3 Measurement of ultrasound velocity

Ultrasound testing was performed with an Epoch XT ultrasonic flaw detector (Olympus NDT Inc., USA). For determining the stiffness constants, longitudinal waves with a frequency of 2.27 MHz were generated with an Olympus A133S transducer (diameter 12.0 mm). A pair of selected transducers was used: one of them being the emitter and the other one the receiver. Specimens were fixed using a clamping apparatus that ensured constant contact pressure and the gel-like coupling medium (Ultragel II) was used to ensure good coupling.

From the ultrasound runtime (t) and the length of ultrasound propagation in grain orientation direction (L i), the sound velocity (\({V_{\text{i}}}\)) was calculated according to Eq. (1).

$${V_i}=\frac{{{L_i}}}{t}\quad i \in L,R,T$$
(1)

As a result, three sound velocities (\({V_{\text{L}}}\), \({V_{\text{R}}}\) and \({V_{\text{T}}}\)) were obtained with longitudinal wave propagating along the L, R and T directions, respectively.

The received signal was recorded at a sampling frequency of 100 MHz. The peak of the first received signal was amplified to 100% of the display scale and the delay of the signal was measured at the flank of the corresponding incoming wave at 30% of the display scale. For the calculation of the ultrasound velocity, it has to be taken into consideration that besides the specimen itself, the sound waves have to propagate through the protective layer covering the oscillator of the transducer and through the coupling medium as well. Thus, to eliminate the sound velocity error introduced by the flaw detector, the resulting sound velocities were determined by a simple linear regression from the measured time required for the ultrasound pulse to propagate through the aforementioned samples with three different thicknesses (Fig. 1).

Fig. 1
figure 1

Ultrasound wave velocity determination from the measured ultrasound propagation time and specific sample thickness

Full size image

2.4 Calculation of stiffness coefficients

On the basis of the propagation velocity (\({V_i}\)) of the ultrasonic waves and of the raw density (\(\rho\)) of the specimens, the stiffness coefficient (\({C_{ii}}\)) was calculated according to Eq. (2):

$${C_{ii}}=\rho V_{i}^{2}\quad i \in L,R,T$$
(2)

However, it should be noted that, when applying ultrasonic techniques for determining the stiffness coefficients, velocities have to be measured along the orthotropic axes and at various angles with these axes as well (explained in detail in Bucur and Archer 1984). This method is quite complex and the necessary specimen preparation and measuring require much effort. Therefore, a frequent approach is to use a simplified equation (Eq. 2) for calculating the stiffness coefficients.

2.5 Specimen preparation for compression and tension

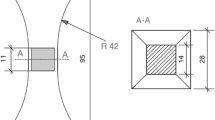
A dog-bone shaped specimen, as presented in Fig. 2, was used for the compression and tension tests. The cross-sectional area in the narrow specimen section was 14 mm × 14 mm with parallel specimen surfaces and with a length of 11 mm in the load direction. The matching of the specimen coordinate system and the principle orientation of the wooden material in the load area was ensured. A total of 240 specimens were divided into four groups with 20 samples per load axes L, R and T; each group was conditioned in climatic chambers at 50, 65, 85 and 95% RH and a temperature of 20 °C.

Fig. 2
figure 2

Dog-bone shaped specimen used to determine the elastic properties by both compression and tension testing. Figure showing the optical analyzed area is displayed in gray. The dimensions are in (mm)

Full size image

2.6 Speckle pattern

A high-contrast random dot texture (“speckle pattern”) was sprayed onto two adjacent sides of the waisted specimen section (11 mm × 14 mm, Fig. 2). An airbrush gun and finely pigmented acrylic paint was used to obtain very fine speckles and therefore a high-resolution pattern. First, a white ground coat and then black speckles were applied, resulting in a speckle pattern of heterogeneous grey values. These patterns were needed for the evaluation of strains at the specimen surface during compression or tension tests by means of DIC software.

2.7 Compression and tension tests

After the specimens reached equilibrium moisture content, compression and tension tests were respectively performed using a Zwick Z100 (Zwick GmbH & Co. KG, Ulm, Germany) universal testing machine equipped with a 100 kN load cell. Data acquisition began when a defined preload was reached. A displacement controlled test was performed with a testing speed of about 1 mm/min. In the compression tests, a flexible joint was used to prevent bending and to compensate for possible non-parallel planes due to small dimensional changes as a result of climatisation. As for tension tests, the central load transmission for both configurations was achieved with conical clamp jaws. To determine the Young’s moduli and Poisson ratios, both the compression and tension tests were performed only at small strains in the linear elastic range.

2.8 Strain measurement

For the strain measurement, an optical video image correlation system (VIC 2D, Correlated Solutions Inc., Columbia, SC, USA) was applied that allows an evaluation of the strain distribution over the complete specimen surface. For this purpose, an optimized correlation algorithm was available, which provided full-field displacement and strain data for mechanical testing on planar specimens. The displacement data from two adjacent sides of the specimen during both the compression and tension measurements were determined by a pair of charge coupled device (CCD) digital cameras, each with a maximum resolution of 2048 × 2048 pixels. The in-plane movement was determined for the selected measurement area of interest with a size of about 11 mm × 11 mm (Fig. 2) by calculating the average strain in the load direction and across this direction.

2.9 Calculation of Young’s moduli

The Young’s moduli E were obtained from the ratio of the stress \({{\varvec{\upsigma}}}\) to the corresponding strain ε measured in the linear elastic range

$${E_i}=\frac{{\Delta {\sigma _i}}}{{\Delta {\varepsilon _i}}}=\frac{{{\sigma _{i,2}} - {\sigma _{i,1}}}}{{{\varepsilon _{i,2}} - {\varepsilon _{i,1}}}}\quad i \in L,R,T$$
(3)

The specific stress-boundaries, \({\sigma _{i,1}}\) and \({\sigma _{i,2}}\), were set at 30 and 70% of the actual force at 50% elastic limit. The orientation dependent maximum forces were determined in the preliminary tests for the three main directions.

2.10 Calculation of Poisson ratios

The Poisson ratio \(\nu ,\) defined as the strain ratio of the passive (lateral) strain component \({\varepsilon _i}\) and the active (axial) strain component in the load direction \({\varepsilon _j}\)

$${\nu _{ij}}= - \frac{{{\varepsilon _i}}}{{{\varepsilon _j}}}\quad i,j \in L,R,T\;{\text{and}}\;i \ne j$$
(4)

were determined in the linear elastic range from the linear regression of the passive–active strain diagram.

2.11 Calculation of equilibrium moisture content

For the calculation of the equilibrium moisture content ω (Eq. 5), the mass of the samples was determined at 20 °C and 50, 65, 85, 95% RH (m ω) and oven-dry (m 0):

$$\omega ={{\left( {{m_\omega } - {m_0}} \right)} \mathord{\left/ {\vphantom {{\left( {{m_\omega } - {m_0}} \right)} {{m_0}}}} \right. \kern-0pt} {{m_0}}} \times 100\%$$
(5)

The corresponding equilibrium moisture contents were 10.3, 12.2, 14.6 and 16.7%, respectively.

2.12 Statistical analysis

Duncan’s multiple range tests and linear regression for variable were applied in this study.

3 Results and discussion

3.1 Velocity of ultrasonic waves in three principle directions

Table 1 summarizes the results for ultrasonic wave velocities along different propagation directions for Chinese fir wood determined at four equilibrium MCs. The results indicated that at each specific MC, clear differences among longitudinal wave velocities V i along the three principal directions were found; the rank order was V L > V R > V T. This is a consequence of the characteristic mechanical and acoustical orthotropic anisotropy of wood (Bucur 2006; Keunecke et al. 2007). From the mechanical perspective, the sound velocities are highly correlated with material elasticity because the propagation of the sound waves generates mechanical oscillations. From the acoustical point of view, the softwood structure is like a system of closed tubes, which are oriented both in the vertical and horizontal direction. In the longitudinal direction, tracheids of Chinese fir wood are vertical tubes with a mean length-to-diameter aspect ratio of 119:1, providing high acoustical constancy. In the radial direction, ray cells are horizontal tubes, shorter than tracheids but still suitable to transmit acoustical waves. In the tangential direction, there is no continuous structure to facilitate acoustical wave conduction, therefore, the smallest sound velocities are always found in this direction (Bucur 2006).

Table 1 Moisture-dependent ultrasound wave velocities for Chinese fir wood
Full size table

With regard to the acoustic anisotropy, the measured velocity V L was about two and five times larger than V R and V T, respectively. The ultrasound velocity anisotropy has also been reported by Keunecke et al. (2007), Gonçalves et al. (2011) and Ozyhar et al. (2013b). According to Keunecke et al. (2007), the measured velocity V L was two and three times larger than V R and V T for yew (Taxus baccata L.), while V L was two and four times higher than V R and V T for spruce [Picea abies (L.) Karst.], respectively. Gonçalves et al. (2011) revealed that the velocity V L was two and three times larger than V R and V T for three kinds of wood species including Garapeira (Apuleia leiocarpa), Cupiuba (Goupia glabra) and Sydney Blue gum (Eucalyptus saligna). Ozyhar et al. (2013b) presented results of velocity measurements along the axis for beech (Fagus sylvatica L.), which showed that V L was two and four times higher than V R and V T, respectively. It appeared that the acoustic anisotropy varies among different wood species. Each species features characteristics, such as physical properties of cell walls or geometrical structure of cells, which probably affect the transmission of ultrasonic energy. Each structural element acts independently as an elementary resonator, and the spatial distribution of these resonators differs from species to species (Bucur 2006). According to Burmester (1965) and Keunecke et al. (2007), the longer the tracheid lumens, the faster transmission of sound takes place. Moreover, the high percentage of wood rays causes an irregular grain, which could decrease the ultrasound velocity along the longitudinal direction, and lead to the relatively high ultrasound velocity in the radial direction (Niemz et al. 1999; Keunecke et al. 2007).

3.2 Influence of moisture content on ultrasound velocities

A decreasing trend of ultrasound wave velocities with wood MC was confirmed by the present investigations (Table 1). As shown in Fig. 3, for the range of MC investigated in this study, it was demonstrated that MC has a statistically significantly negative influence on ultrasound velocity using a linear regression model (at 95% level), which is also described in literature (Sakai et al. 1990; Keunecke et al. 2007; Ozyhar et al. 2013b). This is attributed to the fact that sound velocity is directly related to the presence of bound water in the wood structure (Bucur 2006). The decrease rate of ultrasound velocity with MC was obtained directly from the angular coefficient of the regression line (Fig. 3), using the parameter of DV/DMC.

Fig. 3
figure 3

Linear regression analyses of moisture content (left) or relative humidity (right) and ultrasound velocities. R = correlation coefficient; the regression model is statistically significant at P < 0.05

Full size image

Moisture-dependent orthotropic ultrasound velocities for Chinese fir wood are almost unavailable in literature. Some references covering these properties for spruce, yew and beech wood were found (Keunecke et al. 2007; Ozyhar et al. 2013b). The comparison of the calculation results obtained in this study with literature data is presented in Table 2. The decrease rate of ultrasound velocity with MC (DV/DMC) for Chinese fir wood exhibited pronounced differences to that for other wood species, irrespective of L, R or T directions. Although very small difference in the raw density was found between Chinese fir and spruce, the DVL/DMC was two times higher and DVR/DMC or DVT/DMC were nearly three times greater for Chinese fir than for spruce. Considering the wood hygroscopicity varied among species due to the different amounts of extractives (Nzokou and Kamdem 2004), the parameter of DV/DRH was used to compare the decrease rate of velocity with RH among different species. According to Fig. 3, ultrasound velocity decreased linearly with increasing RH; the DV/DRH value was obtained by the inclination of the regression line and is presented in Table 2. In regard to the decrease rate of ultrasound velocity with RH (DV/DRH), the observed differences among the species were rather small, especially between the two species with similar raw density, such as Chinese fir and spruce, yew and beech. The different performance between DV/DMC and DV/DRH may be attributed to the equilibrium moisture content varying among different species for a given RH condition, as shown in Table 2.

Table 2 Decrease rate of ultrasound velocity with MC and RH
Full size table

3.3 Moisture-dependent Young’s moduli anisotropy

3.3.1 Comparison of stiffness coefficients and Young’s moduli

Table 3 shows the moisture-dependent Young’s moduli (stiffness coefficients) in all orthotropic directions for Chinese fir obtained by means of ultrasonic method, compression and tension tests. In general, the stiffness coefficients obtained by ultrasound and the Young’s moduli determined by static methods were essentially different according to Duncan’s multiple range test. Compared with the compression or tension Young’s moduli, significantly higher values were found for the ultrasonic stiffness coefficients in all the three anatomical directions. As for “ultrasonic” vs. “compression”, the former showed a higher value than the latter with 15.7–22.1% in L, 69.1–74.6% in R, and 30.0–45.5% in T; with regard to “ultrasonic” vs. “tension”, the former also showed a higher value than the latter with 1.9–6.2% in L, 68.1–73.0% in R, and 25.0–36.4% in T over the measured MC range. The results confirmed that when stiffness coefficients for wood obtained by the ultrasonic technique without taking the non-diagonal terms of the stiffness matrix into account (Eq. 2), tend to deliver higher values than Young’s moduli values obtained in static tests (Oliveira et al. 2002; Bucur 2006; Keunecke et al. 2007; Gonçalves et al. 2011, 2014). This general trend was in agreement with the higher ultrasonic stiffness coefficients obtained in this study.

Table 3 Moisture-dependent Young’s moduli stiffness coefficients of Chinese fir wood determined by ultrasound, compression and tension methods
Full size table

There were differences in Young’s moduli (stiffness coefficients) among the three grain orientations, for both ultrasound method and static test; the value obtained in L was much higher than those in R and T (Table 3). Tracheids orientation in the longitudinal direction contributes to the high E L or C LL. As for the values obtained by ultrasonic test, C RR was about three times higher than C TT. While the values obtained by static tests indicated that E R was only slightly higher than E T, this is probably as the “dog-bone” shaped samples prepared for testing the compression and tension properties in the R direction were shown to be weak in the wide earlywood area, leading to the low Young’s moduli in R direction. However, the use of small cubes (10, 13 and 16 mm) for ultrasonic tests could minimize the influence of the curvature of growth rings, and showed more reasonable C RR value compared with the E R value obtained by above mentioned static tests using “dog-bone” shaped samples. The explanation for the difference in elastic properties between the radial and tangential directions, however, was sometimes controversial. Some researchers stated that the radial direction with alternating earlywood and latewood cellular structures has a higher modulus because the ray cells in the radial directions are acting as stiffening ribs (Jernqvist and Thuvander 2001). Some researchers believed that the transverse anisotropy is the result of pits in the radial cell wall. The cellulose microfibrils are distorted by pits in the longitudinal direction giving the radial cell wall higher transverse stiffness (Mark 1967). The irregular polygonal cell structure in softwood has higher stiffness in the radial direction (Astley et al. 1998; Watanabe 1998; Kifetew 1999). Other researchers proposed that the latewood could be considered as stiff ribs, which are already buckled at a small angle with very soft earlywood lying between the ribs, making the tangential modulus lower (Backman and Lindberg 2001).

Table 3 clearly indicates a decreasing trend with increasing MC in all orthotropic directions for all ultrasonic, compression and tension values. The graphical illustration of the measured elastic parameters reveals a nearly linear relationship with the MC (Fig. 4). While the Young’s moduli (stiffness coefficients) were shown to decrease with increasing MC, the individual values obtained in the three main anatomy directions were affected by the MC to a different degree. With a decrease of 24.7–29.5% in L, 34.1–45.5% in R, and 32.7–45.5% in T over the measured MC range, the decline in the R and T directions was more pronounced than that in the L direction. A similar trend was reported by Hering et al. (2012) and Ozyhar et al. (2012). They showed that, in general, the E L for European beech wood is less sensitive to MC changes than the moduli in the directions perpendicular to the grain. While for Douglas fir (Pseudotsuga menziesii), the perpendicular to the grain moduli change with MC at 8–10 times the rate for the E L (McBurney and Drow 1962). Though the values were clearly higher than the relationship published in this study, the results presented here confirmed that E R (C RR) and E T (C TT) were affected by the MC to a higher degree than the E L (C LL).

Fig. 4
figure 4

Moisture-dependent Young’s moduli E (stiffness coefficients C) for Chinese fir wood determined by ultrasonic test with and without correction, compression and tension. Note: the stiffness coefficients C LL, C RR and C TT were determined by ultrasonic test. The Young’s moduli E L, E R and E T were obtained by ultrasonic-corrected C, ultrasonic-corrected T, compression and tension

Full size image

To clarify the elastic anisotropy of Chinese fir wood, Table 3 summarizes the elastic ratios obtained for the four specific MC using the ultrasonic, compression and tension methods. According to Bodig and Jayne (1982), the relationships between the longitudinal and transverse elasticity moduli vary greatly among species, but overall, the magnitudes of Young’s moduli ratios are approximately E L:E R:E T ≈ 20:1.6:1.0. It was noted that in this study, the C LL/C TT ratios determined by ultrasonic technique or E L/E T ratios obtained by static tests at lower MC (10.3 and 12.2%) were similar to values suggested by Bodig and Jayne (1982), but it showed large E L/E T ratios obtained by static tests at higher MC (14.6 and 16.7%). This result suggested that the orthotropy of Chinese fir wood in the present study is similar to that expected by Bodig and Jayne (1982), who reported that an E L/E T ratio near 24:1 would make the wood the most highly orthotropic material known to man. Tracheids orientation in the longitudinal direction gives the higher longitudinal stiffness, and in the case of radial and tangential stiffness, the smaller the density, the lower these values will be (Keunecke et al. 2007; Gonçalves et al. 2011). Consequently, lower density species such as Chinese fir wood tend to produce smaller radial and tangential stiffness and, therefore, larger differences between Young’s moduli in longitudinal and transverse directions. In the case of E R/E T, the present static tests results were also similar to the values suggested by Bodig and Jayne (1982), while the C RR/C TT values obtained by ultrasonic tests were about three times higher than the E R/E T determined by static tests. Furthermore, there was no statistically significant correlation between stiffness coefficients ratios and MC in ultrasonic tests (Fig. 5). This finding was in consistence with findings in previous studies (Ozyhar et al. 2012, 2013b), where no evidence of the influence of the MC on the elastic anisotropy for European beech wood measured by ultrasound method could be found. While some Young’s moduli ratios exhibited increasing trend with the increase of MC in compression or tension tests.

Fig. 5
figure 5

Linear regression analyses of elastic ratios and MC. R = correlation coefficient; the regression model is statistically significant at P < 0.05

Full size image

3.3.2 Stiffness coefficients corrected by Poisson ratio

As mentioned earlier, the overestimation of the stiffness coefficients is a consequence of the use of a simplified equation (Eq. 2). To estimate the extent of the error, the effect of a correction with the Poisson ratio was investigated on the dataset for Chinese fir obtained by Epoch. As the Poisson ratios were determined by compression and tension tests in previous work (Table 4), the values in Table 4 were used for the calculation of correction factors K (Table 5). Different Poisson’s ratio values in compression and tension (Table 4) indicated that the loading direction (compression, tension) appears to have a great influence on the Poisson’s ratio values. This is in accordance with the finding published in Ozyhar et al. (2013a), where an evidence of the influence of loading direction (compression, tension) on wood’s Poisson’s ratios could be found. A correction (Eq. 6) of the data based on the Poisson ratio was used according to Bucur (2006):

Table 4 Moisture-dependent compressive and tensile Poisson ratios of Chinese fir wood
Full size table
Table 5 Correction factors (K) calculated at different MC for ultrasonic Young’s moduli determined by compressive and tensile Poisson ratios of Chinese fir wood
Full size table
$$\begin{gathered} E_{{Lc}} = C_{{LL}} \times k_{L} \left( {\nu _{{ij}} } \right) = \rho V_{L}^{2} \frac{{1 - v_{{LR}} \times v_{{RL}} - v_{{RT}} \times v_{{TR}} - v_{{LT}} \times v_{{TL}} - v_{{LR}} \times v_{{RT}} \times v_{{TL}} - v_{{RL}} \times v_{{LT}} \times v_{{TR}} }}{{1 - v_{{RT}} \times v_{{TR}} }} \hfill \\ E_{{Rc}} = C_{{RR}} \times k_{R} \left( {\nu _{{ij}} } \right) = \rho V_{R}^{2} \frac{{1 - v_{{LR}} \times v_{{RL}} - v_{{RT}} \times v_{{TR}} - v_{{LT}} \times v_{{TL}} - v_{{LR}} \times v_{{RT}} \times v_{{TL}} - v_{{RL}} \times v_{{LT}} \times v_{{TR}} }}{{1 - v_{{LT}} \times v_{{TL}} }} \hfill \\ E_{{Tc}} = C_{{TT}} \times k_{T} \left( {\nu _{{ij}} } \right) = \rho V_{T}^{2} \frac{{1 - v_{{LR}} \times v_{{RL}} - v_{{RT}} \times v_{{TR}} - v_{{LT}} \times v_{{TL}} - v_{{LR}} \times v_{{RT}} \times v_{{TL}} - v_{{RL}} \times v_{{LT}} \times v_{{TR}} }}{{1 - v_{{LR}} \times v_{{RL}} }} \hfill \\ \end{gathered}$$
(6)

where E ic is ultrasonic Young’s moduli corrected by Poisson ratio, C ii is stiffness coefficient calculated by Eq. (2), K i is correction factor calculated by Poisson ratio, \({v_{ij}}\) is Poisson ratio determined by compression or tension.

From Table 3, comparing the elastic values between the “ultrasonic” and “ultrasonic-corrected C” or “ultrasonic-corrected T”, it was found that the stiffness coefficients corrected by the Poisson ratio led to lower values. On the other hand, comparing the Young’s moduli values between “ultrasonic-corrected C” and “compression” or between “ultrasonic-corrected T” and “tension”, respectively, it was revealed that the stiffness coefficients values corrected by Poisson ratio were higher or lower than the Young’s moduli determined by static tests. The differences between stiffness coefficients and Young’s moduli were significantly reduced by corrections with Poisson ratio in the three main anatomy directions: for “ultrasonic-corrected C” vs. “compression”, the difference of 0.2–7.1% in L, 56.1–63.6% in R, and 3.7–21.7% in T; as for “ultrasonic-corrected T” vs. “tension”, the difference of 7.0–11.7% in L, 49.2–59.0% in R, and 5.0–15.4% in T over the measured MC range. The results also indicated that the stiffness coefficients corrected by the Poisson ratio were statistically equivalent to those obtained statically in tangential direction. In the case of longitudinal and radial directions, significant differences were still found between the values obtained by ultrasound with Poisson ratio correction and obtained with static compression and tension. These results are similar to the findings published in Ozyhar et al. (2013b), where the ultrasonic Young’s moduli calculated through the complete stiffness matrix in the radial and tangential direction were in good agreement with the Young’s moduli obtained by static test, though the ultrasonic longitudinal Young’s moduli showed significant difference compared with the static ones.

The moisture dependence of ultrasonic stiffness coefficients with Poisson ratio correction is presented in Fig. 4. Similar to the ultrasonic, compression and tension values, a decreasing trend with increasing MC in all orthotropic directions for both “ultrasonic-corrected C” and “ultrasonic-corrected T” Young’s moduli were found. It was clearly exhibited that after the stiffness coefficients had been corrected by Poisson ratio, the differences between the Young’s moduli determined by ultrasonic and static tests were reduced, especially in radial and tangential directions. Furthermore, the stiffness coefficients obtained by ultrasound with Poisson ratio correction and Young’s moduli values determined by static tests were statistically equivalent in tangential direction. The results obtained in this study were in agreement with the general trend presented by Gonçalves et al. (2011), who indicated that when the stiffness constants were corrected by the Poisson ratio, the elastic parameters obtained by ultrasound showed values only slightly higher than those obtained by static tests. One should notice that the use of the simplified equation (Eq. 2) should be avoided when applying the ultrasonic technique for determining material parameters and the correction with Poisson ratio is a necessary procedure (Kránitz et al. 2014). With regards to the correction factors K calculated at different MC shown in Table 5, there was no statistically significant correlation between the moisture content and correction factors K in all three directions for compression and tension tests.

The wood elastic anisotropy, reflected by Young’s moduli ratios (E L/E T, E L/E R and E R/E T) for ultrasonic Young’s moduli corrected with the Poisson ratio, are also listed in Table 3. Duncan’s multiple range test showed that the E L/E T and E L/E R ratios determined by ultrasonic technique with correction were generally significantly different to values obtained by static tests at all specific MC levels. However, in the case of E R/E T (C RR/C TT) ratios, the values obtained by means of ultrasound with and without correction were statistically equivalent, but also exhibited significant difference to the values determined by static compression or tension.

4 Conclusion

The results conformed to the expectations: the stiffness coefficients obtained by ultrasound and the Young’s moduli obtained by compression and tension were influenced by the MC and showed a decreasing trend with the increase in MC, while the elastic anisotropy, represented by elastic ratios, does not show a uniform trend with MC. The present study confirmed that the stiffness coefficients obtained by ultrasound without taking the non-diagonal terms of the stiffness matrix into account, presented significantly higher values than the compression or tension Young’s moduli in all the three anatomical directions. The differences between stiffness coefficients and Young’s moduli were significantly reduced by corrections with Poisson ratio. However, only in tangential direction, the Young’s moduli obtained by ultrasound with Poisson ratio correction were statistically equivalent to those obtained by compression and tension.