Abstract
In this paper, we aim at a reduced 2d-model describing the observable states of the magnetization in curved thin films. Under some technical assumptions on the geometry of the thin-film, it is well-known that the demagnetizing field behaves like the projection of the magnetization on the normal to the thin film. We remove these assumptions and show that the result holds for a broader class of surfaces; in particular, for compact surfaces. We treat both the stationary case, governed by the micromagnetic energy functional, and the time-dependent case driven by the Landau–Lifshitz–Gilbert equation.
Similar content being viewed by others
1 Introduction and physical motivations
According to the Landau–Lifshitz theory of ferromagnetism (cf. [6, 8, 9, 25, 29, 35]), the observable states of a rigid ferromagnetic body, occupying a region \({\varOmega }\subseteq {\mathbb {R}}^3\), are described by its magnetization \(M : {\varOmega }\rightarrow {\mathbb {R}}^3\), a vector field verifying the fundamental constraint of micromagnetism: there exists a material-dependent positive constant \(M_s \in {\mathbb {R}}_+\) such that \(| M | = M_s\) in \({\varOmega }\). In general, the spontaneous magnetization \(M_s {:=}M_s (T)\) depends on the temperature T and vanishes above a critical value \(T_c\), characteristic of each crystal type, known as the Curie temperature. Assuming the specimen at a fixed temperature well below \(T_c\), the value of \(M_s\) can be considered constant in \({\varOmega }\). Therefore, the magnetization can be expressed in the form \(M {:=}M_s {m}\) where \({m}: {\varOmega }\rightarrow {\mathbb {S}}^2\) is a vector field taking values in the unit sphere \({\mathbb {S}}^2\) of \({\mathbb {R}}^3\).
Although the modulus of \({m}\) is constant in space, in general, it is not the case for its direction. For single crystal ferromagnets (cf. [1, 3]), the observable magnetization states correspond to the local minimizers of the micromagnetic energy functional which, after a suitable normalization, reads as (cf. [35, p. 22] or [25, p. 138])
with \({m}\in H^1( {\varOmega }, {\mathbb {S}}^2)\) and \({m}\chi _{{\varOmega }}\) the extension of \({m}\) by zero outside \({\varOmega }\).
The variational problem (1) is non-convex, non-local, and contains multiple length scales.
The first term, \({{\mathcal {E}}} \left( {m}\right) \), is the exchange energy and penalizes nonuniformities in the orientation of the magnetization. It summarizes the effects of short-range exchange interactions among neighbor spins. The magnetocrystalline anisotropy energy, \({\mathcal {A}} \left( {m}\right) \), models the existence of preferred directions of the magnetization; the energy density \(\varphi _{{\text {an}}}:{\mathbb {S}}^2 \rightarrow {\mathbb {R}}_+\) is a nonnegative function that vanishes only on a finite set of directions, the so-called easy axes. The quantity \({{\mathcal {W}}} \left( {m}\right) \) represents the magnetostatic self-energy and describes the energy due to the demagnetizing field (stray field) \({\varvec{h}_{\textsf {d}}}[ {m}\chi _{{\varOmega }}]\) generated by \({m}\chi _{{\varOmega }} \in L^2( {\mathbb {R}}^3, {\mathbb {R}}^3)\). The operator \({\varvec{h}_{\textsf {d}}}: {m}\mapsto {\varvec{h}_{\textsf {d}}}[{m}]\) is, for every \({m}\in L^2 ({\mathbb {R}}^3, {\mathbb {R}}^3)\), the unique solution in \(L^2 ({\mathbb {R}}^3, {\mathbb {R}}^3)\) of the Maxwell–Ampère equations of magnetostatics [9, 16, 27, 34]:
where \(\varvec{b}[{m}]\) denotes the magnetic flux density and \(\mu _0\) is the magnetic permeability of the vacuum. Finally, the term \({\mathcal {Z}} \left( {m}\right) \) is the Zeeman energy and models the tendency of the specimen to have its magnetization aligned with the (externally) applied field \(\varvec{h}_a\). The applied field is assumed to be unaffected by variations of \({m}\).
The dynamics of the magnetization is described by the Landau–Lifshitz–Gilbert (LLG) equation [20, 29]
The LLG equation is driven by the effective field \({\varvec{h}_{\textsf {eff}}}[{m}] {:=}- \partial _{{m}} {\mathcal {G}}_{{\varOmega }} \left( {m}\right) \) and includes both conservative precessional and dissipative contributions; the constant \(\alpha \) is the Gilbert damping constant.
The four terms in the energy functional (1) take into account effects originating from different spatial scales, such as short-range exchange forces and long-range magnetostatic interactions. The competition among the four contributions in (1) explains most of the striking pictures of the magnetization observable in ferromagnetic materials [25]; in particular, the domain structure already suggested in 1906 by Weiss [43], i.e., regions of uniform or slowly varying magnetization (magnetic domains) separated by thin transition layers (domain walls). Depending on the relations among the material and geometric parameters of the ferromagnetic particle, various asymptotic regimes arise, and their investigation can be efficiently carried out by the dimension reduction techniques of calculus of variations (see, e.g., [4, 12,13,14, 22, 26, 28, 37]).
1.1 State of the art
In the last decade, magnetic systems with the shape of a curved thin film have been subject to extensive experimental and theoretical research (nanotubes [23, 30], 3d helices [31, 40], thin spherical shells [17, 32, 36, 39]). The embedding of two-dimensional structures in the three-dimensional space permits to alter the magnetic properties of the system by tailoring its local curvature. Even in the case of an anisotropic crystal, curved geometries can induce an effective antisymmetric interaction and, therefore, the formation of magnetic skyrmions or other topological defects. In addition to fundamental reasons, the wide range of magnetic properties emerging in this way makes these structures well-suited for technological applications, e.g., racetrack memory devices, spin-wave filters, and magneto-encephalography (see the topical review [41]).
Under technical (and strong) assumptions on the geometry of the thin-film, it is well-known that the demagnetizing field behaves like the projection of the magnetization on the normal to the thin film. The first mathematical justification of this observation in micromagnetics emerged from the work of Gioia and James [22]; they showed that in planar thin films the effect of the demagnetizing field operator is represented by an easy-surface anisotropy term. A generalization of this result to the case of curved thin films is given in [10], although under the technical assumption that the thin geometry is generated by a surface diffeomorphic to the closed unit disk of \({\mathbb {R}}^2\). Also, in [38], a \(\varGamma \)-convergence analysis is performed on pillow-like shells, i.e., on shells of small thickness \(\varepsilon > 0\) having the form \(\varOmega _{\varepsilon } {:=}\left\{ (x, z) \in \omega \times {\mathbb {R}}: \varepsilon \gamma _1 (x) \leqslant z \leqslant \varepsilon \gamma _2 (x) \right\} \) with \(\omega \subseteq {\mathbb {R}}^2\) and \(\gamma _1, \gamma _2\) functions vanishing on the boundary of \(\omega \). All these investigations, having a local character, do not cover significant scenarios like the one of a spherical thin film [17, 36, 39]. Lack of mathematical models in this context motivated our work [15], which addressed the question but under a convexity assumption on the surface generating the thin film.
Finally, in [16] we established three distinct variational principles for the magnetostatic self-energy that, through the explicit construction of suitable families of scalar and vector potential, permit to circumvent the technical difficulties in [10, 15], at least in the stationary case. Indeed, it is essential to remark that the approach in [16], dealing with energy estimates rather than with the weak and strong convergence of the family of demagnetizing field operators (as we do in Lemma 1), is not suitable for the analysis of the time-dependent case.
1.2 Contributions of present work
The main aim of this paper is to overcome the technical assumptions on the geometry of the thin-film required in [10, 15]. We extend the validity of the reduced 2d models in [10] to the general framework of smooth (\(C^2\) is sufficient) and bounded orientable surfaces in \({\mathbb {R}}^3\). (In particular, our results cover the class of compact surfaces.) We consider both the stationary case, which is governed by the micromagnetic energy functional, and the time-dependent case driven by the Landau–Lifshitz–Gilbert equation (the methods in [16] cannot treat this case).
Note that, the extension to surfaces that do not admit (like in [10]) a single chart atlas, is not achieved by a local-to-global gluing argument. In fact, the presence of the non-local demagnetizing field operator \({\varvec{h}_{\textsf {d}}}\) (cf. (2)) makes this approach problematic. To have a rigorously justified micromagnetic model of curved thin films, the asymptotic analysis must take into account the global geometry of the surface from the very beginning; this requires some work. In that respect, our primary tool is Lemma 1 which concerns the weak limit of a family of demagnetizing field operators defined on curved thin films; we put some effort to make the proof of Lemma 1 short and direct, so that the central geometric scaling involved should appear evident (cf. Fig. 1).
We want to emphasize that, although the results in themselves are not surprising, they give a definitive answer to the long-standing question of whether the Gioia–James regime still hold for surfaces that, like the sphere, cannot be covered by a single chart. Our results give an affirmative answer to this question and, therefore, put on solid ground the 2d models currently used for the analysis and simulation of magnetism in curved geometries. Indeed, it is important to stress that although several geometric regimes can be investigated (see, e.g., the survey article [26]), the Gioia–James regime is the most interesting one for the study of magnetic skyrmions in curved geometries [41]. In this regard, the primary motivation for our paper comes from the physics community; as remarked in [19]: “being aware that these (dimension reduction) results were obtained for plane films, we assume that the same arguments are valid for smoothly curved shells”.
1.3 Outline
The paper is organized as follows. In Sect. 2, we state the main results: Lemma 1 which concerns the limiting behavior of the demagnetizing field in curved thin films; Theorem 1, which deals with the curved thin-film limit in the stationary case; and Theorem 2 that accounts for the time-dependent setting. The proof of Theorem 1 is given in Sect. 3; the analysis of the limiting LLG equation is in Sect. 4.
2 Statement of main results
In the following, S will always denote a bounded, orientable, and smooth (\(C^2\)) surface in \({\mathbb {R}}^3\). The normal field associated with the choice of orientation for S will be denoted by \(n: S \rightarrow {\mathbb {S}}^2\). We stress that although in the following we will always refer to surfaces without boundary, the distinction between surfaces with or without boundary is here irrelevant; indeed, contributions due to the presence of a boundary can appear only at higher-order terms in the expansion of the demagnetizing field.
2.1 Notation and setup
For every \(\xi \in S\) and every \(\delta \in {\mathbb {R}}^{}\) we denote by \(\ell _{\delta } (\xi ) {:=}\left\{ \xi + {s}n(\xi ) \right\} _{\left| {s}\right| < \delta }\) the normal segment to S having radius \(\delta \) and centered at \(\xi \). We say that S admits a tubular neighborhood (of uniform thickness) if there exists a \(\delta \in {\mathbb {R}}_+\) such that the following properties hold (cf. [18, p. 112]):
-
(1)
For every \(\xi _1, \xi _2 \in S\) one has \(\ell _{\delta } (\xi _1) \cap \ell _{\delta } (\xi _2) = \emptyset \) whenever \(\xi _1 \ne \xi _2\), and the union \({\varOmega }_{\delta } {:=}\cup _{\xi \in S} \ell _{\delta } (\xi )\) is an open set of \({\mathbb {R}}^3\) containing S.
-
(2)
Set \({{\mathcal {M}}} {:=}S \times I\), \(I {:=}(- 1, 1)\). For every \(0< \varepsilon < \delta \), the map
$$\begin{aligned} \psi _{\varepsilon } : \left( \xi , {s}\right) \in {{\mathcal {M}}} \mapsto \xi + \varepsilon {s}n(\xi ) \in {\varOmega }_{\varepsilon } \end{aligned}$$(4)is a \(C^1\)-diffeomorphism of \({{\mathcal {M}}}\) onto \({\varOmega }_{\varepsilon }\). In particular, the nearest point projection
$$\begin{aligned} \pi : {\varOmega }_{\varepsilon } \rightarrow S, \end{aligned}$$(5)which maps any \(x \in {\varOmega }_{\varepsilon }\) onto the unique \(\xi \in S\) such that \(x \in \ell _{\varepsilon } (\xi )\), is a smooth (\(C^1\)) map.
The open set \({\varOmega }_{\delta }\) is then called a tubular neighborhood of S of thickness \(\delta \). Note that
In what follows, to shorten notation, for any \(\delta > 0\) we will set \(I_{\delta } {:=}(- \delta , \delta )\) and \(I_{\delta ^+} {:=}(0, \delta )\).
Remark 2.1
The range of surfaces included by our analysis is broad. Indeed, any compact and smooth surface is orientable and admits a tubular neighborhood (of uniform thickness) [18, Prop. 1, p. 113]. In particular, our analysis holds for bounded convex surface (e.g., planar surfaces, the sphere, the ellipsoid) as well as non-convex ones (e.g., the torus). Also, it covers the class of bounded surfaces that are diffeomorphic to an open subset of a compact surface (e.g., the finite cylinder or the graph of a \(C^2\) function).
For every \(\xi \in S\) the symbols \(\tau _1 (\xi ), \tau _2 (\xi )\) are used to denote an orthonormal basis of \(T_{\xi } S\) made by its principal directions, i.e., an orthonormal basis consisting of eigenvectors of the shape operator of S (cf. [18, p. 146]). We then write \(\kappa _1 (\xi ), \kappa _2 (\xi )\) for the principal curvatures at \(\xi \in S\). Note that, for any \(x \in {\varOmega }_{\delta }\) the trihedron
constitutes an orthonormal basis of \(T_{\pi (x)} {\varOmega }_{\delta }\) that depends only on S. Also, we denote by \(\sqrt{{{\mathfrak {g}}}_{\varepsilon }}\) the metric factor which relates the volume form on \({\varOmega }_{\varepsilon }\) to the volume form on \({{\mathcal {M}}}\), by \({\mathfrak {h}}_{1, \varepsilon }, {\mathfrak {h}}_{2, \varepsilon }\) the metric coefficients which link the gradient on \({\varOmega }_{\varepsilon }\) to the gradient on \({{\mathcal {M}}}\). A direct computation shows that (cf., e.g., [33, p. 69])
where \(H (\xi )\) and \(G (\xi )\) are, respectively, the mean and Gaussian curvature at \(\xi \in S\). In what follows, we shall always assume that the thickness \(\delta \) is sufficiently small so that
for some positive constant \(c_{{{\mathcal {M}}}}\), and every \(\varepsilon \in I_{\delta ^+}\).
Also, we shall denote by \(H^1 \left( {{\mathcal {M}}}, {\mathbb {R}}^3 \right) \) the Sobolev space of vector-valued functions defined on \({{\mathcal {M}}}\) (see [2]) endowed with the norm
Here, \({\nabla _{ \xi \,}}u\) is the tangential gradient of u on S. Finally, we write \(H^1( {{\mathcal {M}}}, {\mathbb {S}}^2)\) for the subset of \(H^1( {{\mathcal {M}}}, {\mathbb {R}}^3)\) made by vector-valued functions with values in \({\mathbb {S}}^2\).
Next, we recall that (cf. [16]), if \({\varOmega }\) is a bounded domain, \({m}\in L^2( {\varOmega }, {\mathbb {R}}^3)\), and \({\varvec{h}_{\textsf {d}}}[ {m}\chi _{{\varOmega }}] \in L^2( {\mathbb {R}}^3, {\mathbb {R}}^3)\) is a solution of the Maxwell–Ampère equations (2) then, by Poincaré’s lemma, \({\varvec{h}_{\textsf {d}}}[ {m}\chi _{{\varOmega }}] = \nabla v_{{m}}\) where \(v_m\) is the unique solution in \(H^1 \left( {\mathbb {R}}^3 \right) \) of the Poisson’s equation
Therefore, the demagnetizing field can be described as the map which to every magnetization \({m}\in L^2( {\mathbb {R}}^3, {\mathbb {R}}^3)\) associates the distributional gradient of the unique solution of (11) in \(H^1({\mathbb {R}}^3)\). It is easily seen that the map \(- {\varvec{h}_{\textsf {d}}}: {m}\in L^2 ( {\varOmega }, {\mathbb {R}}^3 ) \mapsto - \nabla v_{{m}} \in L^2( {\mathbb {R}}^3, {\mathbb {R}}^3)\) defines a self-adjoint and positive-definite bounded linear operator from \(L^2( {\mathbb {R}}^3, {\mathbb {R}}^3)\) into itself:
for every \({m}\in L^2( {\varOmega }, {\mathbb {R}}^3)\). Moreover, for any \(\varepsilon \in I_{\delta ^+}\), the demagnetizing field \({\varvec{h}_{\textsf {d}}}[ {m}\chi _{{\varOmega }_{\varepsilon }}]\) satisfies the weak form of the Maxwell–Ampère equations (cf. [16])
for every \(\varphi \in H^1 \left( {\mathbb {R}}^3 \right) \) and every \(\varvec{\varphi } \in H^1 \left( {\mathbb {R}}^3, {\mathbb {R}}^3 \right) \).
The anisotropy energy density \(\varphi _{{\text {an}}} : {\mathbb {S}}^2 \rightarrow {\mathbb {R}}_+\), which does not depend on \(\varepsilon \in I_{\delta ^+}\), is assumed to be a nonnegative Lipschitz continuous function that vanishes only along the easy directions. The hypotheses on \(\varphi _{{\text {an}}}\) are sufficiently general to embrace all classes of crystal anisotropies arising in applications (e.g., uniaxial, triaxial, and cubic, where the anisotropy density is a polynomial on \({\mathbb {S}}^2\)). Finally, the applied field \(\varvec{h}_a\) is assumed to be Lipschitz continuous.
The crucial tool for our dimension reduction analysis, both in the stationary and time-dependent case, is contained in the next result, whose proof will be given in Sect. 3.5.
Lemma 1
Let \((u_{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\) be a family in \(L^2 \left( {{\mathcal {M}}}, {\mathbb {R}}^3 \right) \) such that \(u_{\varepsilon } \left( \xi , {s}\right) \rightharpoonup u_0 (\xi ) \chi _I \left( {s}\right) \) weakly in \(L^2 ( {{\mathcal {M}}}, {\mathbb {R}}^3 )\), with \(u_0 \in L^2 (S)\). Then, with \(I_{\delta / \varepsilon } {:=}(- \delta / \varepsilon , \delta / \varepsilon )\) , there holds
Here, the symbol \(\varvec{h}_{\varepsilon } [u_{\varepsilon }] \in L^2 ( {{\mathcal {M}}}, {\mathbb {R}}^3)\) stands for the demagnetizing field on \({{\mathcal {M}}}\) defined by (cf. (21)):
and the family of diffeomorphisms \((\psi _{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\) is the one given in (4).
Moreover, if \(u_{\varepsilon } \left( \xi , {s}\right) \rightarrow u_0 (\xi ) \chi _I \left( {s}\right) \) strongly in \(L^2( {{\mathcal {M}}}, {\mathbb {R}}^3 )\), then the convergence in (15) is strong in \(L^2( S \times {\mathbb {R}}, {\mathbb {R}}^3)\).
Remark 2.2
Note that, in particular, we have that \(\varvec{h}_{\varepsilon } [u_{\varepsilon }] \rightharpoonup - \left( u_0 (\xi ) \cdot n(\xi ) \right) n (\xi )\) weakly in \(L^2( {{\mathcal {M}}}, {\mathbb {R}}^3)\) if \(u_{\varepsilon } \left( \xi , {s}\right) \rightharpoonup u_0 (\xi ) \chi _I \left( {s}\right) \) weakly in \(L^2( {{\mathcal {M}}}, {\mathbb {R}}^3 )\). Also, \(\varvec{h}_{\varepsilon } [u_{\varepsilon }] \rightarrow - \left( u_0 (\xi ) \cdot n(\xi ) \right) n (\xi )\) strongly in \(L^2( {{\mathcal {M}}}, {\mathbb {R}}^3)\) if \(u_{\varepsilon } \left( \xi , {s}\right) \rightarrow u_0 (\xi ) \chi _I \left( {s}\right) \) strongly in \(L^2 ( {{\mathcal {M}}}, {\mathbb {R}}^3 )\).
2.2 The stationary case: the micromagnetic energy functional on curved thin films
To avoid uninformative results (i.e., to avoid that the \(\varGamma \)-limit reduces to the null functional), we consider a rescaled version of the energy functional (1). Precisely, let \({\varOmega }_{\delta }\) be a bounded open set generated as a tubular neighborhood of a smooth orientable surface S. For any \(\varepsilon \in I_{\delta ^+} {:=}(0, \delta )\) we denote by \({\mathcal {G}}_{\varepsilon }\) the micromagnetic energy functional defined on \(H^1( {\varOmega }_{\varepsilon }, {\mathbb {S}}^2)\) by
where \({m}\chi _{{\varOmega }_{\varepsilon }}\) is the extension by zero of \({m}\) to the whole space outside \({\varOmega }_{\varepsilon }\). The existence for any \(\varepsilon \in I_{\delta ^+}\) of at least a minimizer for \({\mathcal {G}}_{\varepsilon }\) in \(H^1( {\varOmega }_{\varepsilon }, {\mathbb {S}}^2)\) is a straightforward application of the direct method of the calculus of variations (cf. [42]).
We are interested in the asymptotic behavior of the family of minimizers of \(({\mathcal {G}}_{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\) as \(\varepsilon \rightarrow 0\).
Let us introduce the following functionals defined on \(H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2)\), which can be thought as the pull-back of \({{\mathcal {E}}}_{\varepsilon }, {{\mathcal {W}}}_{\varepsilon }, {\mathcal {A}}_{\varepsilon }\) and \({\mathcal {Z}}_{\varepsilon }\) on the product manifold \({{\mathcal {M}}} {:=}S \times I\), \(I {:=}(- 1, 1)\):
-
The exchange energy on \({{\mathcal {M}}}\) reads as
$$\begin{aligned} {{\mathcal {E}}}_{{{\mathcal {M}}}}^{\varepsilon } (u)&{:=}\frac{1}{2} \int \limits _{{{\mathcal {M}}}} \sum _{i = 1}^2 \left| {\mathfrak {h}}_{i, \varepsilon } \left( \xi , {s}\right) \partial _{\tau _i (\xi )} u \left( \xi , {s}\right) \right| ^2 \sqrt{{{\mathfrak {g}}}_{\varepsilon } \left( \xi , {s}\right) } \mathrm {d}\xi \mathrm {d}{s}\nonumber \\&\quad + \frac{1}{2 \varepsilon ^2} \int \limits _{{{\mathcal {M}}}} \left| \partial _{{s}} u \left( \xi , {s}\right) \right| ^2 \sqrt{{{\mathfrak {g}}}_{\varepsilon } \left( \xi , {s}\right) } \mathrm {d}\xi \mathrm {d}{s}. \end{aligned}$$(19) -
The magnetostatic self-energy on \({{\mathcal {M}}}\) is defined by
$$\begin{aligned} {{\mathcal {W}}}_{{{\mathcal {M}}}}^{\varepsilon } (u) {:=}- \frac{1}{2} \int \limits _{{{\mathcal {M}}}} \varvec{h}_{\varepsilon } [u] \left( \xi , {s}\right) \cdot u \left( \xi , {s}\right) \sqrt{{{\mathfrak {g}}}_{\varepsilon } \left( \xi , {s}\right) } \mathrm {d}\xi \mathrm {d}{s}. \end{aligned}$$(20)Here, the symbol \(\varvec{h}_{\varepsilon } [u] \in L^2 ( {{\mathcal {M}}}, {\mathbb {R}}^3 )\) stands for the demagnetizing filed on \({{\mathcal {M}}}\):
$$\begin{aligned} \varvec{h}_{\varepsilon } [u] {:=}{\varvec{h}_{\textsf {d}}}[(u \chi _I) \circ \psi ^{- 1}_{\varepsilon }] \circ \psi _{\varepsilon } . \end{aligned}$$(21)The family of diffeomorphisms \((\psi _{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\) is the one given in (4).
-
The anisotropy and interaction energies on \({{\mathcal {M}}}\), respectively, given by
$$\begin{aligned} {\mathcal {A}}_{{{\mathcal {M}}}}^{\varepsilon } (u)&{:=}&\int \limits _{{{\mathcal {M}}}} \varphi _{{\text {an}}} ( u ( \xi , {s}) ) \sqrt{{{\mathfrak {g}}}_{\varepsilon } \left( \xi , {s}\right) } \mathrm {d}\xi \mathrm {d}{s}, \end{aligned}$$(22)$$\begin{aligned} {\mathcal {Z}}_{{{\mathcal {M}}}}^{\varepsilon } (u)&{:=}&- \int \limits _{{{\mathcal {M}}}} \varvec{h}_a^{\varepsilon } \left( \xi , {s}\right) \cdot u \left( \xi , {s}\right) \sqrt{{{\mathfrak {g}}}_{\varepsilon } \left( \xi , {s}\right) } \mathrm {d}\xi \mathrm {d}{s}. \end{aligned}$$(23)For every \(\varepsilon \in I_{\delta ^+}\), we have used the symbol \(\varvec{h}_a^{\varepsilon }\) for the expression of \(\varvec{h}_a\) on \({{\mathcal {M}}}\) which, for every \(\left( \xi , {s}\right) \in {{\mathcal {M}}}\), is defined by \(\varvec{h}_a^{\varepsilon } \left( \xi , {s}\right) {:=}\varvec{h}_a \left( \psi _{\varepsilon } \left( \xi , {s}\right) \right) \). Note that, in the new coordinate system, the applied field depends upon \(\varepsilon \in I_{\delta ^+}\).
The main result for the stationary case is stated in the next result.
Theorem 1
For any \(\varepsilon \in I_{\delta ^+}\), the minimization problem for \({\mathcal {G}}_{\varepsilon }\) in \(H^1( {\varOmega }_{\varepsilon }, {\mathbb {S}}^2)\) is equivalent to the minimization in \(H^1( {{\mathcal {M}}}, {\mathbb {S}}^2)\) of the functional \({{\mathcal {F}}}_{\varepsilon }\) defined by
By this, we mean that a configuration \({m}_{\varepsilon } \in H^1( {\varOmega }_{\varepsilon }, {\mathbb {S}}^2)\) minimizes \({\mathcal {G}}_{\varepsilon }\) if and only if \(u_{\varepsilon } {:=}{m}_{\varepsilon } \circ \psi _{\varepsilon } \in H^1( {{\mathcal {M}}}, {\mathbb {S}}^2)\) minimizes \({{\mathcal {F}}}_{\varepsilon }\).
The family \(({{\mathcal {F}}}_{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\) is equicoercive in the weak topology of \(H^1 \left( {{\mathcal {M}}}, {\mathbb {S}}^2 \right) \) and the \(\varGamma \)-limit \({{\mathcal {F}}}_0 {:=}\varGamma - \lim _{\varepsilon \rightarrow 0} {{\mathcal {F}}}_{\varepsilon }\) is given by
if \(\partial _{{s}} u \, = \,0\) and \(+ \infty \) otherwise. Therefore,
and if \((u_{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\) is a minimizing family for \(({{\mathcal {F}}}_{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\), there exists a subsequence of \((u_{\varepsilon })_{\varepsilon \in I_{\delta +}}\) which weakly converges in \(H^1( {{\mathcal {M}}}, {\mathbb {S}}^2)\) to a minimum point of \({{\mathcal {F}}}_0\).
The proof of Theorem 1 is given in several steps. In Sect. 3.1 we show that for any \(\varepsilon \in I_{\delta +}\) and any \({m}_{\varepsilon } \in H^1 \left( {\varOmega }_{\varepsilon }, {\mathbb {S}}^2 \right) \) the equality \({\mathcal {G}}_{\varepsilon } \left( {m}_{\varepsilon } \right) \, = \,{{\mathcal {F}}}_{\varepsilon } \left( {m}\circ \psi _{\varepsilon } \right) \) holds, where \(\psi _{\varepsilon }\) stands for the diffeomorphism of \({{\mathcal {M}}}\) onto \({\varOmega }_{\varepsilon }\) given by \(\psi _{\varepsilon } \left( \xi , {s}\right) {:=}\xi + \varepsilon {s}n(\xi )\). In Sect. 3.2 we show that the family \(({{\mathcal {F}}}_{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\) is equicoercive for the weak topology of \(H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2)\). Finally, the complete characterization of the \(\varGamma \)-limit \({{\mathcal {F}}}_0\) is the object of Sects. 3.3–3.5.
Remark 2.3
Note that, the families \(({\mathcal {A}}^{\varepsilon }_{{{\mathcal {M}}}})_{\varepsilon \in I_{\delta +}}\) and \(({\mathcal {Z}}^{\varepsilon }_{{{\mathcal {M}}}})_{\varepsilon \in I_{\delta +}}\) are a continuous perturbation of \(({{\mathcal {E}}}_{{{\mathcal {M}}}}^{\varepsilon } +{{\mathcal {W}}}_{{{\mathcal {M}}}}^{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\). This means that, with respect to the (topological) product space \(I_{\delta ^+} \times H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\), the following relations hold
Hence, the theorem on the sum of \(\varGamma \)-limits holds (cf. [11, Prop. 6.20, p. 62]), namely:
For this reason, in the sequel, we shall only focus on the family \(({{\mathcal {E}}}_{{{\mathcal {M}}}}^{\varepsilon } +{{\mathcal {W}}}_{{{\mathcal {M}}}}^{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\).
2.3 The time-dependent case: the Landau–Lifshitz–Gilbert equation on curved thin films
The observable states of magnetization correspond to the local minimizers of the micromagnetic energy functional (1). Hence, they are among the solutions of the Euler–Lagrange equation. If \({m}\in H^1 ( \varOmega , {\mathbb {S}}^2 )\) is a critical point of \({\mathcal {G}}_{{\varOmega }}\), then
for every \(v \in H^1 \left( {\varOmega }, {\mathbb {R}}^3 \right) \) such that \(v (x) \in T_{{m}(x)} {\mathbb {S}}^2\) for a.e. x in \({\varOmega }\). Here, \(T_{{m}(x)} {\mathbb {S}}^2\) denotes the tangent space of \({\mathbb {S}}^2\) at the point \({m}(x)\), while \(\mathrm{d}{\mathcal {G}}_{{\varOmega }} : H^1 \left( {\varOmega }, {\mathbb {R}}^3 \right) \rightarrow {\mathbb {R}}\) is the (unconstrained) Fréchet derivative of \({\mathcal {G}}_{{\varOmega }}\) at \({m}\).
In micromagnetics, \(- \mathrm{d}{\mathcal {G}}_{{\varOmega }} \left( {m}\right) \) is referred to as the effective field and usually denoted by \({\varvec{h}_{\textsf {eff}}}[{m}]\). The stationary condition (30), which in the strong form reads as
represents the so-called Brown’s static equations. In what follows, to shorten the length of the formulas, we will neglect both the magnetocrystalline anisotropy and the Zeeman energy. As already pointed out in Remark 2.3, these terms do not alter the mathematical analysis of the question. Then, a standard computation shows that for every \(\varphi \in H^1 \left( {\varOmega }, {\mathbb {R}}^3 \right) \) one has
or, in strong form, \({\varvec{h}_{\textsf {eff}}}[{m}] {:=}\Delta {m}+ {\varvec{h}_{\textsf {d}}}[ {m}]\). When the magnetization does not satisfy Brown’s static equations, the ferromagnetic system evolves in time according to the Landau–Lifshitz–Gilbert equation (LLG) [21, 29], which model the magnetization dynamics as a dissipative precessional dynamics driven by the effective field. In dimensionless form, the LLG reads as
where \(\alpha > 0\) is the Gilbert damping constant, and \(m^{*}\) is the magnetization state at time \(t = 0\).
Here, we work with the standard weak formulation, as described, e.g., in [5, 10, 24]. In what follows, for every \(T \in {\mathbb {R}}_+\) we set \({\varOmega }_T {:=}(0, T) \times {\varOmega }\).
Definition 1
Let \({\varOmega }\) be an open set of \({\mathbb {R}}^3\) and \(m^{*}\in H^1 ( {\varOmega }, {\mathbb {S}}^2 )\). We say that the vector field \({m}:{\mathbb {R}}_+\times {\varOmega }\rightarrow {\mathbb {S}}^2\) is a (global) weak solution to the LLG, if for every \(T > 0\) the following conditions are fulfilled:
-
i.
\({m}\in H^1 ( {\varOmega }_T, {\mathbb {S}}^2 ) \cap L^{\infty } ( 0, T ; H^1 ( {\varOmega }, {\mathbb {S}}^2 ) )\);
-
ii.
\({m}(0) = m^{*}\) in the trace sense;
-
iii.
For every \(\varphi \in H^1 \left( {\varOmega }_T,^{} {\mathbb {R}}^3 \right) \) there holds
$$\begin{aligned} \int \limits _0^T \left\langle {\partial _t {m}},{\varphi } \right\rangle _{{\varOmega }}&\, = \,&- \int \limits _0^T \left\langle {{\varvec{h}_{\textsf {eff}}}[{m}]},{\varphi \times {m}} \right\rangle _{{\varOmega }} + \alpha \int \limits _0^T \left\langle {\partial _t {m}},{\varphi \times {m}} \right\rangle _{{\varOmega }} . \end{aligned}$$(34) -
iv
With \({\mathcal {G}}_{{\varOmega }}\) the energy functional (1), the following energy inequality holds:
$$\begin{aligned} {\mathcal {G}}_{{\varOmega }} \left( {m}(T) \right) + \alpha \int \limits _0^T \left\| \partial _t {m}(t) \right\| _{L^2 \left( {\varOmega }, {\mathbb {R}}^3 \right) }^2 \mathrm {d}t \; \leqslant \; {\mathcal {G}}_{\varOmega } \left( m^{*}\right) . \end{aligned}$$(35)
The existence of at least a global weak solution of (33) dates back to [5]. Therefore, in our setting, for any \(\varepsilon > 0\), and any initial datum \(m^{*}_{\varepsilon } \in H^1( {\varOmega }_{\varepsilon }, {\mathbb {S}}^2)\), there exists at least a global weak solution \({m}_{\varepsilon }\) of the LLG equation on \({\varOmega }_{\varepsilon }\) with initial datum \(m^{*}_{\varepsilon }\). As in the statement of the \(\varGamma \)-convergence result, it is convenient to rewrite the LLG as an equation on the product manifold \({{\mathcal {M}}}= S \times I\). To this end, for any \({u}_{\varepsilon }\in H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\), we introduce the effective field on \({{\mathcal {M}}}\), defined for every \(\varphi \in H^1 \left( {{\mathcal {M}}}, {\mathbb {R}}^3 \right) \) by
where, to shorten notation, we set
This leads to Definition 2 below, which gives an equivalent notion of (global) weak solution for configurations evolving in time on \({{\mathcal {M}}}\). In what follows, for every \(T \in {\mathbb {R}}_+\) we set \({{\mathcal {M}}}_T {:=}(0, T) \times {{\mathcal {M}}}\). Also, with a slight abuse of notation we set
and
Definition 2
Suppose that \(u^{*}\left( \xi , {s}\right) {:=}u^{*}(\xi ) \chi _I \left( {s}\right) \) with \(u^{*}(\xi ) \in H^1 ( S, {\mathbb {S}}^2)\). We say that the vector field \({u}_{\varepsilon }: {\mathbb {R}}_+ \times {{\mathcal {M}}} \rightarrow {\mathbb {S}}^2\) is a (global) weak solution of the LLG equation if for every \(T > 0\) the following conditions are fulfilled:
-
i.
\({u}_{\varepsilon }\in H^1 ( {{\mathcal {M}}}_T, {\mathbb {S}}^2 ) \cap L^{\infty } ( 0, T ; H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2 ) )\);
-
ii.
\({u}_{\varepsilon }(0) = u^{*}\) in the trace sense;
-
iii.
For every \(\varphi \in H^1 \left( {{\mathcal {M}}}_T,^{} {\mathbb {R}}^3 \right) \) there holds
$$\begin{aligned} \int \limits _0^T \left\langle {\partial _t {u}_{\varepsilon }},{\varphi } \right\rangle _{{{\mathcal {M}}}}&\, = \,- \int \limits _0^T \left\langle {{\varvec{h}^{\varepsilon }_{\textsf {eff}}}[ {u}_{\varepsilon }]},{\varphi \times {u}_{\varepsilon }} \right\rangle _{{{\mathcal {M}}}} + \alpha \int \limits _0^T \left\langle {\partial _t {u}_{\varepsilon }},{\varphi \times {u}_{\varepsilon }} \right\rangle _{{{\mathcal {M}}}} . \end{aligned}$$(40) -
iv.
The following energy inequality holds, where \({{\mathcal {F}}}_{\varepsilon }\) represents the energy functional (24):
$$\begin{aligned} {{\mathcal {F}}}_{\varepsilon } \left( {u}_{\varepsilon }(T) \right) + \int \limits _{{{\mathcal {M}}}_T} \left| \partial _t {u}_{\varepsilon }\right| ^2 \sqrt{{{\mathfrak {g}}}_{\varepsilon }} \; \leqslant \; {{\mathcal {F}}}_{\varepsilon } \left( u^{*}\right) . \end{aligned}$$(41)
Remark 2.4
The equivalence between the two definitions has to be understood in the following sense. If \({m}_{\varepsilon }\) is a global weak solution in the sense of Definition 1 (with initial datum \(m^{*}_{\varepsilon }\)), then \({u}_{\varepsilon } (t) {:=}{m}_{\varepsilon } (t) \circ \psi _{\varepsilon }\) is a global weak solution in the sense of Definition 2 (with initial datum \(u^{*}_{\varepsilon } {:=}m^{*}\circ \psi _{\varepsilon }\)) where, as before, \(\psi _{\varepsilon } : \left( \xi , {s}\right) \in {{\mathcal {M}}} \mapsto \xi + \varepsilon {s}n(\xi ) \in {\varOmega }_{\varepsilon }\).
For curved thin films, our main result reads as follows.
Theorem 2
Let \(u^{*}\left( \xi , {s}\right) {:=}u^{*}(\xi ) \chi _I \left( {s}\right) \) with \(u^{*}(\xi ) \in H^1 \left( S, {\mathbb {S}}^2 \right) \) and, for every \(\varepsilon > 0\), let \({u}_{\varepsilon }\) be a weak solution of the LLG (in the sense of Definition 2) with initial datum \(u^{*}\). Then, there exists a vector field \({u}_0 \in L^{\infty } ( {\mathbb {R}}_+ ; H^1 ( S, {\mathbb {S}}^2 ) )\) such that, \({u}_0 \in H^1 ( S_T, {\mathbb {S}}^2)\) for every \(T > 0\) and, possibly for a subsequence, \({u}_{\varepsilon } \; \overset{*}{\rightharpoonup } {u}_0 \chi _I\) weakly\(^{*}\) in \(L^{\infty } ( {\mathbb {R}}_+ ; H^1( {{\mathcal {M}}}, {\mathbb {S}}^2 ))\) and strongly in \(L^2 ( 0, T ; L^2 ( {{\mathcal {M}}}, {\mathbb {S}}^2 ))\).
The limit vector field \({u}_0\) satisfies the LLG equation on S:
for all \(\varphi \in H^1 \left( S_T, {\mathbb {R}}^3 \right) \), with the effective field \({\varvec{h}_{\textsf {eff} }^0}\) on S given by
Moreover, \({u}_0 (0) = u^{*}\) and the following energy inequality holds for all \(T > 0\)
with \({{\mathcal {F}}}_0\) given by (26).
The proof of Theorem 2 is given in Sect. 4, and it is based on the characterization of the demagnetizing field operator on curved thin films (cf. Lemma 1).
3 The stationary case: proof of Theorem 1
3.1 The equivalence of \({\mathcal {G}}_{\varepsilon }\) and \({{\mathcal {F}}}_{\varepsilon }\)
In this section, we prove the first part of Theorem 1, namely that once introduced, for any \(\varepsilon \in I_{\delta }\), the diffeomorphism of \({{\mathcal {M}}}\) onto \({\varOmega }_{\varepsilon }\) given by \(\psi _{\varepsilon } : \left( \xi , {s}\right) \in {{\mathcal {M}}} \mapsto \xi + \varepsilon {s}n(\xi ) \in {\varOmega }_{\varepsilon }\), one has \({\mathcal {G}}_{\varepsilon } \left( {m}_{\varepsilon } \right) \, = \,{{\mathcal {F}}}_{\varepsilon } \left( {m}_{\varepsilon } \circ \psi _{\varepsilon } \right) \), and therefore \({m}_{\varepsilon }\) minimizes \({\mathcal {G}}_{\varepsilon }\) if and only if \(u_{\varepsilon } \left( \xi , {s}\right) {:=}{m}_{\varepsilon } \left( \psi _{\varepsilon } \left( \xi , {s}\right) \right) \) minimizes \({{\mathcal {F}}}_{\varepsilon }\).
We prove the equality \({{\mathcal {E}}}_{\varepsilon } \left( {m}_{\varepsilon } \right) ={{\mathcal {E}}}_{{{\mathcal {M}}}}^{\varepsilon } \left( {m}_{\varepsilon } \circ \psi _{\varepsilon } \right) \), the other ones being similar and easier. For any \({m}\in H^1 ( {\varOmega }_{\varepsilon }, {\mathbb {S}}^2)\), by coarea formula we get
In writing the last equality, we have taken into account that for any \(\left( \varepsilon , {s}\right) \in I_{\delta ^+} \times I\) the volume form on \(\psi _{\varepsilon } ({{\mathcal {M}}})\) is related to the volume form on \({{\mathcal {M}}}\) by the metric factor \(\sqrt{{{\mathfrak {g}}}_{\varepsilon } \left( \xi , {s}\right) } {:=}\left| 1 + 2 \varepsilon {s}H (\xi ) + \left( \varepsilon {s}\right) ^2 G (\xi ) \right| \). Next, we project the gradient onto the orthonormal (moving) frame \(\left( \tau _1 (\xi ), \tau _2 (\xi ), n(\xi ) \right) \) induced by S (cf. (7)). For any \(x \in {\varOmega }_{\varepsilon }\) we have \(\left| \nabla {m}_{\varepsilon } (x) \right| ^2 = \sum _{i = 1}^2 \left| \partial _{\tau _i (\xi )} {m}_{\varepsilon } (x) \right| ^2 + \left| \partial _{n(\xi )} {m}_{\varepsilon } (x) \right| ^2\) with \(\xi = \pi (x)\). Moreover, the following relations hold
from which the equality of \({{\mathcal {E}}}_{\varepsilon } \left( {m}_{\varepsilon } \right) \) and \({{\mathcal {E}}}_{{{\mathcal {M}}}}^{\varepsilon } (u_{\varepsilon })\) results. Note that the previous computation also shows that \({m}_{\varepsilon } \in H^1 ( {\varOmega }_{\varepsilon }, {\mathbb {S}}^2 )\) if and only if \({m}_{\varepsilon } \in H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\). Finally, since the superposition operator \({m}_{\varepsilon } \in H^1 ( {\varOmega }_{\varepsilon }, {\mathbb {S}}^2 ) \mapsto \left( {m}_{\varepsilon } \circ \psi _{\varepsilon } \right) \in H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2)\) is surjective, we get:
This concludes the proof of the first part of Theorem 1.
3.2 Compactness
We now show that the family \(({{\mathcal {F}}}_{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\) is equicoercive in the weak topology of \(H^1 \left( {{\mathcal {M}}}, {\mathbb {S}}^2 \right) \). This means, by definition (see [7]), that there exists a nonempty and weakly compact set \(K \subseteq H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\) such that
The equicoercivity of \(({{\mathcal {F}}}_{\varepsilon })_{\varepsilon \in I_{\delta +}}\) will assure that we can rely on the fundamental theorem of \(\varGamma \)-convergence concerning the variational convergence of minimum problems (cf. [7, 11]).
Since \({\mathcal {A}}^{\varepsilon }_{{{\mathcal {M}}}}\) and \({\mathcal {Z}}^{\varepsilon }_{{{\mathcal {M}}}}\) are uniformly bounded terms (with respect to \(\varepsilon \in I_{\delta ^+}\)), it is sufficient to show the equicoercivity of the family \({{\mathcal {V}}}_{\varepsilon } {:=}({{\mathcal {E}}}_{{{\mathcal {M}}}}^{\varepsilon } +{{\mathcal {W}}}_{{{\mathcal {M}}}}^{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\). To this end, we observe that for any constant in space \(v \in H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\) we have
Taking into account (12) and that \(\sqrt{{{\mathfrak {g}}}_{\varepsilon }}\) is bounded on \({{\mathcal {M}}}\), uniformly with respect to \(\varepsilon \in I_{\delta ^+}\), we end up with
for a suitable positive constant \(\kappa _{{{\mathcal {M}}}}\) depending only on \({{\mathcal {M}}}\). Therefore, for every \(\varepsilon \in I_{\delta ^+}\), the minimizers of \(({{\mathcal {V}}}_{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\) are in \(K ( {{\mathcal {M}}}, {\mathbb {S}}^2 ) {:=}\cup _{\varepsilon \in I_{\delta ^+}} \left\{ u \in H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2 ) : {{\mathcal {V}}}_{\varepsilon } (u) \leqslant \; \kappa _{{{\mathcal {M}}}} | {{\mathcal {M}}} | \right\} \). Also, since the principal curvatures \(\kappa _1, \kappa _2\) are bounded in S, whenever the radius \(\delta \in {\mathbb {R}}_+\) of the tubular neighborhood \({\varOmega }_{\delta }\) is sufficiently small, we have \(\inf _{\left( \xi , {s}\right) \in {{\mathcal {M}}}} {\mathfrak {h}}_{i, \varepsilon } \left( \xi , {s}\right) \geqslant c_{{{\mathcal {M}}}}\) for every \(\varepsilon \in I_{\delta ^+}\) (cf. (9)). Therefore, since \({{\mathcal {W}}}^{\varepsilon }_{{{\mathcal {M}}}}\) is always nonnegative because of (12), we get
and therefore if \(u \in K ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\) then
In other words, the set \(K ( {{\mathcal {M}}}, {\mathbb {S}}^2)\) is contained in the bounded subset \(H^1_b ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\) of \(H^1 \left( {{\mathcal {M}}}, {\mathbb {R}}^3 \right) \) given by the intersection of \(H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\) with the ball of \(H^1 \left( {{\mathcal {M}}}, {\mathbb {R}}^3 \right) \) centered at the origin and of radius \(1 + \kappa _{{{\mathcal {M}}}} / c_{{{\mathcal {M}}}}\). Thus, for any \(\varepsilon \in I_{\delta ^+}\)
To prove that \(H^1_b ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\) is weakly compact it is sufficient to show that the set \(H^1_b ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\) is weakly closed. To this end, we note that if \((u_n)_{n \in {\mathbb {N}}}\) is a sequence in \(H^1_b ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\) such that \(u_n \rightharpoonup u_0\) weakly in \(H^1 \left( {{\mathcal {M}}}, {\mathbb {R}}^3 \right) \), due to the Rellich–Kondrachov theorem, \(u_n \rightarrow u_0\) strongly in \(L^2 \left( {{\mathcal {M}}}, {\mathbb {R}}^3 \right) \), and therefore, up to the extraction of a subsequence, \(1 \equiv | u_n | \rightarrow | u_0 |\) a.e. in \({{\mathcal {M}}}\). Thus \(u_0 \left( \xi , {s}\right) \in {\mathbb {S}}^2\) for a.e. \(\left( \xi , {s}\right) \in {{\mathcal {M}}}\) and this concludes the proof.
3.3 The identification of the \(\varGamma \)-limit
In this section, we compute \({{\mathcal {F}}}_0 {:=}\varGamma - \lim _{\varepsilon \rightarrow 0} {{\mathcal {F}}}_{\varepsilon }\). As pointed out in Remark 2.3, it is sufficient to focus on the \(\varGamma \)-convergence of the family
We set \({{\mathcal {V}}}_0 {:=}{{\mathcal {E}}}_0 +{{\mathcal {W}}}_0\) with \({{\mathcal {E}}}_0\) and \({{\mathcal {W}}}_0\) given by (25). Note that, as a consequence of (12), \({{\mathcal {V}}}_{\varepsilon } (u) \geqslant 0\) for any \(u \in H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\).
Let us prove the \(\varGamma \)-\(\liminf \) inequality for \(({{\mathcal {V}}}_{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\), i.e., that for any family \((u_{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\) weakly convergent to some \(u_0 \in H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\) we have \({{\mathcal {V}}}_0 (u_0) \leqslant \liminf _{\varepsilon \rightarrow 0} {{\mathcal {V}}}_{\varepsilon } (u_{\varepsilon })\). With no loss of generality, we can assume that \(\liminf _{\varepsilon \rightarrow 0} {{\mathcal {V}}}_{\varepsilon } (u_{\varepsilon }) < + \infty \). We then have (see (19))
and taking into account (9), we find that \(\lim _{\varepsilon \rightarrow 0} \Vert \partial _t u_0 \Vert _{L^2 ({{\mathcal {M}}})} = 0\). Since \(\partial _t u_{\varepsilon } \rightharpoonup \partial _t u_0\) in \({\mathcal {D}}' ({{\mathcal {M}}})\) we infer that
Therefore, for the identification of the \(\varGamma \)-limit of \(({{\mathcal {V}}}_{\varepsilon })_{\varepsilon \in I_{\delta }}\) it is sufficient to restrict the analysis to the families of \(H^1 \left( {{\mathcal {M}}}, {\mathbb {S}}^2 \right) \) functions which weakly converge to an element \(u_0 \in H^1( {{\mathcal {M}}}, {\mathbb {S}}^2 )\) which is 0-homogeneous, i.e., of the form
for some \({\tilde{u}}_0 \in H^1 ( S, {\mathbb {S}}^2 )\), i.e., not depending on the \({s}\) variable. In the following, with a slight abuse of notation, we shall write \(u_0 (\xi )\) instead of \({\tilde{u}}_0 (\xi )\).
In computing \({{\mathcal {V}}}_0\), we first show that the \(\varGamma \)-limit of the families \(({{\mathcal {E}}}_{{{\mathcal {M}}}}^{\varepsilon })_{\varepsilon \in I_{\delta +}}\) and \(({{\mathcal {W}}}_{{{\mathcal {M}}}}^{\varepsilon })_{\varepsilon \in I_{\delta +}}\), is, respectively, equal to \({{\mathcal {E}}}_0\) and \({{\mathcal {W}}}_0\) (cf. (25)), then we prove that \({{\mathcal {V}}}_0 {:=}\varGamma - \lim _{\varepsilon \rightarrow 0} {{\mathcal {V}}}_{\varepsilon } ={{\mathcal {E}}}_0 +{{\mathcal {W}}}_0\).
3.4 The \(\varGamma \)-limit of the family \(({{\mathcal {E}}}_{{{\mathcal {M}}}}^{\varepsilon })_{\varepsilon \in I_{\delta +}}\)
This section provides the identification of the \(\varGamma \)-limit of the family of exchange energies on \({{\mathcal {M}}}\).
Proposition 1
The family \(({{\mathcal {E}}}_{{{\mathcal {M}}}}^{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\) of exchange energy on \({{\mathcal {M}}}\), \(\varGamma \)-converges, with respect to the weak topology of \(H^1( {{\mathcal {M}}}, {\mathbb {S}}^2)\), to the functional
Proof
We start by addressing the \(\varGamma \)-\(\liminf \) inequality for \(({{\mathcal {E}}}_{{{\mathcal {M}}}}^{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\). Taking into account the lower semicontinuity of the norm, for any \(u_{\varepsilon } \rightharpoonup u_0\) in \(H^1( {{\mathcal {M}}}, {\mathbb {S}}^2 )\), with \(u_0\) of the type (57), we get
In deriving the last equality, we used (56) and denoted by \({\nabla _{ \xi \,}}u_{\varepsilon } \left( \xi , {s}\right) \) the tangential gradient of \(u_{\varepsilon }\) on S whose norm, with respect to an orthonormal basis \((\tau _1 (\xi ), \tau _2 (\xi ))\) of \(T_{\xi } S\), can be expressed as \(\left| {\nabla _{ \xi \,}}u_{\varepsilon } \left( \xi , {s}\right) \right| ^2 {:=}\sum _{i = 1}^2 | \partial _{\tau _i (\xi )} u_{\varepsilon } \left( \xi , {s}\right) |^2\). Overall
Next, from (9), there exists a strictly positive real-valued function \(\gamma : I_{\delta ^+} \rightarrow {\mathbb {R}}_+\) such that, at least in a neighborhood of \(0 \in {\mathbb {R}}\), the following estimate holds:
and, therefore,
Substituting (68) into (62) we get that if \(u_{\varepsilon } \rightharpoonup u_0\) weakly in \(H^1( {{\mathcal {M}}}, {\mathbb {S}}^2)\) and \(\liminf _{\varepsilon \rightarrow 0} {{\mathcal {V}}}_{\varepsilon } (u_{\varepsilon }) < + \infty \), then the following estimate holds
We now address the existence of a recovery sequence. To this end, it is sufficient to note that for every \(u_{\varepsilon } \in H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\) having the product form \(u_{\varepsilon } \left( \xi , {s}\right) = \chi _I \left( {s}\right) u_0 (\xi )\) we have (cf. (63))
This concludes the proof. \(\square \)
3.5 Proof of Lemma 1 and the \(\varGamma \)-limit of the family \(({{\mathcal {W}}}_{{{\mathcal {M}}}}^{\varepsilon })_{\varepsilon \in I_{\delta +}}\)
This section is devoted to the identification of the \(\varGamma \)-limit of the family \(({{\mathcal {W}}}_{{{\mathcal {M}}}}^{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\) of magnetostatic self-energies on \({{\mathcal {M}}}\). We will first prove Lemma 1.
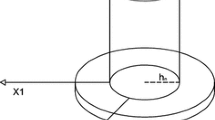
A cross section representation of the scaling procedure involved in the proof of Lemma 1
Proof of Lemma 1
We set \({m}_{\varepsilon } \chi _{{\varOmega }_{\varepsilon }} {:=}(u_{\varepsilon } \circ \psi ^{- 1}_{\varepsilon }) \chi _{{\varOmega }_{\varepsilon }}\), with \(\psi _{\varepsilon }\) given by (4); cf. Fig. 1. Recall that \({m}_{\varepsilon } \chi _{{\varOmega }_{\varepsilon }}\) denotes the extension by zero of \({m}_{\varepsilon }\) to the whole space outside \({\varOmega }_{\varepsilon }\). Note that \({m}_{\varepsilon } \chi _{{\varOmega }_{\varepsilon }}\) is in \(L^2 \left( {\mathbb {R}}^3, {\mathbb {R}}^3 \right) \) and, therefore, it is possible to evaluate the demagnetizing field \({\varvec{h}_{\textsf {d}}}\) on \({m}_{\varepsilon } \chi _{{\varOmega }_{\varepsilon }}\). Also, \({m}_{\varepsilon } \chi _{{\varOmega }_{\varepsilon }}\) is in \(L^2 ( {\varOmega }_{\delta }, {\mathbb {S}}^2 )\) and this implies that the family \((\varvec{h}_{\varepsilon } [u_{\varepsilon }] \chi _{I_{\delta / \varepsilon }})_{\varepsilon \in I_{\delta ^+}}\) is bounded in \(L^2 \left( S \times {\mathbb {R}}, {\mathbb {R}}^3 \right) \). Indeed, we have
and the last integral is bounded by a constant that does not depend on \(\varepsilon \). Therefore, since \({{\mathfrak {g}}}_{\varepsilon }\) is uniformly bounded from below in \({{\mathcal {M}}}_{\delta / \varepsilon }\) by a positive constant (cf. (9)), there exists \(\varvec{h}_{{{\mathcal {M}}}} \in L^2 \left( S \times {\mathbb {R}}, {\mathbb {R}}^3 \right) \) such that
Next, we consider the restriction of (13) and (14) to \({\varOmega }_{\delta } = \psi _{\varepsilon } ({{\mathcal {M}}}_{\delta / \varepsilon }) = \psi _{\varepsilon } (S \times I_{\delta / \varepsilon })\) where, as usual, \(\psi _{\varepsilon } : \left( \xi , {s}\right) \in {{\mathcal {M}}}_{\delta / \varepsilon } \mapsto \xi + \varepsilon {s}n(\xi ) \in {\varOmega }_{\varepsilon }\). We obtain:
Here, \(\varvec{h}_{\varepsilon } [u_{\varepsilon }]\) is the demagnetizing field on \({{\mathcal {M}}}\) defined by (16). Decomposing (75) into its normal and tangential part, we get that for any \(\varphi _{\varepsilon } \in {\mathcal {D}} ({{\mathcal {M}}}_{\delta / \varepsilon })\)
We test against functions of the type \(\varphi _{\varepsilon } (\xi , s) {:=}\varphi _S (\xi ) \cdot \varphi (s) {\text {with}} \varphi _S \in {\mathcal {D}} (S)\), \(\varphi \in {\mathcal {D}} \left( {\mathbb {R}}\right) \), and we note that for every \(\varphi \in {\mathcal {D}} \left( {\mathbb {R}}\right) \) there exists \(0< \varepsilon < \delta \) sufficiently small such that \({\text {supp}} \varphi \subseteq I_{\delta / \varepsilon }\). Therefore, for every \(\varphi \in {\mathcal {D}} \left( {\mathbb {R}}\right) \), taking into account (63) and passing to the limit for \(\varepsilon \rightarrow 0\) in (77), there holds
Thus, the function
is constant and, due to (74), in \(L^1 \left( {\mathbb {R}}\right) \); this implies that (79) is necessarily the zero function. By the arbitrariness of \(\varphi _S \in {\mathcal {D}} (S)\) we conclude that
In particular, \(\varvec{h}_{{{\mathcal {M}}}} \cdot n= 0\) in \(S \times \left( {\mathbb {R}}\backslash I \right) \).
Next, we consider the curl-free condition (76). For any \(\varphi \in {\mathcal {D}} \left( \varOmega _{\delta }, {\mathbb {R}}^3 \right) \) we set \(\varphi _{\varepsilon } {:=}\varphi \circ \psi _{\varepsilon }\). We have
Therefore, Eq. (76) reads as
As before, testing against functions of the type \(\varphi _{\varepsilon } (\xi , s) {:=}\varphi _S (\xi ) \cdot \varphi (s) {\text {with}} \varphi _S \in {\mathcal {D}} (S)\), \(\varphi \in {\mathcal {D}} \left( {\mathbb {R}}, {\mathbb {R}}^3 \right) \) and passing to the limit for \(\varepsilon \rightarrow 0\) we infer that
and by the arbitrariness of \(\varphi _S \in {\mathcal {D}} (S)\) we conclude that
Summarizing, from the previous equation and (80) we end up with
Next, suppose \(u_{\varepsilon } \left( \xi , {s}\right) \rightarrow u_0 (\xi ) \chi _I \left( {s}\right) \)strongly in \(L^2 \left( {{\mathcal {M}}}, {\mathbb {R}}^3 \right) \). We have
and by the strong convergence of \(u_{\varepsilon } \rightarrow u_0\), passing to the limit for \(\varepsilon \rightarrow 0\) in the previous relation, we obtain
The last integral coincides with the norm of \(\varvec{h}_{{{\mathcal {M}}}}\) in \(L^2 (S)\). This completes the proof. \(\square \) WAA
Coming back to the family of energy functionals \(({{\mathcal {W}}}^{\varepsilon }_{{{\mathcal {M}}}})_{\varepsilon \in I_{\delta ^+}}\), it is now simple to prove the following convergence result.
Proposition 2
If \(u_{\varepsilon } \left( \xi , {s}\right) \rightarrow u_0 (\xi ) \chi _I \left( {s}\right) \) weakly in \(H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\) for some \(u_0 \in L^2 (S)\), then
Proof
Let \((u_{\varepsilon })_{\varepsilon \in I_{\delta ^+}}\) be a family of \(H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2)\) functions weakly converging to some \(u_0 \in H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\) and such that \(\liminf _{\varepsilon \rightarrow 0} {{\mathcal {F}}}_{\varepsilon } (u_{\varepsilon }) < + \infty \). By Rellich–Kondrachov theorem, we have \(u_{\varepsilon } \rightarrow u_0\) strongly in \(L^2( {{\mathcal {M}}}, {\mathbb {R}}^3)\). By taking the limit for \(\varepsilon \rightarrow 0\) of \({{\mathcal {W}}}_{{{\mathcal {M}}}}^{\varepsilon }\) we get
The assertion follows from Lemma 1. \(\square \) WAA
3.6 The \(\varGamma \)-limit of the family \(({{\mathcal {F}}}_{\varepsilon })_{\varepsilon \in I_{\delta }}\)
We complete the proof of Theorem 1 by showing that \({{\mathcal {F}}}_0\) is given by (26). As pointed out in Remark 2.3, it is sufficient to show that \(\varGamma - \lim {{\mathcal {V}}}_{\varepsilon } \, = \,{{\mathcal {E}}}_0 +{{\mathcal {W}}}_0\). We note that if \(u_{\varepsilon } \rightharpoonup u\) in \(H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2 )\) and \(\partial _{{s}} u \ne 0\) then \(\liminf _{\varepsilon \rightarrow 0} {{\mathcal {V}}}_{\varepsilon } (u_{\varepsilon }) = + \infty \). Therefore, the \(\varGamma \)-\(\liminf \) inequality is trivially satisfied. On the other hand, if \(\partial _{{s}} u = 0\), then from Propositions 1 and 2 we get
Finally, for any \(u_0 \in H^1 ( {{\mathcal {M}}}, {\mathbb {S}}^2)\) such that \(\partial _{{s}} u_0 \, = \,0\), the constant (with respect to the index \(\varepsilon \)) family \((u_{\varepsilon })_{\varepsilon \in I_{\delta ^+}} = (u_0)_{\varepsilon \in I_{\delta ^+}}\) is a recovery sequence. This completes the proof of Theorem 1.
4 The time-dependent case: proof of Theorem 2
Let now \(\left( {u}_{\varepsilon }\right) _{\varepsilon \in I_{\delta ^+}}\) be a sequence of weak solutions of the LLG, in the sense of Definition 2, and suppose that \({u}_{\varepsilon }(0) = u^{*}\) for some \(u^{*}(\xi ) \in H^1( S, {\mathbb {S}}^2)\). Since \(u^{*}\) does not depend on the \({s}\)-variable, from (12), we get the existence of a positive constant \(\kappa _{{{\mathcal {M}}}} \left( u^{*}\right) \), depending only on the volume of \({{\mathcal {M}}}\) and on \(\left\| {\nabla _{ \xi \,}}u^{*}\right\| ^2_{L^2 (S)}\), such that, for every \(\varepsilon > 0\)
Thus, due to the energy inequality (41), taking into account (9), we have that for every \(\varepsilon \in I_{\delta ^+}\)
In particular, recalling the expression of \({{\mathcal {F}}}_{\varepsilon }\) (cf. (24)), we get that for every \(\varepsilon > 0\) there holds:
By the previous uniform bounds, we infer the existence of a map \({u}_0 \in L^{\infty }({\mathbb {R}}^+ ; H^1 (S, {\mathbb {S}}^2 ))\), independent of the variable \({s}\), with \({u}_0 \in H^1 \left( S_T, {\mathbb {S}}^2 \right) \) for every \(T > 0\), such that, possibly for a subsequence, the following convergence properties hold true:
From Lemma 1 and (96), it follows that for every \(T \in {\mathbb {R}}_+\)
Also, by Aubin–Lions–Simon lemma, since the family
is uniformly bounded, we get that for every \(T \in {\mathbb {R}}_+\),
Taking the limit for \(\varepsilon \rightarrow 0\) of the expression of the effective field (36) we get that for every \(\varphi \in H^1 \left( {{\mathcal {M}}}_T,^{} {\mathbb {R}}^3 \right) \) which does not depend on the \({s}\)-variable,
Therefore, passing to the limit for \(\varepsilon \rightarrow 0\) in the family of LLG equation (40), we end up with the weak formulation of the limit LLG equation which reads, for every \(\varphi \in H^1 \left( S_T,^{} {\mathbb {R}}^3 \right) \), as
In particular, in the smooth setting, integrating by parts in (103), we get the strong form of the limiting LLG equations that read as
where \(- {\varvec{h}_{\textsf {eff} }^0}[ {u}_0 ] {:=}-_{\xi } {u}_0 + (n \otimes n) {u}_0\).
Finally, the energy inequality (44) is a direct consequence of the energy inequalities satisfied by the family of solutions \(\left( {u}_{\varepsilon } \right) _{\varepsilon \in I_{\delta ^+}}\):
Indeed, by the lower semicontinuity of the norms we have
and the right-hand side coincides with \({{\mathcal {F}}}_0 \left( u^{*}\right) \) because, as shown in Sect. 3.6, \(u^{*}\) is a recovery sequence for the \(\varGamma \)-limit \({{\mathcal {F}}}_0\). This completes the proof.
References
Acerbi, E., Fonseca, I., Mingione, G.: Existence and regularity for mixtures of micromagnetic materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 462, 2225–2243 (2006). https://doi.org/10.1098/rspa.2006.1655
Agranovich, M.S.: Sobolev Spaces, Their Generalizations and Elliptic Problems in Smooth and Lipschitz Domains. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-14648-5
Alouges, F., Di Fratta, G.: Homogenization of composite ferromagnetic materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 471, 20150365 (2015). https://doi.org/10.1098/rspa.2015.0365
Alouges, F., Labbé, S.: Convergence of a ferromagnetic film model. C. R. Math. 344, 77–82 (2007). https://doi.org/10.1016/j.crma.2006.11.031
Alouges, F., Soyeur, A.: On global weak solutions for Landau–Lifshitz equations: existence and nonuniqueness. Nonlinear Anal. 18, 1071–1084 (1992). https://doi.org/10.1016/0362-546X(92)90196-L
Bertotti, G.: Hysteresis in Magnetism: For Physicists, Materials Scientists, and Engineers. Academic Press, San Diego (1998)
Braides, A., Defranceschi, A.: Homogenization of Multiple Integrals, vol. 263. Clarendon Press, Oxford (1998)
Brown, W.F.: Micromagnetics. Interscience Publishers, London (1963)
Brown, W.F.: Magnetostatic Principles in Ferromagnetism. North-Holland Publishing Company, Amsterdam (1962)
Carbou, G.: Thin layers in micromagnetism. Math. Models Methods Appl. Sci. 11, 1529–1546 (2001). https://doi.org/10.1142/s0218202501001458
Dal Maso, G.: Introduction to \(\Gamma \)-Convergence, vol. 8. Birkhauser, Boston (1993)
Desimone, A.: Hysteresis and imperfection sensitivity in small ferromagnetic particles. Meccanica 30, 591–603 (1995). https://doi.org/10.1007/bf01557087
DeSimone, A., Kohn, R.V., Müller, S., Otto, F.: Recent analytical developments in micromagnetics. Sci. Hysteresis 2, 269–381 (2006)
DeSimone, A., Kohn, R.V., Müller, S., Otto, F.: A reduced theory for thin-film micromagnetics. Commun. Pure Appl. Math. 55, 1408–1460 (2002). https://doi.org/10.1002/cpa.3028
Di Fratta, G.: Dimension reduction for the micromagnetic energy functional on curved thin films. BCAM Technical Reports. https://bird.bcamath.org/handle/20.500.11824/337 (2016)
Di Fratta, G., Muratov, C.B., Rybakov, F.N., Slastikov, V.V.: Variational principles of micromagnetics revisited. SIAM J. Math. Anal. (2020), forthcoming
Di Fratta, G., Slastikov, V., Zarnescu, A.: On a sharp Poincaré-type inequality on the \(2\)-sphere and its application in micromagnetics. SIAM J. Math. Anal. 51, 3373–3387 (2019). https://doi.org/10.1137/19M1238757
Do Carmo, M.: Differential Geometry of Curves and Surfaces, 2nd edn. Prentice-Hall, Englewood Cliffs (2018)
Gaididei, Y., Kravchuk, V.P., Sheka, D.D.: Curvature effects in thin magnetic shells. Phys. Rev. Lett. 112(25), 257203 (2014). https://doi.org/10.1103/PhysRevLett.112.257203
Gilbert, T.L.: A Lagrangian formulation of the gyromagnetic equation of the magnetisation field. Phys. Rev. 100, 1243 (1955)
Gilbert, T.: A phenomenological theory of damping in ferromagnetic materials. IEEE Trans. Magn. 40, 3443–3449 (2004)
Gioia, G., James, R.D.: Micromagnetics of very thin films. Proc. R. Soc. A Math. Phys. Eng. Sci. 453, 213–223 (1997). https://doi.org/10.1098/rspa.1997.0013
Goussev, A., Robbins, J.M., Slastikov, V.: Domain wall motion in thin ferromagnetic nanotubes: analytic results. Europhys. Lett. (EPL) 105, 67006 (2014). https://doi.org/10.1209/0295-5075/105/67006
Hrkac, G., Pfeiler, C.-M., Praetorius, D., Ruggeri, M., Segatti, A., Stiftner, B.: Convergent tangent plane integrators for the simulation of chiral magnetic skyrmion dynamics. Adv. Comput. Math. 45, 1–40 (2019). https://doi.org/10.1007/s10444-019-09667-z
Hubert, A., Schäfer, R.: Magnetic Domains: The Analysis of Magnetic Microstructures. Springer, Berlin (2008)
Ignat, R.: A survey of some new results in ferromagnetic thin films. Sémin. Équ. Dériv. Partielles (Polytech.) 2007–2008 33, 1–19 (2007)
Jackson, J.D.: Classical Electrodynamics. Wiley, New York (1998)
Kohn, R.V., Slastikov, V.V.: Another thin-film limit of micromagnetics. Arch. Ration. Mech. Anal. 178, 227–245 (2005). https://doi.org/10.1007/s00205-005-0372-7
Landau, L., Lifshitz, E.: On the theory of the dispersion of magnetic permeability in ferromagnetic bodies. Perspect. Theor. Phys. 8, 51–65 (2012). https://doi.org/10.1016/b978-0-08-036364-6.50008-9
Landeros, P., Allende, S., Escrig, J., Salcedo, E., Altbir, D., Vogel, E.E.: Reversal modes in magnetic nanotubes. Appl. Phys. Lett. 90, 102501 (2007). https://doi.org/10.1063/1.2437655
Mark, A.G., Gibbs, J.G., Lee, T.C., Fischer, P.: Hybrid nanocolloids with programmed three-dimensional shape and material composition. Nat. Mater. 12, 802–807 (2013). https://doi.org/10.1038/nmat3685
Melcher, C., Sakellaris, Z.N.: Curvature stabilized skyrmions with angular momentum. Lett. Math. Phys. 109, 1–14 (2019). https://doi.org/10.1007/s11005-019-01188-6
Nédélec, J.-C.: Acoustic and Electromagnetic Equations: Integral Representations for Harmonic Problems, vol. 144. Springer, Berlin (2001)
Praetorius, D.: Analysis of the operator \(\Delta ^{- 1}\)div arising in magnetic models. Z. Anal. Anwend. 23, 589–605 (2004). https://doi.org/10.4171/ZAA/1212
Serpico, C., Bertotti, G., Mayergoyz, I.D., D’Aquino, M.: Nonlinear Magnetization Dynamics in Nanomagnets. Elsevier Science Limited, Amsterdam (2007)
Sheka, D.D., Makarov, D., Fangohr, H., Volkov, O.M., Fuchs, H., van den Brink, J., Gaididei, Y., Rößler, U.K., Kravchuk, V.P.: Topologically stable magnetization states on a spherical shell: curvature-stabilized skyrmions. Phys. Rev. B 94, 1–10 (2016). https://doi.org/10.1103/physrevb.94.144402
Slastikov, V., Sonnenberg, C.: Reduced models for ferromagnetic nanowires. IMA J. Appl. Math. 77, 220–235 (2012)
Slastikov, V.: Micromagnetics of thin shells. Math. Models Methods Appl. Sci. 15, 1469–1487 (2005). https://doi.org/10.1142/s021820250500087x
Sloika, M.I., Sheka, D.D., Kravchuk, V.P., Pylypovskyi, O.V., Gaididei, Y.: Geometry induced phase transitions in magnetic spherical shell. J. Magn. Magn. Mater. 443, 404–412 (2017). https://doi.org/10.1016/j.jmmm.2017.07.036
Smith, E.J., Makarov, D., Sanchez, S., Fomin, V.M., Schmidt, O.G.: Magnetic microhelix coil structures. Phys. Rev. Lett. 107, 097204 (2011). https://doi.org/10.1103/PhysRevLett.107.097204
Streubel, R., Makarov, D., Gaididei, Y., Schmidt, O.G., Kravchuk, V.P., Sheka, D.D., Kronast, F., Fischer, P.: Magnetism in curved geometries. J. Phys. D Appl. Phys. 49, 363001 (2016). https://doi.org/10.1088/0022-3727/49/36/363001
Visintin, A.: On Landau–Lifshitz equations for ferromagnetism. Jpn. J. Appl. Math. 2, 69–84 (1985). https://doi.org/10.1007/bf03167039
Weiss, P.: La variation du ferromagnétisme avec la température. C. R. l’Acad. Sci. 143, 1136 (1906)
Acknowledgements
Open access funding provided by Austrian Science Fund (FWF). The author acknowledges support from the Austrian Science Fund (FWF) through the special research program Taming complexity in partial differential systems (Grant SFB F65) and of the Vienna Science and Technology Fund (WWTF) through the research project Thermally controlled magnetization dynamics (Grant MA14-44).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Di Fratta, G. Micromagnetics of curved thin films. Z. Angew. Math. Phys. 71, 111 (2020). https://doi.org/10.1007/s00033-020-01336-2
Received:
Revised:
Published:
DOI: https://doi.org/10.1007/s00033-020-01336-2