Analytical Model for Tsunami Propagation Including Source Kinematics

Abstract

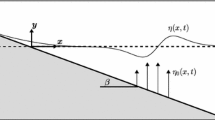
There are only a few analytical 2+1D models for tsunami propagation, most of which treat tsunami generation from a static deformation field isolated from the kinematics of the rupture. This work examines the behavior of tsunami propagation in a simple setup including a source time function which accounts for a time description of the rupture process on the tsunami source. An analytical solution is derived in the wavenumber domain, which is quickly inverted to space with the fast Fourier transform. The solution is obtained in closed form in the 1+1D case. The inclusion of temporal parameters of the source such as rise time and rupture velocity reveals a specific domain of very slow earthquakes that enhance tsunami amplitudes and produce non-negligible shifts in arrival times. The results confirm that amplification occurs when the rupture velocity matches the long-wave tsunami speed, and the static approximation corresponds to a limit case for (relatively) fast ruptures.

Appendices

Appendix 1: Detailed Mathematical Derivation

1.1 2+1D Case

In the following, detailed derivations are shown step by step. The classical solution for the irrotational long-wave tsunami approach in a constant ocean depth is

$$\begin{aligned} \overline{\widehat{{\eta }}}(k_x,k_y,s) = \frac{s^2}{s^2 + \omega ^2} \frac{\overline{\widehat{{\zeta }}}(k_x,k_y,s) }{\cosh (kh)} \end{aligned}$$

(8)

where $\omega ^2 = gk\tanh (kh)$, $k^2 = k_x^2 + k_y^2$, g is the gravity acceleration and h is the ocean depth. The seafloor displacement is modeled as

$$\begin{aligned} \zeta (x,y,t) = \zeta ^x_0(x)\zeta ^y_0(y)T(y,t) \end{aligned}$$

(9)

with

$$\begin{aligned} T(y,t) = S\left( \frac{t - t_V(y)}{t_R}\right) , \end{aligned}$$

(10)

with the function $S(x) = x{\mathcal {H}}(x(1-x)) + {\mathcal {H}}(x-1)$.

Firstly, we compute the Fourier–Laplace transform of T. Note that

$$\begin{aligned} {\mathcal {L}}\{S\}(s) = \frac{1}{s^2}\left( 1 - e^{-s}\right) . \end{aligned}$$

(11)

Then, by the Laplace transform properties of time shift and scaling, we obtain

$$\begin{aligned} \begin{aligned} {\mathcal {L}}\{T\}(s)&= t_R\,{\overline{S}}\left( t_R s\right) e^{-t_V(y)s} \\&= \frac{1}{t_Rs^2}\left( 1 - e^{-s t_R}\right) e^{-t_V(y)s} \end{aligned}. \end{aligned}$$

(12)

Now we need to compute the following Fourier transform:

$$\begin{aligned} {\mathcal {F}}\left\{ \zeta ^y_0(y)e^{-t_V(y)s}\right\} (k_y), \end{aligned}$$

(13)

which depends on the rupture model. In this case, a general bidirectional propagation is chosen.

The origin of the coordinate system is set at the starting rupture point. The rectangular fault is then divided into two parts, one segment to the north of length $L_2$ and one segment to the south of length $L_1$, accounting for the total length $L = L_1 + L_2$. Thus, $\zeta ^y_0(y) = {\mathcal {H}}\left( (L_2 - y)(y + L_1) \right)$ and $t_V(y) = \frac{|y|}{V_r}$. Computation of expression (13) results in

$$\begin{aligned}&{\mathcal {F}}\left\{ \zeta ^y_0(y)e^{-t_V(y)s}\right\} (k_y) = \int _{-L_1 }^{L_2}e^{-\frac{s}{V_r}|y| + ik_yy}dy\\&\quad = \int _{-L_1}^{0}e^{\frac{s}{V_r}y + ik_yy}dy + \int _{0}^{L_2}e^{-\frac{s}{V_r}y + ik_yy}dy\\&\quad = F\left( \frac{s}{V_r},k_y, 0\right) - F\left( \frac{s}{V_r},k_y, -L_1\right) + F\left( -\frac{s}{V_r},k_y, L_2\right) - F\left( -\frac{s}{V_r},k_y, 0\right) \end{aligned}$$

where $F(a,b,x) = \frac{e^{ax}}{a^2 + b^2}\big [\big (a\cos (bx) + b\sin (bx)\big ) + i\big ( a\sin (bx) - b\cos (bx) \big )\big ]$.

Inserting in Eq. 8,

$$\begin{aligned}&\overline{\widehat{{\eta }}}(k_x,k_y,s) = \frac{\widehat{\zeta ^x_0}(k_x)}{\cosh (kh)} \frac{V_r^2}{t_R}\left( 1 - e^{-t_Rs}\right) \frac{1}{s^2 + \omega ^2}\nonumber \\&\quad \times \frac{1}{s^2 + (k_yV_r)^2}\left[ \, \frac{2}{V_r}s \, + e^{-\frac{L_2}{V_r}s}\left\{ -\frac{s}{V_r}\cos (L_2k_y) + k_y\sin (L_2k_y) \right\} \right. \nonumber \\&\quad - e^{-\frac{L_1}{V_r}s}\left\{ \frac{s}{V_r}\cos (L_1k_y) - k_y\sin (L_1k_y) \right\} + ie^{-\frac{L_2}{V_r}s}\left\{ -\frac{s}{V_r}\sin (L_2k_y) - k_y\cos (L_2k_y) \right\} \nonumber \\&\quad \left. + ie^{-\frac{L_1}{V_r}s}\left\{ \frac{s}{V_r}\sin (L_1k_y) + k_y\cos (L_1k_y) \right\} \right] \end{aligned}$$

(14)

Since ${\mathcal {L}}\left\{ \sin (at){\mathcal {H}}(t)\right\} (s) = \frac{a}{s^2 + a^2}$, we can define $q(a,b,t) =: \frac{{\mathcal {H}}(t)}{a^2 - b^2 }\left( \frac{\sin (bt)}{b} - \frac{\sin (at)}{a}\right)$, and then we have that ${\overline{q}}(a,b,s) = \frac{1}{s^2 + a^2}\cdot \frac{1}{s^2 + b^2}$, with $a = \omega$ and $b = k_yV_r$.

Defining $p(a,b,t,t_0) =: {\mathcal {L}}^{-1}\{se^{-st_0}{\overline{q}}(a,b,s)\}(t) = \partial _t q(a,b,t-t_0)$ and using the properties of the Laplace transform, Eq. 15 can be rewritten in terms of q and p (function arguments are omitted for the sake of simplicity)

$$\begin{aligned} {\widehat{\eta }}(k_x,k_y,t) = \frac{\widehat{\zeta ^x_0}(k_x)}{\cosh (kh)} \frac{V_r^2}{t_R}\left[ \phi (t) - \phi (t - t_R)\right] \end{aligned}$$

(15)

where

$$\begin{aligned} \phi (t)= & {} \frac{2}{V_r}p(t,0) -\frac{1}{V_r}\cos (L_2k_y)p(t,t_2) + k_y\sin (L_2k_y)q(t-t_2) \nonumber \\&-\frac{1}{V_r}\cos (L_1k_y)p(t,t_1) + k_y\sin (L_1k_y)q(t-t_1)\nonumber \\&+ i\left\{ -\frac{1}{V_r}\sin (L_2k_y)p(t,t_2) - k_y\cos (L_2k_y)q(t-t_2) \right. \nonumber \\&\left. + \frac{1}{V_r}\sin (L_1k_y)p(t,t_1) + k_y\cos (L_1k_y)q(t-t_1) \right\} \end{aligned}$$

(16)

and $t_i = \frac{L_i}{V_r}, \, i \in \{1,2\}.$ Note that there are removable singularities in functions p and q when $\omega = V_rk_y$.

The static deformation can be retrieved by letting $V_r \rightarrow \infty$ and $t_R \rightarrow 0$, which gives

$$\begin{aligned} {\widehat{\eta }}(k_x,k_y,t) = \frac{\widehat{\zeta _0^x}(k_x)}{k_y\cosh (kh)}\left[ \sin (k_yL_2) + \sin (k_yL_1) + i\{\cos (k_yL_1) - \cos (k_yL_2)\} \right] \cos (\omega t). \end{aligned}$$

(17)

Observe that the symmetric bilateral case has no frequency shifts and leads to a pure real spectrum

$$\begin{aligned} {\widehat{\eta }}(k_x,k_y,t) = L\frac{\widehat{\zeta _0^x}(k_x)}{\cosh (kh)}\text {sinc}\left( \frac{k_yL}{2}\right) \cos (\omega t). \end{aligned}$$

(18)

Finally, the water surface is inverted with a fast Fourier transform (FFT) algorithm:

$$\begin{aligned} \eta (x,y,t) = {\mathcal {F}}^{-1}\left\{ {\widehat{\eta }}(k_x,k_y,t)\right\} (x,y). \end{aligned}$$

1.2 1+1D Case

If 2D effects are neglected, $\zeta _0^x(x) = H$ and $\widehat{\zeta ^x_0}(k_x) = 2\pi \delta (k_x)$. Equation (16) then becomes

$$\begin{aligned} {\widehat{\eta }}(k_y,t) = \frac{H}{\cosh (k_yh)}\frac{V_r^2}{t_R}\left[ \phi (t) - \phi (t - t_R)\right]. \end{aligned}$$

(19)

Again, the final solution $\eta (y,t)$ can be retrieved from Eq. (20) with the 1D FFT.

In order to better understand analytically the behavior of the amplification as a function of rupture velocity, only a unidirectional rupture is treated with a instant rise time, that is to say, $L_1 = 0, L_2 = L$ and $t_R = 0$. Equation (20) becomes

$$\begin{aligned} {\widehat{\eta }}(k_y,t) = \frac{H}{\cosh (k_yh)}V_r^2\phi '(k_y,t) \end{aligned}$$

(20)

with

$$\begin{aligned} \phi '(k_y,t)= & {} \, \frac{1}{V_r}p'(t,0) - \frac{1}{V_r}\cos (Lk_y)p'(t,t^*) + k_y\sin (Lk_y)q'(t - t^*) \nonumber \\&+ i\left\{ -\frac{1}{V_r}\sin (Lk_y)p'(t,t^*) - k_y\cos (Lk_y)q'(t-t^*) + k_yq'(t)\right\} \end{aligned}$$

(21)

and $t^* = L/V_r$. To make possible the derivation of an analytical solution, it is necessary to neglect the dispersive effects: $\omega (k_y) \approx ck_y$.

Performing the inverse Fourier transform term by term, by symmetry, each is of the form

$$\begin{aligned} \psi (x,y) = \int _0^\infty \frac{\sin (k_yx)\cos (k_yy)}{k_y\cosh (k_yh)}dk_y = \arctan \left( \frac{\sinh \left( \frac{\pi x}{2h}\right) }{\cosh \left( \frac{\pi y}{2h}\right) }\right). \end{aligned}$$

(22)

Thus, the solution is

$$\begin{aligned} \eta (y,t)= & {} \frac{\nu ^2H}{\pi (1-\nu ^2)}\left[ \psi \left( y-V_rt,0\right) + \psi (ct-y,0) + \left( \frac{1}{\nu }-1\right) \psi (ct,y)\right. \nonumber \\&+ {\mathcal {H}}(t')\left\{ \psi \left( L+V_rt'-y,0\right) \right. \nonumber \\&\left. \left. - \frac{1}{2}\left( \frac{1}{\nu }-1\right) \psi \left( y-L+ct',0\right) + \frac{1}{2}\left( \frac{1}{\nu }+1\right) \psi \left( y-L-ct',0\right) \right\} \right] \end{aligned}$$

(23)

where $t' = t - t^*$.

In particular, when $\nu$ tends to 1 $(V_r = c)$, the maximum amplification at the end of the fault is

$$\begin{aligned} \frac{\eta \left( L,\frac{L}{c}\right) }{H} = \frac{L}{4h} + \frac{1}{2\pi }\psi (L,L) \approx \frac{L}{4h} + \frac{1}{8}. \end{aligned}$$

(24)

Appendix 2: Derivation of Function $\psi ({x,y})$

First, for any $h>0$, let us define the function $\varphi (x)$ as follows:

$$\begin{aligned} \varphi (x) = \int _{0}^{\infty }\frac{\sin (kx)}{k\cosh (kh)}dk. \end{aligned}$$

(25)

Then,

$$\begin{aligned} \psi (x,y) = \frac{1}{2}\left[ \varphi (x+y) - \varphi (y-x) \right]. \end{aligned}$$

(26)

By the Leibniz rule,

$$\begin{aligned} \partial _x \varphi (x) = \int _{0}^{\infty }\frac{\cos (kx)}{\cosh (kh)}dk \end{aligned}$$

(27)

The integral 28 can be easily evaluated by standard complex contour integration. For this type of integral, the contour is the rectangle defined by the corners (R, 0); $\left( R,\frac{\pi i}{h}\right)$; $\left( -R,\frac{\pi i}{h}\right)$; $(-R,0)$ enclosing a simple pole at $\frac{\pi i}{2h}$, satisfying the convergence conditions.

Therefore, by the residue theorem,

$$\begin{aligned} \partial _x \varphi (x) = \frac{\pi }{2h}\text {sech}\left( \frac{\pi x}{2h}\right). \end{aligned}$$

(28)

Since $\varphi (0) = 0$ and $\int \text {sech}(ax)dx = \frac{1}{a}\arctan (\sinh (ax))+C$, integration of (28) allows us to retrieve $\varphi$:

$$\begin{aligned} \varphi (x) = \arctan \left( \sinh \left( \frac{\pi x}{2h}\right) \right) . \end{aligned}$$

(29)

By using the property $\arctan (a) \pm \arctan (b) = \arctan \left( \frac{a\pm b}{1 \mp ab}\right)$, it is equivalent to write

$$\varphi (x) = 2\arctan \left( e^{\frac{\pi x}{2h}}\right) - \frac{\pi }{2}.$$

(30)

. Finally, replacing in( 27) and manipulating the arguments, the result holds.