Abstract
Co-seismic volumetric changes are often interpreted as tensile fracturing in response to fluid injection during geothermal reservoir stimulation. Such volumetric changes manifest themselves as isotropic moment tensor components, which may thus constitute a measure for hydraulic stimulation efficiency. Recent analyses found significant isotropic moments of M2+ earthquakes during the 2006 hydraulic stimulation of a geothermal reservoir in Basel, Switzerland. The results contradicted first-motion focal mechanisms, which are in close agreement with shear sources without volumetric changes. Here we revisit the magnitude 1.7+ Basel events with full and stochastic moment tensor inversions in order to provide additional and/or supporting evidences for the occurrence of volumetric sources, if any. We furthermore apply purely deviatoric, and superimposed tensile and shear fault mechanisms, which we believe are meaningful constraints for fluid-induced earthquakes. As a result, we only find a single earthquake with statistically significant volumetric faulting. Spatial and temporal patterns of fluid-induced sources therefore have to be taken as indicative only, even though they suggest a clear relationship between fluid injections and fault mechanisms. On the other hand, we confirm that most inverted moment tensors (including the statistically significant one) show some inconsistencies with first motion focal mechanisms. We suggest that this is a manifestation of a more complicated fault geometry, which none of our moment tensor constraints can describe.
Similar content being viewed by others
1 Introduction
In 2006 an enhanced geothermal project was initiated in the city center of Basel, Switzerland (Fig. 1). About 12,500 m3 of pressurized water were injected between December 2nd and December 8th (Deichmann and Giardini 2009) until a local magnitude (ML) 2.6 earthquake exceeding successive levels of alert occurred. After the injection stopped, other earthquakes as large as ML3.4 occurred on the same day (Table 1). The seismicity was located at depths comparable to the 5 km-deep well and continued in the next weeks to months with a total of four ML3+ earthquakes between December 2006 and May 2007 (Table 1). This sequence provides one of the best datasets to study the effect of fluid injection on earthquake source mechanisms given the brief injection period, the relatively large magnitude of recorded events, the low seismicity rate prior to injection, and the good quality of the seismic records from both local and regional stations operated by the Swiss Seismological Service.
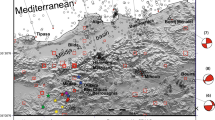
Map of the seismicity recorded in the vicinity of Basel (a) and of the strong-motion stations used in the study (b). a Earthquakes from December 2006 to end of November 2007 (Deichmann and Ernst 2009) in gray are shown together with the full moment tensor solutions of ML1.7+ earthquakes. The beach ball mechanisms are color-coded by their absolute isotropic component (color saturation at 20 %). Red triangle indicates the injection site. b Blue triangles show the strong-motion stations used in the study. The red box shows the area depicted in a. c Cross-section (AB) shows the depth distribution of the events
In general, fluid-induced earthquakes, such as the Basel events, may involve volumetric faulting in addition to shear dislocation (Fischer and Guest 2011). This volumetric faulting expresses itself by either pure tensile fractures or hybrid events combining tensile and shear fracturing with common fault planes. These fault processes can be understood with the help of the Mohr circle. As the injection of fluids increases the fluid pore pressure at depth, the Mohr circle is shifted in the negative normal stress direction until it touches the fracture envelope of the local rock mass. Depending on the location of this contact point in the normal/shear stress plane, the resultant fractures are either pure shear events, hybrid shear and tensile fractures, or pure tensile fractures. These last events are rare to observe, requiring small enough differential stress (difference between minimum and maximum normal stresses), which is less likely to occur with increasing depths (Fischer and Guest 2011).
Moment tensor inversions are capable of detecting volumetric changes during purely tensile or shear-tensile hybrid events. Such volumetric changes can be caused by fluid injection and manifest themselves as a non-zero isotropic moment tensor, whose monitoring has received particular attention in the context of induced seismicity (Ross et al. 1996; Cuenot et al. 2006; Sileny et al. 2009; Johnson 2014a; Guilhem et al. 2014). Modeling these events and quantifying the proportion of their volumetric component due to the movement of fluids in the ground constitute a major step toward better describing the link between induced earthquakes and fluid injection. Changes in the faulting style of induced earthquakes during a given sequence also highlight fluid propagation and stress conditions at depth. Unfortunately, numerical instabilities of moment tensor inversions caused by oversimplified seismic velocity models, noisy data and poor station coverage can often introduce spurious isotropic components (Rössler et al. 2007; Ford et al. 2009a; Ben-Zion and Ampuero 2009).
Zhao et al. (2014) recently presented evidence for isotropic moment tensor components for the Basel events. While statistical tests supported the robustness of their results, three key questions remain unanswered. First, can these results be represented with alternative inversion schemes, whose moment tensor constraints are particularly suitable for fluid-induced tensile faulting? Second, why do the full moment tensor solutions of Zhao et al. (2014) and previously determined first-motion focal mechanisms (Deichmann and Ernst 2009; Deichmann and Giardini 2009) show disagreement? Third, compared to first-motion focal mechanisms and double-couple (‘pure shear’) moment tensors, why do full moment tensors provide a significantly better waveform fit for events occurring during a later period, i.e., at a time when the geothermal reservoir had returned to a tectonic regime characterized by shear faulting alone according to the previous study? Regarding the latter question, one would instead expect that once the injection stops, pore pressure at depth should progressively decrease and the differential stress increase again, leading to pure shear faulting events. An inversion constrained to a double-couple (pure shear) or a deviatoric (non-volumetric) moment tensor should thus be able to perfectly represent the source mechanism of the earthquakes after injection without the need to invoke the full, unconstrained moment tensor approach.
These open questions motivate the present moment tensor investigation of an extended set of the Basel sequence earthquakes. We invert for the source of the 28 magnitude 1.7+ events presented by Deichmann and Ernst (2009) that include all of the 19 magnitude 2.0+ earthquakes previously analyzed by Zhao et al. (2014). This extended dataset, which offers a broader picture of the Basel system, and our different but robust inversion schemes provide independent constraints on the earthquake sources. In contrast to Zhao et al. (2014), we test the performance of constrained moment tensors representing general non-volumetric and superimposed tensile and shear mechanisms. We argue that these fault mechanisms are more relevant to induced seismicity, because they include several specific source models for fluid-induced fracturing and they provide a quantitative estimate for co-seismic void space creation during hydraulic stimulation. Our results confirm the discrepancy between moment tensor solutions and some first-motion polarities suggesting possible finite source effects and/or other complexities in the source process. At the same time even though we observe compound sources, our determined isotropic components show a lower significance level than those of Zhao et al. (2014), especially in the later part of the seismic sequence when the injection has stopped. Nevertheless, qualitative results supported by stochastic moment tensor inversions and source type plots suggest a clear influence of fluid injection on non-shear fault mechanisms in agreement with the findings of Zhao et al. (2014). Therefore, our study yields both support for and some disagreement with the findings of Zhao et al. (2014), which stimulates an interesting discussion on source mechanisms of induced earthquakes.
2 Data and methods
2.1 Data and seismic velocity model
We perform the source analysis of all ML1.7+ earthquakes (Table 1) for which first-motion focal mechanisms and high-precision relative locations exist between December 2006 and May 2007 (Deichmann and Ernst 2009; Deichmann et al. 2014). The events are located at depths between 3.9 and 5.0 km (Table 1). The analysis is limited to strong-motion stations from the SED network, which were operational during our entire study period and which locate within 6 km of the event epicenters (stations SBAF, SBAP, OTTER, SBIS, and SRHB shown in Fig. 1b). The latter condition facilitates using a 1D seismic velocity model (Model 2 in Deichmann and Ernst 2009) despite lateral variations of the subsurface structure in the Basel area. The 1D velocity model (Table 2) combines information about P-wave velocities and layer thicknesses provided by Deichmann and Ernst (2009), and corresponding S-wave velocities from the local 1D velocity model of Ripperger et al. (2009). It also respects the condition of an average Vp/Vs ratio of 1.7, predominant in the Basel region (Ripperger et al. 2009).
Seismograms are decimated to 125 Hz, rotated and integrated to displacement. A two-pass, four-pole Butterworth filter with a 0.5–3 Hz passband provides the best compromise between reducing the effects of the simplified 1D seismic velocity model and maximizing the signal-to-noise ratio (SNR). The waveforms processed in this way show a dominant S-wave (Fig. 2), which is well pronounced on the radial component, because earthquake focal depths are comparable to station-epicenter distances. Equivalently, P-waves are particularly strong on the vertical component (Fig. 2).
Seismograms of event 113 (ML 2.5) recorded at Stations OTTER (a) and SBIS (b). Top panels show unfiltered acceleration seismograms, bottom panels show bandpass filtered (0.5–3 Hz) displacement seismograms. ‘OT’ corresponds to origin time. Note the impulsive P-wave arrival visible in the unfiltered data. In the bandpass filtered data, the horizontally polarized S-wave dominates the seismograms
2.2 Moment tensor inversions
We use a multi-step procedure to characterize the earthquake sources. First, employing a least-square approach, we use TDMT_INV (Dreger, 2003) to compute moment tensors in the time domain, and we first invert for the deviatoric moment tensors, which decompose into a double-couple (DC) tensor representing pure shear dislocation and a compensated linear vector dipole (CLVD) tensor (Jost and Herrmann 1989). TDMT_INV is a standard software package that is used to calculate regional moment tensors in California, Switzerland, and other regions (Baer et al. 2007; Minson and Dreger 2008; Scognamiglio et al. 2009). The inversion is based on the point-source approximation in space and time. Accordingly, the ground motion vector d can be expressed in terms of the Green’s function tensor, G, and the moment tensor M of the source:
The Green’s functions are calculated for specific force-couple orientations using the frequency-wavenumber integration code (FKRPROG) of Saikia (1994) based on the method of Wang and Herrmann (1980). Least-square inversions are performed on the three components of all stations considered for each earthquake. The number of stations inverted for individual sources depends on the quality of the waveforms in terms of SNR in the bandpass filter and their goodness of fit. We subsequently invert for the full moment tensor. This latter inversion allows for a non-zero isotropic component representing co-seismic volumetric change of the source. The decomposition of the recovered earthquake sources into isotropic, double-couple, and CLVD moment tensors follows the approach proposed by Bowers and Hudson (1999) and Jost and Herrmann (1989). The full moment tensor, M, is defined as the sum of the isotropic moment tensor, MISO, and the deviatoric moment tensor, MDEV:
MDEV decomposes into MDC and MCLVD:
The percentages of the isotropic (pISO), double-couple (pDC), and CLVD (pCLVD) components are then defined following Vavryčuk (2001).
For events with an absolute isotropic component larger than 15 %, we apply a third inversion scheme that constrains the moment tensor to a crack-plus-double-couple form (CDC, Minson et al. 2007). These constrained moment tensors represent the aforementioned hybrid events, i.e., superimposed shear and tensile motion along common fault planes (Vavryčuk 2001; Minson et al. 2007; Tape and Tape 2012). Though somewhat arbitrary, the 15 % threshold targets source mechanisms, whose departures from pure shear faulting unlikely result from numerical uncertainties alone. Indeed, because for the great majority of tectonic earthquakes the isotropic components tend to be very limited (i.e., less than 10 %, e.g., Kawakatsu 1991), an indication of volumetric changes by more than 15 % constitutes a conservative threshold for investigating isotropic components. To do so, we implement the CDC inversion with a grid search, which maximizes agreement between data and synthetics. First, we search for the strike, rake and dip of the shear mechanism with 20° increments. The double-couple moment is varied between 0 and 2 Mtot, defined as the moment obtained with the full moment tensor inversion at increments fixed to Mtot/10. The isotropic moment of the crack component is varied by the same increments, between –Mtot and +Mtot to allow for tensile opening and closing mechanisms. Subsequently, the fault plane search is refined to 2° around the orientation obtained in the previous step. In a third step, we refine increments of the double-couple moment and the isotropic moment of the crack component to Mtot/100.
Compared to the full moment tensor inversion, which has six free parameters, the deviatoric and CDC inversions reduce the solution space by one dimension. This stabilizes the inversions, typically at the expense of fit quality (Minson et al. 2007). The fit quality of all inversions is given by the variance reduction (VR):
As the Green’s functions are calculated for an idealized 1D velocity model, data and synthetics are visually aligned to maximize the variance reduction for each deviatoric inversion. This alignment is then kept constant in the full moment tensor and CDC inversions.
As pointed out by Zhao et al. (2014), the moment tensor inversions are primarily sensitive to the dominant S-waves. However, considering that pure volumetric sources should theoretically only emit P-waves, the utility of our inversion scheme for determination of co-seismic volumetric changes could thus be questioned. We argue that our approach is still valid for two reasons. First, as shown in Fig. 2, the radial component carries substantial amount of S-wave energy corresponding to SV polarization. However, SV waves also contain P-wave energy, which is converted via reflections and transmission at layer interfaces, and can therefore resolve isotropic moment tensor components. We confirm this assertion in Fig. 3, which shows an S-wave based and a P-wave based inversion, both determining similar isotropic components (31 % as opposed to 29 %) for an event of the studied period. The second argument for using S-waves is based on the general property that CDC moment tensors decompose into an isotropic and a CLVD moment tensor. The relative strength of these components is determined by the medium’s Poisson’s ratio (Walter et al. 2009). Consequently, for the CDC inversion, S-wave radiation constrains the strength of the CLVD term, which in turn constrains the isotropic moment.
Full moment tensor solutions for event 113. a Full moment tensor solution using both P and S waves. Inversion of 3 s long, 3 component displacement records of 5 stations filtered between 0.5 and 3 Hz. b Full moment tensor solution using only P waves on the vertical components filtered between 2 and 6 Hz. Both solutions return similar source decomposition
Our 28 events are an extension of the dataset of Zhao et al. (2014), who used all 19 M2+ earthquakes of the sequence, as well as additional stations. Even though the Basel project induced a large amount of seismic events, we refrain from inverting smaller magnitude earthquakes because such events suffer from a lower SNR in the considered passband. For our M1.7+ events, Fig. 4 shows the systematic decrease of SNR with decreasing local magnitude ML. Our SNRs for each component are calculated as the average of the ratio of the amplitude root-mean-squares within a 3 s noise and a 3 s signal window for each station. Most of our inverted events have SNRs above five, which corresponds to a threshold below which recovery of the isotropic component was found limited in regional moment tensor inversion (Fig. 7 in Ford et al. 2009b). Consequently, events with lower magnitudes are unsuitable for this study of co-seismic volumetric changes considering the source-station distance ranges and the filter applied. Inversions of weaker events would substantially decrease the number of available stations, and by thus, our confidence in the solutions.
Signal to noise ratio (SNR) in relation to local magnitude ML for all three components of the analyzed events. An SNR of 5 is a reasonable threshold for assuring recovery of the isotropic moment tensor component at regional distances (Ford et al. 2009b)
Our sets of inversion constraints are particularly suited for induced earthquakes. The reason is that the deviatoric inversion allows for a CLVD component, representing volumetric expansions, which are compensated by fluid flow or other processes (Kanamori et al. 1993; Konstantinou et al. 2003; Tkalčić et al. 2009). Similarly, the CDC constraint allows for co-seismic tensile faulting triggered by elevated pore pressures during fluid injection. In contrast to the deviatoric constraint, it can describe an overall volumetric change during earthquake rupture. Finally, in the context of the CDC constraint, co-seismic volumetric changes can be calculated from the moment tensor, providing a quantitative estimate of void space creation during hydraulic stimulation.
2.3 Statistical tests
In contrast to the full moment tensor with six free parameters (all independent elements of a symmetric 3 by 3 matrix), the deviatoric moment tensor is subject to one constraint (i.e., vanishing trace) and thus has 5 free parameters. It is therefore necessary to test whether the full moment tensor inversion provides a statistically significant improvement with respect to the deviatoric inversion. We apply the F-test criteria following the method presented by Templeton and Dreger (2006). For all events, we calculate F-test confidence levels by considering the VRs of both solutions, the number of stations used in the inversions, the number of inverted samples (i.e., 375), the low-pass corner frequency of the bandpass filter (i.e., 3 Hz), and the numbers of free parameters (i.e., 5 or 6). Full moment tensor solutions are considered statistically significant compared to the deviatoric solutions when the F-test confidence level reaches 95 % (Templeton and Dreger 2006). The same statistical test was used by Zhao et al. (2014), but it served to compare the significance of the full moment tensor solutions compared to the double-couple ones only (i.e., no CLVD involved).
2.4 Network sensitivity analysis
The final step in our moment tensor analysis stochastically probes a large number of random moment tensors to determine the likelihood of deviatoric and non-deviatoric solutions. As we are only interested in fault type (e.g., shear, CLVD, explosion) we disregard fault geometry. Rather than the standard beachball diagrams we instead use source-type plots (Fig. 5). The source-type plot representation, also called Hudson diagram (Hudson et al. 1989) visualizes the two parameters κ and ε. These parameters represent the strength of a moment tensor’s isotropic component and the departure of the deviatoric component from a pure shear mechanism, respectively (Julian et al. 1998). These two parameters are given by:
and
where |m′1| < |m′2| < |m′3| are the principal deviatoric moments (Jost and Herrmann 1989). For a deviatoric source (i.e., in the absence of any volumetric change), ε ranges from zero for a pure double-couple to ±0.5 for a pure CLVD. κ, on the other hand is a measure of the volume change. The ε and κ axes are skewed, such that any given area within the grid is proportional to the probability that a random moment tensor lies within this area. A pure double-couple mechanism resides in the center of the source type plot (ε,κ) = (0,0), and a pure explosion at its very top (ε,κ) = (0,1) (Fig. 5). CDC solutions lie on the straight line connecting the tensile and shear dislocations.
Distribution of the 28 full moment tensor solutions (black dots) in the Hudson source-type plot. The events are represented using their ε and κ values that correspond to the departure of the deviatoric component from a pure shear mechanism, and to the strength of the isotropic component, respectively. The blue line shows the range of possible solutions for deviatoric moment tensors distributed between the double-couple (DC) and CLVD regions. The green line shows the range of possible solutions for the crack-double-couple (CDC) moment tensors, and the red line shows the DC-isotropic sources
Following Ford et al. (2009a) and Guilhem et al. (2014), we realize the stochastic moment tensor modeling by generating a large number (100 million) of random moment tensors, whose synthetics are compared with the observed waveforms in the 0.5–3 Hz passband, and for which κ and ε are calculated. This analysis is called Network Sensitivity Solution (NSS; Ford et al. 2009a). These random moment tensors represent all types of sources, from pure double-couple to explosive/implosive sources, and include sources with mixed decomposition. In order to visualize the results, VRs are calculated for all random tensors, and solutions are represented in the Hudson diagram according to their fits. The large number of moment tensors provides enough waveform fits with large VRs. Such high-quality solutions define significance clusters of solutions in Hudson source-type plots (Hudson et al. 1989; Ford et al. 2009a; Guilhem et al. 2014), which permit earthquake source characterization. The clusters of solutions highlight moment tensors that produce similar seismogram fits. These are normalized with respect to the maximum VR that is obtained over the 100 million random tensors tested. In contrast to the representation of single κ and ε couples for individual events that are commonly presented in published studies (e.g., Ross et al. 1996; Zhao et al. 2014), this method illuminates some of the uncertainties in the source characterization as a large number of moment tensors with different source type can provide similar fits. The clusters can thus be used to determine whether the studied earthquakes deviate from pure double-couple solutions (Ford et al. 2009a; Guilhem et al. 2014).
3 Results
3.1 Predominance of shear mechanisms
Shear fault plane orientations of the deviatoric, full and CDC moment tensor inversions (Figs. 6, 7) are generally in good agreement with those derived from first-motion focal mechanisms (Deichmann and Ernst 2009). The moment magnitudes (Mw in Table 3) also agree with local magnitudes following known scaling relationships in Switzerland (Goertz-Allmann et al. 2011).
Summary of the moment tensor analysis for events 5–105: P-wave first-motion mechanisms (Deichmann and Ernst 2009), deviatoric solution, full moment tensor solutions, and crack-double-couple (CDC) solution. The plane projections in the beachball diagrams of the solutions are derived from the double-couple components of the inverted moment tensor. The green dots show negative P-wave polarities and the blue dots positive polarities (Deichmann and Ernst 2009). The variance reductions are indicated next to the beachballs
Summary of the moment tensor analysis for events 108–185. See Fig. 6 for additional explanation
None of the 28 studied earthquakes of the Basel sequence shows dominant volumetric co-seismic expansion or contraction, which would be indicated by source types near the vertical maxima of |κ| = 1. For most events, the full solutions cluster near the center of the source type plot (Fig. 5). This is in agreement with the statistical insignificance of the fit improvement between full and deviatoric moment tensor solutions for all but event 113 (Table 4). The strongest isotropic component is indeed found for event 113 and amounts to 31 % in the full moment tensor inversion (Table 4; Fig. 3). However, for more than 50 % of the studied earthquakes, the full moment tensor inversion finds isotropic proportions lower than 10 % (Table 4; Fig. 1). This supports the idea of predominantly non-volumetric ruptures during the 2006–2007 period in Basel, which is in agreement with the quadrantal distribution of P-wave polarities of the 28 earthquakes (Deichmann and Ernst 2009).
3.2 Events with isotropic components
With the strongest isotropic component and a 99.9 % F-test confidence level, event 113 is the only event to pass the 95 % threshold (Templeton and Dreger 2006). The significance levels of the remaining events range from ~50 to 90 %, with the majority below 70 % (Table 4; Fig. 8). To bolster the finding of a significant isotropic component for event 113, we perform jackknife tests examining the effects of removing selected stations from the moment tensor inversion. For this event, deviatoric and full moment tensor inversions initially use a total of five stations. This limited number of stations and this asymmetric distribution could potentially result in spurious moment tensor solutions. We then test the solution sensitivity to the removal of one and two stations (Fig. 9). All jackknife solutions show positive κ values, with a cluster in the vicinity of the solution obtained using 5 stations. The combinations of stations that give the lowest κ values have the common feature of missing station SBIS. Even though the change in κ is less important, the absence of the waveforms of station SBAP also affects the solution (Fig. 9). SBAP and SBIS are located about 2.5 and 4.7 km away from the source, respectively, and sample slightly different parts of the source radiation (Fig. 1). Removal of OTTER, SBAF, and SRHB has a weaker effect, probably because they locate at similar azimuths. This test demonstrates that even if the station configuration is altered, the source mechanism of event 113 deviates from a pure double-couple solution with a positive volumetric change.
Comparison of the isotropic components found in this study with those calculated by Zhao et al. (2014) for the 19 common events. Each event is color coded by its F-test value between deviatoric and full moment tensor solutions. Black colors indicated an F-test value below 50 %. The solid line shows the 1:1 ratio, and the dashed lines show the zone of agreement ±5 %. The stars on the left provide a complete list of the 28 events analyzed in this study
Hudson representation of the results of the jackknife test performed for event 113. The red triangle shows the solution when using all 5 stations. The blue symbols show solutions when station SBIS is not used. Same for the magenta symbols but for station SBAP. The green symbols show all the other station combinations. Squares show solutions when using sets of 4 stations, and circles when using sets of 3 stations. All the solutions indicate positive isotropic motion, and deviate from the center of the plot (double-couple region)
Despite the fact that only event 113 meets the formal 95 % criteria in the F-test, it is interesting to analyze the solutions of the six >15 % isotropic component events (events 5, 82, 94, 113, 147, 162), which also show the highest significance F-test levels for fit improvement when using the full moment tensor inversion (>78 %, including three events with >85 %). For these six earthquakes CDC solutions are computed. Despite the predominant double-couple mechanisms, the source types of the full, CDC and NSS solutions show variability among events (Fig. 10). The CDC solutions for the six events with more than 15 % isotropic components have positive κ values, except for the minor negative κ value of event 5 (Fig. 10). On the other hand, the full and NSS solutions return both positive and negative κ and ε values. With VRs of 63 % and higher, these waveform fits are of good quality. Event 113 (ML2.5) occurred in the hours following the shut-down of the Basel project. The Hudson plot for this event shows a good agreement between full, CDC and NSS solutions (Fig. 10), which confirms the large isotropic component (i.e., 31 % compared to 46 % DC, Table 4). This supports the idea of a tensile mechanism superimposed on shear motion during the rupture. Events 82 and 94 (i.e., the other two events with F-test significance values above 85 %) also suggest superimposed shear and tensile faulting because the full, CDC, and NSS solutions determine a similar source type (Fig. 10). For these events the CDC model yields a volumetric increase of the source region of 1–10 m3 [using Eq. 1 of Müller (2001) and a bulk modulus of 3e12 dyne/cm2]. In contrast, for events 5, 147 and 162, the CDC mechanism reproduces neither the full nor the NSS solution, each of which have negative κ values. The negative κ would explain a different rupture process to the one found for events 82, 94, and 113. Instead of a composite rupture with crack opening, negative κ suggests crack closing. The mechanisms obtained from full moment tensor inversions and the NSS approach for events 5, 147, and 162 evoke double-couple mechanisms associated with volumetric contractions. Even though the CDC search allows for negative crack components, the favored CDC results indicate no closing mechanism that would explain the negative κ values of the full moment tensor inversions (Fig. 10). This suggests that volumetric contractions may be associated with more complicated processes than a simple closing of parallel fracture planes during shear motion (CDC model).
Hudson representations of the moment tensor (MT) solutions of the six earthquakes with more than 15 % absolute isotropic components in the full moment tensor inversion (square NSS, circle CDC model, triangle full MT). The colored contours in the Hudson diagram are normalized relative to the best VR obtained in the NSS and show the top 5 percentiles for each event. These NSS distributions of the largest fits are rather extended but their best solutions are in general good agreement with the full moment tensor results. For Event 113, the top 5 percentile tends to indicate a region located between a DC source and a positive crack source as found with the other techniques
3.3 Temporal and spatial patterns of isotropic components
The largest isotropic components in the full moment tensor inversions are found early in the induced earthquake sequence during periods of fluid injection or shut-in (Fig. 11; Table 1). This influence of injected fluids on earthquake source mechanisms diminishes in the following months when fluids likely diffuse and source mechanisms return to purely tectonic shear dislocations. The isotropic components fall below 10 % and for the last six events the solutions are centered on the double-couple mechanism (Fig. 7). The ML1.7+ earthquakes with the largest isotropic components as determined in the full moment tensor inversions are distributed between the injection point and about 400 m SSE of it (Fig. 1). Outside of this region (i.e., for along-profile coordinates of <−0.2 and >0.2 km in Fig. 1c) the events have lower volumetric components. The spatial transitions from regions of low to high isotropic components are sudden. Although the events 102 and 167 are located immediately east of event 113 (pISO = 31 %) their full moment tensor inversions determine only 3 % isotropic component. This sharp transition suggests that fluids migrated south from the injection point, and were trapped by steep barriers of hydraulic potential and/or low permeability. Indeed, the double-couple events that occurred in the post-injection phase locate further away from the injection well, beyond these barriers. This is consistent with the observation that these latest events were remotely triggered by positive Coulomb stress changes and not by induced pore pressure changes (Catalli et al. 2013). At this point we stress that the observation of near-double-couple events just beyond both ends of the zone characterized by elevated isotropic components (Fig. 1) argues against spurious effects of an inaccurate velocity model. Indeed, if heterogeneities not captured in the velocity model were the causes of elevated isotropic components, they would also affect the near-double-couple events because their waves propagate through much of the same volume.
Time evolution of the earthquake source parameters. a Variation of the absolute isotropic component found for the 28 earthquakes between December 2006 and May 2007. b Moment magnitude vs time. The dots are color-coded by the corresponding isotropic component. No evidence of magnitude dependence of the isotropic changes is observed. c Temporal change of the downhole pressure in kPa (red) measured at the injection site and of the injection flow rate (l/min) compared to earthquake’s occurrence. Dot color gives the absolute isotropic component (colorscale in b), and dot size is proportional to ML
The influence of the fluid injection and migration is further suggested by the volumetric parameter κ. When limiting the observation to the six earthquakes with more than 15 % isotropic component, one can notice that during the injection periods events 82, 94, and 113 have positive κ and deviate systematically from the double-couple mechanism in the three approaches considered in this study (Fig. 10). Positive κ indicates volumetric expansion that is likely to result from the high injection rate and/or pore pressure occurring at the same time period (Fig. 11). However, after the shut-down of the project when fluids are no longer injected into the reservoir, the newly opened cracks tend to close. Such mechanism would trigger a volumetric contraction of some sections of the reservoir that were the most reactive during the injection period. With the exception of event 5 that is the first earthquake of the studied Basel sequence, events 147 and 162 with negative κ occurred within the days following the shut-down. Given their close proximity (about 100 m) to the well injection site, and to event 113 that shows the largest isotropic component of the sequence, they likely correspond to a reaction to the fluid pressure drop at depth. The earthquakes following later on show clear double-couple mechanisms in all inversions (Figs. 7, 11). Figure 11c further suggests strong links between fluid injection and isotropic components measured through the moment tensor inversions. The color gradient shows the decrease in the isotropic components from events 82 to 112 at the time the fluid injection rate dramatically drops during the shut-in and active venting periods. This temporal effect is in agreement with the loss of fluid pressure at depth. As a result, the system grows less susceptible to tensile faulting as the differential stress increases back to its pre-injection level.
We acknowledge that the observed spatial and temporal patterns of isotropic moment are based on inversions, which do not exceed the statistical 95 % confidence threshold. Nevertheless, we find it unlikely that the described relationships are a result of coincidence. This would imply that numerical artifacts in the inversion happened to amplify the isotropic component near times of fluid injection while leaving later events unaltered. Moreover, the sharp transition between the pISO = 31 % of event 113 and other events immediately to the south with pISO = 3 % may hardly result from differences in the source-receiver geometry because moment tensors were calculated with the same set of five strong-motion stations. Only 6 out of the 28 M2+ earthquakes (Table 1) were inverted with less than 5 stations, but do not exhibit unusually elevated isotropic components except for event 147. In addition, most of the events happened in the 2006–2007 winter season. No change in noise conditions, including anthropogenic source, is expected since the injection site is in the city of Basel.
Finally, we did not find a clear relationship between earthquake magnitudes and their isotropic components (Fig. 11b). Fifteen events have Mw lower than the average magnitude of 2.37. Only six of them have an isotropic component larger than 10 %, including four earthquakes with more than 15 % isotropic part (Table 4). Except for one of these four events that has the lowest reported Mw, their moment tensor solutions are of satisfying quality with VR larger than 65 %. We note that events 113 and 94 having 31 and 17 % positive isotropic components, respectively, have Mw larger than 2.4. This argues against elevated background noise as the source of spurious isotropic components.
3.4 Comparison with previous studies
Our findings support the results of Zhao et al. (2014) who found an increased number of volumetric sources during and immediately after the fluid injection at the Basel geothermal site. Considering the differences in the methods and datasets between the two studies, such general agreement bolsters spatio-temporal variations in compound sources due to fluid injection, even though exact values of the estimated ISO percentages may differ (Fig. 8). Nevertheless, our results differ from those of the study of Zhao et al. (2014) with respect to the significance of the full solutions compared to constrained solutions. According to the Zhao et al. (2014) study, all the 19 M2+ earthquakes passed the 95 % confidence threshold of the F-test statistics between their double-couple solutions and their full moment tensor solutions. To our mind, their finding is inconsistent with a return to pure double-couple mechanisms in the later Basel sequence. The different numbers of unknowns in the inversions schemes could explain part of the discrepancies. Whereas Zhao et al. (2014) compare the full moment tensor inversions to constrained pure double-couple inversions, our study relaxes this constraint by including a CLVD component and thus another degree of freedom. While we believe that including the CLVD mechanism is appropriate for fluid-induced earthquakes, we find it unlikely that removal of this extra degree of freedom directly results in the high significance levels found in Zhao et al. (2014).
Even though we find that only one event passes the null hypothesis condition between deviatoric and full moment tensor solutions, a total of six events have F-test confidence levels above 75 %, including three above 85 % (Table 4). For these last three earthquakes, there is by definition more than an 85 % probability that the full solutions are significant compared to the deviatoric solutions. Figure 8 also shows that the majority of isotropic components found in our study and that of Zhao et al. (2014) agree within ±5 %, both in terms of signs and amplitudes. We note that on average, we measure a smaller isotropic component. Also, the largest discrepancies between the two studies are found for events with the smallest volumetric changes (i.e., between −10 and 10 %) that have the lowest F-test confidence levels. On the other hand, the largest isotropic component events show agreement between the two independent analyses, and are also associated with the largest F-test confidence values (Fig. 8).
3.5 Disagreement with first-motion polarities
Although shear fault plane orientations of our moment tensor inversions agree well with those determined from first-motions (Deichmann and Ernst 2009; Deichmann et al. 2014), nearly all inverted mechanisms predict P-wave polarities, which contradict at least one observed first-motion polarity (Figs. 6, 7). This disagreement was also observed in the study of Zhao et al. (2014) and may, in part, be the result of low SNR first-P waveforms and of an inaccurate velocity model. Uncertainties in event depths, which may particularly affect polarity studies (Deichmann and Ernst 2009; Deichmann et al. 2014), are likely of secondary importance, because we adopted the same locations (latitude, longitude, and depth) used in the focal mechanism study of Deichmann and Ernst (2009). We refrain from a detailed comparison between waveform and polarity inversions because the reliability of binary polarity information is difficult to assess, especially in the presence of low signal-to-noise ratio and emerging P waves. Although likely stabilizing source inversions, combination of first-motion information with full waveform inversions presents an on-going challenge, because a physically based weighting of the two data types has yet to be established (Guilhem et al. 2014).
Another reason for the disagreement between our inverted moment tensors and first-motion polarities may be found in complex source effects, for which our constrained inversion schemes cannot fully account. In case of the CDC moment tensor this means that a superimposed shear and tensile fault with common fault planes incompletely explains the actual source mechanisms. More generally, the shear and tensile components may each have their own fault plane orientations (Julian et al. 1998). Wing fractures form an important special case in which tensile fault plane orientation depends on pre-existing principal stresses rather than on shear plane orientation (Vavryčuk 2011; Johnson 2014b). This fault model accounts for laboratory observations that shear faults extend themselves by growing tensile fractures at their ends (Griffith et al. 2009; Misra et al. 2009). At this point the applicability of the wing fracture model to our induced earthquake data set is purely speculative. However, it is interesting to note that the wing fracture model predicts a higher corner frequency for the isotropic component than for the shear component (Johnson 2014b). Consequently, if part of the P-wave radiation is due to the isotropic component of the tensile wing cracks, P-waves should have smaller amplitudes at lower frequencies. This agrees with the seismograms in Fig. 2, which show a dominant P-wave in the unfiltered time series, and a substantially weaker P-wave in the 0.5–3.0 Hz range. It remains to be shown if a moment tensor constraint accounting for wing cracks would indeed improve agreement with first-motion polarities. This may be complicated by magnitude-dependent time delays between P-wave radiation of the shear and tensile components (Johnson 2014b). Moreover, investigating the wing crack model would require waveform inversions at higher frequencies. This is beyond the capabilities of the 1D velocity model used in the study, which does not fully capture the complexity of the local and regional tectonic settings. In any case, a confirmation of the wing crack model would provide a physical model for temporal changes in the fluid diffusivity during geothermal reservoir enhancement.
4 Summary and conclusions
Our full, constrained and stochastic moment tensor inversions successfully model S-wave dominated filtered waveforms of all the M1.7+ induced Basel earthquakes. The source mechanisms suggest that injected fluids were capable of opening up 1–10 m3 of new void spaces during individual earthquakes via some degree of tensile fracturing superimposed on shear failure. Accordingly, fluid injection increased pore pressure enough that the Mohr circle touched the Griffith failure envelope at negative normal stresses (Fischer and Guest, 2011). In more technical terms, the specific findings of our study can be summarized as follows:
-
1.
The inverted isotropic component of only one event (event 113) is statistically significant as indicated by F-tests of full and deviatoric moment tensors.
-
2.
The isotropic components of the remaining events still show temporal and spatial patterns, which reflect a reasonable response to fluid injection and which are difficult to explain with inaccurate seismic velocity models or mere coincidence.
-
3.
Our inverted moment tensors show disagreement with some of the first-motion polarities. We suggest that this may indicate unaccounted source effects, such as wing crack formation, if reported polarities are not due to velocity model approximation and/or low signal to noise ratio.
While our approach in this multi-step analysis differs from the inversions computed by Zhao et al. (2014), our findings generally agree. As a result, these two independent studies bolster the idea of volumetric faulting during the 2007 fluid stimulation of the Basel geothermal area.
Findings 2 and 3 had previously been noted by Zhao et al. (2014). However, compared to a pure shear mechanism, these authors found that all the 19 M2+ earthquakes had F-test significance levels above the 95 % threshold, and concluded that for all events the full moment tensor inversion provides significantly better results than the double-couple inversion. This is in disagreement with our Finding 1 and with the temporal decrease of the rate of compound sources noticed in both studies. We argue that our deviatoric inversion scheme may be more relevant to the present data set, because it allows for shear faulting in addition to a CLVD mechanism, which can represent the opening of fractures compensated by a volumetric decrease, e.g., due to fluid flow (Kanamori et al. 1993; Konstantinou et al. 2003; Tkalčić et al. 2009). For a tensile crack undergoing an overall volumetric change, the CLVD furthermore constitutes the deviatoric component responsible for S-wave radiation (Walter et al. 2009). In other words, statistical testing is contingent upon the accuracy of the theoretical source models. In fact, in our case the 95 % confidence threshold may be too conservative, because it renders almost all of our isotropic components insignificant, even though they show a clear spatial and temporal relationship to fluid induction.
In general, the finding of isotropic moment tensor components of the Basel events agrees with other seismological investigations of geothermal fields around the world (Ross et al. 1996; Cuenot et al. 2006; Sileny et al. 2009; Guilhem et al. 2014). Nevertheless, evaluating the physical significance of isotropic moment tensor components remains a challenge. It could be tackled with supplementary types of data, such as borehole seismometer records enhancing coverage of the focal sphere. Moreover, other source models going beyond our superimposed shear and tensile mechanism may be needed. For instance, the wing crack model (Johnson 2014b) may stabilize inversions to improve agreement with first-motion polarities.
Growing data volumes of induced earthquakes will promote detailed future studies of these events with the goal of further investigating the role of volumetric fracturing during reservoir stimulation. At this point, the results for Basel from this present study support the occurrence of volumetric faulting previously reported by Zhao et al. (2014), and suggest that our approach could provide valuable information about the efficiency of reservoir stimulation. While challenging, reducing numerical uncertainties of seismic source inversions could therefore enhance seismological monitoring tools and lead to improvements in reservoir management.
References
Baer, M., Deichmann, N., Braunmiller, J., Clinton, J., Husen, S., Faeh, D., et al. (2007). Earthquakes in Switzerland and surrounding regions during 2006. Swiss Journal of Geosciences, 100, 517–528.
Ben-Zion, Y., & Ampuero, J. P. (2009). Seismic radiation from regions sustaining material damage. Geophysical Journal International, 178(3), 1351–1356.
Bowers, D., & Hudson, J. A. (1999). Defining the scalar moment of a seismic source with a general moment tensor. Bulletin of the Seismological Society of America, 89(5), 1390–1394.
Catalli, F., Meier, M.-A., & Wiemer, S. (2013). The role of Coulomb stress changes for injection-induced seismicity: the Basel enhanced geothermal system. Geophysical Research Letters,. doi:10.1029/2012GL054147.
Cuenot, N., Charléty, J., Dorbath, L., & Haessler, H. (2006). Faulting mechanisms and stress regime at the European HDR site of Soultz-sous-Forêts, France. Geothermics, 35(561–575), 2006. doi:10.1016/j.geothermics.11.007.
Deichmann, N., & Ernst, J. (2009). Earthquake focal mechanisms of the induced seismicity in 2006 and 2007 below Basel (Switzerland). Swiss Journal of Geosciences, 102, 457–466. doi:10.1007/s00015-009-1336-y.
Deichmann, N., & Giardini, D. (2009). Earthquakes induced by the stimulation of an enhanced geothermal system below Basel (Switzerland). Seismological Research Letters, 80, 5. doi:10.1785/gssrl.80.5.784.
Deichmann, N., Kraft, T., & Evans, K. F. (2014). Identification of faults activated during the stimulation of the Basel geothermal project from cluster analysis and focal mechanisms of the larger magnitude events. Geothermics,. doi:10.1016/j.geothermics.2014.04.001. (in press).
Dreger, D. S. (2003). TDMT_INV: time domain seismic moment tensor INVersion. International Handbookof Earthquake and Engineering Seismology, 81B, 1627.
Fischer, T., & Guest, A. (2011). Shear and tensile earthquakes caused by fluid injection. Geophysical Research Letters, 38, 5.
Ford, S. R., Dreger, D. S., & Walter, W. R. (2009a). Network sensitivity solutions for regional moment-tensor inversions. Bulletin of Seismological Society of America, 100(5A), 1962–1970. doi:10.1785/0120090140.
Ford, S. R., Dreger, D. S., & Walter, W. R. (2009b). Identifying isotropic events using a regional moment tensor inversion. Journal of Geophysical Research Solid Earth, 114, B1. doi:10.1029/2008JB005743.
Goertz-Allmann, B. P., Edwards, B., Betmann, F., Deichmann, N., Clinton, J., Fäh, D., & Giardini, D. (2011). A new empirical magnitude scaling relation for Switzerland. Bulletin of Seismological Society of America, 101(6), 3088–3095. doi:10.1785/0120100291.
Griffith, W. A., Sanz, P. F., & Pollard, D. D. (2009). Influence of outcrop scale fractures on the effective stiffness of fault damage zone rocks. Pure and Applied Geophysics,. doi:10.1007/s00024-009-0519-9.
Guilhem, A., Hutchings, L. J., Dreger, D. S., & Johnson, L. (2014). Moment tensor inversions of the ~M3 earthquakes in the Geysers Geothermal Fields, California. Journal of Geophysical Research, 119(3), 2121–2137. doi:10.1002/2013JB010271.
Hudson, J. A., Pearce, R. G., & Rogers, R. M. (1989). Source type plot for inversion of the moment tensor. Journal of Geophysical Research, 94(B1), 765–774.
Johnson, L. (2014a). Source mechanisms of induced earthquakes at the Geysers Geothermal Field. Pure and Applied Geophysics,. doi:10.1007/s00024-014-0795-x.
Johnson, L. (2014b). A source model for induced earthquakes in the Geysers geothermal reservoir. Pure and Applied Geophysics,. doi:10.1007/s00024-014-0798-7.
Jost, M. L., & Herrmann, R. H. (1989). A student’s guide to and review of moment tensors. Seismological Research Letters, 60, 37–57.
Julian, B. R., Miller, A. D., & Foulger, G. R. (1998). Non-double-couple earthquakes I. Theory. Reviews of Geophysics, 36, 525–549.
Kanamori, H., Ekström, G., Dziewonski, A., Barker, J. S., & Sipkin, S. A. (1993). Seismic radiation by magma injection: an anomalous seismic event near Tori Shima, Japan. Journal of Geophysical Research, 98(B4), 6511–6522.
Kawakatsu, H. (1991). Insignificant isotropic component in the moment tensor of deep earthquakes. Nature, 351, 50–53. doi:10.1038/351050a0.
Konstantinou, K. I., Kao, H., Lin, C. H., & Liang, W.-T. (2003). Analysis of broad-band regional waveforms of the 1996 September 29 earthquake at Bárdarbunga volcano, central Iceland: investigation of the magma injection hypothesis. Geophysical Journal International, 154, 134–145.
Minson, S., & Dreger, D. (2008). Stable inversions for complete moment tensors. Geophysical Journal International, 174, 585–592.
Minson, S. E., Dreger, D. S., Bürgmann, R., & Kanamori, H. (2007). Seismically and geodetically determined nondouble-couple source mechanisms from the 2000 Miyakejima volcanic earthquake swarm. Journal of Geophysical Research, 112, B10308. doi:10.1029/2006JB004847.
Misra, S., Mandal, N., Dhar, R., & Chakraborti, C. (2009). Mechanisms of deformation localization at the tips of shear fractures: findings from analogue experiments and field evidence. Journal of Geophysical Research, 114, B04204. doi:10.1029/2008JB005737.
Müller, G. (2001). Volume change of seismic sources from moment tensors. Bulletin of the Seismological Society of America, 91, 880–884.
Ripperger, J., Kästli, P., Fäh, D., & Giardini, D. (2009). Ground motion and macroseismic intensities of the seismic event related to geothermal reservoir stimulation below the city of Basel—observations and modeling. Geophysical Journal International, 179, 1757–1771. doi:10.1111/j.1365-246X.2009.04374.x.
Ross, A., Foulger, G. R., & Julian, B. R. (1996). Non-double-couple earthquake mechanisms at the Geysers geothermal area, California. Geophysical Research Letters, 23(8), 877–880.
Rössler, D., Krüger, F., & Rümpker, G. (2007). Retrieval of moment tensors due to dislocation point sources in anisotropic media using standard techniques. Geophysical Journal International, 169, 136–148. doi:10.1111/j.1365-246X.2006.03243.x.
Saikia, C. K. (1994). Modified frequency-wavenumber algorithm for regional seismograms using Filon’s quadrature: modeling of L g waves in eastern North America. Geophysical Journal International, 118, 142–158. doi:10.1111/j.1365-246X.1994.tb04680.x.
Scognamiglio, L., Tinti, E., & Michelini, A. (2009). Real-time determination of seismic moment tensor for the Italian region. Bulletin of the Seismological Society of America, 99, 2223–2242. doi:10.1785/0120080104.
Sileny, J., Hill, D. P., Eisner, L., & Cornet, F. H. (2009). Non-double-couple mechanisms of microearthquakes induced by hydraulic fracturing. Journal of Geophysical Research, 114, B08307. doi:10.1029/2008JB005987.
Tape, W., & Tape, C. (2012). A geometric setting for moment tensors. Geophysical Journal International, 190, 476–498. doi:10.1111/j.1365-246X.2012.05491.x.
Templeton, D. C., & Dreger, D. S. (2006). Non-double-couple earthquakes in the Long Valley Volcanic region. Bulletin of the Seismological Society of America, 96(1), 69–79. doi:10.1785/0120040206.
Tkalčić, H., Dreger, D. S., Foulger, G. R., & Julian, B. R. (2009). The puzzle of the 1996 Bárdarbunga, Iceland, earthquake: no volumetric component in the source mechanism. Bulletin of the Seismological Society of America, 99(5), 3077–3085.
Vavryčuk, V. (2001). Inversion for parameters of tensile earthquakes. Journal of Geophysical Research: Solid Earth, 106(B8), 16339–16355.
Vavryčuk, V. (2011). Detection of high-frequency tensile vibrations of a fault during shear rupturing: observations from the 2008 West Bohemia swarm. Geophysical Journal International, 186(3), 1404–1414.
Walter, F., Clinton, J. F., Deichman, N., Dreger, D. S., Minson, S. E., & Funk, M. (2009). Moment tensor inversions of icequakes on Gornergletscher, Switzerland. Bulletin of Seismological Society of America, 99(2A), 852–870.
Wang, C. Y., & Herrmann, R. B. (1980). A numerical study of P-, SV-, and SH-wave generation in a plane layered medium. Bulletin of Seismological Society of America, 70, 1015–1036.
Zhao, P., Oye, V., Kühn, D., & Cesca, S. (2014). Evidence for tensile faulting deduced from full waveform moment tensor inversion during the stimulation in the Basel enhanced geothermal system. Geothermics. doi:10.1016/j.geothermics.2014.01.003 (in press).
Acknowledgments
We thank Nicholas Deichmann, Stephan Husen, Toni Kraft, Daniela Kühn and Peng Zhao for refined event relocations and fruitful discussions. Part of this work constitutes a contribution to projects GEOTHERM2 and GEISER. FW was partially funded by the European Union Seventh Framework Programme (FP7-PEOPLE-2011-IEF) under Grant agreement no. 29919.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editorial handling: S. M. Schmid.
Rights and permissions
About this article
Cite this article
Guilhem, A., Walter, F. Full, constrained and stochastic source inversions support evidence for volumetric changes during the Basel earthquake sequence. Swiss J Geosci 108, 361–377 (2015). https://doi.org/10.1007/s00015-015-0197-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00015-015-0197-9